随机干扰下拓扑时变Kuramoto网络事件触发固定时间同步
孙 佳,贾玉斌,武永宝,董 璐,刘 剑
(1.东南大学自动化学院,江苏 南京 210096;2.东南大学网络空间安全学院,江苏 南京 210096)
1 引言
复杂网络作为一种描述自然界和人类社会中存在的种种联系和相互作用的数学模型,在自然科学、控制理论、社会学等各个领域都存在着广泛应用[1–2].在已有的复杂网络模型中,Kuramoto 型振子网络(又称Kuramoto 网络)是指一种耦合相振子模型,其基本思想是将复杂网络建模为多个相互耦合的振子系统[3–4].利用该模型来刻画和研究复杂网络系统的动力学特性具有良好的便利性,因而其被广泛应用于多种耦合动态场景的研究中[5–6].在系统科学和控制工程研究领域,利用代数图论和微分方程理论可以严格地分析振子网络耦合条件对网络性质的影响.于是,Kuramoto型振子网络同步控制领域在这一思路下产生了丰富的理论成果[7–8].在不考虑随机干扰影响的情况下,研究人员从考虑网络拓扑影响方面和网络振子节点动力学特征等方面入手[9–11],对耦合振子网络的同步进行了深入而广泛的研究[12–14].然而在实际情况中,振子耦合状态大概率是变化的,随机噪声可能存在于复杂网络的耦合通道及信号传输通道中.在现有针对噪声影响的研究中,一般在振子动力学方程中添加高斯白噪声项来进行建模,并采用平均场的方法对其同步特性进行研究,利用统计学的方法获得定性的结论[15–16].另外,最近Wu和Li[17]采用分层分布式的控制结构,对耦合网络和通信信道中可能存在随机干扰的Kuramoto型振子网络讨论全局相位和频率同步的控制方案.
另外,研究耦合振子网络相位同步调节速率的影响因素也是十分重要的问题.目前多数相关文献都是推导出渐进同步或者是指数同步的条件[14,18–19]以增加调节速率.这些成果中均存在调节时间会受初始状态影响的局限,而固定时间稳定性理论能够解决这一问题.例如,Wu和Li[20]利用多层结构的分布式控制方式,针对Kuramoto型振子网络的相位同步和频率同步问题给出了有限时间和固定时间的解决方案,并在随后的研究中进一步改进控制器的形式,减少了实现固定时间控制时控制信号的抖振现象[21].
为了提高Kuramoto型振子网络同步控制的鲁棒性,如何放宽对初始条件和网络通信的要求,同时设计具有抗干扰能力的控制策略成为了一个重要的研究方向.具体来说,对Kuramoto型振子网络的同步控制通常需要更强的鲁棒性和分布式的控制结构[9].然而目前研究成果多侧重考虑提升鲁棒性,但从分布式结构的角度进行优化的结果还较欠缺.分布式的网络化控制必须要考虑计算及监测资源的有限性和网络通道的拥塞.目前在复杂网络系统控制领域,解决此类问题的主要手段就是引入事件触发机制[22–26],且当复杂网络中存在随机干扰时,也会给事件触发条件的设计和Zeno行为的分析带来一些技术上的难度,因此目前该方向的结果还比较少[27–29].目前已有的类似结果对于解决Kuramoto网络的同步问题大多不能提供更直接的方法指引,且对于拓扑变化的耦合振子网络的情况还没有相应的结果.笔者在前期工作[30–31]中引入了事件触发机制,优化了控制动态表现且降低了网络通信资源的占用,但是没有充分考虑耦合通道中存在随机干扰对网络同步控制性能的影响,以及随机干扰对Zeno行为的理论分析的影响,而目前针对Kuramoto网络同步的文献中,仍欠缺能够综合抵抗耦合中的随机干扰、事件触发机制下固定时间内完成同步、适应切换的网络拓扑这3个需求的结果.
综合考虑目前的相关结果和存在的问题,本文针对耦合网络中存在随机干扰的Kuramoto型振子网络,引入事件触发的分布式控制机制,降低计算资源和通信资源的占用.同时,采用具有不同拓扑的多层分布式控制网络结构,适应切换的拓扑,并对随机干扰具有一定的鲁棒性.本文主要贡献总结为:
1)在事件触发机制下,针对Kuramoto型振子网络设计了具有不同拓扑的多层分布式控制结构.相比于笔者的前期工作(文献[30]),其控制网络各层可以设置不同的连通度.本文中,同步收敛的调节速率不会受较弱的耦合强度及未知的初始节点状态影响和耦合网络拓扑变换影响.
2)对耦合网络中可能存在的随机干扰项进行了合理的建模,借助随机微分方程理论和固定时间事件触发控制给出了新的控制方案,相比于文献[30]的多层网络结构,本文所提出的控制方案额外增加了用于抵消随机干扰的控制层,增强了鲁棒性.
3)相比于现有的Kuramoto 型振子网络同步控制的结果,如文献[17,20–21],本文综合考虑了随机干扰、耦合网络拓扑变化的影响,以及同步误差收敛的速度,并利用事件触发机制减少了计算和通信资源的占用.对Zeno行为进行了理论分析,根据改进的测量误差重新设计了Lyapunov函数,使用Itˆo公式和Kuramoto网络的耦合动态特性,经不等式放缩之后得出相邻触发时刻间隔的下界.
符号说明:1N为维度为N的全1向量,Y X为矩阵,Y的X幂次矩阵,LYX表示图G(Y X)的Laplacian矩阵,XT为矩阵或者向量X的转置,λ2(·)和λN(·)分别为矩阵的第二最小特征值和最大特征值,E(·)为变量的期望,tr{·}表对矩阵求迹,sgn(·)为符号函数,tanh(·)为双曲正切函数.
2 预备知识
2.1 代数图论
2.2 问题阐述
为了便于描述,此处给出随机Kuramoto型振子网络的同步控制模型.本文主要考虑来自振子耦合通道中产生的随机干扰,所研究的Kuramoto型随机振子网络模型如下:
其中: 集合Θ表示整个圆周上的相位角;振子的相位θi ∈Θ;K >0表示耦合强度系数;N为网络中的振子节点总数;ωi ∈R表示振子i的自然频率或固有频率,并且满足|ωi|≤,其中是已知正常数;aij(t)表明耦合拓扑是时变的,其变化特性将在随后的假设条件1中给出解释.针对每个振子节点设计一个控制器,这些控制器构成一个分布式控制网络,将控制网络称为控制层,耦合振子网络称为振子层.本文考虑来自于振子层的随机干扰,以上模型中的随机项Wi(t)具有如下形式:
其中:ζ表示噪声的强度系数;pij表示耦合网络通道的噪声强度矩阵P中的元素,且P的Laplacian矩阵用LP表示.当且仅当aij(t)>0时,有pij>0,反之pij=0,即通常噪声强度矩阵P对应的拓扑图与耦合振子网络的拓扑图相同.由于同一个耦合通道内的噪声强度相同,所以P具有对称性.在本文中,认为在所有的耦合通道中噪声在节点处对振子的动态起作用,整个耦合网络环境内噪声来源和形式相似.此处建模设定可以参考文献[17]及文献[23];w(t)为定义于具有自然滤子{Ft}t≥t0的完备概率空间(Ω,F,P)上的一维标准布朗运动(或称维纳过程).根据随机干扰的耦合振子网络模型(1),本文拟对其设计分布式控制器,以实现其固定时间相位同步控制.
参考文献[32–33],本文对所研究的耦合振子网络具有的拓扑变化特性做以下假设.
假设1耦合振子网络连接的图会在一个有限集合S={G1,G2,···,Gn}中变化,这一集合包含了所有耦合振子网络可能出现的连接拓扑图,并且集合内的图均是无向连通图.
为了便于描述连接拓扑图的变化时序及切换时间,定义ˆN={1,2,···,n}是一个图集合的标记集合.同时定义一个切换信号η(t)=[0,∞)→ˆN.于是,Kuramoto 型耦合振子网络的连接拓扑即可以用Gη(t)(η(t)∈,Gη(t)∈S)描述,其拉普拉斯矩阵和邻接矩阵分别表示为Lη(t)和Aη(t).
假设2在整个拓扑变化的过程中,噪声强度连接构成连通图,且对应的Laplacian矩阵LP的最大特征值存在上界.
2.3 定义及引理
定义1文献[17]带有随机干扰项的Kuramoto型振子网络模型(1),对于分布式控制输入ui(t)和给定任意振子节点相位初始状态θi(0)都可得一个与初始状态无关的常数Tmax,满足期望调节时间E(T)≤Tmax,且=1,其 中i,j=1,···,N,则定义耦合振子网络能够以概率1全局固定时间相位同步,Tmax则为最大全局相位同步调节时间.
定义2带有随机干扰项的Kuramoto型振子网络模型(1),对于分布式控制输入ui(t)和任意节点相位初始状态θi(0)都可得一个与初始状态无关的常数Tmax,满足期望调节时间E(T)≤Tmax,且|θi(t)-θj(t)|≤e}=1,其中i,j=1,···,N,e为一预设充分小的正常数.则定义耦合振子网络能够以概率1全局实际固定时间相位同步,Tmax则为最大全局相位同步调节时间.
引 理2[35]对任意一实值变量x ∈R,都 有0 ≤|x|-xtanh(γx)≤,其中γ ≫1,且ι=0.2785是一个常数.
引理3[36]考虑一N维随机微分方程,dx(t)=f(x(t),t)dt+g(x(t),t)dB(t),t≥t0,其中x ∈RN表示N维状态向量,其初始值为x(t0).同时f:RN →RN以及g:RN →RN×M为连续函数,并满足f(0)=0,g(0)=0.B(t)=[b1··· bM]为M维标准布朗运动(或称维纳过程),˙B(t)对应为M维独立高斯白噪声,并且对连续二次可微的径向无界非负函数V(x):RN →R+,根据Itˆo 公式可得到其扩散算子LV有如下形式:
引理4[37]如果存在一个连续二次可微的径向无界非负函数V:RN →R+,并且对于任意x ∈RN,算子LV(x)都有
那么可以称闭环系统能够依概率固定时间稳定,其中:a>0,b>0,0<α<1,β >1均为常数,并且有全局固定时间收敛调节时间T满足E(T)≤1/(a(1-a))+1/(b(β-1)),此处E(T)是一个随机变量,并且满足满足E(T)∈(0,+∞).
3 主要结果
本文设计了一种具有分层结构的耦合振子同步控制网络,构建的控制网络包含3 层结构,这3层控制网络节点连接的拓扑图分别记为G(B),G(C)和G(R),这3个图均需要设计为连通图.每个网络振子节点都有自己的一组非周期控制序列,其控制信号值在自己的事件触发时刻完成计算和更新,三层控制网的触发时刻不作区分.如振子i的触发时刻标记为,···}.本文将振子节点互连构成的真实网络称为耦合网络.振子i的分布式控制器的具体形式为
事件触发判别函数定义为
其中δ ∈(0,1)为事件触发参数,可以根据实际需要选取.事件触发判断函数(7)表明,振子i需要监测|εi(t)|的值,当gi(t)≥0时,振子i的控制器触发并更新控制信号.根据gi(t),可以获得下一个触发时刻,即
定理1∀K>0,∀θi(0)∈Θ,在具有满足假设1条件的时变无向连通图Gη(t)耦合作用下,针对含有满足假设2随机干扰的Kuramoto模型振子网络(1),若使用事件触发分布式控制器(5)及事件触发判别函数(8),且选取各参数及控制网络的连通度满足如下条件:
选取如下Lyapunov函数为V=,借助随机微分方程理论中的微分算子L对其作用可得
因此,结合文章中所给出的参数条件,以及控制信号与测量误差的代数关系,可得
考虑到平均相位误差ei(t)=θi(t)-(t),得到θi(t)-θj(t)=ei(t)-ej(t).同时,考虑到本文中讨论的无向连接拓扑图的Laplacian矩阵具有对称性,得
当|ej(t)-ei(t)|>0时,参考引理1,式(14)可变为
对于函数sin(·)/(·),其取值范围为[cosϕ,1),其中tanϕ=ϕ,且ϕ ∈±(π,2π),有
参考引理1有
选取满足定理1中条件的控制器参数,即可以实现
根据引理3,可以证明所设计的控制器可以使得整个振子网络在不受初始状态的影响下于指定时间内达到相位同步.期望调节时间的上界为
证毕.
注1定理1中所列出的控制器参数条件及控制网络连通度条件,均与耦合网络的具体拓扑无关.另外,在证明过程中可以发现,在已知噪声网络连通度上界的情况下,所设计的Lyapunov 函数形式也与耦合网络的拓扑变化无关.因此,本文所设计的分层式控制网络可以处理耦合网络拓扑时变时的相位同步控制问题.
注2相比于本文的前期工作(文献[30–31]),本文所提出的控制网络的各层,可以根据不同的需求选取不同的连通度.即本文控制器(5)中涉及的各网络邻接参数bij,cij,rij可以不同,而文献[30]中需要均与耦合振子网络中的aij相同.另外,随机干扰的存在并没有对最终固定时间同步的结果产生影响,鲁棒性增加.
注3根据定理1中提供的条件,控制网络各层包含固定时间调节、非线性项抵消、随机干扰抵消3个功能.根据式(18),越小的δ可以获得更快的同步调节速度.在某些特殊情况下(如有较大的耦合系数K),通过选取较小的δ来保证式(18)中的项前的系数为正数.较大的控制网络参数λ2(LR)和ρ3可以保证式(9)成立,并增强鲁棒性.
推论1针对耦合通道存在随机干扰的振子数为N的Kuramoto模型振子网络(1),其他参数假设条件及控制方法与1中相同,若其振子耦合拓扑图变化集合S中存在不连通图,则Kuramoto型振子网络(1)仍可以实现依概率相位实际固定时间同步.
证 若切换拓扑集合S中有存在不连通的拓扑图,由于邻接矩阵A和P仍具有对称性,则仍然能够得出邻接矩阵A和P相关的不等式
由于式(7)中使用的测量误差εi(t)中含有符号函数,因此在对事件触发条件进行Zeno行为分析的时候会产生奇异问题.因此用双曲正切函数代替εi(t)中的符号函数,以完成Zeno行为分析.参考引理2,可以得出LV≤-.其具体推导过程与定理1类似,因此省略.即使用双曲正切函数可以使Lyapunov 函数最终收敛至一个很小的0的邻域内,而不是完全收敛至0,实现实际固定时间同步,类似的处理方案和结果可以参考文献[25,38].由于参数γ ≫1 可调,因此,最终收敛邻域大小可以人为地根据实际需求进行调节.
在前期工作文献[30]中,针对Zeno行为进行分析时,由于不存在随机干扰,可以直接对事件触发条件中的测量误差的绝对值进行求导,再通过不等式放缩获得两次触发时间间隔的下界.而本文中针对测量误差函数进行数学代换,之后重新设计合适的Lyapunov函数,借助随机微分方程和Itˆo公式,在代入具有随机微分的各项后进行不等式放缩,最后推出两次触发时间间隔的下界.
定理2保持控制器(5)形式不变,选取替换双曲正切函数后的事件触发测量误差,并代入式(7)得到新的事件触发判别函数,可以保证Kuramo型耦合网络在实现实际固定时间相位同步的动态过程中不出现Zeno行为.
根据随机微分理论,具体有
依照上述定义,可以将hi(t)的微分表示为
测量误差可以表示为εi(t)=hi()-hi(t),随后针对测量误差设计Lyapunov函数
根据定理1中的分析及替换触发函数后收敛性的分析,Lyapunov函数V1的导数可以保证非负,可知网络相位同步误差是收敛的.因此对于tr(t)ψi(t)},可得
4 仿真分析
本节使用一个具有6节点的多层结构Kuramoto型振子网络控制系统,对所给出控制方案的有效性进行验证,耦合拓扑关系变化方式如下图1所示.
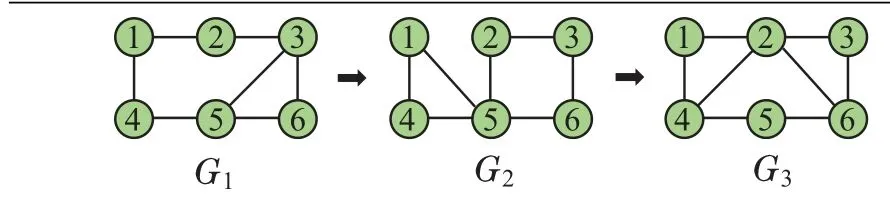
图1 振子耦合层网络拓扑变化示意图Fig.1 The network topology transformation of oscillator coupling layer
拓扑变化的图集合为S={G1,G2,G3};切换信号选取为η(t)={1,t∈[0,0.2);2,t∈[0.2,0.6);3,t ∈[0.6,+∞)}.G1,G2,G3的Laplacian矩阵分别用L1,L2,L3表示.
控制器结构包含3层网络,其拓扑结构对应的邻接矩阵分别记为R,B,C,与控制器(5)中描述对应.在下面的仿真中,选择其Laplacian 矩阵分别为L(B)=L3,L(C)=L2,L(R)=L1,于是可以得到λ2(LB)=0.8851,λN(LB)=2,λ2()=1.382,λ2(LR)=1,λ2()=1,控制器的相关参数选取为ρ1=2,ρ2=8,ρ3=0.1,µ=,δ=0.01,双曲正切函数中的参数γ=200.将以上参数代入定理1中的不等式进行验证,均满足条件.因此在控制器(5)的作用下,上述情况的耦合振子网络可以达到依概率相位固定时间实际同步,并计算出期望调节时间的上界为E(T)≤Tmax=5.911 s.具体仿真结果如图3–4所示.
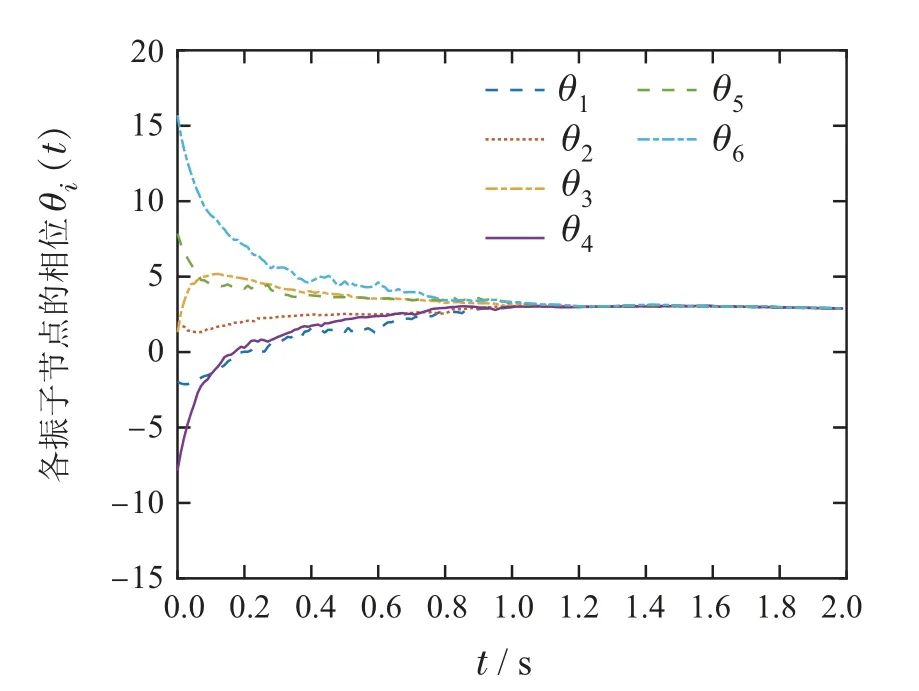
图3 各振子相位变化过程(噪声强度ζ=1)Fig.3 Phase of each oscillator(noise intensity ζ=1)
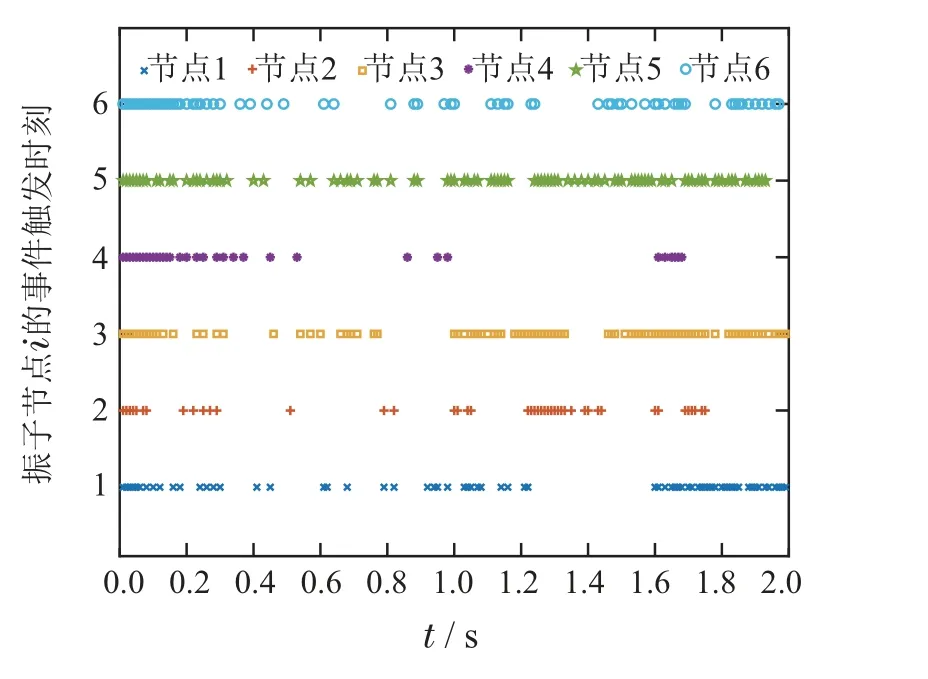
图4 各振子控制节点触发时刻(噪声强度ζ=1)Fig.4 Triggering time of each oscillator control node(noise intensity ζ=1)
由图3可知,各振子节点约在1.15 s达到实际相位同步,小于期望调节时间Tmax.振子网络的连接拓扑结构并不会影响整个网络的相位同步调节过程.另外可以观察到各振子的相位差收敛到一个很小的域内,故整个网络达到了依概率实际固定时间相位同步.
另外,为了说明本文提出的控制方案对Kuramoto型振子网络中存在的随机扰动具有一定的鲁棒性,在不改变耦合拓扑、初始状态和控制器参数的条件下,将噪声的耦合强度系数ζ改为2,仿真结果如图5–6所示.

图5 各振子相位变化过程图(噪声强度ζ=2)Fig.5 Phase of each oscillator(noise intensity ζ=2)
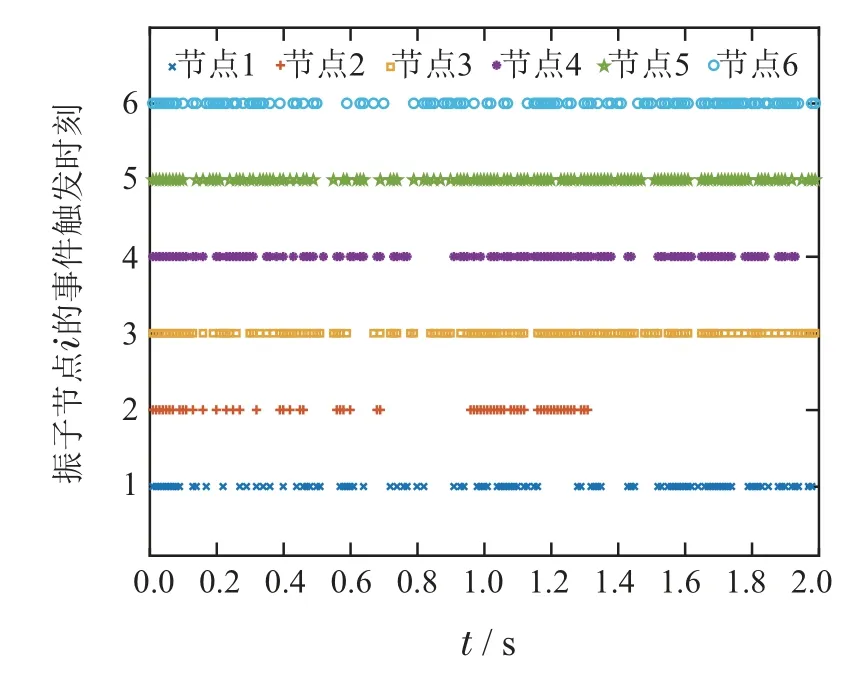
图6 各振子控制节点触发时刻图(噪声强度ζ=2)Fig.6 Triggering time of each oscillator control node(noise intensity ζ=2)
在增大噪声强度系数之后,Kuramoto型振子网络仍然可以保证在期望调节时间上界Tmax之内完成实际固定时间相位同步.尽管相位状态的波动情况更明显了以及触发次数增加了,但是仍然可以保证最终相位调节效果基本不变.在实际应用中,也可以通过调节参数γ来进一步缩小最终相位差.
5 结论
本文讨论了带有随机干扰的Kuramoto型振子网络的固定时间相位同步控制问题.首先,基于Kuramoto模型给出存在随机干扰的动力学方程,提出一种具有多层结构且各层拓扑不同的分布式控制方案.随后,引入事件触发机制,参考随机微分方程理论和固定时间稳定性理论,证明了所提出的方法可以使得耦合拓扑时变条件下的Kuramoto 振子网络完成相位固定时间同步.随后在触发条件中使用双曲正切函数代替符号函数,针对新的测量误差设计了Lyapunov函数,并证明所提出的事件触发控制方法能够避免Zeno现象的出现.最后,通过仿真算例验证了算法的有效性和鲁棒性.

