一种改进后的闭环解码算法
颜亚灵,王洛国,阎 瑞,武 明
(陆军防化学院,北京 102205)
双通道旋转变压器[1]作为伺服系统中的一种常用位置检测传感器[2],具有结构简单、精度高、可靠性强、耐高温、抗振动、防尘、耐油污、耐腐蚀、抗电磁干扰性强以及寿命长等优点,广泛应用于可靠性要求高且工况恶劣的高低、方向伺服系统角位置及角速度检测中。
自美国亚德诺半导体技术有限公司最先提出采用芯片解码将旋转变压器输出的电压信号转换为数字信号后,旋转变压器解码技术得到了快速发展,主要有硬件解码[3-4]、软件解码[5-6]和软硬融合解码[7]3种解码方式。硬件解码虽然体积小、结构简单以及程序相对固化,但存在不易修改、设计不灵活和解码精度差的问题。软件解码不需要使用专用的RDC(Resolver-to-Digital Converter)芯片,信号转换更加灵活方便,抗噪声效果强,可是计算过程较为复杂,可能产生滞后效应。软硬融合解码主要集中在对信号处理算法研究以及对应算法在集成芯片中的实现与应用上,既不易出错,又能灵活进行设计,得到了广泛关注。信号处理算法包括开环算法和闭环算法,开环算法主要有反正切法[8]和CORDIC(Coordinate Rotation Digital Computer)算法[9-11],闭环算法[12-14]主要是基于锁相环的角度观测器法[15-16]。
在使用反正切法对角度进行计算时,外围电路的配置相对简单,对硬件配置的要求不高。但是其包络信号易受到外界噪音干扰,在转换时精度较受影响。CORDIC算法[17]需要对输出的信号进行空间坐标变换和反复迭代运算,计算过程复杂且容易出现延迟。基于锁相环的角度观测器法[18]是将测量角度与估计角度进行比对,同时对两个角度进行误差计算,在误差趋于零时得到位置角度。该方法能准确跟踪转子的角速度,持续更新观测值,系统性能平滑,信号失真影响较小、抗干扰能力强以及解算精度较高。
1 传统闭环解码系统
如图1所示,传统闭环解算系统是将双通道旋转变压器的精机、粗机以及励磁参考电压RH、RL分别与内部微型变压器相连[19],转换成S1/S′1、S2/S′2、S3/S′3、S4/S′4这4个引脚端的粗机和精机的二路正余弦信号形式

图1 传统的闭环解码系统Figure 1. Traditional closed-loop decoding system
(1)
式中,k为粗机的互感与自感之比;k′为粗机的互感与自感之比;E为励磁电压幅度;US1-S3、US2-S4、US′1-S′3、US′2-S′4为电压;ω为励磁电压角频率;θ为精机的旋转角度;pθ为粗机的旋转角度。
通过闭环解码算法分别算出精机与粗机的角度数字信号,然后通过双速处理器进行误差抑制与粗精结合,最后输出组合后的角度数字信号。
2 传统闭环解码算法
角度观测器法采用比例积分控制,具有平滑输出的特点[20]。随着解码技术的发展,一阶角度观测器算法逐步淘汰,大多以二阶状态观测器进行解码。微型变压器将粗机的两路信号(US1-S3、US2-S4)解调后,经乘法器与估计值相乘,放大后作差,得到估计值与真实值的误差,通过控制φ的值来观测误差sin(θ-φ),当θ-φ=0时得到转子的位置。整个过程形成一个闭合回路(简称闭环解码),其计算过程如图2所示。
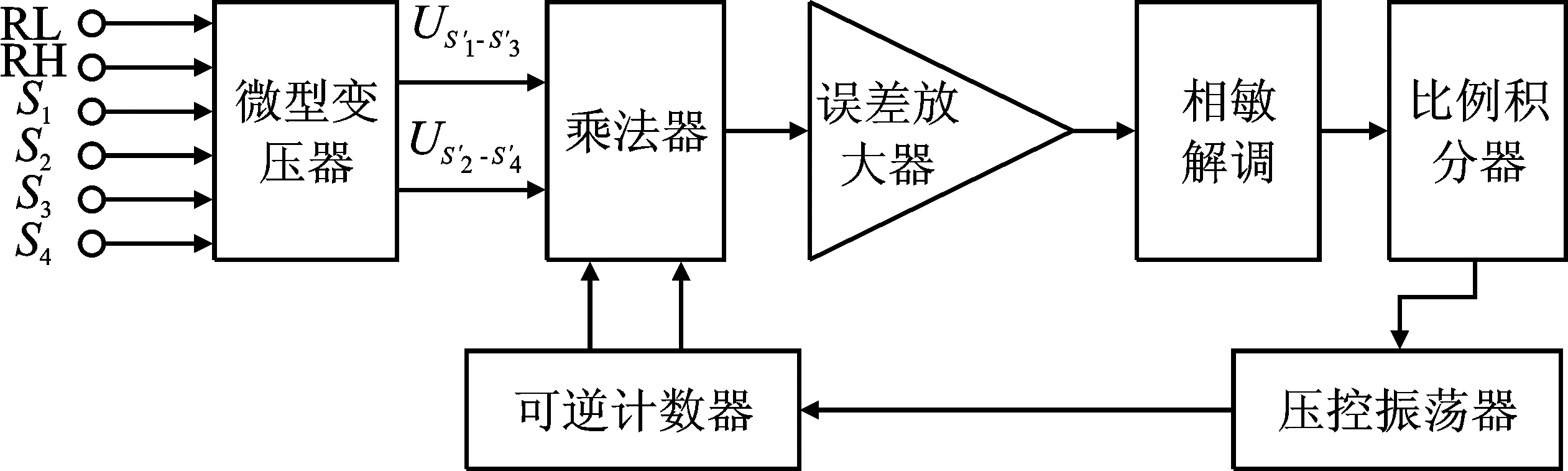
图2 闭环解码过程原理Figure 2.Principle of closed-loop decoding process
假定可逆计数器当前状态为φ,将式(1)中1、2式分别与估计转子位置的cosφ、sinφ相乘可得
(2)
这些信号经误差放大器相减,得到估计值与真实值的误差ε,如下所示。
ε=kEsinωtsinθcosφ-kEsinωtcosθsinφ=kEsinωt(sinθcosφ-cosθsinφ)=kEsinωtsin(θ-φ)
(3)
2.1 角度观测器观测过程
采用二阶状态观测器观察角度观测误差sin(θ-φ)。其中,φ是角度观测值,θ是实际角度值。若假设角位置为θ、角速度为ω,解调后的信号为
(4)
若θ=φ,则其之间的关系如式(5)所示。
(5)
式(4)为量测方程,以式(5)为状态方程对角位置和角速度进行状态观测,可得到观测器的基本形式为
(6)
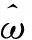
(7)
对式(7)进行离散化处理,可得到
(8)
式中,sinθe(j) =θe′(j)-θe′(j-1);θe′(j)、ωe′(j)为t=jTs时刻的角位置和角速度估计值。
2.2 数学模型
将上述计算过程转化成模型,可得到角度观测器模型,即传统的闭环解码算法数学模型,如图3所示。
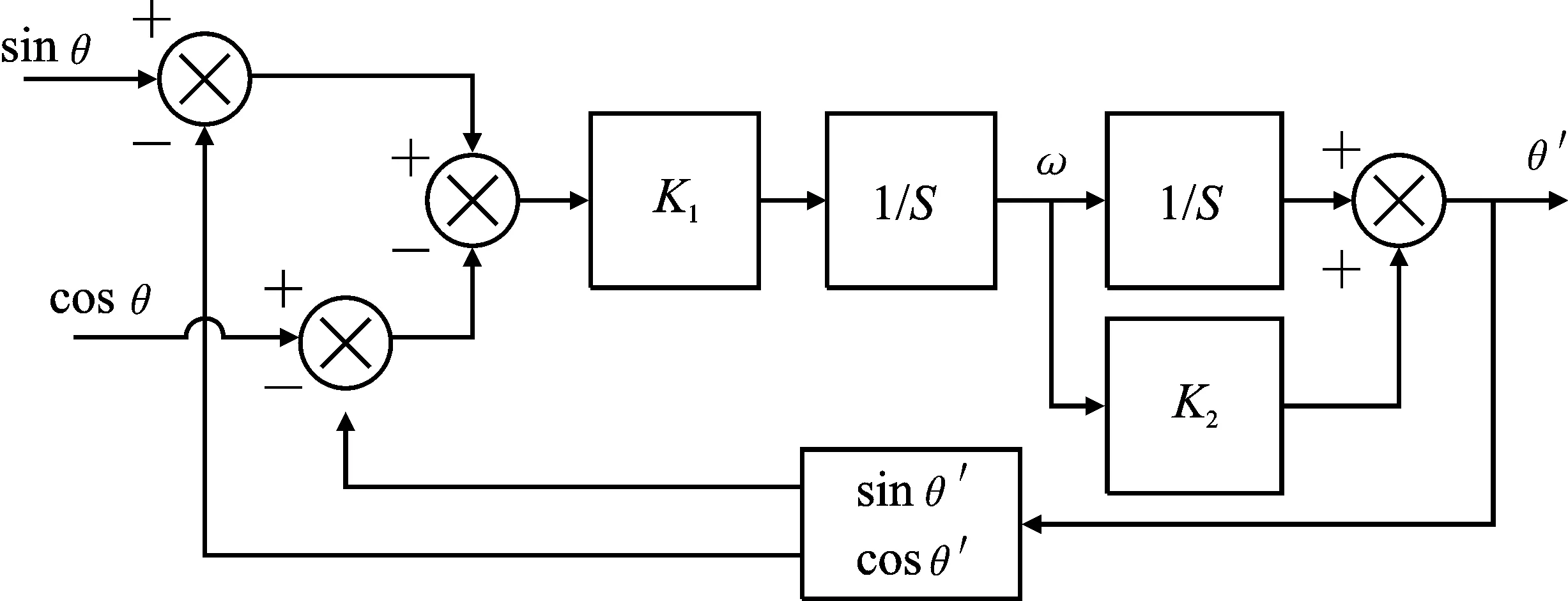
图3 传统的闭环解码算法数学模型Figure 3. Mathematical model of traditional closed-loop decoding algorithm
其开环传递函数为
(9)
其闭环传递函数为
(10)
2.3 稳态性能分析
解码系统需要考虑两个因素:1)量测方程出现的误差,即解码前信号参数的处理;2)稳态误差处理。为优化解码系统的稳定性能及解码能力,从两方面对传统的闭环解码算法进行分析。
1)二阶状态观测器使用的量测方程是一个理想状态,理想的旋转变压器信号没有误差。但在实际工作中,不可避免地会存在摩擦、噪声以及间隙,从而使信号中存在幅值、偏置和相位误差,所以需要对解码前信号参数进行处理,以确保误差不会影响到解码结果。
2)采用时域分析法[21]对传统的闭环解码算法进行稳态性能分析,找出可以进行改进的切入点,从而优化闭环解码算法。
由式(10)可得到传统的闭环解码算法误差传递函数为
(11)
误差为
(12)
系统的稳态误差为
(13)
当系统静止,即当R(S)=A/S时,e1=0。其中,A为正常数。系统匀速运行,即当R(S)=A/S2时,e1=0。当系统加速运行,即当R(S)=A/S3时,e1=A/K1。可以发现,采用传统的闭环解码算法,系统静止或匀速运行时,采用状态观测器确实能消除信号中存在的误差。然而当系统加速运行时,动态响应较慢,出现一定的稳态误差。
3 改进后的闭环解码算法
本文提出了一种改进后的闭环解码算法,主要进行了两方面的改进:1)在闭环解算之前,先使用最小二乘法对旋转变压器输出的信号参数进行数据拟合,以进行辨别与校正,然后使用二阶状态观测器对其进行解码;2)为避免加速时造成的稳态误差,抑制参数波动及非线性因素对系统性能的影响,在二阶状态观测中设计校正装置对其进行校正,以减小稳态误差。
3.1 最小二乘法进行数据拟合
传统的闭环解码算法以式(2)为量测方程,这个量测方程是基于理想状态下才会产生的信号。当速度变化时,由于旋转变压器自身的工艺以及外在的环境,使其偏离理想信号,产生幅值、偏置以及相位误差,因此需要对输出的信号进行数据拟合,使其无限接近理想状态信号,即旋转变压器真实的信号。最小二乘法[22]是数据拟合中常用的方法,它能根据数据的随机影响而使产生的误差最小化。基于此,改进后的闭环解码算法在进行解码之前设计最小二乘法拟合数据,使其拟合成旋转变压器真实的信号,减少误差的产生。
假设在信号传递过程中,幅值误差为A1、A2,偏置误差为B1、B2,相位误差为Ф,则式(4)可表示为
(14)
将此信号分解到平面上,出现的样本点分布为椭圆。利用椭圆参数的性质进行数据拟合,使其输出的信号尽量接近理想值,得到校正后的信号为
(15)
椭圆方程为
F(x,y)=x2+Axy+By2+Cx+Dy+E=0
(16)
现采集到了多个待拟合点Pi(xi,yi),根据最小二乘法的原理,则拟合的目标函数为
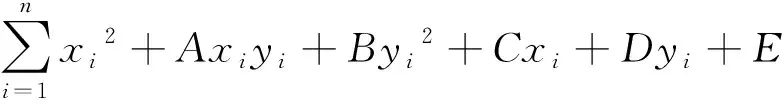
(17)
为使F到该椭圆的距离之和最小,即点到假设椭圆的误差最小,需要使F的各项偏导数为0,可求得A、B、C、D、E的矩阵表示形式,即
(18)
根据式(17)可解得A、B、C、D、E的参数值,此拟合后的数据能使信号传递过程中误差最小化,将拟合后求得的参数代入式(14)中,求得的量测方程更接近旋转变压器的真实信号,为下一步解码做准备。
3.2 校正装置
传统闭环解码算法在速度恒定时,稳态误差几乎为零,但随着时间和速度的改变,信号传递过程中会出现功率损耗和扰动,导致系统的性能变差、稳定性降低。为避免发生这种情况,在通道中能量较低的部位设计校正装置以保证系统的稳定。
假设校正装置的传递函数为D(S),则加入校正装置后的传统的闭环解码控制图,如图4所示。
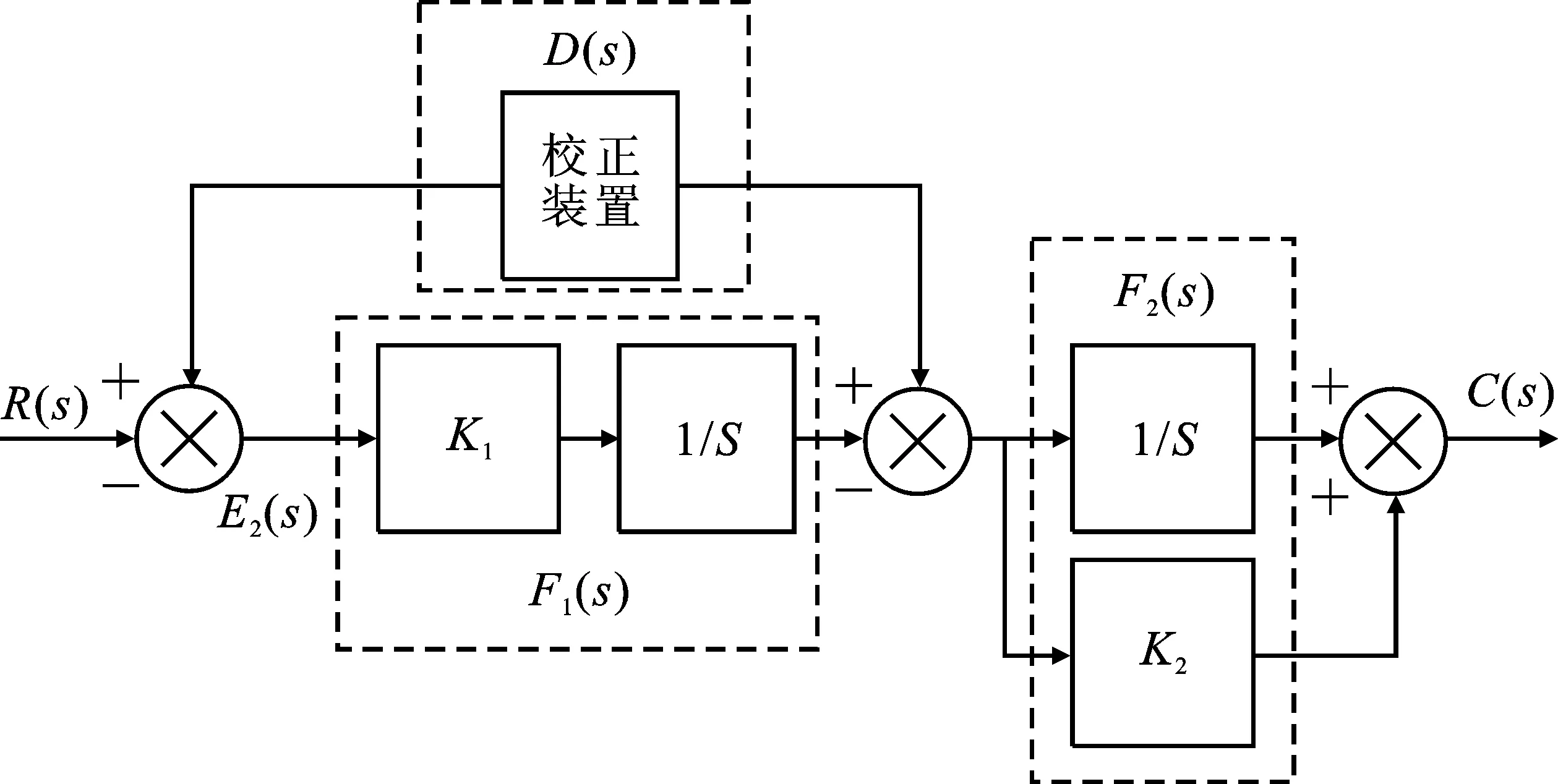
图4 校正装置控制Figure 4. Correction device control
在图4中,此控制系统中输出与输入之间的关系为
C(S)=[E2(S)F1(S)+R(S)D(S)]F2(S)
(19)
系统的误差传递函数为
E2(S)=R(S)-C(S)
(20)
将式(19)代入式(20),求得
(21)
若要使输出与输入误差E2(S)为0,只需要使

(22)
求得D(S)为F2(S)的导数。为避免微分中的噪声干扰,可设置一阶滤波器进行滤波。可将校正装置设置成
(23)
式中,T为滤波器时间常数。
3.3 改进后的闭环解码算法数学模型
综合以上分析,得到改进后的闭环解码算法数学模型,如图5所示。

图5 改进后的闭环解码算法数学模型Figure 5. Mathematical model of improved closed loop decoding algorithm
将式(9)与式(23)组合可得改进后的闭环系统开环传递函数为
(24)
闭环传递函数为
(25)
系统的误差传递函数为
(26)
系统误差为
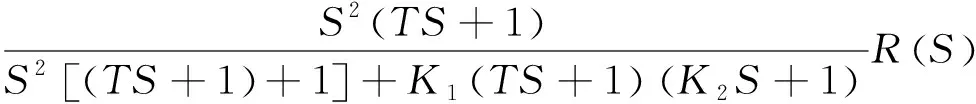
(27)
则系统的稳态误差为
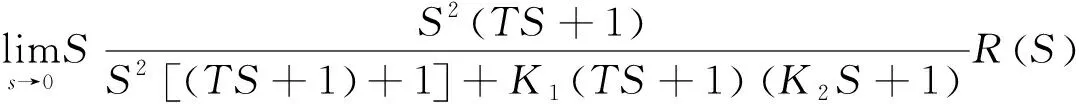
(28)
当输入加速信号,即R(S)=A/S3时,由式(28)求得e1=0。可以知道,改进后的闭环解码算法不论匀速、加速,系统稳态误差都趋于0。
4 仿真实验
采用MATLAB仿真环境对两种闭环解码算法的时域分析情况进行仿真,当输入r(t)=20t时,时域响应曲线如图6所示。
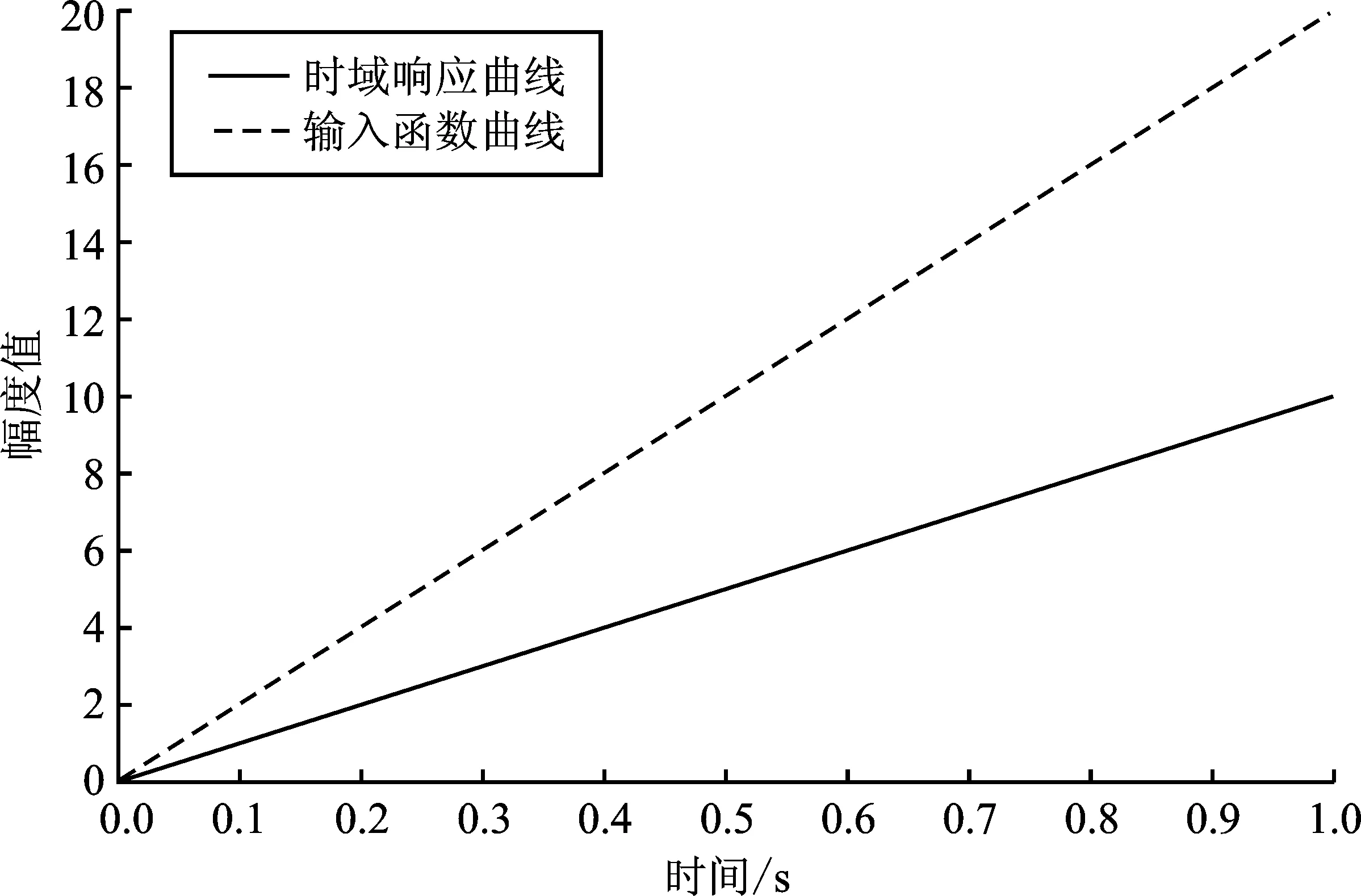
(a)
当输入匀速信号时,传统的闭环解码算法和改进后的闭环解码算法的时域响应曲线基本相同,实验结果表明系统的稳态误差相差不大。
当输入r(t)=10t2时,时域响应曲线如图7所示。实验结果表明,采用改进后的闭环解码算法时,输入函数曲线和时域响应曲线稳态误差明显小于采用传统的闭环解码算法。由此可知,采用改进后的闭环解码算法稳态误差更小、系统更稳定。
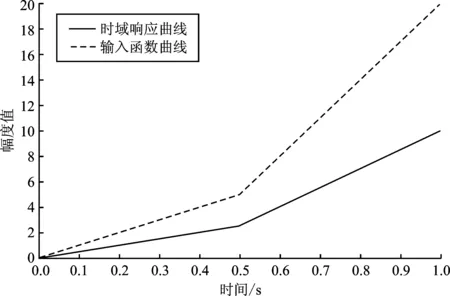
(a)
搭建动态仿真环境,设定K1=10 000,K2=0.014 14,T1=0.03 s,验证两种解码算法对角速度和角位置误差的影响情况。当速度为20 rad/s时,输出角位置误差曲线如图8所示,输出角速度误差曲线如图9所示。
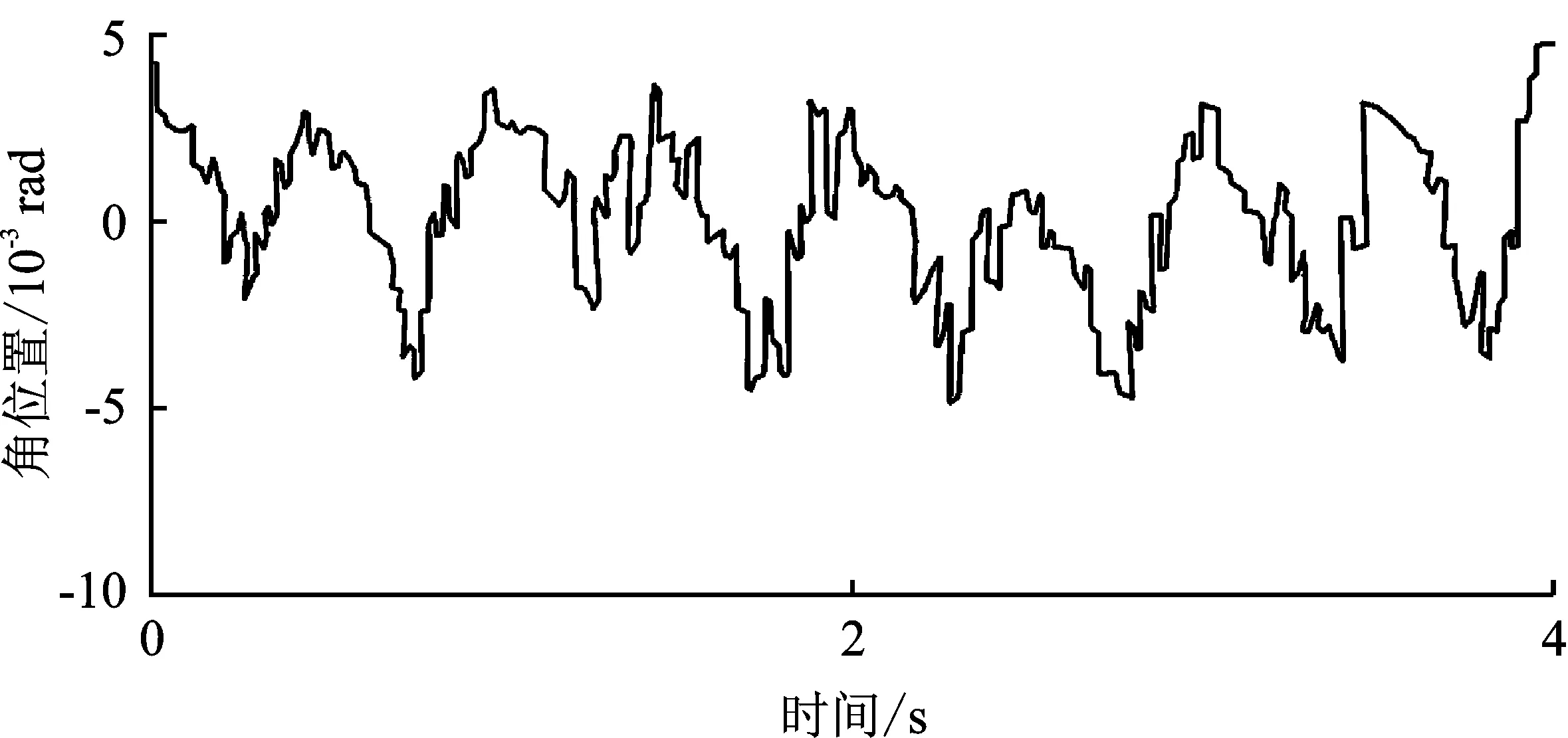
(a)
从图8和图9可以看出,当系统处于匀速时,两种解码算法解算出的角位置误差和角速度误差基本上变化不大。
当速度为10trad/s时,采用两种解码算法的输出角位置误差曲线如图10所示,输出角速度误差曲线如图11所示。

(a)
从图10和图11可以看出,当系统处于加速时,传统的闭环解码算法角位置误差在(-10,0)之间波动,角速度误差在(-0.5,-0.2)之间波动。改进后的闭环解码算法角位置误差在(-4,3)之间波动,角速度误差在(-0.15,0.10)之间波动。由此可知改进后的闭环解码算法角位置、角速度误差更小。
5 结束语
本文分析了改进后的闭环解码算法分别在匀速、加速条件下的时域响应情况,对角位置和角速度误差进行了仿真实验。实验结果表明,在系统匀速时,改进前后两种算法都能准确解算出角位置和角速度,稳态误差几乎相同。但是,当系统加速时,改进后的闭环解码算法解算出的角位置和角速度的偏差比传统的闭环解码算法小。

