六相全桥逆变器驱动PMSM的简化模型预测电流控制

袁庆庆,吴瑞麒,马 婷,谢晓彤

(1.上海理工大学 机械工程学院,上海 200093;2.国网宁夏电力有限公司 经济技术研究院,宁夏 银川 750004)

与传统电机驱动系统相比,多相电机驱动系统具有转矩脉动小、容错能力强、母线电压利用率高以及控制资源多等优点,适用于各类要求高可靠性场合[1-3]。全桥逆变电机驱动(或称开绕组结构)各相电气隔离,具有较好的容错性能和较低的开关器件功率,近年来在容错电机驱动应用中受到广泛关注[4-6]。然而,由于电压矢量的增加(六相全桥逆变电机驱动有729个电压矢量)以及谐波和零序电流分量的影响(当逆变器采用单直流母线时,零序电流分量不可忽略),传统三相电机驱动的控制策略无法直接移植。

多相逆变电机驱动系统的脉宽调制(Pulse Width Modulation,PWM)策略主要有两种:空间矢量PWM(Space Vector Pulse Width Modulation,SVPWM)和载波PWM(Carrier Pulse Width Modulation,CPWM)。文献[7]提出的多相系统采用扩展三相SVPWM,为减少电压矢量过多造成的计算负担,选取最大电压矢量作为基本矢量,但产生了不可控的谐波电流分量。为了实现转矩控制和谐波抑制的目的,文献[8]首次提出了矢量空间解耦(Vector Space Decomposition,VSD)理论,将电磁和非电磁分量解耦到多个正交的二维子平面。文献[9]综合考虑到转矩控制、谐波抑制和中点电位平衡控制等问题,通过重构解耦的电压矢量候选组,提出了一种新的用于双三相三电平电机驱动的SVPWM策略。虽然通过矢量化简可以在一定程度上解决电压矢量增加的问题,但即使将VSD理论应用到SVPWM中仍存在扇区判断复杂、计算量大等问题[10-12]。与SVPWM相比,CPWM方法实现简单,不会随着相位数的增加而增加控制难度。文献[13]针对五相开绕组驱动系统研究并比较了各种CPWM方法。

共直流母线供电的多相电机定子电流中存在固有的谐波和零序分量,从而影响输出转矩性能[14-16]。近年来,模型预测控制(Model Predictive Control,MPC)方法以其动态响应佳、适用于多目标优化控制等优点在电气工程领域得到了广泛应用[17],也应用于多相电机驱动控制[18]。考虑多相驱动系统中逆变器输出电压矢量数目、冗余情况复杂,在应用MPC算法时,计算量会随着相数的增加而显著增加,因此在实际应用中需要进行适当简化。

本文以共直流母线供电的六相全桥逆变器驱动六相永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)为研究对象,提出了一种简化模型预测电流控制(Model Predictive Current Control,MPCC)策略。首先基于VSD理论将六相全桥逆变器输出的729个电压矢量分解到基波、谐波及零序子空间,然后结合数学模型和拓扑特性,深入分析了不同子空间上电压矢量的约束关系。在此基础上以基波电流控制、谐波与零序电流抑制为目标,对逆变器输出矢量进行了二级优化,将729个矢量简化为12个,既能保证不同工况下的控制性能,又能在较大程度上提高执行效率。最后,通过不同控制方法下的对比实验对该简化MPCC策略进行验证,并对不同控制策略下的执行时间进行测试,为其易于数字化实现提供依据。

1 系统建模

本文所提六相全桥逆变器驱动永磁同步电机的结构如图1所示。直流母线电压为Vdc,两套定子绕组间相隔30°电气角度,六相之间无电气连接。

图1 六相全桥逆变器驱动六相PMSM结构Figure 1. Configuration of six-phase full-bridge inverter fed PMSM drive

结合如式(1)所示的矢量空间解耦变换,该六相全桥逆变器在自然坐标上的六维变量可分解映射到3个正交子空间上,即αβ子空间、xy子空间和零序o1o2子空间。

(1)

αβ子空间为基波子空间,包含基波和12k±1(k=1,2,3,…)次谐波分量,参与机电能量转换。xy子空间为谐波子空间,包含6k±1(k=1,3,5,…)次谐波分量,不参与机电能量转换但会造成定子电流严重畸变。o1o2子空间为零序子空间,包含3k(k=1,3,5,…)次谐波分量,不参与机电能量转换[19-21]。本文研究的六相全桥逆变器为共直流母线结构,零序分量的存在也会对定子电流造成影响[22],需要进行抑制。

为便于电机控制,将基波子空间分量变换至同步旋转dq坐标系下,对应的电压和磁链方程为

(2)

(3)

式中,Rs为定子电阻;Ld和Lq为d轴和q轴电感,Ld=Lq=L;ψd和ψq为dq子空间上的磁通分量;ψf为永磁磁通;ωe为转子电角速度。

同样地,电机在xy子空间上的电压方程为

(4)

式中,ux、uy和ix、iy分别为xy子空间上的定子电压和电流分量;Lz为漏感。

对于共直流母线的全桥逆变器来说,定子绕组中的零序电流分量可以认为是由调制产生的共模电压ucom(如式(5)所示)与电机本身反电动势的谐波分量相互作用产生,以A相为例,对应的等效零序电路如图2所示。

图2 A相等效零序电路Figure 2. A-phase equivalent zero-sequence circuit

ucom=(uA+uB+uC+uU+uV+uW)/6

(5)

其中,i0表示定子绕组中的零序电流分量,3ωeψ3fsin(3θe)表示PMSM反电动势的3次分量。则该零序电路的电压方程可表示为

(6)

2 逆变器输出电压矢量

图1所示的六相全桥逆变器有36=729种不同的开关状态。以A相(如图3所示)为例,定义开关状态S为

图3 A相全桥逆变电路Figure 3. A-phase full bridge inverter circuit

(7)

其中,T1、T2、T3和T4为A相的4个开关。

根据矢量空间解耦理论,逆变器输出电压矢量在基波、谐波以及零序子空间上的合成定义为

(8)

(9)

(10)

式中,e为欧拉数。

电压矢量在αβ和xy子空间上的分布如图4所示。

(a)

这729个电压矢量在αβ和xy子空间上分布相似,但具体位置不同。取αβ子空间上的向量进行冗余分析,共有361个非冗余电压向量,具有24个不同的幅值,可因此标记为24层。各层对应的矢量幅值和个数如表1所示。

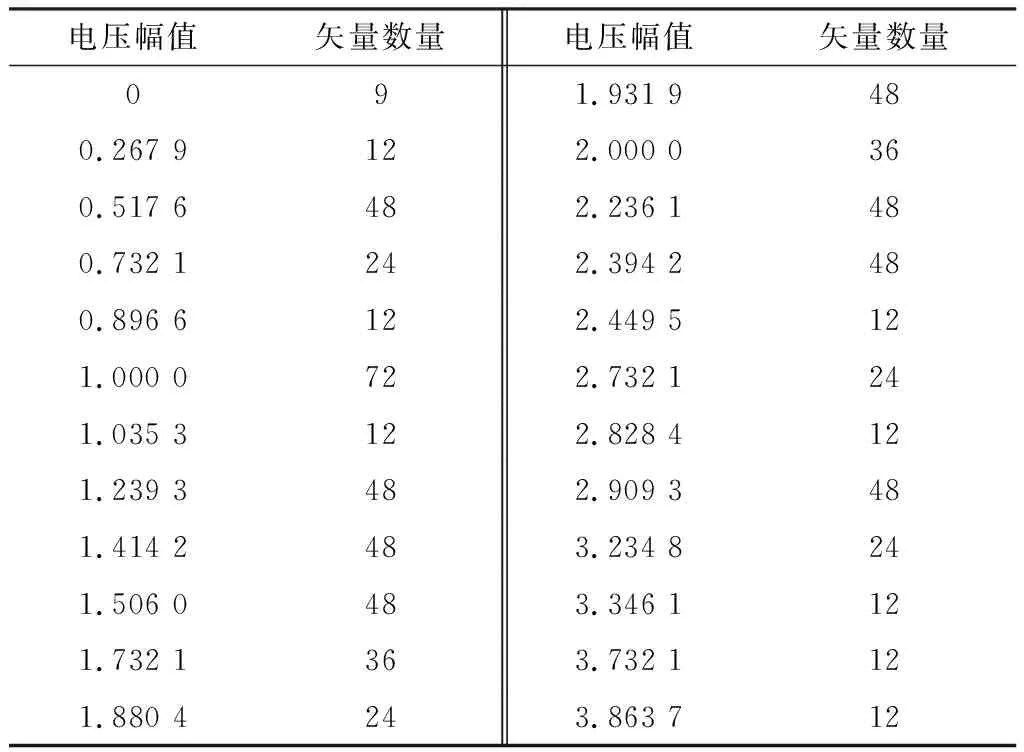
表1 αβ子空间上的矢量分布(假设Vdc/3=1 V)Table 1. Vector distributions on αβ subplace(Hypothesis Vdc/3=1 V)

xy子空间上的矢量分布与αβ子空间相似,但同一电压矢量的映射位置与αβ子空间上的映射位置不同。

分别在αβ子空间取幅值为3.863 7和0.732 1的两个电压矢量,进一步比较相同矢量在不同子空间的映射关系。在xy子空间的幅值分别为1.035 3和2.732 1,如图5所示。此处729个电压矢量根据开关状态从[-1 -1 -1 -1 -1]到[1 1 1 1 1 1]标记为1到729。例如,状态为[-1 -1 -1 -1 -1 -1]的矢量标记为1,状态为[-1 -1 -1 -1 0]的矢量标记为2,状态为[1 1 1 1 1 0]的矢量标记为728,状态为[1 1 1 1 1 1 1 1 1]的矢量标记为729。

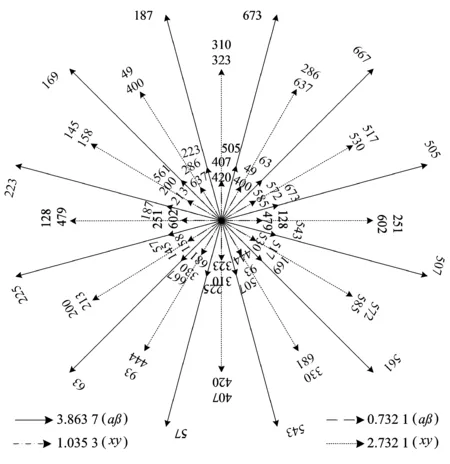
图5 相同矢量在αβ和xy子空间上的映射关系Figure 5. Mapping relationship of the same vectors on αβ and xy subplaces

相同矢量在不同子空间的映射位置之间存在差异,需要进行控制约束。

3 简化模型预测电流控制策略

由于六相全桥逆变器输出电压矢量数量多,冗余和约束条件复杂,本文提出了适用于该逆变器驱动电机系统的两级矢量优化的简化模型预测电流控制策略。

3.1 一级矢量优化

为了提高直流母线电压利用率,限制逆变器产生的谐波,在αβ子空间上的合成电压矢量应尽可能大,而在xy子空间上的合成电压矢量应尽可能小[23]。因此,一级优化首先选取在αβ子平面上幅值大于在xy子平面上幅值的矢量作为候选矢量,最终筛选出表2中的第13、16、18、20、21、22、23、24层(共228个向量)。

表2 αβ子平面和xy 子平面上所有729个电压矢量的映射关系(假设Vdc/3=1 V)Table 2. Mapping relationship of all 729 voltage vectors on αβ subplace and xy subplace(Hypothesis Vdc/3=1 V)

3.2 二级矢量优化

为降低定子绕组中的零序电流分量,需要抑制系统中的共模电压分量,将式(6)改写为

(11)

为了降低共模电压ucom,SA+SB+SC+SU+SV+SW可设为0,因此可选择表3中的第13、20、22、24层(共42个向量)作为筛选后的矢量。

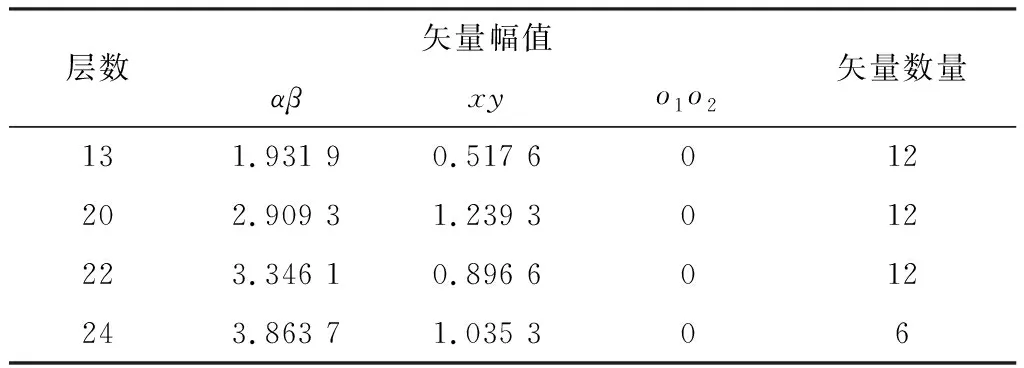
表3 初步二级优化后的候选矢量Table 3. Candidate vectors after preliminary secondary optimization

表3中的候选电压矢量虽然可以合成零共模电压,但却可能在ABC三相和UVW三相中存在直流偏置。为进一步降低相绕组中的零序分量,可进一步令

(12)

因此,最终选择表3中第22层的12个电压向量作为最终筛选后的候选电压矢量,对应的开关状态如表4所示。

表4 第22层矢量对应的开关状态Table 4. Switch status corresponding to layer 22

3.3 整体控制策略

本文的控制目标是不同子空间上的定子电流分量。根据式(3)～式(5),不同子空间的定子电流分量可离散化为

(13)

其中,Ed(k)=ωe(k)Liq(k),Eq(k)=-ωe(k)Lid(k)-ωe(k)ψf。

考虑基波与谐波子空间的电流控制目标,设计目标函数为

(14)

式中,基波与谐波控制的权重因子都设为了1,能在保证基波跟踪、谐波抑制的同时有效避免权重因子的设计权衡。

对应的整体控制如图6所示。

图6 两级矢量优化的简化模型预测电流控制Figure 6. Simplified model of two-stage vector optimization for predicting current control

4 实验结果

本文基于六相PMSM电机实验平台验证了所提控制策略的有效性。六相PMSM电机及控制系统参数如表5所示。对应的实验平台如图7所示,控制算法采用Xilinx Kintex7-FPGA控制板,以磁粉制动器为负载。考虑到安全因素,只比较和验证了正常的CPWM方法和本文提出的MPCC方法。

表5 六相永磁同步电机及控制系统参数Table 5. Parameters of six-phase PMSM and control system

图7 实验平台Figure 7. Experimental platform

4.1 加减速性能比较

首先,电机在无负载的情况下启动到额定转速(12 000 r/min),在t=1 s时减速到6 000 r/min。不同方法对应的转速和转矩响应如图8所示。

(a)

可以看出,在电机空载运行时,常规的CPWM和MPCC方法都具有较好的动态速度和转矩响应。相比较而言,MPCC方法的速度或转矩响应比常规的CPWM方法更平滑。

4.2 加减载性能比较

随后,进行电机的动态加减载测试,将电机转速设置为12 000 r/min,先加载至额定负载2.2 N·m,再减载为1.1 N·m,此时的动态电流、速度和转矩响应如图9和图10所示。

(a)

对比图9和图10可以看出,相较于基于CPWM和PI控制器的控制性能,MPCC方法特别是谐波和零序电流抑制方面效果更佳。

MPCC方法所选取的12个电压矢量的幅值在αβ子空间上为3.346 1,在xy子空间上为0.896 6。如图10(b)所示,在αβ子空间上具有良好的控制性能,如图10(c)所示,在±1 A范围内,在xy子空间上具有轻微的谐波分量。另一方面,虽然这12个矢量在o1o2子空间上的幅值为0,但由于存在电机产生的反电动势的三阶分量ψ3f,仍然存在一些零序电流分量,如图10(d)所示。

就速度和转矩响应而言,这两种方法都具有较好的动态性能。然而,MPCC方法具有更快的转矩动态响应和更平滑的波形。

4.3 不同转速下的定子电流THD比较

选取不同转速下的定子电流谐波性能进一步对比分析,此时电机带额定负载,对应的THD对比结果如图11所示。

可以看出,两种方法的THD性能都会随着电机转速的增加而增大,但总体来说,MPCC方法相较传统CPWM方法具有更好的THD性能。

5 结束语

本文针对六相全桥逆变器驱动多相永磁同步电机存在的多矢量控制和复杂冗余控制问题提出了一种基于二级矢量优化的简化模型预测电流控制算法。考虑驱动系统的共直流母线结构和六相电机的本质特性,本文的控制难点在于保证基波电流跟随性能的同时对定子电流中的谐波分量和零序分量进行抑制。本文在矢量空间解耦理论的基础上提出了同时考虑基波、谐波及零序分量的二级矢量优化方法,将逆变器输出的729个电压矢量优化至12个,并以此为基础了设计了模型预测电流控制算法。 与传统CPWM方法比较的实验结果表明,本文所研究的基于二级矢量优化的简化模型预测电流控制算法具有更好的动静态性能,能在保证基波电流跟踪性能的同时实现定子谐波和零序电流分量的有效抑制,可为多相电机驱动系统的研究提供一定的理论研究基础。