面向异构信号处理平台的量子调度算法

沈小龙,马金全,胡泽明,李 娜,李宇东

(1.战略支援部队信息工程大学 信息系统工程学院,河南 郑州 450000;2.交通银行 河南省分行,河南 郑州 450000)

随着科学技术的发展,现代信号处理应用对硬件资源的处理速度要求越来越快,精度要求越来越高,内存要求越来越大,且不同类型应用所需的硬件资源类型不相同。传统信号处理平台硬件资源类型单一、搭载的信号处理应用类型少、处理能力有限以及面对上述硬件资源要求无解决方法,而异构信号处理平台凭借自身丰富处理资源[1-4]成为现代信号处理应用的首选搭载平台。将信号处理应用部署在异构信号处理平台时,首先利用有向无环图(Directed Acyclic Graph,DAG)将应用抽象建模为有依赖关系的任务集合[5-7],然后通过调度算法将任务部署到平台的处理器上,不同的部署方案应用执行完成时间差别较大。调度算法的优劣决定应用实时性高低和平台工作性能好坏。因此设计一种使应用完成时间尽可能短、实时性尽可能高的调度算法是该领域的研究热点。

调度算法在运行时主要分为任务优先级排序和处理器分配两个阶段。根据DAG平均通信开销和平均计算开销的比值(Communication to Computation Ratio,CCR)将应用分为计算密集型和通信密集型[8]。文献[9]提出HEFT(Heterogeneous Earliest Finish Time)算法,该算法是较为经典的调度算法,通过任务平均计算开销计算得到任务序值并进行排序,忽略不同处理器处理性能差异,对通信密集型任务调度效果较好,但对计算密集型任务调度效果不佳,且其任务处理器分配策略单一。文献[10]提出HSIP(Heterogeneous Scheduling Algorithm with Improved Task Priority)算法,该算法在HEFT基础上进行改进,在计算任务优先级时,利用计算开销标准差代替平均值,充分反映任务在不同处理器运行时的计算开销差异,对计算密集型应用调度效果较好,但对通信密集型应用调度效果一般。文献[11]提出任务优先级分流排序策略,根据应用类型特点制定不同排序方法,但该算法处理器分配方案较为复杂且算法复杂度高。文献[12]提出的算法对初始信息素矩阵较为依赖。量子算法具有较好的性能,在密码和神经网络优化领域得到广泛应用。文献[13]利用量子比特进行传输协议制定,并通过量子旋转门设计传输机制。文献[14]和文献[15]均是用量子算法优化BP(Back Propagation)神经网络的阈值和权值参数,提升网络准确率。文献[16]将量子算法与生成对抗网络结合,提升网络训练速度。

当前量子算法在异构信号处理平台任务调度领域研究较少。结合上述调度算法的研究现状,本文提出一种面向异构信号处理平台的量子调度算法(Quantum Scheduling Algorithm,QSA)。该算法利用量子比特对任务分配方案进行编码,并通过量子旋转门更新分配方案。在任务优先级排序阶段,采用任务优先级分流排序策略确定任务调度顺序。在处理器分配阶段,采用任务复制思想和最早完成时间原则进行处理器分配。

1 系统模型

异构处理平台总体可分为4层[17],如图1所示。底层为硬件层,包含平台所有处理器资源。底层之上为中间层,由操作系统层、板级支持包以及平台抽象层等组成。中间层之上为组件层,包含项目组研发的所有组件。顶层为应用层,包含当前平台部署的信号处理应用程序。在异构信号处理平台增加新应用时,首先进行功能分析从组件库中挑选组件搭建应用程序,之后利用调度算法为应用程序中组件分配处理器,最后通过中间层将组件部署到相应处理器,完成新应用程序在异构处理平台的开发。

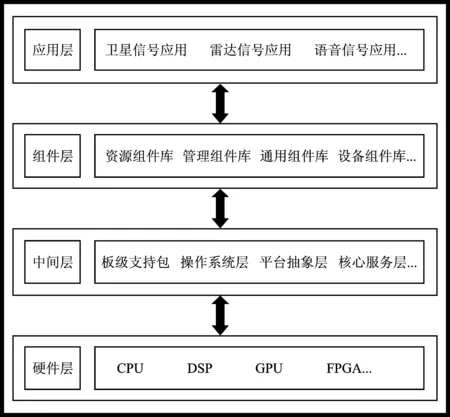
图1 平台结构Figure 1. Platform structure

在调度算法研究中,将信号处理应用抽象建模为DAG图,定义为G=(V,C,P,W)。其中,V是任务集合,C是通信开销矩阵,P是处理器集合,W是计算开销矩阵。经典DAG如图2所示。其中,vi为任务,与图中节点对应,cij为任务间平均通信开销,与图中有向边对应,pi为处理器,wij为任务在处理器上计算开销,与表1对应。

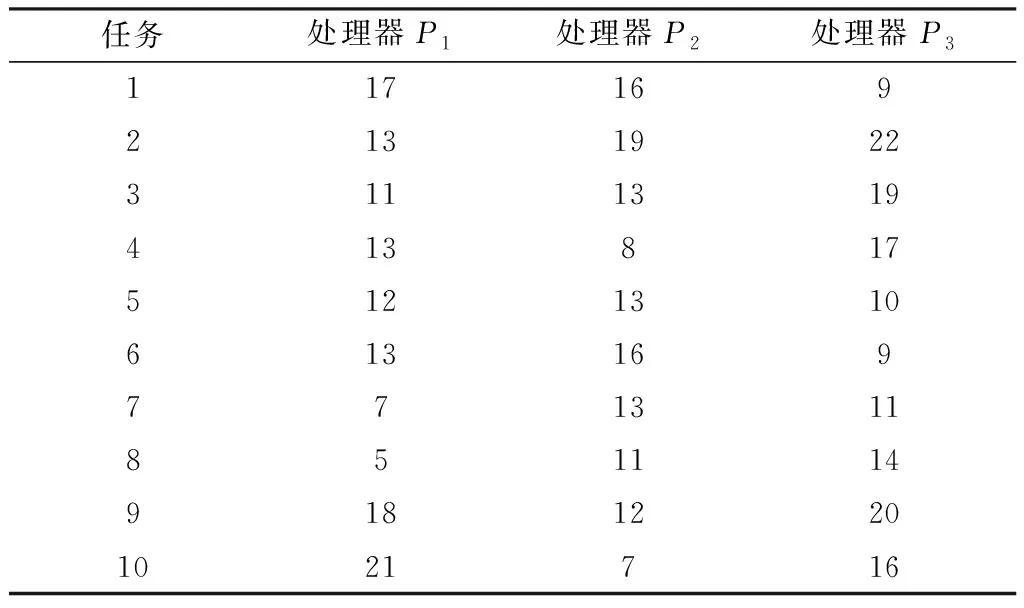
表1 典型DAG计算成本Table 1．Typical DAG calculation cost

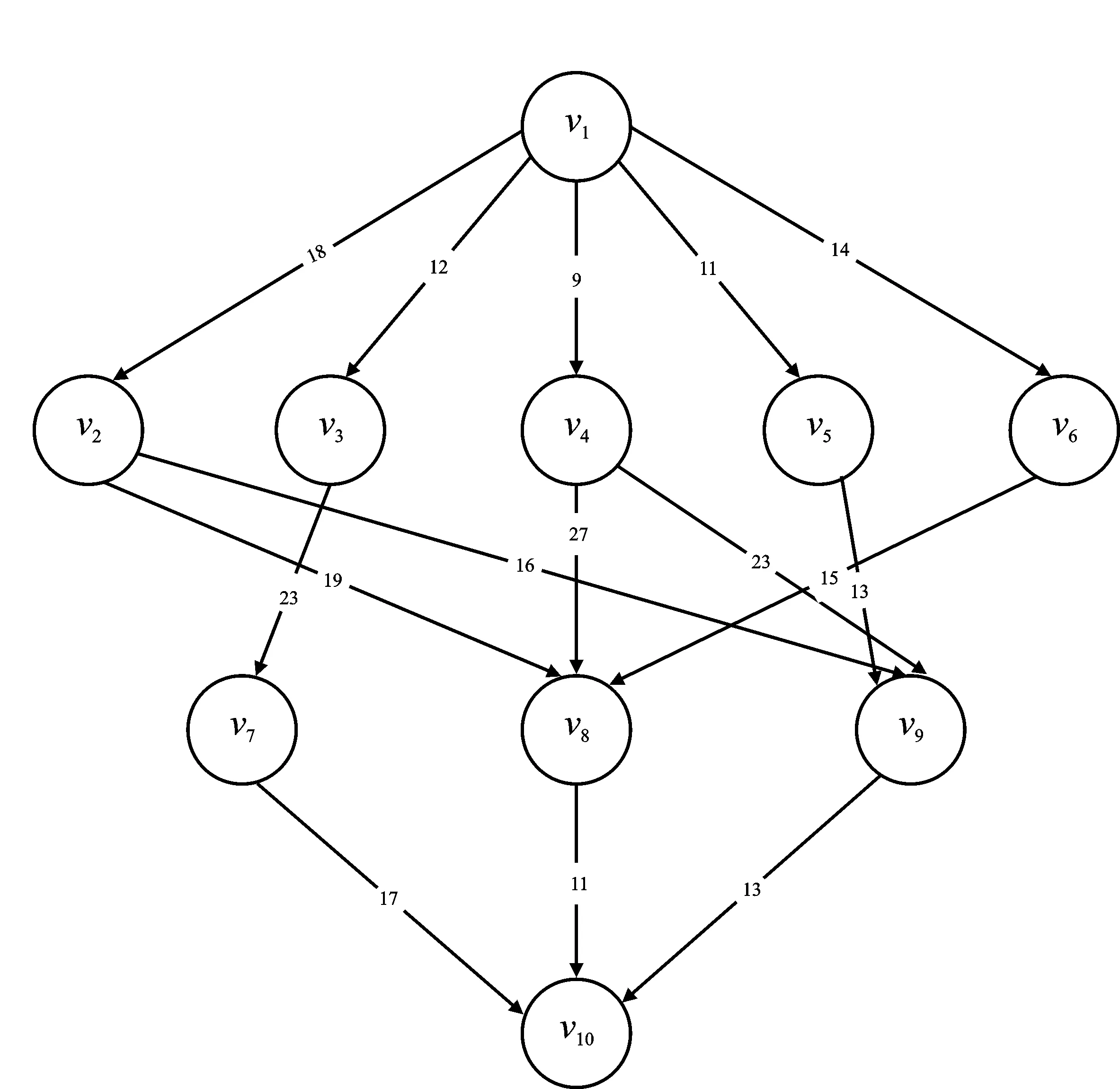
图2 典型DAG任务Figure 2. Typical DAG task

2 QSA算法

2.1 优先级排序

为能够得到更加符合任务类型特点的调度顺序,本文采用任务优先级分流排序策略,针对不同任务类型,优先级计算方法不同。得到任务图后首先计算该图CCR,计算式如下

(1)

其中,cij为vi与vj间通信开销;wik为vi在pk上计算开销;son(vi)为vi子任务集合;n为任务数;l为有向边数目;m为处理器数。CCR值≥1的是通信密集型任务,其余为计算密集型任务。通信密集型任务优先级计算式如下

(2)

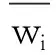
(3)

其中,σi为vi在所有处理器上计算开销的标准差,能更好地反映出任务在不同处理器上计算开销差异。得到任务优先级序值后,按照降序排序作为任务最终调度顺序。

2.2 量子比特编码

量子算法寻优能力较强,且不需要初始信息素。因此本文采用量子比特对任务处理器分配方案进行编码,编码中通过量子位来存储信息。量子位是由2个量子基态组成,其中一个是|0>态表示自旋向下态;另一个是|1>态表示自旋向上态,此二者是一对标准正交基。量子空间中的量子比特是这两个基态的叠加态|φ>

|φ>=A×|0>+B×|1>

(4)

其中,A和B分别表示处于各基态的概率幅,且满足如下计算式

|A|2+|B|2=1

(5)

量子比特可用基态矩阵和概率幅矩阵相乘的形式表示,计算式如下

(6)

本文实验的处理器数量取值范围是3～6,所以利用3个量子比特对任务分配的处理器进行编码,任务vi的编码方案如下

(7)

其中每对概率幅都满足式(5)。在具体情形中可根据处理器上限数量对量子比特编码位数进行调整。

在初始化任务分配方案的量子编码时,首先生成两个服从标准正太分布的随机数a和b,然后按照如下计算式

(8)

计算得到量子比特概率幅均满足式(5),通过产生的随机数增加种群多样性。

在得到编码方案后,生成一个0～1的随机数rand,并在每个量子比特中随机选取一个概率幅例如Ai1,将rand同Ai12进行对比,根据结果将该量子比特编码为二进制1或0,结果如下

(9)

在量子比特编码转换为二进制编码方案过程中,通过随机数进行比较,有助于跳出局部最优解。然后将该任务的二进制编码映射成为具体处理器编号。以将任务集合分配到3个处理器为例,对具体映射方案进行如下讲解。首先将式(9)中二进制转换为十进制数,因为每个任务的分配方案是用3个量子比特进行编码,所以转换为十进制后的取值范围是0～7,而处理器取值范围是1～3,因此按照如下计算式对十进制数进行映射

(10)

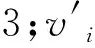
2.3 处理器分配

在进行处理器分配时,将任务分为入口任务、各处理器首任务和其余任务3类。

入口任务优先级最高,是第1个分配任务,其分配结果直接影响最终调度结果。本文采取最小计算开销原则对入口任务进行分配,将其分配到具有最小计算开销的处理器上,可以有效减少调度长度。

各处理器首任务是指分配到处理器上的第1个任务,对于该类任务利用任务复制思想优化任务完成时间。若首任务是入口任务则按照入口任务分配原则处理,若不是入口任务其执行开始时间前存在时间空隙,此时可以利用任务复制思想将其父任务复制到该处理器,同一处理器上任务间的通信开销可以忽略不计。通过任务复制能够有效减少任务间通信开销,进而优化任务完成时间。其余任务按照量子编码方案进行分配。

2.4 适度函数

本文将任务调度长度作为适度函数衡量每种分配方案优劣。同时每次迭代中适度函数的最优值是量子种群更新迭代得参考标准。调度长度计算式如下

makespan=EFT(vexit)

(11)

其中,vexit表示出口任务;EFT(vexit)表示出口任务的完成时间。调度长度即为DAG图的整体执行完成时间,该值越小越好。

2.5 量子比特更新

通过量子旋转门对量子比特进行更新,使更新后量子比特的概率幅仍然满足式(5),量子旋转门quantum_gate计算式如下

(12)

式中,θ为旋转角,其大小一般是π/25[18],通过将每种分配方案同最优适度函数方案进行对比后确定方向。图3为量子旋转,该图中横坐标是|0>态,纵坐标是|1>态,A和B分别表示处于各基态的概率幅,逆时针旋转为正方向,顺时针旋转量子比特的二进制编码同最优解的二进制编码进行比较,决定量子旋转角。

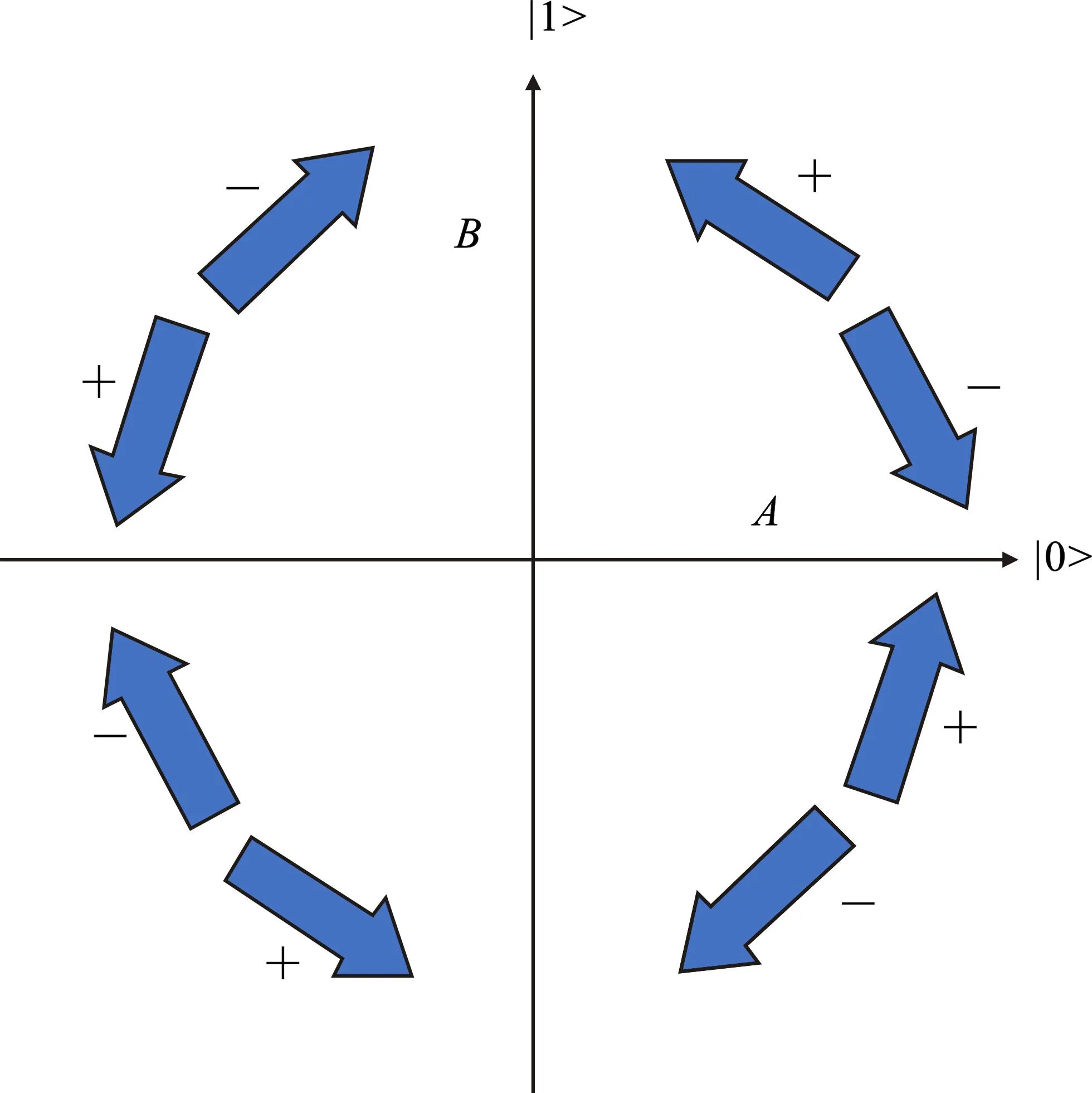
图3 量子旋转Figure 3. Quantum rotation

在量子比特同最优解的二进制编码比较时,将二进制的0和1等效于量子比特的|0>态和|1>态。

表2为具体情况下旋转角取值。得到旋转角后,按照如下计算式进行量子比特旋转

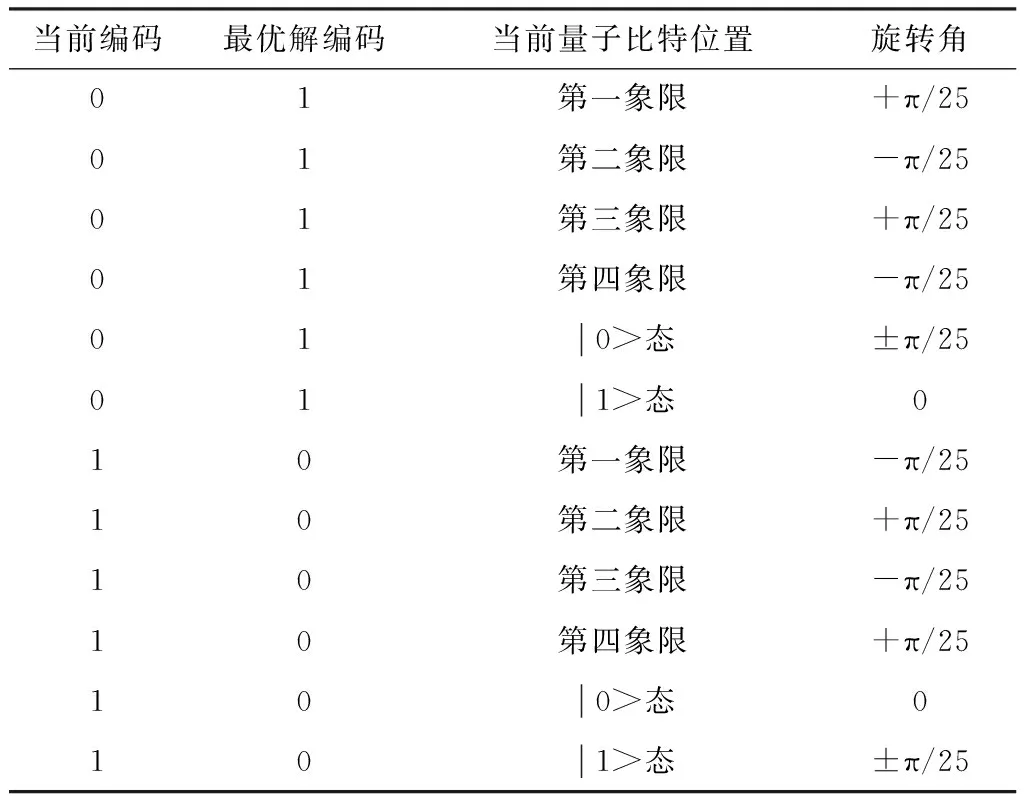
表2 量子旋转角取值Table 2. The value of the quantum ration angle

表3 QSA算法参数设置Table 3. QSA algorithm parameter settings

(13)

其中,Ai1和Bi1是旋转前的概率幅;Ai1′和Bi1′是旋转后的概率幅。图4为QSA算法流程。

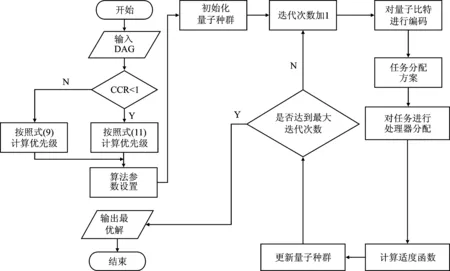
图4 QSA运行流程Figure 4.QSA operation flow

3 仿真实验及性能分析

3.1 参数设置

算法中的参数设置如3所示,量子种群为30,迭代次数为1 000,量子比特编码长度为3。

3.2 QSA有效性分析

通过经典DAG和随机DAG进行仿真实验,将QSA同HEFT算法、HSIP算法和文献[11]所提算法进行对比,验证QSA的有效性。

实验1计算得到QSA算法的调度长度如图5所示。

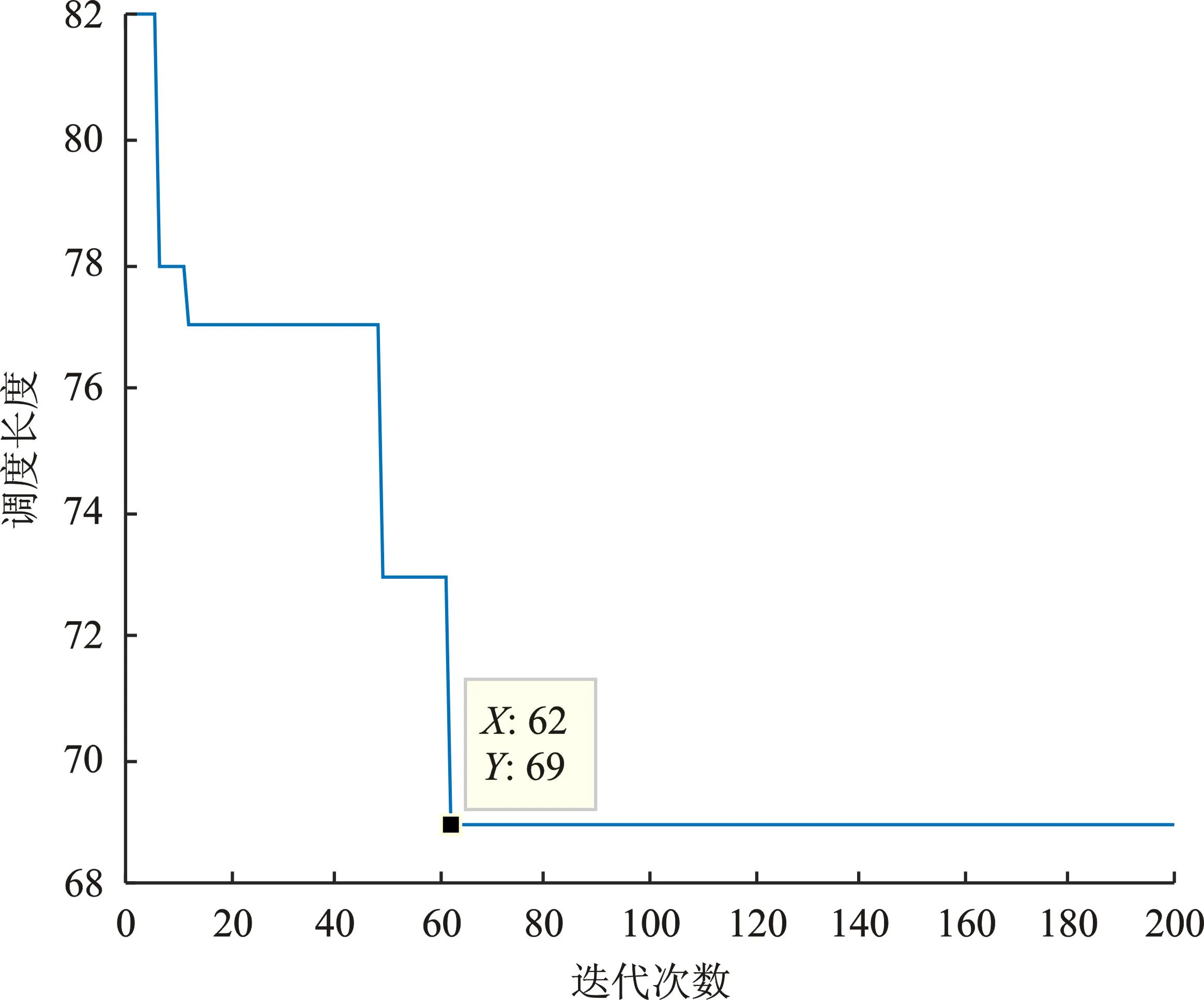
图5 实验1QSA调度长度结果Figure 5. QSA scheduling length result in experiment one

从该仿真结果看出迭代到62次时,QSA算法的调度长度值收敛于69。表4为4种算法的调度长度。

表4 实验1中4种算法调度长度结果Table 4. The four algorithms scheduling length result in experimont one

从调度结果看出,QSA算法的调度长度优于HEFT算法,但比HSIP算法和文献[11]所提算法较差。这是因为经典DAG任务少,体现不出QSA算法的计算性能。从图5可以看出,迭代到一定次数时陷入局部最优,调度长度保持不变,能跳出局部最优解在于将量子比特转换为二进制比特过程中生成的随机数,该过程提供了跳出局部最优的通道。

实验2随机生成一个任务数为20,处理器数为3的任务图,计算得到QSA算法的调度长度如图6所示。

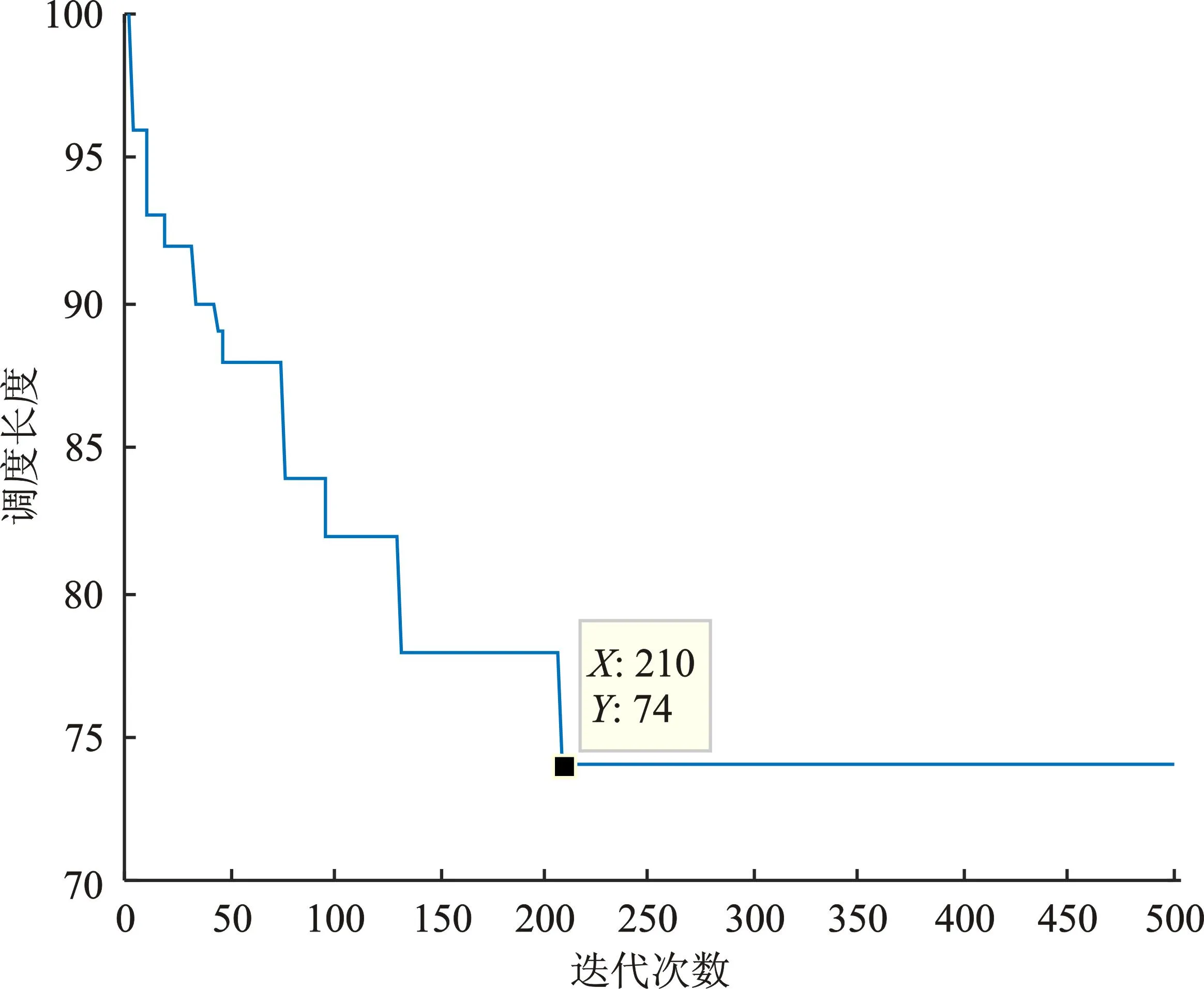
图6 实验2QSA调度长度结果Figure 6. QSA scheduling length result experiment two

从该仿真结果看出,迭代到第210次时,QSA算法的调度长度值收敛于74。表5为4种算法的调度长度。

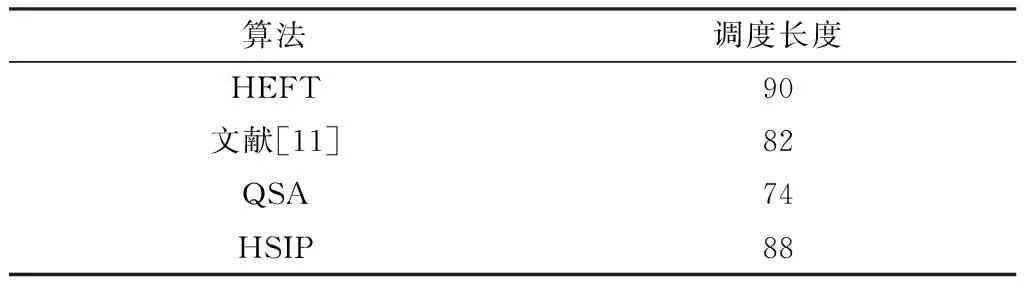
表5 实验2中4种算法调度长度结果Table 5.The four algorithms scheduling length result experiment two

从调度结果看出,QSA算法的调度长度均优于对比算法。

从以上实验看出,QSA算法对调度长度的优化效果有效、明显。

3.3 QSA可靠性分析

设计两组实验对任务数量和处理器数量分别进行变化,以验证QSA算法的可靠性。

实验3随机生成一组任务数为20,处理器数为3～6的任务图。计算得到结果对比如图7所示,并计算QSA算法相对于对比算法的优化率。

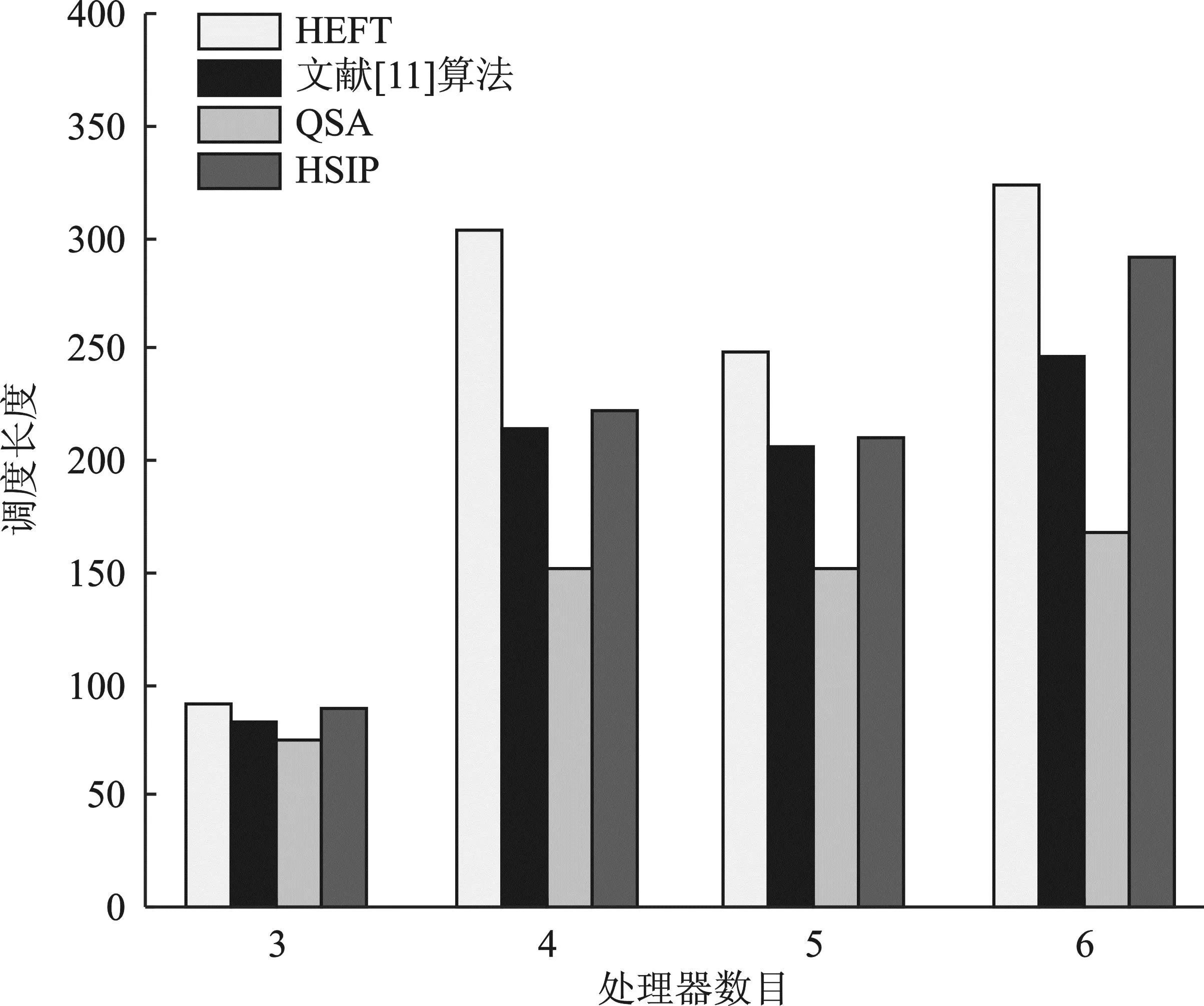
图7 实验3调度长度对比Figure 7. Comparison of scheduling length in experiment three

从调度结果可以看出,QSA算法的调度长度均优于HEFT、HSIP和文献[11]所提算法,对调度结果进行计算可知,QSA对HEFT的平均优化率为38.76%,对HSIP的平均优化率为29.49%,对文献[11]所提算法的平均优化率为24.44%。

实验4随机生成一组处理器数为3,任务数为20、40、60的随机DAG。计算得到结果对比如图8所示,计算得到QSA算法相对于对比算法的优化率。

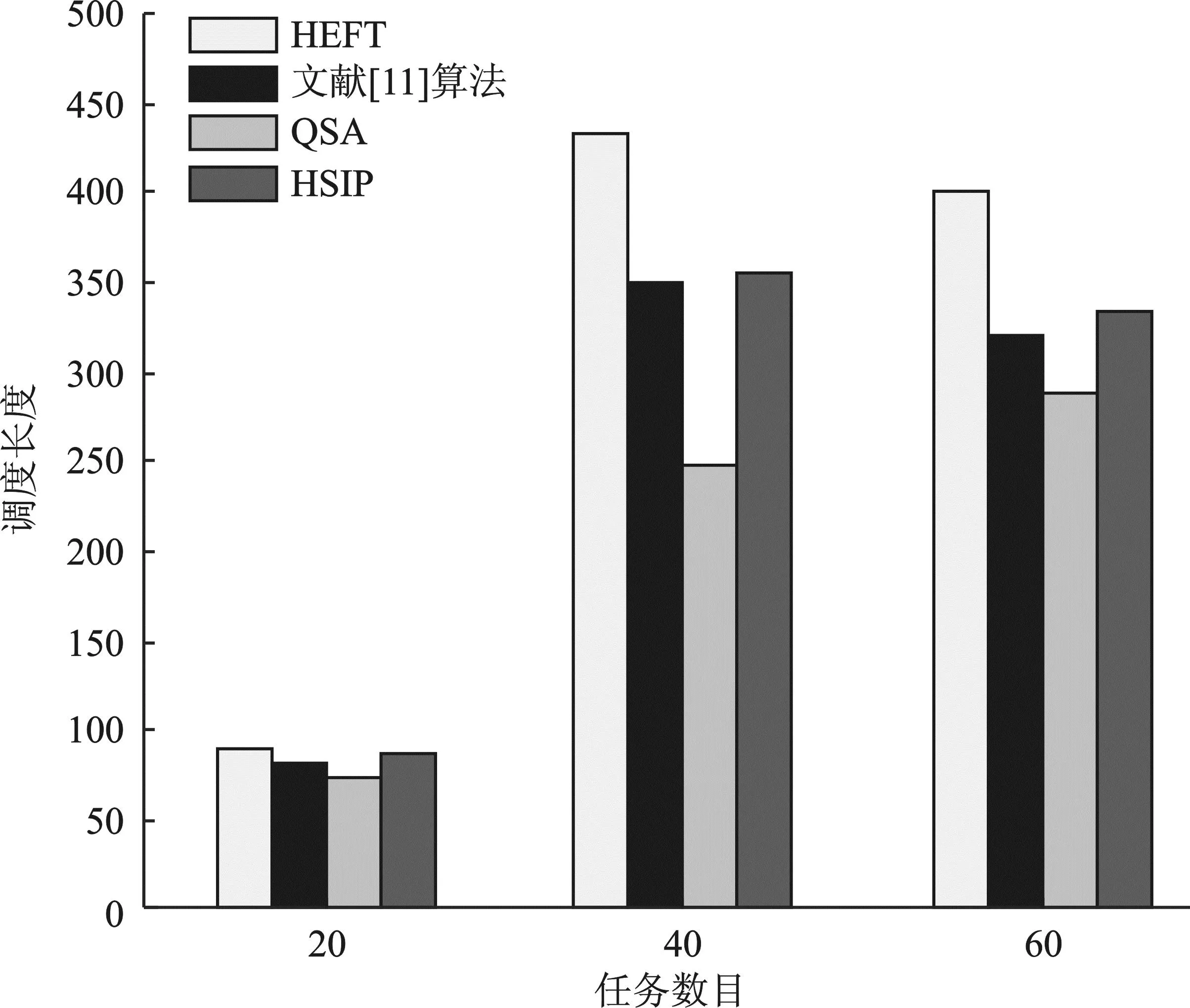
图8 实验4调度长度对比Figure 8. Comparison of scheduling length in experiment four

从调度结果可以看出,QSA算法的调度长度均优于HEFT和文献[11]所提算法,对调度结果进行计算可知,QSA对HEFT的平均优化率为29.52%,对HSIP的平均优化率为19.82%,对文献[11]所提算法的平均优化率为16.22%。

从以上两组实验中看出,在任务数相同处理器数变化和处理器数相同任务数变化的两种情况下,QSA算法的调度长度均达到了预期的优化效果,证明了该算法的可靠性。

4 结束语

针对异构信号处理平台中已有调度算法对现代信号处理应用的调度长度较大导致应用的实时性下降问题,本文提出QSA算法。该算法采用任务优先级分流排序策略,对通信密集型任务和计算密集型任务制定不同的优先级计算方法。采用量子比特对任务分配方案进行编码,通过将量子比特映射为二进制比特过程跳出局部最优解。根据适度函数值大小,通过量子旋转门更新量子比特,朝最小调度长度方向不断迭代优化。考虑入口任务的关键性,将入口任务按照最小计算开销原则分配,并利用任务复制思想降低任务间通信开销,取得最小调度长度。通过仿真实验可知,QSA算法能够有效提高信号处理应用的实时性。