Bi2(Se0.53Te0.47)3纳米线的制备及其圆偏振光致电流效应

冯世尊, 俞金玲

(福州大学物理与信息工程学院, 福建 福州 350108)

0 引言

拓扑绝缘体是一类新型的量子材料, 它的独特点在于其体态是普通绝缘体, 即费米能级处在导带和价带之间, 存在一定大小的能隙, 但其表面态却是导体, 即费米能级处存在一定的电子态密度[1]. 拓扑绝缘体特殊的能带结构会引起特殊的光学响应和基于圆偏振光电流效应的自旋极化电流调制. 拓扑绝缘体特殊的表面态是受时间反演对称性保护的, 大的自旋轨道耦合会抑制电子的背向散射, 从而降低了其表面态对表面杂质和缺陷的敏感性. 此外, 拓扑绝缘体的表面态是自旋动量锁定的, 会产生强大的自旋极化, 这使得此类材料在自旋电子学领域的研究具有重要意义. Bi2Se3、 Bi2Te3、 Sb2Te3及其合金属于第三代强三维拓扑绝缘体, 由于其能带结构简单、 材料性能稳定且易于制备, 现已成为拓扑绝缘体材料体系中的研究热点[2].

圆偏振光致电流效应(circular photogalvanic effect, CPGE)电流是一种新型的光电流技术, 是研究自旋流的一种有效手段, 它是由光子的角动量传递给自由运动的载流子而产生的电流. 由于三维拓扑绝缘体的体态属于D3d对称性, 表面态属于C3v对称性, 它们的表面态会产生CPGE电流(ICPGE)而体态不会. 因此, 可以利用CPGE电流来研究三维拓扑绝缘体的表面态. 与其他纳米结构相比, 纳米线材料具有更高的比表面积, 其表面态占据主导地位. 因此, 纳米线是研究三维拓扑绝缘体表面态的理想材料之一[3-4]. 纳米线的制备方法有很多种, 大致可分为机械剥离法、 溶剂热合成法、 分子束外延法、 化学气相沉积法、 物理气相沉积法和磁控溅射法等. 其中, 化学气相沉积法因其成本低廉、 操作简单、 制备的晶体质量高, 被广泛应用于低维纳米材料的制备中.

Meyer等[5]于2020年发现Bi2Se3纳米线中的CPGE电流, 证实了拓扑绝缘体纳米器件中产生CPGE电流的可能性. Li等[6]于2022年对三元拓扑绝缘体Bi2(Te0.23Se0.77)3纳米线的CPGE电流进行了测试, 发现相比于二元Bi2Se3纳米线, 三元Bi2(Te0.23Se0.77)3纳米线的CPGE电流更大, 这是因为Te元素的引入可使费米能级离狄拉克点更近, 减小体态的散射, 从而增大了CPGE电流. 目前关于拓扑绝缘体纳米线CPGE电流的研究较少, 通过调节元素组分是否能够进一步提高CPGE电流, 还需要进一步的研究分析.

本研究利用化学气相沉积(chemical vapor deposition, CVD)法制备三元拓扑绝缘体Bi2(Se0.53Te0.47)3纳米线, 并测试其CPGE电流. 对比激光入射面垂直和平行于纳米线时的CPGE电流, 以揭示纳米线表面态和体态对CPGE电流的贡献. 研究CPGE电流随入射角的变化规律和Te元素在费米能级调节中的作用.

1 实验材料与方法

实验装置如图1所示. 本研究使用的拓扑绝缘体Bi2(Se0.53Te0.47)3纳米线用CVD法制备, 制备原理如图1(a)所示. 将Bi2Te3粉末和Bi2Se3粉末作为原料, 二者均购于阿法埃莎(中国)化学有限公司, 纯度均为99.999%. 将p型(111)面的Si作为生长衬底. 实验前, 需要在衬底表面涂敷一层金纳米颗粒作为催化剂. 将原料和衬底放入石英舟并推入石英管中进行纳米线生长. 原料Bi2Te3粉末和Bi2Se3粉末分别需要10和30 mg, 生长温度为530 ℃, 升温时间为30 min, 保持时间为120 min, 气流量为30 mL·min-1, 气压为25 Pa. 生长后的纳米线需要转移到干净的SiO2/Si衬底上, 再对转移之后的纳米线进行光刻和蒸镀等操作, 以制作出金电极. 最后, 将其放入杜瓦瓶中进行自旋光电流的测试.

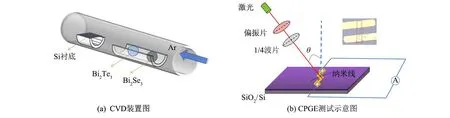
图1 实验装置示意图Fig.1 Schematic diagram of experimental equipment

图1(b)是CPGE电流测试示意图, 右上角插图为纳米线器件的光学显微镜图片. 实验中采用的激光波长为1 064 nm, 激光光强呈高斯分布, 光斑大小约为0.5 mm. 激光通过偏振片和1/4波片以入射角θ照射在样品上, 激光激发产生的光电流通过两个电极进行收集, 然后由一个前置放大器和一个锁相放大器进行放大. 测得的光电流信号可以利用下式进行拟合[7-8], 求得总的光电流(Itotal), 从而提取出CPGE电流. 即

Itotal=Csin 2θ1+L1sin 4θ1+L2cos 4θ1+j0

(1)

式中:θ1是1/4波片的角度;C为圆偏振光致电流信号幅值;L1和L2为线偏振光致电流幅值;j0为由光伏效应和登伯效应引起的背景电流信号[9-11].

图1(c)和(d)分别为激光入射面垂直纳米线和平行纳米线的原理图. 激光入射面如图中的白色透明平面所示, 黑色的线表示纳米线.

2 实验结果与分析

图2(a)为Si衬底上生长纳米线的扫描电子显微镜(scanning electron microscopy, SEM)形貌图. 从图中可以看出, Si衬底上生长有很多杂乱无章排列的纳米线, 它们的长度从几微米到几十微米不等. 衬底上不仅有纳米线, 还有纳米片. 图2(b)为单根纳米线的SEM形貌图. 从图中可以看出, 纳米线的宽度大约在80～100 nm之间. 图2(c)是纳米线的X射线能谱(energy dispersive X-ray spectroscopy, EDS)图. 从图中可以看出, Te元素和Se元素在总元素中的原子百分比分别为23.24%和26.07%, 其总和共约50%, 他们各自占两种元素之和的比例分别为47%和53%, 所以制备的纳米线为Bi2(Se0.53Te0.47)3纳米线. 通过转移和光刻等工艺, 将表征好的Bi2(Se0.53Te0.47)3纳米线制备成3个纳米线光电器件, 并对它们的CPGE电流进行研究.

图2 纳米线的形貌和成分图Fig.2 Appearance images and element image of nanowires

光的偏振状态随着1/4波片转动呈现周期性变化, 在45°和225°时为左旋圆偏振光, 在135°和315°时为右旋圆偏振光. 图3(a)和(b)分别为激光入射面垂直于和平行于纳米线时, 当入射角为+30°时的光电流(I光电流)随着1/4波片转角(θ1)的变化曲线. 图中的黑色方形为总的自旋光电流扣除背景电流(j0)后的光电流数据, 黑色曲线为利用公式(1)拟合的曲线, 红色曲线是拟合后的CPGE电流, 绿色和蓝色曲线是拟合得到的线偏振光致电流效应(linear photogalvanic effect, LPGE)电流. 图3(a)中拟合得到的C值为0.024 21 nA,L1值为-0.002 68 nA,L2值为-0.008 99 nA. 图3(b)中拟合得到的C值为0.004 55 nA,L1值为0.002 98 nA,L2值为-0.018 23 nA. 激光入射面垂直于纳米线时测得的CPGE电流比激光入射面平行于纳米线时大, 这表明测得的CPGE电流主要来自纳米线的表面态. 具体来说, 因为纳米线表面态是自旋动量锁定的, 当圆偏振光入射面垂直于纳米线, 即x-z平面时, 将产生沿x方向的自旋极化载流子. 由于自旋动量锁定效应, 沿x自旋方向的自旋极化载流子将具有y方向动量, 导致沿y方向产生较大的CPGE电流. 如果圆偏振光入射面平行于纳米线, 即y-z平面, 将产生沿y方向的自旋偏振载流子, 由于自旋动量锁定效应, 自旋极化载流子将具有x方向动量, 不会产生沿y方向流动的CPGE电流. 此时, 在实验中观测到沿y方向流动的少量CPGE电流. 这可能是因为摆放的纳米线并未完全与圆偏振光入射面平行, 存在一定的夹角, 导致沿x方向产生很少的自旋极化载流子. 由于自旋动量锁定效应, 这些少数沿x方向的自旋极化载流子具有y方向的动量, 导致沿y方向产生很小的CPGE电流[6].

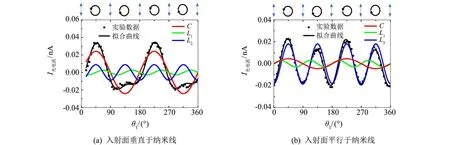
图3 光电流随1/4波片转动角度的变化曲线Fig.3 Change curves of the photocurrent with rotation angle of the 1/4 wave plate

图4(a)和(b)是在1 064 nm激光激发下, 当激光入射面分别垂直和平行于纳米线时的CPGE电流随着入射角(θ)的变化曲线. 黑色方形为实验测得的数据, 红色曲线为拟合曲线. 实验时的光功率为100 mW, 入射角从-30°到+30°, 步长为10°.

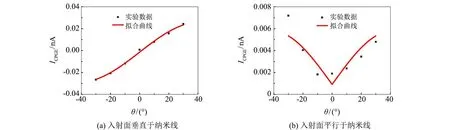
图4 CPGE电流随入射角的变化曲线Fig.4 Change curves of CPGE current with incident angle

当激光入射面垂直于纳米线时, CPGE电流随着入射角的增大而增大, 并且随着入射角的反号而反号, 是入射角的奇函数. 这种现象说明CPGE电流主要来自于拓扑绝缘体表面态, 它们的对称性属于C3v. 此时, CPGE电流随着入射角的变化曲线可以描述为

(2)

式中:A是一个拟合参数, 它的值与样品的自旋轨道耦合系数成正比;n是样品的折射率, 这里取其值为5.45;θ是入射角.

当激光入射面平行于纳米线时, CPGE电流随着入射角的增大而增大, 但不随入射角的反号而反号, 是入射角的偶函数. 特别需要注意的是, 理论上CPGE电流在0°时应该为0, 但实际测得的CPGE电流并不为0. 这可能是因为圆偏振光还激发六角翘曲上的平面外自旋电子, 从而产生平面外自旋极化电流, 实际所测得的电流是CPGE电流和平面外自旋极化电流的叠加[12-13].

当激光入射面平行于纳米线时, CPGE电流随着入射角的变化曲线可以描述为

(3)

式中:Js是圆偏振光激发纳米线能带中的六角翘曲效应所产生的自旋极化电流.

在室温为300 K、 入射角为+30°、 激光功率为100 mW时, 3个纳米线器件拟合得到的C值分别为0.024 21、 0.025 32、 0.024 30 nA, 测试得到的C值变化很小, 比较稳定. 同时在70 mV偏压下测量1个纳米线器件的光电导电流, 其值为5.02 nA. 在相同条件下, Li等[6]报导的Bi2(Te0.23Se0.77)3纳米线的C值约为0.010 nA, 光电导电流约为0.48 nA. 通过与上述文献中Bi2(Te0.23Se0.77)3纳米线的CPGE电流作对比, 发现本研究Bi2(Se0.53Te0.47)3纳米线的CPGE电流是文献报导值的2倍以上. 此外, Bi2(Se0.53Te0.47)3纳米线的光电导电流值比Bi2(Te0.23Se0.77)3纳米线大一个数量级. 这可能是由于光电导电流与纳米线中的载流子浓度有关, Te元素占比的增加使得纳米线中载流子复合率降低. 另外, 随着Te元素含量的增加, 费米能级更靠近狄拉克点, 抑制体态电子对表面光生自旋极化载流子的散射. 这两者共同作用, 从而增大了纳米线中的CPGE电流.

图5是CPGE电流随着激光功率(P)的变化曲线. 实验中, 通过转动衰减片来改变激光功率, 光功率从20 mW变到100 mW, 步长为10 mW, 激光入射角为+30°, 测量温度为室温. 图中的黑色方形表示实验数据, 蓝色实线为线性拟合结果. 从图中可以明显看出, CPGE电流随着光功率的增大而增大, 呈线性关系. 这可以用如下的公式来解释, 即x方向的CPGE电流可表示为

ICPGE, x=γxyRcircηGêy

(4)

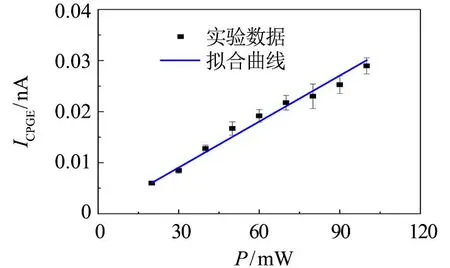
图5 CPGE电流随激光功率的变化曲线Fig.5 Change curve of CPGE current with laser power

式中:γxy是一个正比于体系自旋轨道耦合系数的常数;Rcirc为入射光圆偏振度;η为光吸收系数;G是载流子浓度; êy为入射光在纳米线中的传播方向在y方向的投影. 随着光功率的增大, 光生载流子浓度(G)随之增大, 所以CPGE电流随着功率线性增加.

3 结语

利用CVD法制备Bi2(Se0.53Te0.47)3纳米线, 研究其CPGE电流. 实验发现激光入射面垂直于纳米线时的CPGE电流大于激光入射面平行于纳米线时的值, 这是由纳米线表面态的自旋动量锁定效应所导致的. 通过测试CPGE电流与入射角之间的关系, 发现激光入射面垂直于纳米线时的CPGE电流是入射角的奇函数, 平行于纳米线时的CPGE电流是入射角的偶函数. 当激光垂直入射时, CPGE电流不为0, 这可能是由纳米线能带的六角翘曲效应导致的. 将本研究中变角度的CPGE电流与文献值进行对比, 发现随着Te元素的增加, CPGE电流增大. 这可能是因为Te元素的增加使得费米能级更靠近狄拉克点, 抑制体态电子对表面光生自旋极化载流子的散射, 同时降低了纳米线中的载流子复合率, 从而使得纳米线的CPGE电流增加. 本研究提高了三元拓扑绝缘体Bi2(SexTe1-x)3纳米线的圆偏振光响应度, 使其成为光电探测器的潜在应用平台.