四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)的极小范数最小二乘Toeplitz解
石俊岭, 李 莹, 王 涛, 张东惠, 邱 新
(聊城大学 数学科学学院, 山东 聊城 252000)
矩阵方程是数值代数领域的重要研究内容之一,而四元数及四元数矩阵在彩色图像处理、计算机技术、动力学等领域具有重要的应用[1-3],因而四元数矩阵方程也成为矩阵方程中热门的研究课题.然而四元数乘法的不可交换性使得四元数矩阵方程的研究相比实矩阵方程更为复杂.因此,许多学者提出一些同构关系,将四元数矩阵方程问题转化为等价的实矩阵方程问题解决,从而极大降低问题求解的复杂程度.例如,丁文旭等[4]提出一种四元数矩阵的实向量表示方法,并给出求解四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)的极小范数Hermitian解的有效方法.王秀平等[5]基于四元数矩阵实表示,提出求解四元数矩阵方程(AXB,CXD)=(E,F)的极小范数最小二乘Hermitian解的有效方法.本文将基于四元数矩阵实表示,结合矩阵的H-表示以及矩阵半张量积,提出一种求解四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)的极小范数最小二乘Toeplitz解的有效方法,并给出数值算法与算例,从而验证该方法的有效性.具体问题如下:
问题1设Ai∈Qm×n,Bi∈Qn×p,Ci∈Qm×p(i=1,…,k),记
寻找XS∈S满足:
XS称为四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)的极小范数最小二乘Toeplitz解.

1 预备知识
1843年,爱尔兰数学家W.R.Hamilton提出了四元数的概念,它是复数的不可交换延伸,是实数域上的四维非交换结合代数.
定义1[6]定义四元数为
a=a1+a2i+a3j+a4k
其中:a1,a2,a3,a4∈R.且i,j,k满足i2=j2=k2=-1,ij=-ji=k,ki=-ik=j,jk=-kj=i.


定义2[5]对于四元数矩阵A=A1+A2i+A3j+A4k∈Qm×n,称矩阵AR为四元数矩阵的实表示矩阵
由实表示矩阵的结构可以看出,实表示矩阵与实表示矩阵的第一列块一一对应,记实表示矩阵第一列块为
四元数矩阵的(F)范数为
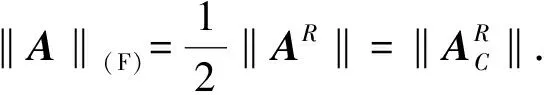
四元数矩阵的实表示具有以下性质:
引理1[5]设A,B∈Qm×n,C∈Qn×p,则有
2) (A+B)R=AR+BR,(kA)R=kAR,(AC)R=ARCR.
本文的重要研究工具之一为矩阵半张量积,矩阵半张量积是现代矩阵理论的重要内容之一,它突破了经典矩阵乘法维数的限制,是经典矩阵乘法的推广.这种推广不仅保持了经典矩阵乘法所有的基本性质,并且突破了经典矩阵乘法中一些不可逾越的问题,如经典矩阵乘法无交换性,经典矩阵乘法无法处理高阶多线性函数等,具有十分重要的现实意义,现已广泛应用到众多领域[7-11].矩阵半张量积的定义如下:
定义3[12]设A∈Qm×n,B∈Qp×q,n与p的最小公倍数为t=lcm(n,p),定义A与B的矩阵半张量积为
A▷B=(A⊗It/n)(B⊗It/p)
显然,当n=p时,A与B的半张量积即为A与B的经典矩阵乘积.故矩阵半张量积是经典矩阵乘法的推广.
定义4[12]设A=(aij)∈Qm×n,定义A的列排式为
Vc(A)=(a11,…,am1,a12,…,am2,…,a1n,…,amn)T
A的行排式为
Vr(A)=(a11,…,a1n,a21,…,a2n,…,am1,…,amn)T
定义5[12]定义mn维换位矩阵
利用换位矩阵,可以实现四元数矩阵A列排式与行排式的转化.
引理2[12]1) 设A∈Qm×n,则
W[m,n]Vr(A)=Vc(A),W[n,m]Vc(A)=Vr(A)
2) 设A∈Qm×n,则
W[m,p]▷A▷W[p,n]=Ip⊗A
利用定义3、定义4、定义5以及引理2进一步研究四元数矩阵行排式及列排式之间的关系.
定理1设A=(aij)∈Qm×n,X=(xij)∈Qn×q,Y∈Qp×m, 则
2)Vc(AX)=(Iq⊗A)Vc(X),Vr(AX)=A▷Vr(X).
证明1) 记A=(α1,α2,…,αn),Y=(y1,y2,…,ym), 则

2) 记xi=(x1i,…,xni)T,(i=1,…,q).由1)的结论可得
令xj=(xj1,…,xjq)T,(j=1,…,n),同理由1)的结论可得
(A⊗Iq)Vr(X)=A▷Vr(X)
引理3[13]设A∈Rm×n,b∈Rm,则不相容线性方程组Ax=b最小二乘解的通式为x=A†b+(In-A†A)y,其中y∈Rn是任意的.
引理4[13]设A∈Rm×n,b∈Rm,则线性方程组Ax=b有解的充分必要条件为AA†b=b.此时,Ax=b的通解为x=A†b+(In-A†A)y,其中y∈Rn是任意的.
2 矩阵的H-表示
为了降低问题求解的复杂程度,首先介绍特殊矩阵的H-表示,针对实数域上Toeplitz矩阵,对其进行元素个数的缩减并给出实数域上Toeplitz矩阵H-表示方法.
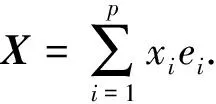

对于实数域上的Toeplitz矩阵
可根据其结构特点,利用H-表示提取有效元素,进行元素个数的缩减,从而降低求解问题的复杂程度.

{e0,e1,…,en-1,e-1,…,e-(n-1)}
其中

由标准基底的选定可得实数域上Toeplitz矩阵的H-表示矩阵Hn如下:
3 问题1的代数解
利用实数域上Toeplitz矩阵的H-表示方法、矩阵半张量积、四元数矩阵的实表示矩阵等研究问题1的代数解,从而得到定理2及其推论.

则问题1中的集合可以表示为
四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)极小范数最小二乘Toeplitz解XS满足:
(1)
证明由四元数矩阵的(F)范数的性质可得
故问题1中的集合S可以表示为

即
其中:y∈R8n-4是任意的,故问题1的集合为

从而四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)极小范数最小二乘Toeplitz解XS满足:
推论1四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)有Toeplitz解的充要条件为
(MM†-I4kmp)N=O
且方程的Toeplitz解X满足:
其中:y∈R8n-4是任意的.
极小范数Toeplitz解Xm满足:
证明四元数矩阵方程(A1XB1,…,AkXBk)=(C1,…,Ck)存在Toeplitz解等价于
其中:y∈R8n-4是任意的.
故此时四元数矩阵方程的Toeplitz解X满足:
其中:y∈R8n-4是任意的.
且极小范数Toeplitz解Xm满足:
4 数值算法及算例
根据式(1)以及推论1的结论给出问题1的数值算法,并给出两个算例分别从误差和计算时间两个方面验证该方法的有效性.
算法1(问题1的数值算法)
1) 输入Ai∈Qm×n,Bi∈Qn×p,Ci∈Qm×p,输出U,V,N,G,G′.
2) 输入Hn,输出W,M.
3) 根据式(1)输出问题1的极小范数最小二乘Toeplitz解.

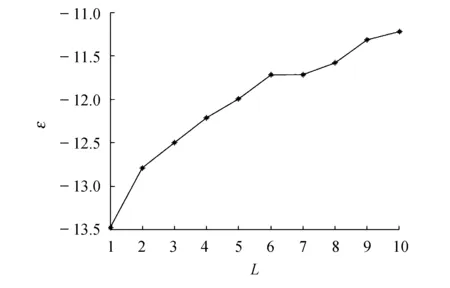
图1 不同矩阵维数下误差的数量级 Fig.1 The order of magnitude of error with different matrix dimensions
由图1知‖X*-X‖(F)<10-11,故由算法1所得到的问题1的解的精确程度是可以保障的.
算例2在MATLAB中随机生成四元数矩阵A∈Qm×n,B∈Qn×p,C∈Qm×p,(其中取m=n=p=10L,L=1,2,…,7),分别通过算法1、文献[4]中的实向量表示方法与文献[5]中实表示方法计算四元数矩阵方程AXB=C极小范数最小二乘Toeplitz解,将三种方法所耗费的计算时间进行对比,由于文献[4]中的实向量表示方法在求解过程中所需储存量过大,在计算规模较大的问题时,其计算时间比另外两种方法长,故只需对另外两种方法所耗费的计算时间进行对比,见表1所列.

表1 不同矩阵维数下各种方法所需计算时间
由表1可以看出,与文献[5]中的实表示方法相比,随着矩阵维数的增大,本文提出的方法所需计算时间优势越来越大.
综上所述,算法1不仅结果十分精确而且在计算时间上具有相当大的优势,故本文针对问题1的求解方法是十分有效的.
5 结论
本文基于四元数矩阵实表示,结合矩阵半张量积与矩阵H-表示,提出了求解四元数线性系统极小范数最小二乘Toeplitz解的有效方法.利用矩阵H-表示,提取有效元素,大大降低了问题求解的复杂度,在问题求解过程中具有十分重要的作用.该问题的求解方法可应用于其他线性系统特殊解的求解问题中,具有十分重要的意义.

