有关奇亏完全数的一些刻画
张四保
(1. 喀什大学 数学与统计学院, 新疆 喀什 844000; 2. 喀什大学 现代数学及其应用研究中心, 新疆 喀什 844000)
对于正整数n,令函数σ(n)表示n的所有正因数的和函数.在数论中,存在与函数σ(n)相关的众多问题.若一个正整数n满足σ(n)=2n,则n被称之为完全数.到目前为止仅发现51个偶完全数,而尚未发现奇完全数.奇完全数的存在性是数论中长期未能解决的著名难题[1].有关奇完全数的最新研究可见文献[2-4].若一个正整数n满足σ(n)=2n+d,则n被称之为盈度为d的盈完全数;若一个正整数n满足σ(n)=2n-d,则n被称之为亏度为d的亏完全数,这里的d都是正整数n的真因数.盈度为d的盈完全数与亏度为d的亏完全数备受数论爱好者的关注,与此相关有很多未解决的问题[5].
对于盈完全数的研究可见文献[6-7].同样,对于奇亏完全数存在性问题有着不少的研究,获得了很丰富的研究成果.Tang等[8]讨论了素因数个数不超过2个的亏完全数的存在性问题,刻画了其结构;冯敏[5]与Tang等[9]讨论了具有3个互异素因数的奇亏完全数的存在性问题,证明了不存在具有3个互异素因数的奇亏完全数;张四保等[10]、Cui等[11]及马小艳等[12]讨论具有4个互异素因数的奇亏完全数的存在性问题,各自给出了具有4个互异素因数的奇亏完全数的某些刻画;张四保[13]讨论具有5个互异素因数的奇亏完全数的存在性问题,给出了具有5个互异素因数的奇亏完全数的某些刻画.本文在相关文献的研究基础上,继续讨论具有5个互异素因数的奇亏完全数的存在性问题,给出具有5个互异素因数的奇亏完全数的一些刻画.
1 几个基本引理



得出矛盾.
2 结论及其证明

证明此时,若q4≥53,则有
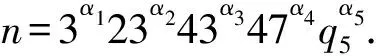
得出矛盾.因而q5∈{53,59,61}.

得出矛盾.
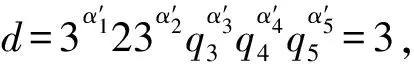
(1)


令
由式(1)可得
F1(α1,α2,α3,α4,α5)=G1(α1,α2,α3,α4,α5)
(2)
当α1≥6,q5=53时,有
因而有F1(α1,α2,α3,α4,α5)>G1(α1,α2,α3,α4,α5),这与式(2)不符.
当α1≥6,q5=59时,有
因而有F1(α1,α2,α3,α4,α5)>G1(α1,α2,α3,α4,α5),这与式(2)不符.
当α1≥6,q5=61时,有
F1(α1,α2,α3,α4,α5)=
G1(α1,α2,α3,α4,α5)=
0.999 342…
因而有F1(α1,α2,α3,α4,α5)>G1(α1,α2,α3,α4,α5),这与式(2)不符.
定理1证毕.
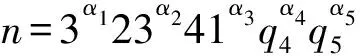
1) 当q4=43时,若q5∈{47,53,59,61,67,71,73},则n不是奇亏完全数;
2) 当q4=47,则n不是奇亏完全数.
证明此时,若q4≥53,则有
得出矛盾.因而q4∈{43,47}.

得出矛盾.因而q5∈{47,53,59,61,67,71,73,79}.

得出矛盾.

(3)


令
由式(3)可得
F2(α1,α2,α3,α4,α5)=G2(α1,α2,α3,α4,α5)
(4)
当α1≥6,q5=47时,有
因而有F2(α1,α2,α3,α4,α5)>G2(α1,α2,α3,α4,α5),这与式(4)不符.
当α1≥6,q5=53时,有
因而有F2(α1,α2,α3,α4,α5)>G2(α1,α2,α3,α4,α5),这与式(4)不符.
当α1≥6,q5=59时,有
因而有F2(α1,α2,α3,α4,α5)>G2(α1,α2,α3,α4,α5),这与式(4)不符.
当α1≥6,q5=61时,有
因而有F2(α1,α2,α3,α4,α5)>G2(α1,α2,α3,α4,α5),这与式(4)不符.
当α1≥6,q5=67时,有
因而有F2(α1,α2,α3,α4,α5)>G2(α1,α2,α3,α4,α5),这与式(4)不符.
当α1≥6,q5=71时,有
因而有F2(α1,α2,α3,α4,α5)>G2(α1,α2,α3,α4,α5),这与式(4)不符.
当α1≥6,q5=73时,有
因而有F2(α1,α2,α3,α4,α5)>G2(α1,α2,α3,α4,α5),这与式(4)不符.

得出矛盾.因而q5∈{53,59,61,67}.

得出矛盾.

(5)


令
由式(5)可得
F3(α1,α2,α3,α4,α5)=G3(α1,α2,α3,α4,α5)
(6)
当α1≥6,q5=53时,有
因而有F3(α1,α2,α3,α4,α5)>G3(α1,α2,α3,α4,α5),这与式(6)不符.
当α1≥6,q5=59时,有
因而有F3(α1,α2,α3,α4,α5)>G3(α1,α2,α3,α4,α5),这与式(6)不符.
当α1≥6,q5=61时,有
因而有F3(α1,α2,α3,α4,α5)>G3(α1,α2,α3,α4,α5),这与式(6)不符.
当α1=6,q5=67时,有
σ(3α1)=1 093|σ(3α123α241α347α467α5)
由式(5)可得1 093|5×3α1-123α241α347α467α5,这是矛盾的式子.
当α1=8,q5=67时,有
σ(3α1)=9 841=13×757|σ(3α123α241α347α467α5)
由式(5)可得13×757|5×3α1-123α241α347α467α5,这是矛盾的式子.
当α1≥10,q5=67时,
F3(α1,α2,α3,α4,α5)=
G3(α1,α2,α3,α4,α5)=
0.999 672…
因而有F3(α1,α2,α3,α4,α5)>G3(α1,α2,α3,α4,α5),这与式(6)不符.
定理2证毕.

1) 当q4=41时,若q5∈{43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109},则n不是奇亏完全数;
2) 当q4∈{43,47,53,59}时,n不是奇亏完全数.
证明此时,若q4≥61,则有
得出矛盾.因而q4∈{41,43,47,53,59}.

得出矛盾.因而q5∈{43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113}.

得出矛盾.

(7)


令
由式(7)可得
F4(α1,α2,α3,α4,α5)=G4(α1,α2,α3,α4,α5)
(8)
当α1≥6,q5∈{43,47,53,59,61,67,71,73,79,83,89,97,101,103}时,经计算有F4(α1,α2,α3,α4,α5)>G4(α1,α2,α3,α4,α5)这与式(8)不符.
当α1=6,q5=107时,有
σ(3α1)=1 093|σ(3α123α237α341α4107α5)
由式(7)可得1 093|5×3α1-123α237α341α4107α5,这是矛盾的式子.
当α1=8,q5=107时,有
σ(3α1)=9 841=13×757|σ(3α123α237α341α4107α5)
由式(7)可得13×757|5×3α1-123α237α341α4107α5,这是矛盾的式子.
当α1≥10,q5=107时,有
因而有F4(α1,α2,α3,α4,α5)>G4(α1,α2,α3,α4,α5),这与式(8)不符.
当α1=6,q5=109时,有
σ(3α1)=1 093|σ(3α123α237α341α4109α5)
由式(7)可得1 093|5×3α1-123α237α341α4109α5,这是矛盾的式子.
当α1=8,q5=109时,有
σ(3α1)=9 841=13×757|σ(3α123α237α341α4109α5)
由式(7)可得13×757|5×3α1-123α237α341α4109α5,这是矛盾的式子.
当α1≥10,q5=109时,有
因而有F4(α1,α2,α3,α4,α5)>G4(α1,α2,α3,α4,α5),这与式(8)不符.
得出矛盾.因而q5∈{47,53,59,61,67,71,73,79,83,89,97}.

得出矛盾.

(9)


令
由式(9)可得
F5(α1,α2,α3,α4,α5)=G5(α1,α2,α3,α4,α5)
(10)
当α1≥6,q5∈{47,53,59,61,67,71,73,79,83,89}时,经计算有
F5(α1,α2,α3,α4,α5)>G5(α1,α2,α3,α4,α5)
这与式(10)不符.
当α1=6,q5=97时,有
σ(3α1)=1 093|σ(3α123α237α343α497α5)
由式(9)可得1 093|5×3α1-123α237α343α497α5,这是矛盾的式子.
当α1=8,q5=97时,有
σ(3α1)=9 841=13×757|σ(3α123α237α343α497α5)
由式(9)可得13×757|5×3α1-123α237α343α497α5,这是矛盾的式子.
当α1≥10,q5=97时,有

因而有F5(α1,α2,α3,α4,α5)>G5(α1,α2,α3,α4,α5),这与式(10)不符.

得出矛盾.因而q5∈{53,59,61,67,71,73,79,83}.

得出矛盾.

(11)
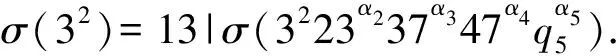

令
由式(11)可得
F6(α1,α2,α3,α4,α5)=G6(α1,α2,α3,α4,α5)
(12)
当α1≥6,q5∈{53,59,61,67,71,73,79}时,经计算有F6(α1,α2,α3,α4,α5)>G6(α1,α2,α3,α4,α5),这与式(12)不符.
当α1=6,q5=83时,有
σ(3α1)=1093|σ(3α123α237α347α483α5)
由式(11)可得1 093|5×3α1-123α237α347α483α5,这是矛盾的式子.
当α1=8,q5=83时,有
σ(3α1)=9 841=13×757|σ(3α123α237α347α483α5)
由式(11)可得13×757|5×3α1-123α237α347α483α5,这是矛盾的式子.
当α1=10,q5=83时,有σ(3α1)=88 573=23×3 851|σ(3α123α237α347α483α5),由式(11)可得23×3 851|5×3α1-123α237α347α483α5,这是矛盾的式子.
当α1≥12,q5=83时,有
因而有F6(α1,α2,α3,α4,α5)>G6(α1,α2,α3,α4,α5),这与式(12)不符.

得出矛盾.因而q5∈{59,61,67}.

得出矛盾.

(13)
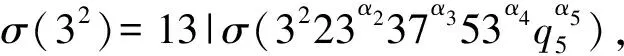

令
由式(13)可得
F7(α1,α2,α3,α4,α5)=G7(α1,α2,α3,α4,α5)
(14)
当α1≥6,q5=59时,有
因而有F7(α1,α2,α3,α4,α5)>G7(α1,α2,α3,α4,α5),这与式(14)不符.
当α1≥6,q5=61时,有
因而有F7(α1,α2,α3,α4,α5)>G7(α1,α2,α3,α4,α5),这与式(14)不符.
当α1≥6,q5=67时,有
因而有F7(α1,α2,α3,α4,α5)>G7(α1,α2,α3,α4,α5),这与式(14)不符.

得出矛盾.因而q5=61.
若d=3α′123α′237α′359α′461α′5≥9,其中0≤αi≤α′i,i=1,2,…,5,则有
得出矛盾.
若d=3α′123α′237α′359α′461α′5=3,则α1-α′1=1,αi=α′i,i=2,3,4,5,则由奇亏完全数的关系式σ(n)=2n-d可得
σ(3α123α237α359α461α5)=5×3α1-123α237α359α461α5
(15)
当α1=2时,σ(32)=13|σ(3223α237α359α461α5),由式(15)可得13|5×3α1-123α237α359α461α5,这是矛盾的式子.
当α1=4时,σ(34)=112|σ(3423α237α359α461α5),由式(15)可得112|5×3α1-123α237α359α461α5,这是矛盾的式子.
当α1=6时,
σ(36)=1 093|σ(3623α237α359α461α5)
由式(15)可得1 093|5×3α1-123α237α359α461α5,这是矛盾的式子.
当α1=8时,
σ(38)=9 841=13×757|σ(3823α237α359α461α5)
由式(15)可得13×757|5×3α1-123α237α359α461α5,这是矛盾的式子.
当α1=10时,
由式(15)可得
23×3 851|5×3α1-123α237α359α461α5
这是矛盾的式子.
令
由式(15)可得
F8(α1,α2,α3,α4,α5)=G8(α1,α2,α3,α4,α5)
(16)
当α1≥12,q5=61时,有
因而有F8(α1,α2,α3,α4,α5)>G8(α1,α2,α3,α4,α5),这与式(16)不符.
定理3证毕.
3 结语
对于奇亏完全数的研究,截至目前刻画了具有相异素因数个数不超过2的亏完全数的结构,以及明确了具有3个相异素因数的奇亏完全数的不存在性;同时也给出了具有多于3个相异素因数的奇亏完全数存在性的某些刻画,而未解决具有多于3个相异素因数的奇亏完全数存在性的问题.本文利用初等的方法,给出了3类具有5个相异素因数的奇正整数不是奇亏完全数的几个性质刻画,这将有助于讨论具有5个相异素因数的奇亏完全数存在性问题.

