人行桥在行人荷载激励下的非平稳随机响应

朱前坤, 曾 新

(兰州理工大学 防震减灾研究所, 甘肃 兰州 730050)

2000年,伦敦著名的千禧桥大幅振动事件成为人致桥梁振动的关键性标志,并引发学者对桥梁人致振动的广泛讨论[1].但很多学者研究人行桥人致振动问题时忽略了行人荷载的随机性,行人荷载是一个复杂的宽带随机过程,包含了行人内部不同步伐之间的作用随机性以及不同行人之间的作用随机性,随机性导致行人荷载将不同于以往按确定性考虑的情况[2].而且大多数荷载模型的预测和实际响应测量之间存在一定的差异,而差异的主要来源与行人和结构的相互作用以及行人行走的固有变异性有关[3-5].

学者对人行桥人致振动问题进行了深层次的研究,并提出了多种理论和模型,但都属于确定性分析方法,并没有考虑到行人荷载(行人内部以及行人之间的作用)的随机性[2].针对这一问题,林家浩等[6]提出了一种处理非平稳随机振动问题的高效精确的虚拟激励法,建立行人荷载作用下的人行桥振动响应,不需要蒙特卡罗模拟并考虑了行人内部以及行人之间的作用随机性.吕峰等[7]基于虚拟激励法和精细积分法,提出了一种研究桥梁随机动力特性的有限元精确高效算法.Caprani[8]提出了简单谱模型,应用虚拟激励法研究人行桥在不同行人激励下的非平稳振动响应,揭示了行人内部和行人之间的变异性.

虽然虚拟激励法在处理非平稳随机响应分析方面的计算效率较传统随机响应分析已有显著提高,但对于多自由度体系所需的计算量仍相当庞大,因此有必要进一步提高计算效率[9].Zhu等[10]、张琼等[11]将Eftekhari[12-13]提出的结合微分求解法和积分求积法用于研究结构在移动荷载作用下受迫振动问题的方法推广到人行荷载作用下人行桥振动响应的求解,通过与传统的振型叠加计算结果对比验证其高效性,并将其扩展到半刚性边界下的人行桥受行人荷载作用的振动响应问题[14].

基于以上研究,本文利用Caprani[8]提出的简单谱模型建立行人强迫函数的谱密度,结合微分求积法-虚拟激励法(DQ-PEM)求得人行桥在行人荷载激励下的非平稳随机响应.基于具体工程算例验证本文方法的准确性和高效性,并分析半刚性人行桥在行人荷载下作用下的非平稳随机响应问题,讨论不同速度和不同约束条件等因素对人行桥随机振动的影响.

1 行人荷载的谱模型

一般情况而言, 按照傅里叶级数的表达式, 人行激励作用可以由不同频率成分的简谐波激励合成, 并且这些频率与人行走的步频成正整数倍的关系.当人行走的步频与结构的固有频率接近或相等时, 会引起共振效应[15].

行走所产生的垂直荷载通常是由傅里叶级数的形式给出:

(1)

式中:ηi为第i次谐波的傅里叶系数,表示该谐波的动力因子(DLF),其值随谐波频率变化而变化,表1为相关值.

表1 文献中的一些动力因子(DLFs)

Brownjohn等[4]提出的谱模型中频谱只围绕每个谐波定义,而高次谐波则频谱存在许多重叠且无明确的解释.Caprani[8]提出的简单谱模型( Sim-SM)解决了上述不足,Sim-SM可表示行人内部和行人之间的变异性,模型通过正态分布对每个谐波的DLF进行扩展,公式如下所示:

(2)

其中:ηi为文献[4]中的动力因子;φ(f)为正态概率密度分布;第i次波的均值μi=ifp.假定变异系数(CoV)的标准差为σi=μiCoV.在实际应用中,间隔宽度Δf的频率间隔离散数为m,则式(2)变为

(3)

其模型如图1所示.

图1 CoV为5%,步频fp =2 Hz时的简单谱模型Fig.1 Simple spectral model of intra-subject variation for 2 Hz pacing frequency assuming 5% CoV

考虑单个谐波时,行人群体诱导垂直力的功率谱密度(PSD)会比单个行人的PSD更宽,本质上对单个行人的PSD进行扰动,以至于表示行人群体的PSD时还能考虑到单个行人的可变性.假设自谱密度Sxx由M个点给出,采用Kernel密度估计的思想:

(4)

其中:K(·)在文献[17]中给出,在极限下,则有两个函数的卷积得到总体的PSD:

(5)

假设单个行人PSD的第i次谐波表示为高斯函数:

(6)

进一步假设每一个谐波都使用高斯函数:

(7)

其中:σk,i为第i次谐波的带宽(通常用h表示),利用两个高斯函数的卷积是一个高斯函数的优点,公式(6)变为

(8)

其中的参数表达式为

(9)

如果使用简单谱模型(Sim-SM)来描述单个行人,可通过公式(9)增加每个谐波的标准差,同时表示行人间与行人内部的可变性,代表人口的模型,其准确性取决于人口变异性和高斯假设的接近程度.

2 梁式结构下的虚拟激励法

2.1 简介

以往的非平稳随机振动问题,常常简化成平稳随机激励计算,或者采用很简化的非平稳模型表示,即使这样,其计算量依旧比相应的平稳随机振动庞大,计算过程也复杂得多,很难在实际工程中被应用.而虚拟激励法在处理非平稳随机振动问题就方便很多[18],该方法精确、高效,是应用非常方便的结构随机振动分析算法系列,其适用于结构受到单点或多点、平稳或非平稳、部分相干或完全相干的随机激励.虚拟激励法在处理平稳随机振动问题时将其转化成确定性时间历程分析,从而使计算高效、精确.Zhong[19]描述了虚拟激励法相对于传统方法的计算优势:完全二次组合(CQC)与平方和的平方根(SRSS),对于N个自由度的系统,CQC需要N2个复数乘法,SRSS需要N个复数乘法(但是对于具有紧密间隔模式的一些结构来说不太精确),而虚拟激励法只需要一个等式(10)并且是精确的.因此,虚拟激励法适合于具有大量自由度且频率间隔很近的系统.

PEM已应用于大型基础设施的一系列问题[20],而精细积分法[21]和PEM法已被作为解决稳随机响应问题准确而有效的方法.近年来,已有多名学者将PEM应用于移动荷载作用下的桥梁振动问题[22].最近,Caprani[23]将PIM应用于行人桥的振动问题,称为模态精确积分法(MPIM),与其他常用的计算人行桥振动响应和统计方法相比,MPIM被证明是非常有效和高精度的.

2.2 人行桥振动的MPIM法

为评估由行人内部和行人之间的变异性引起的非平稳随机响应,使用PIM-PEM方案.实施情况如下:

1) 利用前文介绍的简单谱模型建立行人强迫函数的谱密度;

2) 将频谱划分成宽度为Δω的N个频率点;

3) 对于每一个频率点执行以下步骤:

b. 虚拟激励为

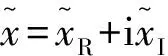
c. 当荷载在xk=vtk时所有时间步长响应为

通过对响应谱的积分,得到荷载k或时间t在每一个位置响应的均方值:

但该方法只适用于单自由度体系,无法对多自由度体系进行振动分析,需要利用DQ-PEM法求行人荷载下半刚性梁式结构的非平稳随机响应.

CT诊断：所有患者均采用我院的16层螺旋CT扫描机进行检查，扫描前将参数设为：扫描间距1mm，倾斜正负30°，层厚3mm。然后让患者保持仰卧位，对患者腰椎间隙部位进行扫描，为提高诊断检测的准确性，对间隙部位扫描3次。

2.3 行人荷载下人行桥的DQ-PEM法

微分求积-虚拟激励法(DQ-PEM)可用于求解人行桥在行人荷载下的非平稳随机响应问题.利用微分求积法将含Dirac函数的偏微分方程转化为不含Dirac函数的常微分方程,将Dirac函数视为非平稳函数,再结合虚拟激励法的思想求得其非平稳随机响应.

桥梁在行人荷载作用下响应是非平稳的[24-25],下式为桥梁受匀速移动荷载作用的振动控制方程[26-27]:

δ(x-vt)F(t)

(10)

式中:u(x,t)为桥梁的位移;v为随机荷载移动速度;δ(x-vt)为Dirac函数.

式(10)右边的荷载项可视为由Dirac函数与荷载F(t)组合而成的外激励均匀调制模型:

x(t)=δ(x-vt)F(t)

(11)

假设荷载F(t)的自谱密度为Sxx(ω),构造虚拟的移动确定性外部激励,可写为

(12)

其虚拟响应为

(13)

I(ω,t)为给定的确定性激励下结构的响应,可由DQ-IQ混合法求得.

(14)

为求得人行桥在行人荷载下的非平稳随机响应,采用DQ-PEM法,具体计算步骤如下:

1) 输入人行桥的各结构参数;

2) 使用简单谱模型(Sim-SM)建立行人强迫函数的谱密度;

3) 将频谱分成N频点,间隔为Δω,离散后每段外荷载频率ωn=nΔω;

5) 按式(14)求得每个ωn对应的响应的演变功率谱密度Syy(ωn,t);

3 工程算例

使用人行桥模型验证行人桥的谱问题,在计算匀速移动荷载作用下半刚性约束单跨梁式结构时采用图1所示的简单谱模型.人行桥的结构长L=30 m,线性质量为ρA=10×103kg/m,其抗弯刚度EI=7.48×1010N·m2,振型阻尼比为5%,其阻尼系数为c≈3.00×104N/(m·s).假设移动随机荷载类型为行人荷载,行人被认为以步频fp=2 Hz匀速通过桥梁,行人重量取100 kg,Sxx(ω)由式(3)求得.

为验证方法的正确性,与Caprani[8]描述的方法进行对比.图2为MPIM-PEM方法计算的25 km/h下的时变方差值,与图3中DQ-PEM方法算得的25 km/h下的时变方差值曲线基本相符,方差峰值均为1.19×10-16.

图2 速度为25 km/h下人行桥跨中的时变方差 Fig.2 Time-varying variance in midspan of footbridge at 25 km/h

图3 不同速度下人行桥跨中的时变方差Fig.3 Time-varying variance in midspan of footbridge at different velocities

3.1 速度对随机振动的影响

图4所示为不同速度下简支梁式结构跨中的位移演变功率谱.为方便对比数值结果,采用荷载瞬时位置(x=v·t)表示x轴坐标.由图4可知,有两个峰值分别出现在4～6 Hz以及10 Hz附近,响应的第二个峰值出现在频率较高的位置,且峰值数值较第一个峰值大,对梁的振动起主要作用.通过对结构的自振分析得简支人行桥的一阶自振频率为4.7 Hz,响应演变功率谱峰值出现在自振频率附近,与荷载移动速度无关.当荷载移动速度为25 km/h时,第一个峰值在4.7 Hz左右为0.44×10-18,第二个峰值在10 Hz左右为1.995×10-18.荷载移动速度为50 km/h时,第一个峰值在5 Hz左右为0.4×10-18,第二个峰值在10 Hz左右为2.051×10-18.荷载移动速度为100 km/h时,第一个峰值在5.2 Hz为0.8×10-18,第二个峰值在10.5 Hz为2.296×10-18.荷载移动速度为100、50、25 km/h对应的跨中位移响应时变方差最大值分别为1.23×10-16、1.2×10-16和1.19×10-16,其中25 km/h以及50 km/h对应的位移时变方差最大值为100km/h的0.97倍和0.98倍.由图4可知,梁式结构跨中处的时变方差最大值随着荷载速度的增大而增大,最大值出现时间随着荷载速度的增大而后移.

图4 不同速度下人行桥跨中位移响应演变功率谱Fig.4 Evolution power spectrum of displacement response in span of footbridge at different velocities

3.2 约束条件对随机振动的影响

图5为在简支、η为1、5、10及固支约束条件下,其跨中在荷载以25km/h速度下的位移响应时变方差图,其峰值分别为0.13×10-15、0.19×10-15、0.93×10-15、2.38×10-15、8.1×10-15,在简支、η为1、5、10约束下的位移响应时变方差分为固支的0.016、0.023、0.115、0.294倍.

图5 不同约束条件下人行桥跨中的时变方差Fig.5 Time-varying variance in midspan of footbridge with different boundarie

图6为梁式结构在简支、η=5及固支约束下,其跨中在荷载以25 km/h速度作用下的位移响应演变功率谱.通过对结构的自振分析得梁式结构在简支、固支及η=5时一阶自振频率分别为4.773、10.820、7.346 Hz.从图5可知,梁式结构跨中的位移响应演变功率谱峰值均出现在其自振频率附近,简支约束条件下有两个峰值,第一个峰值出现在5 Hz为0.6×10-18,第二个峰值在9.6 Hz为1.64×10-18;η=5时也有两个峰值,第一个峰值在7.3 Hz为3.04×10-18,第二个峰值在11 Hz为2.24×10-18;而固支约束条件下只有一个峰值在10.5 Hz为6.19×10-16.

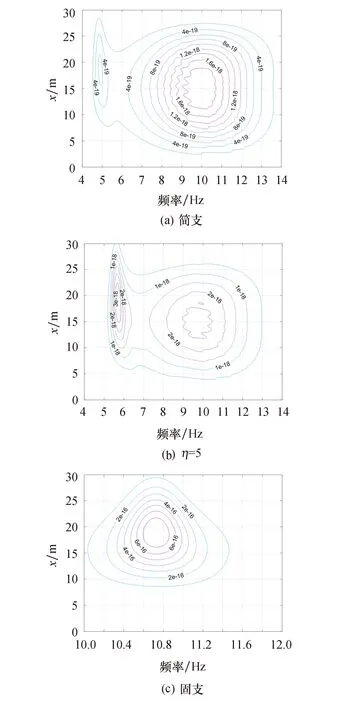
图6 不同约束下人行桥跨中的位移响应演变功率谱

4 结论

1) 计算结果验证了该方法的准确性和有效性,可以运用该方法求得在行人荷载激励下半刚性人行桥的非平稳随机响应.

2) 行人荷载激励下半刚性人行桥的跨中位移响应演变功率谱有多个峰值,峰值出现在自振频率附近,与荷载移动速度无关.

3) 算例结果表明当移动荷载为行人荷载时,响应演变功率谱的峰值出现在结构自振频率附近,梁式结构自振频率越大,其响应的演变功率谱和时变方差的峰值越大,可通过调整半刚性系数,控制半刚性人行桥的响应.