基于改进Crazy Climber算法的小波脊线提取

赵丽洁, 李雯雯, 刘 瑾, 晋东丽

(1. 天津农学院 水利工程学院, 天津 300072; 2. 河北工程大学 土木工程学院, 河北 邯郸 056038; 3. 天津大学 建筑工程学院, 天津300072)

近年来土木工程领域高速发展,工程结构越来越复杂,为保证结构安全性,进行结构健康监测十分必要.在结构健康领域,结构参数是反应结构性能的重要表述,而模态参数是结构参数中非常重要的参数之一,模态参数识别在土木工程领域一直是众多学者的研究热点.基于小波理论的参数识别应用广泛[1-5],其关键在于准确且快速的提取小波脊线.脊线提取方法分为单分量和多分量信号脊线提取两大类.由于小波脊线上包含相位与模值信息,所以发展出模极大值提取方法、相位法以及将二者结合的方法等.对于多分量信号脊线提取方法,较为简单的时频脊提取算法是峰值检测法[6].刘景良等[7]提出最大坡度法来实现瞬时频率的跟踪识别.王建华等[8]提出价值函数与动态规划思想结合,提取脊线精度优于模极大值法.张杰等[9]等基于加速度响应信号进行数据分解,提出结合自适应滤波提取同步压缩时频脊的方法来实现系统参数识别.此外,疯爬算法(Crazy Climber)也是一种比较广泛的小波脊线提取方法.Carmona等[10]首次提出Crazy Climber算法并用于多分量信号的脊线提取,较局部模极大值算法提取脊线精度更高.传统Crazy Climber算法引入模拟退火的思想,系统设定初始温度参数,随着温度逐渐降低,设定的Climber运动趋势越稳定,最后移动的点逐渐稳定聚集在脊线所在位置.温度下降越快,系统收敛越快,迭代次数越少,并很快得到广泛工程应用[11-12].

随着对Crazy Climber算法的深入研究,Xu等[13]发现采用退火冷却的温度函数容易导致算法无限增加迭代次数,温度下降速度过慢、运算时间过长,且受噪声影响,提取出来的脊线不平滑,工程应用受限.近几年,国内学者对Crazy Climber算法进行多方面的改进并实践应用.孙浩[14]限制提取到的脊线长度来剔除噪声引起的短小的“假”脊线,通过多方面的改进使识别小波脊结果更加准确.林炎等[15]采用淬火冷却替代退火冷却提高运算速度,提出一种新的温度函数.除此之外,在热处理工艺中,正火冷却同样可以快速降低系统温度.正火冷却算法以改变系统温度降低方式,温度可较快的降低到设定温度,从而影响随机点的迭代次数,促使每一个随机点高速聚集在脊线上,消减运算时间.正火冷却算法设定系统温度函数为T(t)=(T(0))/t,新的温度函数在迭代的最开始阶段保持着很高的复活概率,随着时间的延长,系统温度剧烈下降,很快收敛,节约运算时间.

综上所述,本文从小波脊线相关理论以及连续小波变换定义入手,针对传统Crazy Climber算法模拟退火算法计算时间过长的缺点,对Crazy Climber算法进行改进,提出采用模拟正火冷却算法跟踪提取时频平面中的小波脊点.通过一个自由衰减信号数值算例和一个二自由度粘性结构系统模拟对本文中改进Crazy Climber算法进行验证.通过框架模型试验,验证改进算法的正确性.

1 连续小波变换与小波脊线

(1)

时,称ψ(t)为母小波.将ψ(t)进行频率范围的变换得到一个小波序列:

(2)

式中:a、b分别为尺度、平移参数.

基于母小波ψ(t)的连续小波变换信号x(t)可定义为[16]

(3)

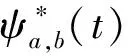
本文采用复Morlet小波作为母小波进行分析,其定义为

(4)

式中:fc为小波中心频率.

通过理论分析可知,针对每一时刻b,都有使小波变换WTx(a,b)的模取得最大值的对应尺度ar(b),即ar(b)是平移尺度b的函数,(ar(b),b)即为小波脊点,这些尺度的曲线拟合{ar(b),b}即称为小波脊线.而信号x(b)的瞬时频率φ′x(b)可由下式得到:

(5)

式中:ω0为小波基的中心频率.因此,瞬时频率能否识别准确与小波脊线的提取精度有着密切的关系,对模态参数识别小波脊线的提取至关重要.

2 改进Crazy Climber算法脊线提取

Crazy Climber算法的基本思想类似于模拟退火算法,对振动信号作连续小波变换后得到时频矩阵,在时频平面上随机地分布一些点(climber),令其在一定的规则下,以搜索极大值点为目标进行攀爬.设定一个初始温度,温度按规律逐渐降低,使各个脊点逐渐汇聚到一起,形成脊线.具体步骤如下:

将振动响应信号经过连续小波变换后的信号时频矩阵作为提取脊线的原始矩阵C,其大小为A×B,将A设为水平方向,B设为垂直方向,记在(i,j)(i∈[1,2,…,A],j∈[1,2,…,B])位置处的值为C(i,j).其中,C(i,j)为小波变换系数,i为表示时间离散点,j为小波频率离散点.

2.1 初始化

初始化一个度量矩阵D,并将其设为零矩阵;设置系统初始温度T(0),T(0)设为原始矩阵中最大值与最小值的差值.

在矩阵C={1,2,…,A}×{1,2,…,B}上存在N个爬升起始点,即为climber,climber的数量为N个,均匀分布在平面C上.

2.2 爬升规则

Climber在初始时刻时(t=0)的初始位置Xn(0)=(i,j),n∈[1,2,…,N].使climber按照以下规则进行爬升移动,从第t时刻的Xn(t)=(i,j)位置移动到第t+1时刻的Xn(t+1)=(i′,j′)位置.

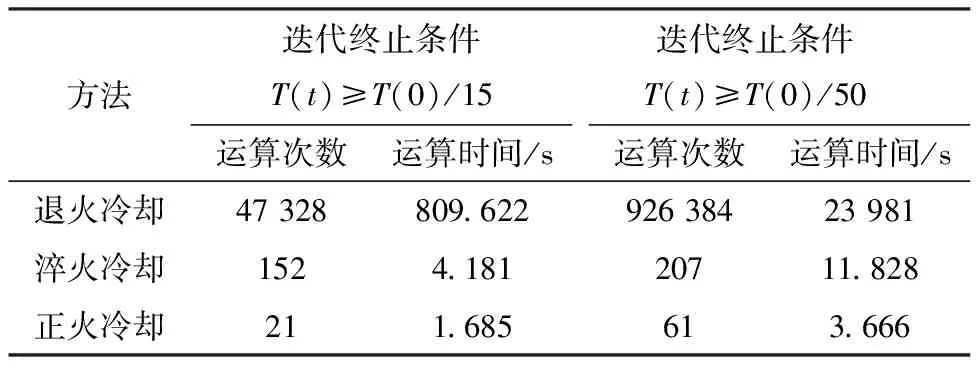
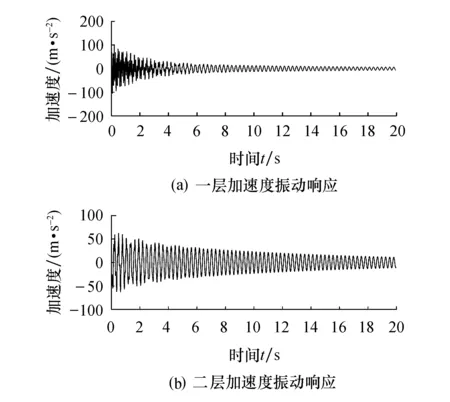
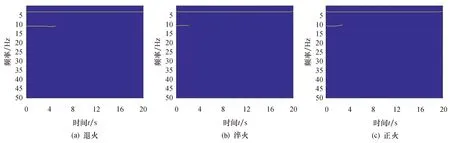
1) 水平方向上.分为两种情况,当climber不在边界上时,即0

2) 垂直方向上.在时间轴移动完成之后再在频率轴移动,该轴的移动规则分为是否移动两种情况.第一种情况,climber移动,与水平方向相同,climber按1/2的概率向上或者向下移动一格,即P{j′=j+1}=P{j′=j-1}=0.5.第二种情况,climber可以按一定规律选择移动或者不移动,其移动能力随时间的推移逐渐减弱,温度的降低使climber逐渐失去移动的活力.比较C(i′,j′)和C(i′,j)大小,决定是否移动.若C(i′,j′)>C(i′,j),climber垂直移动,即Xn(t+1)=(i′,j′);若C(i′,j′)≤C(i′,j),climber以概率Pt按照原计划移动,以(1-Pt)的概率不进行垂直方向上的移动,同时对系统当前温度T(t)进行更新.其中规定:

Pt=exp[C(i′,j′)-C(i′,j)]/[T(t)]

(6)

3) 重复1)、2)爬升过程,直到温度达到预期完成系统迭代,所有点都聚集在脊线上.图1为本文算法流程图.

图1 流程图

2.3 系统迭代结束条件

模拟退火冷却思想的温度变化设定为:T(t)=T(0)/log2t.在冷却方法中,包括正火、退火以及淬火冷却等,因冷却规则不同以至于冷却速率不同,退火冷却为T(t)=T(0)/log2t,淬火冷却为T(t)=T(0)/(1+σ)t,正火冷却为T(t)=T(0)/t.式中:T(t)为当前系统温度;T(0)为初始温度.

图2为三种冷却方式温度降低速率曲线,假定初始温度T(0)设置为1 400,时间间隔为10 s.

图2 三种冷却方法速率比较Fig.2 Comparison of three cooling method rates

由图2可知,使用正火冷却方法的温度降低速率明显快于另外两种冷却方法,可以快速达到预想温度减少系统迭代次数以完成脊线提取.虽然退火算法在前10 s温度降低极快,但是到达一定温度后,温度变化十分缓慢,达到理想温度耗时时间较长,不利于实际工程应用.因此本文采用正火冷却的思想代替退火冷却思想对系统温度进行降温,基于正火冷却思想的改进Crazy Climber算法来控制迭代次数.

3 数值模拟

3.1 指数衰减信号

为验证改进 Crazy Climber 算法对小波连续变换脊线提取的优越性,构造幅值为5,频率为50 Hz,衰减系数为10的指数衰减正弦仿真信号:

s=e-10t·5sin(100πt)

(7)

采样时间0≤t≤1 s,采样频率为1 024 Hz.选择cmor4-4为母小波进行连续小波变换.图3为指数衰减信号s(t)的时域波形与小波变换时频图,其中时频图反应了小波变换系数能量的分布情况,亮度较高区域表示能量较高.图4a为采用复Morlet小波与Crazy Climber算法所得脊点的连线,由图4a、b可知,信号s(t)的频率在50 Hz附近,与式(7)仿真信号中频率分量50相对应,验证了Crazy Climber算法的正确性.图4b为淬火冷却规则下所得脊点的连线,图4c为采用改进Crazy Climber算法提取到的脊线,可以看出三种冷却方法下的小波脊提取精度结果基本相同;再通过比较三者的迭代次数及运算时间来验证改进Crazy Climber算法的有效性,表1为三种不同算法提取脊线运算次数及所需时间.

表1 各冷却方法提取脊线运算次数及时间

图3 衰减信号时域图和时频图Fig.3 Attenuated signal time domain and frequency diagram

图4 冷却算法提取的脊线Fig.4 Ridge line extracted by annealing cooling algorithm

由图4c和表1可知,通过模拟正火冷却方式减少迭代次数、减少脊线提取所需时间,且没有降低脊线提取的精度,说明本文方法运算速度明显优于基于退火冷却思想的传统Crazy Climber算法.

大多数振动信号受噪声影响,为验证改进算法在噪声干扰情况下依然可以准确、快速地提取小波脊,本文在衰减信号s=e-10t·5sin(100πt)中加入SNR=6 dB的高斯白噪声进行数值模拟,限于文章篇幅只讨论该信噪比水平的影响.以复Morlet小波为母小波作连续小波变换所得的时频矩阵,存在噪声的时频曲线的分布.图5为传统Crazy Climber算法、改进Crazy Climber算法、淬火冷却下提取得到脊线结果,表2为三种算法运算次数和时间的比较.

表2 加噪后各冷却方法提取脊线运算次数及时间

图5 加噪后冷却算法提取的脊线Fig.5 Ridge line extracted by cooling algorithm after add noise

基于正火冷却的改进Crazy Climber算法提取的脊线结果以及系统运算次数、运算时间比较,可以看出与基于退火冷却的传统Crazy Climber算法相差不大的情况下,正火冷却的改进Crazy Climber算法所消耗时间相比于传统算法明显的缩减了上千倍甚至上万倍,验证了改进算法在加噪声后在提取脊线效率仍然存在很大优势.

3.2 两自由度系统仿真

为验证本文采用的脊线提取算法运算速度,将两自由度粘性系统进行仿真验证.图6为两自由度系统,m1=1 kg,m2=2 kg,k1=k3=2 256 N/m,k2=2 000 N/m,c1=c3=1 N·s/m,c2=0.11 N·s/m,施加一脉冲激励作为输入,fs=100 Hz,采样时间t=20 s,系统前两阶频率分别为3.5、11.3 Hz.

图6 二自由度振动系统

以质量块m1为研究对象,图7为复Morlet小波变换时间频率图,图8为该结构系统的加速度振动响应信号,图9分别为传统Crazy Climber算法、淬火冷却及改进Crazy Climber算法提取的小波脊线,比较本文算法与原始算法运算所需时间,验证改进算法的有效性.表3为在三种不同冷却规则下提取脊线所需迭代次数.

表3 两自由度系统各冷却方法提取脊线运算次数及时间

图7 含噪声时频图

图8 系统加速度振动响应

图9 退火冷却算法提取的脊线Fig.9 Ridge line extracted by annealing cooling algorithm

由表3可知,对于多自由度体系振动响应的脊线识别,在含有噪声时,基本不改变脊线精度的前提下,正火冷却算法效率所需时间明显优于淬火冷却和退火冷却,验证了本文算法较传统CrazyClimber算法效率提高.运用在实际工程中会需要更长时间,改进算法与原始算法精度上相差细微,效率却提高很大一步,更具实用价值.

4 试验验证

为验证改进CrazyClimber算法的有效性和准确性,设计3层剪切框架模型振动台验证性试验.在模型框架每层布置加速度传感器,通过振动台施加白噪声激励,采样频率设为512Hz,完整的试验装置图如图10所示.在振动过程中,通过在某一时刻割断框架附加柱来模拟框架模型的损伤破坏.

图10 框架模型试验装置

试验考虑振动过程中割断第二层附加钢柱的工况进行验证.图11为采集的顶层原始加速度数据以及频谱图.以复Morlet小波变换为母函数,对采集顶层的加速度数据进行连续小波变换,图12为未去噪的小波时频图.由频谱图和小波时频图可知,在附加柱割断前的前两阶频率分别为2.03、4.98Hz,在100s左右突然割断二层附加钢柱,频率变化为1.98、4.7Hz,并且框架模型刚度变小之后的第三阶频率6.98Hz也被激出.根据改进CrazyClimber算法提取小波瞬时频率脊线,如图13所示.表明改进CrazyClimber算法提取瞬时频率的准确性相对较高,验证了该方法的准确性.

图11 原始加速度数据及其频谱图

图12 时频图Fig.12 Time-frequency diagram

图13 改进Crazy Climber算法提取脊线Fig.13 Improved ridge line extracted by Crazy Climber algorithm

5 结语

1) 传统Crazy Climber算法可以较准确提取多分量信号的小波脊线,但较费时,不利于实际应用.本文在Crazy Climber算法基础上,改变温度冷却方式使脊点更快聚集在脊线上,提出基于正火冷却的改进CrazyClimber算法.通过单自由度及多自由度的数值模拟验证本文所提算法,仿真结果表明本文算法比原始算法运算次数大大减少,在不用影响频率脊线提取精度的前提下,大大节约提取过程所需时间,更有利于复杂数据的脊线提取应用.

2) 采用小波系数幅值最大值与最小值的差值作为系统初始化温度,温度T的初始值设置仍然是影响模拟正火冷却全局搜索性能的重要因素之一,目前还没有找到一个最优温度初值的选择原则,后续将继续深入探讨.