框架锚杆支护结构动力模型建立及响应分析

叶帅华, 冯文刚, 李京榜* ,2, 陶 晖

(1. 兰州理工大学 甘肃省土木工程防灾减灾重点实验室, 甘肃 兰州 730050; 2. 兰州工业学院 土木工程学院, 甘肃 兰州 730050; 3. 甘肃建筑职业技术学院 建筑工程系, 甘肃 兰州 730050)

随着我国一带一路推进,西北地区交通建设和城市建设处于高速发展的阶段,因受西北地区地形地貌所限,边坡工程数量不断增加.同时,西北地区又是强震活动的主要地区之一[1].地震作为边坡破坏的主要因素之一,控制地震作用下边坡的变形可保障人民生命财产安全.框架锚杆由于可改善边坡稳定性、有效限制边坡侧移等优点,目前在我国西北黄土地区深基坑开挖支护、边坡和桥台加固等工程实践中广泛应用.

地震作用下框架锚杆支护结构动力响应可反映边坡位移与支护结构的受力情况.目前,对支护结构动力响应的研究主要分为理论分析、振动台试验与数值模拟等.学者们对于支护结构动力响应的理论研究主要运用拟静力法+集中质量法,并获得了一定的成果.叶帅华等[2]通过建立支护结构动力计算模型,在立柱计算范围内以锚杆锚定点为中心,上下各取锚杆竖向间距的一半将框架和滑动区土体进行质量于地震惯性力对锚定点进行集中,通过求解地震作用下框架与土体系统的阻尼微分方程,分析了地震作用下锚杆的动力响应.董建华等[3-5]将计算单元范围内支护结构的地震惯性作用影响与动土压力以等效集中质量的方式附加在锚杆锚定点处,通过建立支护结构运动方程,分析了地震作用下支护结构内力与边坡位移响应,同时对锚杆自由段与锚固段微元体受力平衡进行了分析,并针对锚杆自由段与锚固段分别建立各自运动方程,分析了锚杆轴力随锚杆长度方向分布情况与时程响应.朱彦鹏等[6-7]以锚定点为中心,上下各取横梁竖向间距1/2的支护结构与滑移区土体将其质量于地震惯性力对锚定点进行集中,将支护结构划分为多质点体系,进而分析了支护结构的响应.此外,不少学者运用振动台试验法分析了边坡的动力响应.叶帅华等[8]通过相似比为1:10的框架锚杆支护黄土边坡的大型振动台模型试验,分析了地震作用下边坡动力响应规律与支护结构抗震性能.叶海林等[9-11]针对岩质边坡采用大型振动台试验,分析了地震作用下边坡破坏特征与地震作用下预应力锚杆、锚索的动力响应.王兰民等[12]开展了地震和降雨耦合作用下黄土边坡振动台模型试验,研究了地震和降雨耦合作用下黄土边坡的动力响应特征.姚爱军等[13]利用大型振动台进行悬臂抗滑桩加固边坡模型的振动试验,研究了悬臂抗滑桩加固边坡的地震响应.有些学者还通过依托实际工程,并运用数值软件对边坡的动力响应进行了分析[14-17].另外,国外学者对地震作用下锚杆的动力响应主要通过自由段与锚固段的力学行为机制进行研究[18-20].

综上所述,运用拟静力法+集中质量法对支护结构动力响应进行理论研究较为普遍.大多数学者运用质量集中法的具体做法是以锚定点为中心,上下各取锚固竖向间距1/2范围内的支护结构与滑移区土体对锚定点进行质量集中,从而将支护结构简化为多质点体系进行分析.简化的质量集中法虽可获得边坡锚定点处的动力响应,但不能直接获得边坡任意截面在地震作用下的位移响应与内力响应,故而动力响应较真实情况存在较大误差.为避免上述问题,本文以框架锚杆支护结构某中跨立柱单元为对象建立支护结构动力响应简化模型,运用力法与图乘法对支护结构动力响应进行求解分析,建立支护结构动弯矩和动位移与坡高之间的关系.运用模型算法与有限元法对实际工程算例进行对比,从而验证本文模型的合理性,计算结果的可靠性.

1 支护结构动力响应简化模型的建立

1.1 基本假设

1) 锚杆锚固体周围土体为各向同性的均匀弹性体.

2) 立柱抗弯刚度均为EI.

3) 忽略横梁、立柱的扭转效应.

4) 坡后土体为均质土层.

5) 忽略锚杆塑性变形与预应力损失.

1.2 支护结构动土压力分析

叶帅华[21]认为支护结构上动土压力随坡高的分布呈倒三角分布模式.本文认为:支护结构上动土压力随坡高的分布为三次曲线分布模式,分析如下:

根据立柱、横梁上作用的荷载可将支护结构划分为立柱单元和横梁单元[22],如图1所示.由于立柱为主要受力构件,故将立柱单元单独进行计算.

图1 单元划分Fig.1 Element division

图1中,sx为锚杆水平间距,s0为第一排锚杆距坡底的竖向距离,sy为上下排锚杆竖向间距,sv为最上排锚杆距坡顶的竖向距离.η1为立柱计算系数,η2为横梁计算系数,一般取0.75[22].

对于土质均匀的边坡,地震时滑动区土体由坡顶至坡脚近似呈倒三角分布.则框架预应力锚杆加固边坡剖面如图2所示.

图2 框架预应力锚杆加固边坡剖面图 Fig.2 Sectional diagram of slope supported by frame prestressed anchors

基于图1、图2,立柱单元上动土压力计算公式为[21]

式中:i=1, 2, …,n;pai为立柱单元上yi高度处动土压力强度;msi为yi高度处立柱单元内土层的质量;khi为yi高度处水平地震作用系数;yi为边坡任意位置距坡底的竖向高度;γ为土体重度;νur为土的泊松比;T为土的振动周期,T=2πcosωt/ω;α为边坡坡角;β为直线滑移面与水平面的夹角;Es为土的压缩模量;ρs为土的密度;υP为土的压缩波速;ω为地震波频率;f(ξ)为无穷函数z=(ξ)的导数,如下式所示:

(4)

式中:K为常数,根据初始条件α=bπ和β=aπ确定.

图3 水平地震加速度响应Fig.3 Horizontal seismic acceleration response

由图3可知,当坡高H≤40 m时,任意高度yi处水平地震作用系数khi为

(5)

当坡高H>40 m时,任意高度yi处水平地震作用系数khi为

(6)

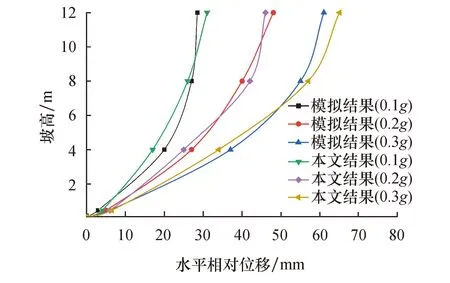
0.6H

(7)

式中:kh为坡底水平地震作用系数.

依据上述的式(2)与式(5～7)可知,msi、khi均为关于yi的一次函数,再结合式(1)可知,pai为关于yi的三次函数,故支护结构上动土压力随坡高的分布为三次曲线分布模式.

1.3 模型的建立

取图1中某中跨立柱单元为研究对象,依据基本假设,将立柱简化为抗弯刚度均匀的竖向杆件,依据锚杆工作机理将自由段简化为线弹簧,在考虑土体阻尼的影响下将锚固段简化为线弹簧与牛顿粘壶,又因基础桩限制了坡脚处支护结构的转动,故将坡脚处简化为固端约束.基于前节分析可知,支护结构上动土压力随坡高的分布呈三次曲线分布模式.由于支护结构的锚固作用使得支护结构在地震过程中与坡后土体不发生相对位移,并且可将支护结构看作弹性体,因此,认为支护结构与边坡具有相同的加速度放大效应,故支护结构惯性力分布取图3所示的线性分布模式.

2 动力响应分析

2.1 支护结构动弯矩M求解

支护结构动力响应简化模型如图4所示,将锚杆自由段看作线弹簧,则其轴力为线弹簧上的轴力;锚固段作用看作线弹簧与牛顿粘壶耦合,则其轴力为线弹簧上的轴力与牛顿粘壶上的粘滞力之和.依据文献[25]可知,第i排锚杆的轴力Ni(x,t)为

图4 支护结构动力响应简化模型Fig.4 Simplified dynamic response model of supporting structure

(8)

式中:Ei1Ai1、Ei2Ai2分别为第i排锚杆自由段与锚固段的抗压刚度;ui1(x,t)、ui2(x,t)分别为第i排锚杆自由段与锚固段的位移函数;lf为锚杆自由段长度.

锚杆轴力沿杆轴方向分布不均[25],而作用在立柱上的锚杆轴力为锚定点处的锚杆轴力,即:

Xi=Ni(0,t)

(9)

如图4所示,在已知锚杆轴力基础上可将每根锚杆看作一个约束,再将锚杆取作多余约束,则力法的基本体系如图5所示.

图5 力法基本体系Fig.5 The basic system of force method

由图5可知,由轴力Xi引起基本体系弯矩Mi与外荷载(支护结构上动土压力与支护结构惯性力)引起基本体系弯矩Mp如图6所示.

图6 Xi与外荷载作用下基本体系弯矩图Fig.6 Bending moment diagram of the basic system under Xi and external loads

如图6所示,立柱动弯矩可表示为

M=Mi1+Mi2+…Mii+Mip

(10)

式中:Mi1、Mi2、Mii为基本体系在X1、X2、Xi单独作用下立柱的弯矩;Mip为基本体系在外荷载(支护结构上动土压力与支护结构惯性力)作用下立柱的弯矩.

将式(10)展开为一般式,可表示为

(11)

式中:yi为所求截面高度;i为所求截面高度yi以上锚杆排数;支护结构可视为由一系列水平无限薄层组成,则坡顶处支护结构惯性力FmH与任意高度处支护结构惯性力Fmi可表示为

(12)

式中:ρ为支护结构密度;d为支护结构厚度;kH为坡顶与坡底的水平地震作用系数差值;Δkhi为所求截面与坡底的水平地震作用系数差值;ΔkH为坡顶与坡底的水平地震作用系数差值.

2.2 支护结构动位移Δ求解

通过图乘法对支护结构位移进行计算,在所求截面高度处作用单位荷载F=1时支护结构基本体系弯矩图如图7所示.

图7 单位荷载作用下基本体系弯矩图Fig.7 Bending moment diagram of the basic system under unit load

由图7可知,单位荷载作用下支护结构基本体系任意截面弯矩为

(13)

式中:hi为单位荷载作用点距坡底的竖向距离.

基于上述分析,支护结构任意高度处位移可表示为

(14)

将式(11)与式(13)带入上式,可将式(14)转化为

(15)

3 算例分析

3.1 工程概况

甘肃省天水市某小区边坡支护,坡高为12 m,边坡与水平面夹角为80°,本工程抗震设防烈度为8°,边坡土体参数见表1.采用框架锚杆挡墙支护, 框架梁、柱截面尺寸为0.3 m×0.3 m,挡土板厚度为0.1 m,采用C30级混凝土,锚杆设计结果见表2.

表1 土层参数

表2 锚杆参数

3.2 数值模拟

为验证本文建立模型的合理性、计算结果的可靠性,采用Geo-Studio有限元软件中Quake模块对算例进行数值模拟,模型尺寸为20 m×37 m,其中,土层参数如表1所列,黄土厚度为14 m,中砂厚度为3 m,第四系全新统(Q4)卵石厚度为2 m,第四系下更新统(Q1)卵石厚度为1 m.土的压缩模量Es为1.05×104kPa、剪切波速vs为280 m/s、阻尼比ξ为0.005;立柱弹性模量为2.5×107kPa,截面积为0.16 m2;锚杆自由段弹性模量为2×108kPa,截面积为0.001 m2;锚固段弹性模量为8×106kPa,截面积为0.018m2,锚杆长度参数如表2所列,有限元模型如图8所示.为进行多元化对比分析,在输入地震动力时分别输入峰值加速度为0.1g、0.2g、0.3g的EI-Centrol水平波,持时均为30 s,其中,峰值加速度为0.3g的EI-Centrol水平波如图9所示.

图8 有限元模型Fig.8 Finite element model

图9 EI-Centrol水平波激励(0.3g)Fig.9 EI-Centrol horizontal wave excitation (0.3g)

3.3 结果对比分析

将数值模拟与相关文献以及本文方法获得的支护结构上动土压力峰值、锚杆轴力峰值、支护结构水平相对位移峰值、立柱动弯矩峰值进行对比分析.

3.3.1支护结构上动土压力峰值对比分析

基于工程实例,由本文方法、文献[21]中方法与有限元法得出的支护结构上动土压力峰值对比如图10所示.

图10 支护结构上动土压力峰值对比Fig.10 Comparison of maximum dynamic earth pressure on supporting structure

由图10可知,由文献[21]中方法得出的支护结构上动土压力峰值较本文方法与有限元法的结果相差较大.分析认为,文献[21]中的动土压力计算方法忽略了滑移区土体质量与坡高的关系,未考虑边坡加速度放大效应,因此得出的动土压力峰值大致呈倒三角分布,这种方法得出的动土压力峰值较真实情况具有一定偏差.而本文方法与有限元法得出的支护结构上动土压力峰值吻合度较好,且动土压力峰值随坡高的分布均呈现三次曲线分布模式,随着地震波峰值加速度的增加,支护结构上动土压力峰值变化规律越明显,此外,由图可知两者计算结果吻合度较好.

3.3.2锚杆轴力峰值对比分析

由数值模拟结果与文献[25]中方法得出的锚杆轴力峰值对比如图11所示.

图11 锚杆轴力峰值对比Fig.11 Comparison of maximum axial force of anchors

由图11可知,在不同加速度峰值的地震波作用下,锚杆轴力峰值随坡高的变化均呈现出先增大再减小的分布规律,其最大值均出现在第三排锚杆处,因此在进行边坡支挡结构设计时要采用“强腰”的设计理念.此外,在不同加速度峰值的地震波激励作用下,锚杆轴力峰值随坡高的分布规律大致相似,不同加速度峰值的地震波激励对锚杆轴力峰值分布规律的影响较小.

3.3.3支护结构水平相对位移峰值对比分析

由数值模拟结果与本文方法得出的支护结构水平相对位移峰值对比如图12所示.

图12 支护结构水平相对位移峰值对比 Fig.12 Comparison of maximum horizontal relative displacement on supporting structure

由图12可知,支护结构水平相对位移峰值随坡高呈现出持续增长的趋势,并且两种计算结果吻合度较好.分析认为,支护结构上动土压力峰值随坡高呈现三次曲线分布模式,锚杆自由段又可简化为线弹簧,因此可知支护结构水平相对位移峰值随坡高不断增加.在此基础上由胡克定律可知,随坡高的增加锚杆发挥的作用也随之增加,从而导致支护结构水平相对位移峰值增长速率随坡高的增加表现出衰减趋势.

3.3.4立柱动弯矩峰值对比分析

由数值模拟结果与本文方法得出的立柱动弯矩峰值对比如图13所示.由图13可知,立柱在除顶跨以外每一跨都存在两个反弯点,每跨最大正弯矩峰值出现在跨内(坡面外侧受拉为正).随坡高的增加,跨内最大正弯矩峰值不断增加,在坡高10 m处立柱正弯矩峰值达到最大,立柱每跨最大负弯矩峰值均出现在锚定点处,且随坡高的增加,最大负弯矩峰值也随之增加,在坡高12 m处立柱负弯矩峰值达到最大.分析认为,动土压力是支护结构所承受的主要荷载,而锚杆的作用又相当于支座,故可将立柱看作多跨连续梁,基于上文分析可知,随坡高的增加立柱上所受的动土压力峰值呈三次曲线分布,因此,随坡高增加立柱每跨跨内最大正弯矩峰值与锚定点处最大负弯矩峰值不断增加,此外,由于工程算例中最上排横梁上边缘距离坡顶0.25 m,与坡高12 m相比可忽略不计,因此可将最上排锚杆处弯矩峰值看作坡顶弯矩峰值.

图13 立柱动弯矩峰值对比Fig.13 Comparison of upright column maximum bending moment

4 结论

1) 建立的支护结构动力简化模型能较准确的反映支护结构形式及受力情况.

2) 地震作用下支护结构上动土压力峰值随坡高的分布为三次曲线分布模式,其分布规律随地震波峰值加速度的增加而越发明显.

3) 支护结构水平相对位移峰值随坡高变化呈现出正相关趋势,但增长速率随坡高的增加均呈现出衰减趋势.

4) 锚杆轴力峰值分布随坡高增加呈现出先增大再减小的分布规律,其最大值均出现在第三排锚杆处,且不同加速度峰值的地震波激励对锚杆轴力峰值分布规律的影响较小,该研究结果为进行边坡支挡结构设计时采用“强腰”的设计理念提供了依据.

5) 立柱动弯矩峰值在除顶跨以外每一跨都存在两个反弯点,每跨正弯矩峰值的最大值出现在跨内,且随坡高的增加呈现出增长趋势;负弯矩峰值的最大值均出现在锚定点处,且随坡高的增加也呈现出增长趋势.