考虑出行特征的电动汽车协同充电调度优化研究

葛显龙，王博，杨育树，杨昙月，尹作发

(重庆交通大学，a.经济与管理学院；b.交通运输学院，重庆 400074)

0 引言

近年来，我国电动汽车渗透率和保有量双双呈现高速增长趋势，大量公共充电设施如雨后春笋般开始建设，桩车比由2015 年的1∶11提高至1∶2.4[1]。然而，由于电动汽车充电需求的大规模随机性、充电网络结构不合理及供电网荷载波动等原因，导致公共充电设施无法得到有效利用，并未解决电动汽车充电供需不均衡的问题，“有车无桩”“有桩无车”的现象频繁发生，用户出行体验差，充电设施资源利用效率低下。为解决充电难的现实问题，国务院办公厅提出进一步构建高质量充电基础设施体系指导意见，鼓励推广应用智能充电基础设施，利用车联网强化对电动汽车充放电行为的调控能力。同时，政府开始在热点区域公用充电设施实行预约充电，以便掌握用户需求特征，引导用户错位错峰充电[2]。然而，错峰错位充电不仅需要从用户角度引导电动汽车选择充电站，还需要从站点的角度实时调整充电功率，实现智能有序充电。

由于充电需求与供给在时空维度下的不匹配，导致充电资源利用率低和电网负荷波动大等问题凸显，严重影响电动汽车用户出行体验及站点的高效运营。为此，国内外学者针对电动汽车协同充电调度问题展开研究。ZHOU等[3]提出一种考虑充电紧急度的电动汽车协同充电调度方法，建立以最小化总峰谷负荷差为目标的协同充电调度优化模型，将负荷需求从高峰时段转移到低谷时段。KHONJI等[4]为缓解充电需求高峰，提高清洁能源的利用率，研究了存在最小功率需求的电动汽车充电调度优化问题。YIN等[5]构造一个动态多目标优化方案，在每个时间段内，通过调整充电开始时间或可变充电功率，缓解电网负载波动。HAUSLER等[6]研究充电网络中充电需求的平衡问题，提出一种完全分散的随机平衡算法。KUMAR等[7]将电动汽车协同充电进一步分为时间协同充电和功率协同充电，研究不同优先级标准对电动汽车充电性能和充电公平性的影响。SPENCER等[8]证明合理的调度可以有效地将负荷从高电网成本和拥挤的时段转移到凌晨和中午电网成本较低的时段。WANG等[9]分别考虑电动汽车数量对充电站运行的影响及单个用户的出行成本，并确保在时变路网中到达选定的充电站。上述研究从充电站的角度，通过调整电动汽车充电时间和功率缓解电网的负载波动，没有考虑用户的实际出行需求对充电调度带来的影响。

随着智能交通的发展，一些学者开始对预约充电模式在调度中的应用展开了研究，HOU等[10]研究一种电动汽车预约充电调度问题，根据用户的时间偏好和车辆的充电状态，最大化所有用户的社会福利。KUMAR等[11]通过考虑充电站预约的延迟和收费时间，根据充电站的可用性和类型调度电动汽车充电，并优化充电站的管理。PAUDEL等[12]考虑用户充电紧迫性，引入充电优先级。在可用充电功率和充电站容量的约束下，最大限度地提高用户的满意度。ERDOGAN等[13]建立一个多目标充电调度优化模型，分别设计时间间断和连续的智能充电策略，发现采用弹性策略可获得单位成本最低和电网资产利用率最高的调度方案。上述研究假定所有用户一定接受充电调度方案，分别从电动汽车用户、站点及电网等多方视角出发研究电动汽车预约充电调度问题，忽略了电动汽车用户服从调度的意愿问题。

因此，一些学者们对电动汽车用户充电行为及充电调度激励机制展开研究，BRUCKMANN等[14]通过数据调查，分析用户对等待时间、充电时间、价格、能源来源和便利设施等因素的偏好影响。LIAO等[15]通过分析大量充电需求，将出行需求和充电行为分为“提前计划”“事件触发”两类。毕军等[16]采用数据挖掘分析方法，分析和建立电动汽车的充电行为模型。杨烨等[17]按照充电行为类型提取车辆行程，发现电动汽车续航里程、出行距离及出行时间等因素显著影响电动汽车的充电行为。何方等[18]针对驾驶员绕路充电现象，考虑驾驶员在不同充电速度和排队情况下的充电站选择行为，研究电动汽车最短路径问题。此外，在分析电动汽车用户充电行为的基础上，学者们开始研究电动汽车充电调度激励机制，CHEN等[19]提出一种考虑用户充电选择的多目标调度方法，确定电动汽车的最优充电，并分析电动汽车用户充电偏好是如何影响电动汽车的充电成本和电网的负荷变化。WANG等[20]设计一种基于几何的充电引导算法，考虑行驶距离和充电路线与目的地方向的一致性，从整个行驶链的角度为电动汽车驾驶员选择更好的充电站。葛显龙等[21]从路网视角研究电动汽车充电社会成本最小化问题，提出一种充电激励方案，引导车辆合理选择充电站，结果表明，经济激励可以有效缓解出行和充电拥堵问题。XIONG等[22]将行为建模和优化集成到出行激励设计中，开发一个集成的个性化旅行者信息和激励方案，通过行为研究和实证建模量化个性化的货币激励。上述研究通过刻画电动汽车用户的充电选择行为，并多采用经济激励引导和改变电动汽车用户的充电选择，但对具体经济激励的计量方式研究尚不成熟。此外，程杉等[23]以充电站收益最大化为目标，结合充电需求和电网功率约束构建电动汽车充电调度模型，并针对分时电价策略进行仿真分析，结果表明，分时电价可以将部分电网高峰期充电需求向低谷期转移，但会造成新的波峰，对于平抑负荷波动的效果较差。

综上，许多学者采用分时电价和预约充电等手段缓解电动汽车充电需求与供给之间的时空矛盾，以平滑电力负荷波动和减少充电站排队。在此基础上，学者们开始考虑电动汽车用户特征对协同充电调度的影响，通过分析电动汽车用户的充电偏好、充电行为及出行类型等因素，更好地激励电动汽车用户服从协同充电调度方案。然而，不同用户的出行特点存在显著差异，用户是否服从充电调度，很大程度上受到其出行需求的影响。一些用户在出行途中可以选择不同的充电站进行充电，由于到达不同站点的时间不同，对这部分用户的调度可以实现充电需求在时间和空间上的调节。为此，本文结合电动汽车用户的出行特征，提出经济激励调度和站点充电功率分配策略，通过改变车辆充电站点和充电时间实现充电供需时空平衡，构建电动汽车协同充电调度优化模型，并设计改进遗传算法进行求解。最后，通过算例仿真验证模型和算法，为城市电动汽车智慧充电调度提供决策参考。

1 问题描述

城市路网中的电动汽车用户在续航不足时，需要前往充电站进行充电，根据电动汽车用户的出行特征可以分为3 种出行类型，分别是通勤出行、计划出行以及临时出行[15]。通勤出行用户和计划出行用户通过预约充电的方式准确获取充电资源，临时出行用户则随机到达充电站进行充电。通勤出行用户希望在工作场所附近的充电站进行充电，并在充电站长时间停留，因此，充电站只需保障电动汽车在离开时充满即可，在充电时间上拥有较大的选择空间。但通勤出行用户的时间敏感性较强，在充电站点的选择上几乎不会改变，他们必须按时到达充电站，保证个人后续事务顺利进行；计划出行类用户通常由于续航限制需要在途中进行充电，此类用户的充电时间在总出行时间中占比较小，可以在出行前提前规划充电路线，因此，用户对充电时间的敏感性相对较弱，在续航可达范围内，具有较大的充电站点选择空间；临时出行用户由于其续航不足而就近充电，他们希望尽快获取充电资源并对充电排队有一定的忍耐力，当续航达到一定水平后离去。不同出行类型的用户特征如表1所示。

表1 不同用户出行类型的特征Table 1 Characteristics of different user travel types

通过对电动汽车用户出行特征的分析，归纳为3 种不同的出行类型。针对不同类型的特点，采用经济激励和功率协调策略缓解电力需求波动。因此，本文研究的问题如图1 所示，通勤出行用户C从住所出发前往工作单位附近的充电站，停留至下班后离开，用户C 不能更换充电站，但充电时间的选择空间较大，可以转移到电网低谷期进行充电；计划出行类用户P在出行中经过多个充电站，可以选择车辆少和负载小的站点进行充电，充电需求在时间和空间维度进行调整；临时出行用户T不接受更换充电站，并期望尽快获得电力，难以在时空维度调整需求。

图1 考虑出行模式的电动汽车协调充电调度问题Fig.1 Schematic diagram of coordinated charging scheduling problem for electric vehicles considering travel modes

考虑在一个城市交通路网G(N,A) 中，N为节点集合，A为路段集合，路网中分布着多个充电站，用集合I表示。根据电动汽车用户特征，将用户分为通勤出行、计划出行及临时出行这3 类，分别用集合Kc、Kp、Kt表示。将T时间长度内分为t个时间段，充电站向电网购买电力的分时电价为pil，站点向电动汽车用户的售电价格为s。在满足电动汽车续航可达和充电需求Sk的基础上，充电站需要决定电动汽车充电调度方案xijk及站点内各时段功率输出yjkl，使得站点总收益最大化。

2 建立模型

2.1 符号说明

所有符号及其含义说明如表2所示。

表2 符号及含义说明Table 2 Explanation of symbols and meanings

2.2 问题假设

充电调度问题需要考虑城市交通路网中车辆充电场景的各种约束，为简化问题并不失模型的一般性，做出如下问题假设：

假设1 调度系统能够完全获取用户车辆情况、出行特征及充电站相关信息。

假设2 电动汽车的最大荷电量和充电功率一致，且充电量随时间线性增加。

假设3 计划出行类用户对时间敏感性较弱，仅关注出行的经济成本，且在接受调度补偿后，按照调度方案选择充电站进行充电。

假设4 充电站向电动汽车用户销售的电价不随时间变化。

假设5 计划出行类用户的车辆行驶速度不变。

假设1 确保调度模型的信息基础；假设2 简化模型的计算，在现实中可以按照各车型设置，且不影响模型性质，并且将电动汽车充电时间的计算线性化，保证模型复杂度的可控性；假设3 保证调度的可行性，原因是计划旅行类用户接受补偿后到达调度站点的综合经济成本最小；假设4简化模型的计算，虽然充电站向用户提供的分时电价会改变不同时段充电需求数量，但是，在充电需求已知的情况，已知固定的分时电价对协同充电调度优化模型没有影响；假设5 可以拓展出具有不同车速的场景，但这种拓展并不会提高模型的准确性，反而会使模型的计算量增加，因此，为简化计算，对车速进行一致性假设。

2.3 用户协同充电策略及度量方法

计划出行类用户在出行中会经过多个充电站，对其进行调度能够在时空维度调整充电需求。电动汽车用户的充电选择主要受金钱和时间两个因素影响[22]，由于电动汽车用户的充电偏好涉及隐私问题，难以准确获取。且在大规模充电调度时，用户的充电偏好差异将会使调度补偿分配不公平。同时，计划出行类用户可以在出行前提前规划充电路线，在车辆续航能够到达充电站点的前提下，对时间的敏感性较弱。因此，本文仅考虑使用经济补偿激励计划出行类用户服从调度。

电动汽车用户通常以出行成本最小化为目标，选择其出行路径和充电站点。由于协同充电调度改变了用户的充电站点，用户的出行路径变化可能会导致出行成本上升，为使电动汽车用户服从调度，需要给予一定的补偿。这种补偿是根据用户包含至少1 个充电站的最短出行路径与包含特定充电站的最短路径之间差值决定的。补偿的大小与电动汽车用户绕行距离成正比。假设1 个简单路网中具有4 个节点和5 个路段，路段上的数字表示两个节点之间的距离，其中，节点2和节点3均有充电站。如图2 所示，1 个电动汽车用户从节点1 出发，目的地为节点4，中途需要充电，该车辆包含充电站的最短旅行路线为1-2-4(原始路线)，路线长度为2+4=6。由于节点2 处的充电站存在排队，要调度电动汽车用户前往节点3进行充电，其旅行路线变更为1-2-3-4(绕行路线)，路线长度为2+2+3=7。调度电动汽车用户充电时的绕路距离为1，需要对其进行经济补偿，以诱导用户服从调度。

图2 充电调度经济补偿示意Fig.2 Schematic diagram of charging scheduling economic subsidies

假设计划出行类电动汽车用户k包含至少一个充电站的最小旅行成本为，调度其前往充电站i时，电动汽车的绕路成本为，其中，为电动汽车用户k经过充电站i的最小旅行成本。因此，调度电动汽车用户k前往充电站i进行充电的调度经济补偿，m为单位绕行距离的经济补偿。

2.4 建立考虑出行特征的电动汽车协同充电调度优化模型

电动汽车用户的无序充电活动导致充电站购电成本高和设施利用率低等问题。在考虑电动汽车不同出行特征的基础上，从充电站收益最大化的角度出发，通过经济激励改变电动汽车用户的充电选择，以缓解电动汽车充电供需的时空矛盾。站点通过向电动汽车售电产生盈利，并为激励电动汽车用户服从充电调度而付出调度成本。目标函数为

式中：第1项为充电站向电动车辆售电所获得的收入；第2项为调度计划出行类用户前往充电站的经济激励，即充电站的调度成本。

约束条件为

式(2)表示分配给同一个充电桩的电动汽车之间不能有时间冲突；式(3)表示通勤出行类用户和计划出行类用户必须且仅分配一个充电桩；式(4)表示临时充电类用户至多分配一个充电桩；式(5)和式(6)通过引入辅助变量wjkk′解决决策变量xijk相乘所导致的非线性问题；式(7)表示任意时间段，充电桩充电量为非负数，且小于车辆时间段内的最大充电量；式(8)表示任意时间段，充电站总输出功率约束；式(9)表示任意电动汽车用户在离开充电站前充电至所需电量；式(10)表示充电桩在没有电动汽车用户占用的情况下，充电量为零；式(11)表示变量ujkl与xijk之间的关系；式(12)表示电动汽车用户k到达不同充电站i的时间；式(13)表示电动汽车用户k到达和离开充电站的时间和占用充电桩之间的逻辑约束；式(14)表示计划出行类用户前往充电站的剩余里程约束；式(15)是模型中变量的取值范围。

2.5 模型分解

电动汽车协调充电调度问题是一种特殊的资源受限调度问题，属于NP-hard问题[24]，随着电动汽车车辆数的增加，求解时间将呈指数上升。因此，需要分解模型，将问题分解为含有xijk决策变量的主问题和含有yjkl的子问题，加快求解时间。首先，由于模型中具有两个决策变量，分别是xijk和yjkl，xijk为0-1变量，yjkl为整数变量，且xijk和yjkl之间存在逻辑关系(式(10)与式(11))。每次xijk取值的改变对yjkl取值有很大影响，通过对模型的分解，将问题转化为0-1型整数规划的主问题和整数规划的子问题，便于求解。

其次，模型引入ckk′表示电动汽车充电时间之间的冲突，并通过式(2)保证分配给同一个充电桩的电动汽车之间不存在时间冲突。然而，xijk的不同取值会导致计划出行类用户到达不同站点的时间不同，车辆在充电站停留和占用充电桩的时间随之改变，不同车辆之间的时间冲突判断将会变得十分复杂，即辅助变量c是一个随xijk取值变化而动态变化的0-1矩阵，直接求解模型时，随着电动汽车数量增加，模型中c的维度和有关约束数量急剧上升。通过对模型的分解，在给定xijk下，c为固定二维矩阵，提前计算多个固定c的值远比在精确算法中解决动态变化的c节省时间。

因此，可以将模型转化为以下两个问题：

主问题(Master Problem,MP)为

约束条件为：式(2)～式(6)和式(11)～式(14)。

子问题(SubProblem,SP)为

式中：f(y)为站点收益，其变化取决于各时段车辆的充电量yjkl。

约束条件为式(7)和式(8)，以及

式中：xijk为主问题传递到子问题的固定值。针对一组给定的电动汽车充电分配调度方案xijk，子问题是一个关于单个充电站内部充电桩功率分配的整数线性规划(ILP)问题，相比原模型，模型复杂性和求解难度有明显下降。

3 设计算法

通过分析模型，协调充电调度优化模型的决策变量为xijk和yjkl，其中，xijk为0-1变量，表示若用户k在充电站i的充电桩j充电。yjkl为非负整数变量，表示充电桩j对电动汽车用户k在时间段l中的充电量。模型的解空间巨大，传统优化方法很难求解。可以选择使用通用性强和收敛快的遗传算法进行求解。然而，若采用遗传算法直接求解，编码和算子操作将变得复杂，求解速度和精度难以保证。若直接采用求解器求解，由于决策变量数量和维度较多，属于NP-hard[24]，求解速度难以接受。因此，尝试使用遗传算法和求解器结合的方式求解问题，其中，遗传算法用于求解电动汽车的充电站/桩的调度分配问题，针对0-1 决策变量xijk，将车辆分配给不同充电站的充电桩上。当每个站点车辆和充电桩的匹配关系确定后，通过调用Gurobi/Cplex等成熟的商业求解器求解子问题，并将其嵌入遗传算法中，解决充电站充电功率分配问题，针对整数决策变量yjkl，确定充电站中各时段充电功率的分配方案。将问题进行分解后，决策变量的规模减少，求解速度加快，并且精确求解也能够保障一定的求解质量。

(1)编码与适应度函数设计

根据计划出行类用户可以选择不同充电站充电的特点，设计改进遗传算法的编码方式为实数编码，染色体长度为计划出行类用户的数量，第j个基因位的取值表示电动汽车用户k前往充电桩的编号，如图3所示。

图3 改进遗传算法编码规则Fig.3 Schematic diagram of improved genetic algorithm encoding rules

以充电站总收益最大化为优化目标，可以直接使用目标函数式(1)作为适应度函数。在给定染色体编码下，逐个遍历充电站，求解单个站点的具体功率分配方案，该部分可以进行二次编码计算，也可以通过yalmip调用Cplex、Gurobi等求解器求解。

(2)初始解的生成

传统遗传算法采用随机生成方式产生初始解，这种方法生成的初始解质量难以保证。为此，设计贪婪算法构建一个优质解作为初始解之一，加快求解。

(3)选择算子

由于目标函数是综合收益最大化，因此，采用轮盘赌方式进行选择，单个染色体的适应度f越大，被选中的概率越大。

(4)自适应交叉与变异算子

交叉算子有3 种：单点交叉、双点交叉及多点交叉，在交叉的过程中，随机选取一种交叉方式交换两条染色体上基因或者基因片段。变异算子选择染色体上的某个基因或某一段基因，将其进行转换，得到一个新的染色体。为使算法快速收敛的同时，避免陷入局部最优，将fmax作为群体收敛程度的指标，其中，fmax是种群适应度的最大值；是种群适应度的平均值。当种群的收敛程度一致时，算法可以收敛到全局最优解或局部最优解。此时，fmax的值会降低，因此，交叉概率Pc和突变概率Pm应该相应增加，以增加种群的多样性，从而使种群跳出局部最优区域。在群体中，每个个体对应的Pc和Pm是不同的，即

式中：k1,k2,k3,k4为小于1的定值。

(5)不可行解的修复

在生成初始解和遗传算子生成新解时，部分染色体方案中可能存在多个电动汽车分配到同一个充电桩的情况，导致充电桩的占用发生冲突。为此，在遗传算法中加入检查和修复环节，逐个检索染色体编码，当发现充电桩占用冲突时，搜索选择占用时间较短的车辆更换充电桩，这是一种类似贪心算法的处理方法，若解仍不可行，则采用罚函数法，保证种群向最优可行解的方向进化。

(6)优秀基因片段保留策略

为保证算法的快速收敛，采用优秀基因片段保留策略，每代种群中，适应度前10%的染色体将被记录，对比他们相同的基因段，作为优秀基因片段，该部分片段将作为整体参与交叉，并且不接受变异算子的改变。参考禁忌搜索算法禁忌表的思想，每代优秀基因片段保留后续5 次迭代不变，超过5 次迭代则移除优秀基因片段，保证种群多样性。

4 算例分析

为检验所提出模型和算法的有效性，本文分别在小规模经典路网和大规模现实路网上进行算例分析，并采用改进遗传算法求解。设定改进遗传算法最大迭代进化次数为200次，每代种群个体数为100 个，初始交叉概率为0.8，初始变异概率为0.3，算法使用MatlabR2021a 软件编程，并在CPU 为Intel(R)Core(TM)i7，内存为16 G 的笔记本上运行实现。

4.1 经典网络算例测试

(1)数据基础

以典型的Nguyen-Dupius路网为例验证模型的有效性，该路网由13个节点和19个路段组成，路网中分别在节点6、节点9 和节点11 设有充电站，如图4所示。

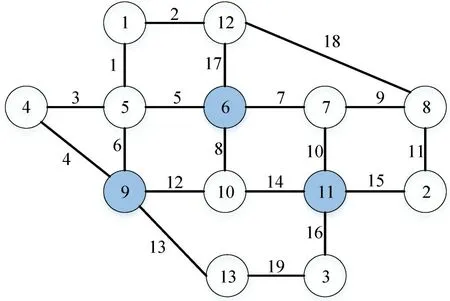
图4 Nguyen-Dupius路网Fig.4 Nguyen Dupius road network

每个站点分别具有2个充电桩，假设充电站各时段总功率约束及购电价格如表3所示。

表3 充电站各时段总功率约束及购电价格Table 3 Total power constraints and purchase prices of charging stations at different time periods

随机在路网中生成15 个电动汽车用户信息，其中，通勤出行类用户3个，计划出行类用户3个以及9 个临时充电用户，具体信息如表4～表6 所示。其他模型相关参数取值及单位如表7所示。

表4 通勤出行类电动汽车用户信息Table 4 Commuter electric vehicle user information

表6 临时充电类电动汽车用户信息Table 6 Temporary charging electric vehicle user information

表7 模型参数取值Table 7 Model parameter values

(2)协同充电结果分析

经计算得出，总收益为408.1 元，调度成本为10 元，各充电站充电桩的运行状态如图5 所示，数字表示在时段功率约束下充电桩的输出功率，S表示充电站(Station)，P 表示充电桩(Pile)，例如，S3P2表示第3 个充电站的第2 个充电桩。图中，不同颜色深度代表不同车辆。

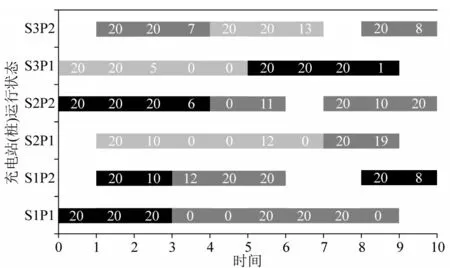
图5 调度优化后充电桩运行状态Fig.5 Operation status of charging station after scheduling optimization

对比不进行车辆调度的情况，计划出行类用户仅前往距离最近的充电站进行充电，此时，考虑两种不同的充电策略，第1 种，是充电站在功率约束下，对所接受充电的车辆必须充至用户要求电量；第2种，是充电站在功率约束和充电桩可用性下尽量多充电，但不一定能够达到电动汽车用户所需求的电量。通过计算，两种充电策略下，充电站的收益分别为249.9 元和353.4 元，分别服务车辆10 辆和13辆。站点充电桩运行状态如图6和图7所示。

图6 第1种充电策略下充电桩运行状态Fig.6 Operating status of charging station under the first charging strategy

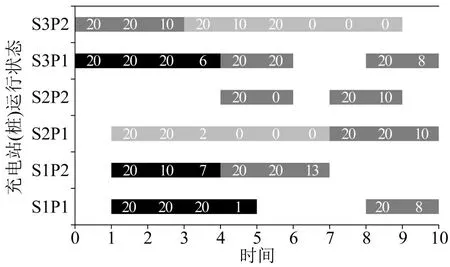
图7 第2种充电策略下充电桩运行状态Fig.7 Operating status of charging station under the second charging strategy

对比不进行电动汽车用户充电调度下的两种充电站充电策略，结果证明，所提出的协同充电调度是有效的，通过经济激励调度部分电动汽车选择合适的充电站，能够从时间和空间维度上协同充电需求，有助于缓解充电资源供给与充电需求之间的时空矛盾，充分利用充电资源，并提高充电站整体收益。

4.2 重庆市南岸区案例分析

(1)数据基础

以重庆市南岸区部分路网为例，提取其骨干道路，并划分路网节点及路段，得到具有236 个节点和340个路段的路网，如图8所示。

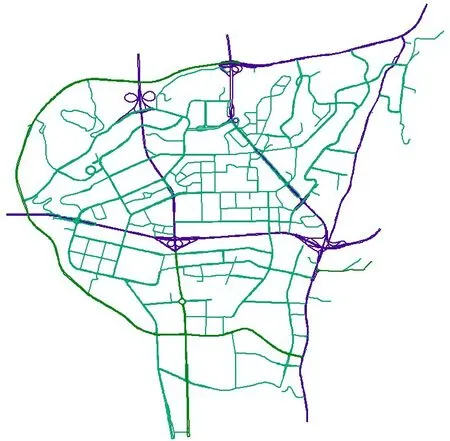
图8 重庆市南岸区部分区域路网骨架Fig.8 Skeleton map of road network in some areas of Nan'an District,Chongqing City

路网中选取10个充电站，仿真测试时间段为8:00-19:00，每隔15 min为1个时间段，共48个时间段。随机在路网中生成不同出行类型的电动汽车用户信息。设置最大求解时间为7200 s，其他模型相关参数在文献[4，8，17，21，25]研究基础上，取值及单位如表8所示。

表8 模型参数取值Table 8 Model parameter values

(2)不同规模下的求解结果

为验证所提算法对模型求解的有效性和实用性，在重庆市南岸路网中选取多个热点地区生成电动汽车出行充电需求，分别在不同规模大小和计划出行类用户数量下进行仿真实验，为直观的表达协同调度对站点收益的影响，对比无序充电，以站点收益的提升率B作为协同充电的收益提升百分比指标，即

式中：B为通过调度站点收益提升的百分比；Zu为无序充电下站点总收益；Zs为采用本文所提调度策略后的站点总收益。通过计算Zs与Zu的差值在Zu的占比表示站点收益提升百分比，站点收益提升百分比B的值越大，表示协同充电调度策略所发挥的效果越好，站点收益提升的越多；反之，站点收益提升百分比B的值越小，站点收益的提升越少。不同规模算例的计算结果如表9所示。

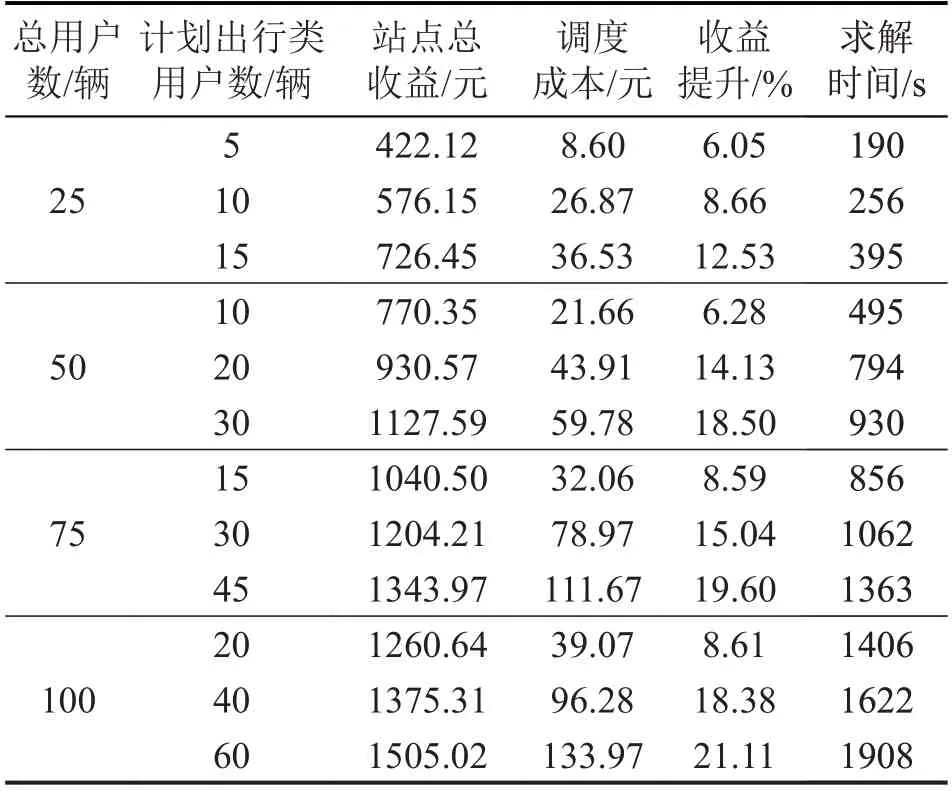
表9 不同规模下的求解结果Table 9 Solution results at different scales

对比不同规模的算例求解结果，随着计划出行类用户在总电动汽车用户数量中的占比增多，调度成本不断上升，同时，站点收益和收益提升的百分比不断上升，证明对计划出行类用户的充电调度是有效的。同时，在相同计划出行类用户占比下，随着总用户规模增加，收益提升的百分比也增大，原因是较大规模电动汽车协同充电中，站点可以更好地协调充电功率，利用峰谷电价获得更高的充电运营收益。

改进遗传算法的收敛情况以迭代过程中解的最优适应度的变化情况为例说明，如图9所示。可知，算法收敛速度较快，且收敛性较好。

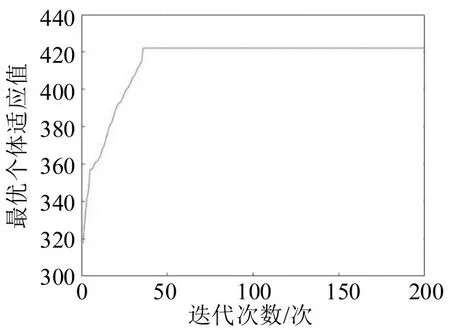
图9 算法迭代变化情况Fig.9 Algorithm iteration changes

4.3 敏感性分析

(1)绕行补偿系数m对调度结果的影响分析

为诱导电动汽车用户服从充电调度，充电站给予绕行充电的用户一定绕行补偿。模型中假定电动汽车用户一定服从充电调度。然而，现实中不同用户的充电偏好不同，用户服从调度的心理补偿价格不一，为保证公平性，在相同路线中均给予统一的绕行补偿。从站点盈利的角度来看，充电站给予的绕行补偿是调度运营的成本之一，为探索不同单位绕行补偿对充电站的决策影响，设计不同大小的绕行补偿参数，观察站点的收益和充电服务车辆数变化。设置绕行补偿系数参数m的变化范围为[0.50,2.75]，其他参数不变，调度结果如表10所示。

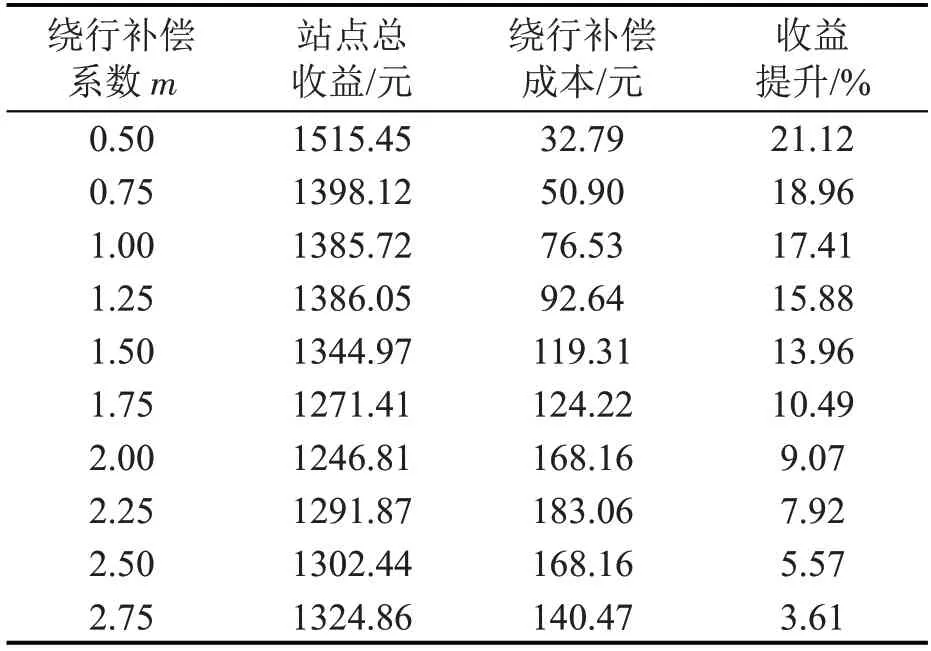
表10 不同绕行补偿下调度优化结果Table 10 Optimization results of scheduling under different detour compensations

观察发现，无论绕行补偿系数在[0.50,2.75]的范围内如何变化，相比于电动汽车的无序充电，对电动汽车进行协同充电调度是有效的。随着绕行补偿系数增大，收益提升的效果逐渐减弱、调度补偿成本先增后减，原因是调度补偿作为站点运营和调度的成本之一，补偿成本增高会导致站点总收益减少，充电站主动进行调度的积极性会降低。充电站运营商偏向于不进行充电调度或调度到附近的站点，导致部分临时车辆无法充电，使得总充电量减少，同时，无法发挥车辆在时间和空间维度的调度效果。

(2)分时电价对站点的激励效果分析

充电站购电价格是影响站点收益的关键因素之一，电网为了减少电力负荷波动，通过使用分时电价政策激励充电站在电力波谷为电动汽车充电，在用电高峰期向充电站收取较高的电费，而在用电低谷期收取较低的电费。充电站也可以向电动汽车用户提供分时电价以改变不同时段充电需求数量，在实验中，采用固定电力销售价格的原因是分时电价可以改变特定时段充电需求数量的多少，从充电供需的角度实现削峰填谷。然而，在充电需求已知，且不能改变的情况下，分时电价所发挥的作用十分有限。充电站的收益主要取决于向电动汽车用户售电价格与从电网购电价格的价差。

同时，充电站的用电受制于电动汽车在充电站中的停留时间，为探究分时电价对站点充电功率协调的激励效果，设计不同的分时电价和电动汽车出行类型比例下的协同充电调度实验，通过站点收益和电动汽车充电服务率对比分时电价对电网削峰填谷的效果。

观察表11，当电网向站点销售电力的低谷电价(0.3 元·度-1)不变时，随着高峰电价的增长(0.5～0.8元·度-1)，购电成本不断上升，导致充电站收益下降。同时，电网峰谷价差的增大，使得站点调度车辆在低谷期充电的积极性增加，调度成本增加和站点的服务率增加。当电网向站点销售电力的高峰电价(0.9元·度-1)不变时，随着低谷电价的增长(0.4～0.7元·度-1)，电网峰谷价差的减小，使站点调度车辆在低谷期充电的积极性减弱，调度成本减少，站点的服务率降低。

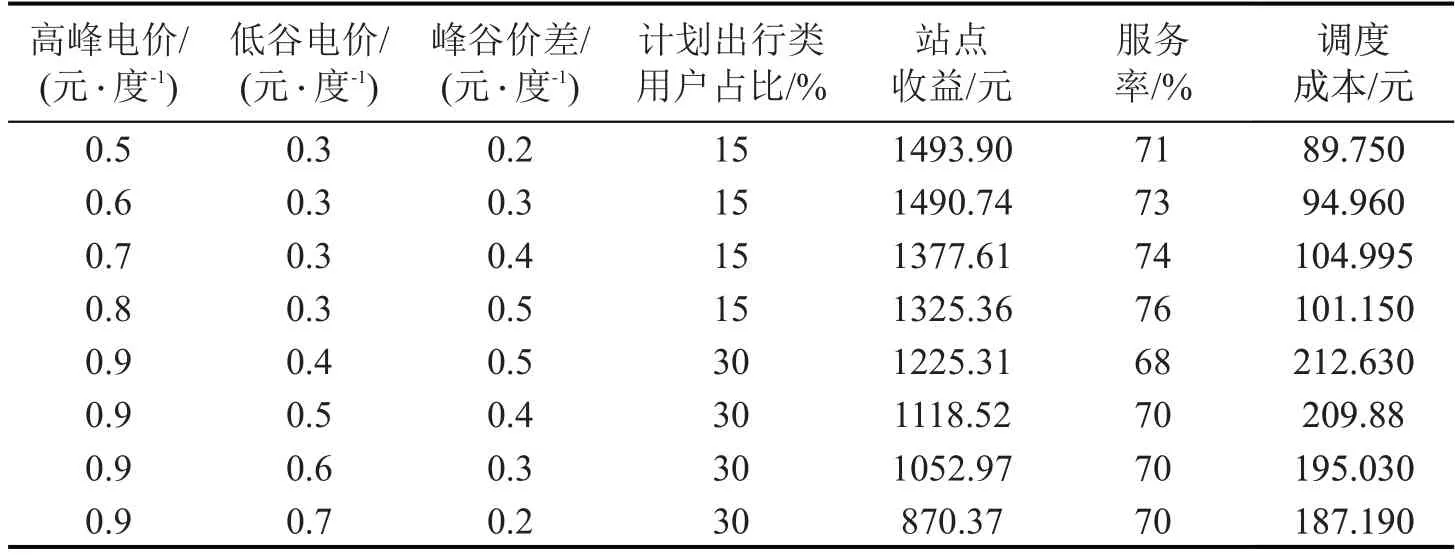
表11 不同电价调度优化结果Table 11 Optimization results of different electricity price scheduling

对比不同电价下电动汽车协同充电结果，证明峰谷电价差越大，站点主动实施充电调度的积极性越高，站点所服务的车辆数越多，电网可以通过提高峰谷价差激励站点主动实施调度和时段充电功率的协调分配，提高站点服务率，并缓解电网负载波动。

5 结论

针对充电需求与供给在时空维度下的不匹配现象，在分析电动汽车用户出行类型的基础上，从站点盈利视角建立电动汽车协调充电调度优化模型，并设计改进优化算法，在经典路网和现实路网中开展算例测试，结果表明：

(1)电动汽车协调充电调度能够从时间和空间维度上协调充电供需，缓解充电资源供给与充电需求之间的时空矛盾，提高充电资源利用率和站点收益。

(2)随着调度补偿力度增大，站点总收益减少，充电站主动进行调度的积极性会降低，收益提升的效果逐渐减弱。

(3)电网通过提高电力峰谷价差，可以激励充电站主动实施充电调度和时段充电功率的协调分配，提高站点服务率并缓解电网负载波动。