基于运载能力的铁路集装箱中心站轨道吊与集卡协同优化
常祎妹,汪洋,朱晓宁
(1.北京物资学院,物流学院,北京 101149;2.北京交通大学,交通运输学院,北京 100044)
0 引言
集装箱在国际和国内商品流通中发挥着重要作用,且一直受到国家和地区政策的支持与重视。铁路集装箱中心站(简称中心站)作为专业办理集装箱装卸和转运业务的场站,是集装箱专列和中欧班列等集装箱列车的组织节点。随着我国“一带一路”的建设和中欧班列开行数量的不断增加,提高中心站作业组织效率成为提升铁路集装箱运输服务质量的关键,因此,需要更加细致合理的研究铁路集装箱中心站的装卸设备和堆场空间等资源的智能调度分配和运输组织协同优化问题。
目前,关于铁路集装箱的研究多数集中于集装箱班列、集装箱多式联运路径选择和中欧班列等方面,对于铁路集装箱中心站的装卸设备调度问题研究较少。当前,国内外学者更加关注集装箱码头与铁水联运集装箱港口的集疏运作业活动,通常以减少作业完成时间和低碳低能耗等为目标进行研究。但是,由于集装箱码头的运作方式、场站布局及作业设备存在着差异,现有的研究成果很难直接运用解决中心站的运作问题。目前,在针对中心站装卸设备作业优化方面,周勇等[1]针对铁路集装箱中心站轨道吊协同装卸调度问题,考虑多轨道吊间的作业干涉和安全距离约束,建立目标函数为最小化集装箱完工时间的混合整数规划数学模型。王小寒等[2]考虑作业效率与均衡问题,协同轨道吊与集卡进行装卸作业优化研究,并合理决策多轨道吊的作业区域。赵睿年[3]研究基于工作量动态划分轨道吊作业范围的“轨道吊-集卡”装卸工艺,采用同步转运策略和混合装卸策略研究分析轨道吊和集卡协同作业。
在集装箱码头设备协同优化的研究中,梁承姬等[4]针对双40 ft 岸桥的工作特点,以岸桥延迟时间、集卡空驶时间及任务对的时间差的加权和最小为目标,建立岸桥集卡的协同调度模型。HOP等[5]研究码头起重机和堆场卡车的集成调度问题,提出一种自适应粒子群优化算法。SKAF等[6]研究单台码头起重机和多堆场卡车的调度问题,旨在减少船舶在码头上的停靠时间,以岸桥作业完成时间最短为目标,建立模型求解。OLADUGBAL等[7]面向双自动堆垛起重机在自动化码头的作业,提出一种基于改进的约翰逊算法,优化双自动堆垛起重机的调度。刘文茜等[8]基于析取图设计4 种邻域算子,通过变邻域禁忌搜索算法求解针对轨道门吊混合装卸模式下的轨道门吊、集卡及场吊协同作业问题。YUE等[9]研究多个靠泊船舶、侧装块和端装块之间的码头起重机、堆场起重机和自动导引车之间的区块分配和综合调度,考虑同时靠泊的多艘船舶的进库、出库和转运集装箱。RUF等[10]研究解决铁水联运模式下双层列车的集成负载规划和排序问题。LIU等[11]研究基于海铁联运集装箱码头新建的U型堆场布局下的堆场起重机与自动引导车之间的集成调度。常祎妹等[12]建立以装卸过程总完成时间最短为目标的龙门吊、集卡和场桥的协同调度问题的混合整数规划模型,并设计改进的多层遗传算法求解模型。田宇等[13]针对自动化集装箱码头装卸过程中,双循环自动导引车和场桥的调度问题,分别设计基于“最早可获得时间”和“最短路径”启发式规则的遗传算法进行求解。
在以上的设备协同优化研究中,多数是以单一规格的集装箱为任务对象,仅考虑20 ft 或40 ft 集装箱的一种,在真正的实践过程中,存在集卡同时运输两个集装箱的情况。目前,国内学者孔灵睿[14]研究基于集卡运载能力的集装箱码头集卡调度问题,根据岸桥吊具的可伸缩性及集装箱在船上的位置情况对集装箱进行配对,进而协同优化集卡指派、提箱顺序、集装箱配对及配对集装箱在堆场的配送顺序,得到最优集卡运输序列和最小化卸箱作业时间。但是,这种集装箱配对模式实际上简化了问题的复杂度,并且文中并未考虑集卡与其他设备的协同优化,从全局角度优化集装箱的装卸作业。因此,本文主要研究铁路集装箱中心站不同设备(集卡-轨道吊)的协同优化问题,并引入集卡“一车两箱”运输模式。此外,集卡进行不同集装箱运输决策时,不考虑集装箱预配对的情况。
1 问题描述
在以往研究的集卡“一车一箱”运输模式场景中,集卡在铁路作业区装载一个集装箱后,直接将集装箱运输至目标堆场进行卸载作业,并且在任务箱卸载完成后,返回到铁路作业区继续完成集装箱的装载任务。但是,在本文研究的集卡“一车两箱”运输模式下,如图1 所示,集卡的作业过程为:首先,集卡到达第1 个任务位置,等待轨道吊进行装箱作业;然后,完成第1个集装箱装载后,再行驶至第2 个任务位置等待装箱;接着,集卡在装载完两个集装箱后,移至目标堆场进行卸载作业;最后,在完成两个集装箱的卸箱作业后,返回铁路作业区继续装载。
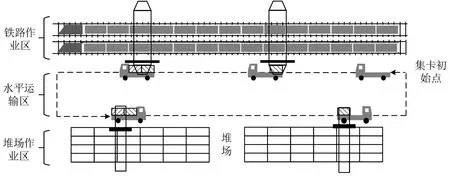
图1 集卡“一车两箱”作业Fig.1 Schematic diagram of"one truck with two containers"operation of a container truck
根据上面的描述可知,集卡“一车两箱”模式相较于“一车一箱”模式在进行两个连续20 ft 集装箱任务的作业过程中,集卡作业完成时间缩短了一段在堆场卸载的时间加上集卡运输的时间,如图2所示。
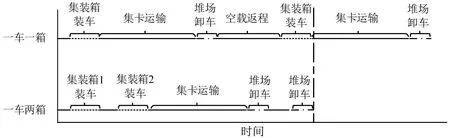
图2 不同模式作业完成时间对比Fig.2 Comparison of operation completion time of different modes
1.1 轨道吊作业
以出口集装箱为例,轨道吊作业以集装箱从班列上吊起为开始和以集装箱吊装在集卡上为结束。在轨道吊的作业中,列车的长度和集装箱的位置会对轨道吊作业的走行时间产生影响。轨道吊在吊起和放下集装箱的速度应当保持匀速,以保证作业的稳定。由于多个轨道吊是在同一轨道上同时进行作业,任一轨道吊之间不可以相互跨越,并考虑轨道吊同时作业时的安全距离。因此,本文既考虑轨道吊作业时的水平移动时间和操作集装箱时间,又考虑轨道吊的安全作业距离和位置约束。
1.2 集卡作业
在单向作业场景下,集卡的作业序列由轨道吊的作业序列决定,而集卡的走行时间与集装箱目标箱位的位置有关。“一车两箱”模式下,集卡完成两个集装箱任务相比于“一车一箱”模式节省了一段空驶返程的时间。但同时,“一车两箱”运输模式下,会延长一次作业的完成时间,导致轨道吊产生等待时间。因此,协调好集卡与轨道吊的等待关系,以及集卡运输两个集装箱的目标箱位,可以缩短集卡“一车两箱”运输模式整个的作业完成时间。
在以往的协同作业问题中,集卡只需负责将集装箱运输至堆场,而装卸顺序由轨道吊作业序列决定,但在“一车两箱”运输模式下,还需要考虑某一集卡在某一运输任务中是否同时运输两个集装箱,且同时运输哪两个集装箱。轨道吊单次只能操作一个集装箱,因此,当集卡同时运输两个集装箱时,需要考虑继续等待同一轨道吊卸载第2 个集装箱或行走至后一个轨道吊装载第2 个集装箱。如果只装载一个集装箱,可以装载一个40 ft或一个20 ft的集装箱。当集卡将集装箱运输至堆场时,按照最短距离原则判断配送顺序。基于以上分析,集卡面临的决策如图3所示。

图3 集卡作业模式决策流程Fig.3 Decision-making process of container truck operation mode
综上,本文主要研究基于集卡“一车两箱”运输模式下,轨道吊与集卡的协同调度优化问题,从而确定最优轨道吊的作业序列、集卡的作业序列及作业完成时间。
2 模型构建
2.1 模型假设
为方便建立数学模型,本文提出以下4 点假设:
(1)不考虑集卡运输路径上的堵塞问题;
(2)只考虑单向作业模式;
(3)不同尺寸的集装箱数量比已知;
(4)集卡初始位置不在铁路作业区。
2.2 符号说明
I——待卸集装箱作业任务集合,i,i′∈I;
I20,I40——20 ft集装箱任务集合与40 ft集装箱任务集合,I20,I40∈I;
L——轨道吊集合,l,l′ 为轨道吊索引,l,l′∈L;
K——集卡集合,k为集卡索引,k∈K;
di——待卸集装箱在列车上,从列车首端开始依次编号1,2,3,…后,集装箱i对应在列车的位置编号;
gi——轨道吊从列车首端开始依次编号为1,2,3,…后,轨道吊l所对应的编号;
——集卡在铁路作业线装载任务箱i后,移动到任务箱i′处的时间;
——集卡在堆场卸载任务箱i后,移动到任务箱i′处的时间;
γ——集卡到达堆场后,集装箱被卸离集卡的时间;
——轨道吊对集装箱i作业结束的时间;
——集卡运输集装箱i并完成堆场卸车的时间;
——集卡为完成连续的集装箱作业任务i,i′,所产生的等待时间;
M——一个很大的正数;
——0-1决策变量,判断是否由轨道吊l对集装箱i进行操作;
——0-1 决策变量,判断是否由集卡k对集装箱i进行操作;
——0-1 决策变量,判断集装箱i与i′是否同一台轨道吊l操作,且集装箱i与i′是前后连续作业;
——0-1 决策变量,判断集装箱i与i′是否被同一集卡k操作,且集装箱i与i′是前后连续作业;
——0-1 决策变量,判断集装箱i与i′是否同时被两个轨道吊操作;
mii′——0-1 决策变量,判断集装箱i与i′是否由同一辆集卡同时运输;
δii′——0-1 决策变量,判断集装箱i与i′是否由同一辆集与轨道吊作业。
2.3 模型构建
(1)目标函数
本文以优化集装箱铁路中心站作业设备调度,提高装卸效率为目标。对一次装卸任务来说,要以尽可能短的时间完成,因此,将总作业完成时间最小化作为模型的目标。如图2所示,在“轨道吊-集卡”协同调度问题中,作业完成时间即是集卡完成最后一个集装箱的时间加上堆场卸车时间,因此,目标函数为
(2)约束条件
通过分析装卸作业流程,对作业过程当中的作业接续关系、作业完成时间关系及作业安全空间位置这3个方面设置如下约束。
①作业接续关系约束
式(2)表示每个集装箱均只有1 台轨道吊对其操作;式(3)表示每个集装箱均只有1辆集卡对其操作;式(4)和式(5)表示决策变量之间的关系;式(6)表示在每台轨道吊的作业中,每个集装箱均只有一个前续后续集装箱;式(7)表示在每辆集卡的作业中,每个集装箱均只有一个前续后续集装箱;式(8)表示40 ft的集装箱只能由1辆集卡单独运输;式(9)表示一个20 ft的集装箱最多只能有一个另一个20 ft集装箱一起配送;式(10)表示,如果两个集装箱是由一个集卡同时运输,则一定是紧前紧后的任务。
②时间关系约束
式(11)表示当轨道吊连续装卸2 个集装箱时,后一个集装箱的作业开始时间要晚于前一个集装箱的作业结束时间加空驶至后一集装箱位置的时间。式(12)表示当集卡为装载2个20 ft集装箱i,i′,且为相同轨道吊l进行装卸时,集卡开始作业集装箱i′的时间要晚于集卡开始作业i的时间加上轨道吊操作i的时间,当为不同轨道吊进行装卸时,集卡开始作业集装箱i′的时间要晚于集卡装载集装箱i后加上集卡行驶至i′的时间与等待时间;当集卡为装载一个集装箱时,集卡开始作业集装箱i′的时间要晚于集卡结束i的时间加上空驶返回时间与等待时间。式(13)表示当集卡为装载两个20 ft集装箱i,i′时,轨道吊开始作业的时间要晚于集卡装载集装箱i后行驶至i′的时间;当集卡为装载一个集装箱时,轨道吊作业的开始时间要晚于集卡完成集装箱i的作业完成时间加上空驶回任务集装箱i′的时间。式(14)表示,集卡开始作业集装箱i的时间要大于轨道吊结束集装箱i′作业的时间。式(15)表示轨道吊作业集装箱i的结束时间等于开始时间加上操作时间。式(16)表示当集卡只运输一个集装箱i时,作业结束时间等于开始时间加上水平运输至堆场的时间加上堆场卸车的时间;当集卡运输2个集装箱时,作业结束时间为集装箱i′的开始时间加上水平运输至堆场的时间与堆场卸车的时间。式(17)表示当集卡运输两个集装箱时集装箱i′的作业结束时间等于集装箱i的结束时间加上水平运输至集装箱i′堆位的时间与堆场卸车的时间。式(18)表示若当集卡只运输一个集装箱时,完成前一集装箱的作业任务并已行驶至后一作业位置,若此时轨道吊还未结束任务,集卡产生等待时间;若集卡同时运输两个集装箱时,装载一个集装箱后至另一个轨道吊装卸时轨道吊还未结束任务,集卡产生等待时间。
③作业安全约束
式(19)表示由于轨道吊之间的不可跨越性,因此,当两台轨道吊同时作业时,应满足安全位置约束,即较小号的轨道吊应该处于编号较小的集装箱列车装车位置;式(20)表示轨道吊安全位置关系约束,两台轨道吊不能对相邻位置的集装箱同时作业。
3 算法设计与模型求解
孔灵睿等[14]已证明,基于运载能力的集装箱码头集卡调度问题是NP 完全问题,无法利用精确算法求解。因此,需要利用智能算法进行求解。由于遗传算法具有隐形并行性,并在求解顺序编码优化问题上具有明显优势,故本文选择遗传算法求解模型。但是,遗传算法的局部搜索能力较差,尤其是在优化后期搜索效率较低,容易陷入局部最优,为解决此问题,本文将模拟退火算法用于遗传算法的演化过程中进行局部搜索和优化。因此,本文提出的遗传模拟退火算法流程如图4 所示,图中,G为当前迭代次数,M为最大迭代次数,Ti为当前退火温度,Tmin为指定的最小退火温度,φ为模拟退火系数。
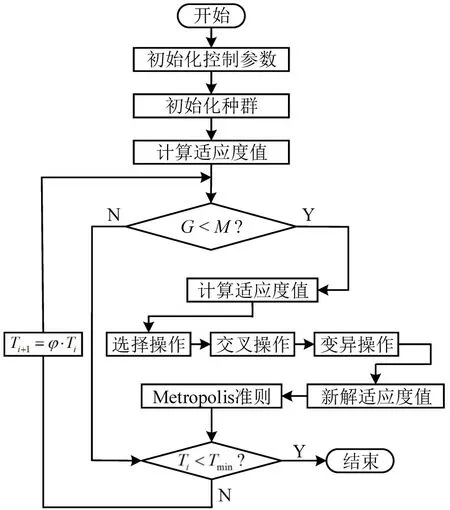
图4 遗传模拟退火算法流程Fig.4 Flow chart of genetic simulated annealing algorithm
3.1 编码设计
本文采用二进制编码方式,假定一个字符串长度为5,装卸任务数量为n,则一条遗传算子的长度为5n。在模型进行仿真求解时,需要将二进制编码转换为十进制。遗传算子编码及转换如图5 所示,其中,遗传算子的长度为5,装卸任务数量n=3。

图5 遗传算子编码及转换示意Fig.5 Genetic operator coding and transformation scheme
在本算法中,当二进制编码转换为十进制编码后,再根据每位上数字的大小进行排序确定集装箱的作业序列。因此,图5 中,编码转化后的结果为“3-1-2”,编码中每个数的位次(由左至右,从1开始)同时,也是相对应的集装箱的编号,故该编码所表示集装箱的待卸载顺序为“2-3-1”。
3.2 适应度函数
本文的优化目标是集卡完成最后一个任务的时间最短,因此,本算法中将适应度函数设为目标函数值的倒数,即
3.3 选择操作
本文采用轮盘赌的方式进行遗传选择操作。当个体的适应度值越大,其在轮盘中分配到的角度就越大,因此,被选中的概率就越大。轮盘赌个体选择概率pselect为
式中:fi为第i个体的适应度值;N为个体总数。
3.4 交叉操作
本文在算法中采用两点交叉模式,具体交叉示意如图6所示。
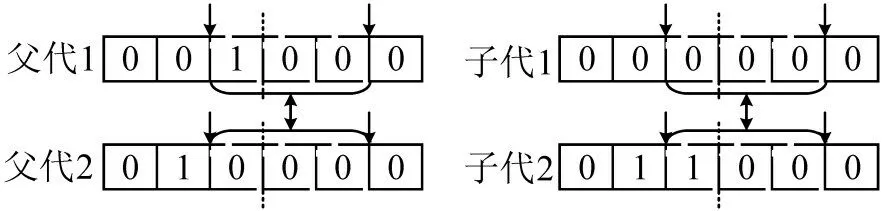
图6 交叉操作示意Fig.6 Cross operation scheme
3.5 变异操作
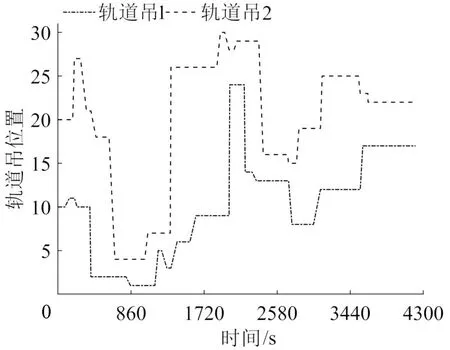
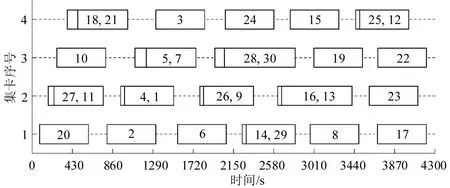
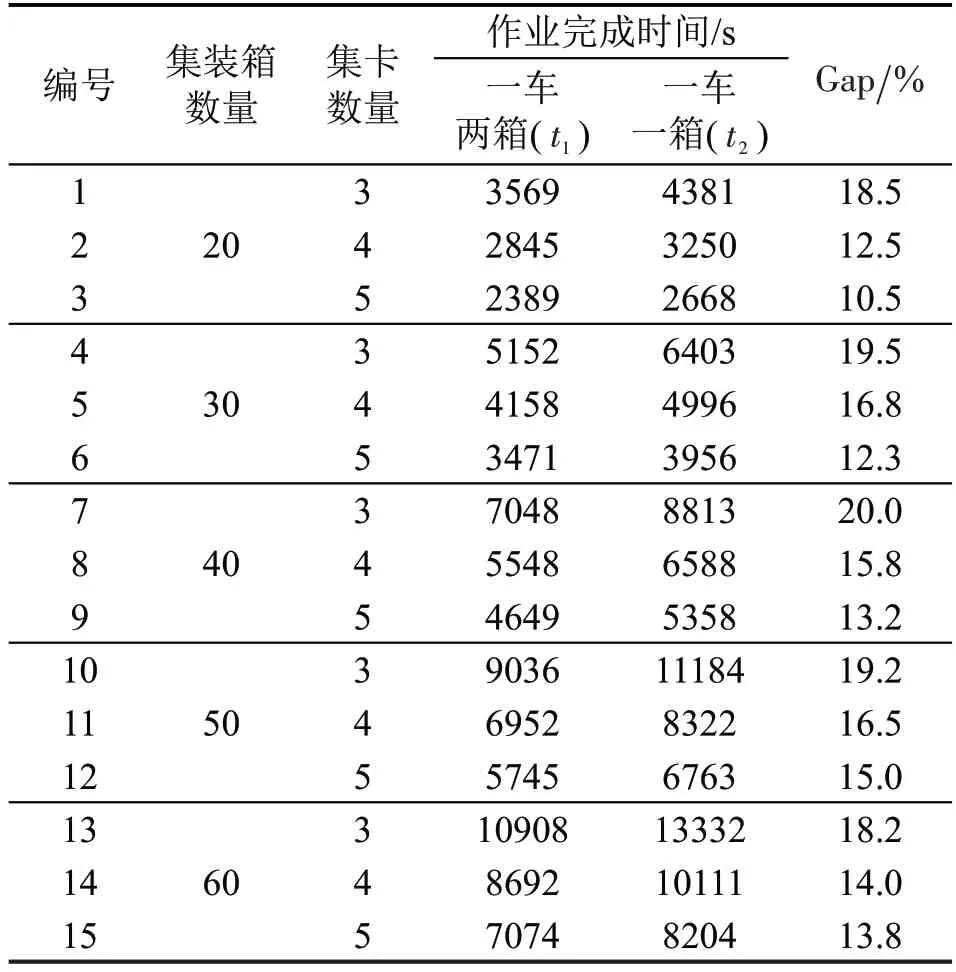
本文在算法中采用基本位变异策略,设第m位的变异概率为pm,r为一个随机数,r⊂[0,1],若r 在完成遗传操作后,为解决算法陷入局部最优的问题,再利用模拟退火算法进一步优化。 (1)Metropolis准则 由于遗传算法容易陷入局部最优,因此,在遗传算法中加入Metropolis 准则,帮助算法跳出局部最优。fi′与fi分别表示新个体的适应度值与当前最优适应度值。在温度T下,若新解的适应度值小于等于当前最优解,则生成一个随机值r⊂[0,1],若此时,r (2)退火操作 退火函数为 式中:ρ⊂[0,1]为退火系数,退火系数的选择是算法的收敛性与效率的重要影响因素。 由于本文编码设计仅表示集装箱待卸载顺序,但并未表明待卸载集装箱对应哪个轨道吊,因此,在模型求解时设计轨道吊任务分配策略,将集装箱任务分配给各轨道吊。为更清楚地描述轨道吊的任务分配流程,给出设计流程中的符号说明,如表1所示。 表1 轨道吊任务分配流程中的符号说明Table 1 Description of symbols in orbital crane task assignment process 根据产生的集装箱作业序列,按如下流程将作业任务序列分配给各轨道吊。 Step 1 输入集装箱作业序列。 Step 2 判断已完成任务数量是否等于总任务数量,若是,则退出分配;若否,则转到Step 3。 Step 3 搜索任务集合,检索出未被分配轨道吊与未在执行中的任务集合τ,转到Step 4;若τ为空集,转到Step 2。 Step 4 检索空闲的轨道吊。若无空闲轨道吊,转到Step 6。若空闲轨道吊为l1,且,在τ中检索符合条件:集装箱所在位置的序列最小的集装箱i作为待装卸任务,转到Step 7。若空闲轨道吊为l2,转到Step 5。 Step 5 若空闲轨道吊为l2,且,在τ中检索符合条件:集装箱所在位置pi>+2 的序列最小的集装箱i作为待装卸任务,转到Step 7。 Step 7 更新该轨道吊的时间和位置信息,转到Step 2。 本文以长度为10 的遗传算子解码为示例,具体步骤如下: (1)输入二进制编码转化后的编码,得到集装箱作业序列为a=[3,6,1,4,7,5,2,10,9,8]。 (2)根据任务分配方式,获得每个集装箱分配到的轨道吊的编号,如图7所示。 图7 集装箱作业序列与作业轨道吊对应图Fig.7 Corresponding diagram of container operation sequence and operation rail crane (3)输出集装箱作业顺序与各集装匹配的轨道吊,即轨道吊1作业序列为[3,1,4,2],轨道吊2作业序列为[6,7,5,10,9,8]。 (1)算例参数设置 本文以集装箱任务数量为基础,设置不同规模的算例实验。算例参数设置如表2所示。 表2 算例参数设置Table 2 Example parameter setting 所有实验得到的结果都是对比集卡“一车两箱”与“一车一箱”模式下的协同作业方案。实验均在3.20 GHz Intel(R)Core(TM)i5-11320H CPU和内存16 GB 的计算机上运行,通过MATLAB R2022a进行编码并实现。此外,所有实验采用的遗传模拟退火算法中参数设置为:初始解数量为100,交叉概率为0.7,变异概率为0.01。算法执行1000 次停止迭代,并对每种算例进行10次实验取平均值。 (2)确定退火系数 通常退火系数对算法求解的收敛性与效率会产生影响,故需选择合适的退火系数。本文将ρ取值为0.99,0.95,0.90,0.85,0.80,分别以同一算例进行实验,结果如图8所示。 由图8 可知,当ρ取值越小,算法收敛速度越快,同时,也可能导致算法过早收敛至较差的局部最优解。在5个取值中,当ρ=0.95 时,算法收敛性最优,尽管收敛速度并不是最快,但是,可以使算法求得更优的解。因此,后续的实验中,将ρ的值设置为0.95。 首先,为验证算法的有效性,选取5 个小规模与5 个大规模算例进行实验,其中,20 ft 集装箱与40 ft集装箱数量比设置为3∶2,结果如表3所示。 表3 不同规模下协同作业模式对比Table 3 Comparison of collaborative working modes under different scales 由表3 可知,相比于集卡“一车一箱”模式,集卡“一车两箱”模式下,作业完成时间平均缩短了12.9%。其中,在小规模算例中,随着集装箱数量的增加,集卡“一车两箱”模式下的协同方案优势更加明显。这是由于当集装箱数量规模较小时,在整个作业过程当中,集卡单次运输两个20 ft集装箱的次数较少,总节省的时间有限。而在大规模算例中,随着集装箱数量的增加,优化效率保持在13.2%~12.0%波动,这是由于大规模集装箱场景下,优化空间趋于饱和,因此,优化效率趋于固定。综上,算法能够有效求解铁路集装箱中心站中轨道吊与集卡的协同优化问题。 其次,为对比不同设备在不同模式下的作业情况,选取30个集装箱、2台轨道吊及4辆集卡进行实验,得到轨道吊在不同模式下的作业轨迹,如图9和图10所示,以及集卡的作业序列,如图11和图12所示。其中,图11 和图12 中的每个矩形均代表一次集卡作业任务,矩形左侧代表集卡开始作业的时刻,右侧代表完成任务的时刻,矩形中的数字代表集卡运载集装箱的编号。 图9 集卡“一车一箱”模式轨道吊作业轨迹Fig.9 Rail mounted gantry crane operation track in"one truck with one container"mode 图10 集卡“一车两箱”模式轨道吊作业轨迹Fig.10 Rail mounted gantry crane operation track in"one truck with two containers"mode 图11 集卡“一车一箱”模式下集卡作业序列Fig.11 Container truck operation sequence in"one truck with one container"mode 图12 集卡“一车两箱”模式下集卡作业序列Fig.12 Container truck operation sequence in"one truck with two containers"mode 由图9 和图10 可以看出,轨道吊1 与轨道吊2分别从集装箱10与集装箱20在列车上的位置开始作业。相比于集卡“一车一箱”模式,集卡“一车两箱”模式下的轨道吊作业更加灵活,缩短集卡在运输两个20 ft集装箱时在铁路线的移动时间,总体空驶与等待时间明显减少。同时,集卡“一车两箱”模式下,作业量更趋于均衡,以轨道吊1为例,作业箱数量从14 TEU上升至15 TEU。 从图11 和图12 可以看出,集卡“一车一箱”和“一车两箱”模式下作业完成时间分别为5019 s 与4286 s,Gap 值为14.6%。由于模式的改变,集卡的作业序列也随之发生改变,以集卡3 为例,装卸任务由8 TEU优化为7 TEU。从全局来看,模式转变后,20 ft 集装箱的作业任务均集中于集卡2,而集卡1 以运输40 ft 集装箱为主。此外,在集卡“一车两箱”模式下,集卡运输的总车次由30 减少至21,总车次减少30%。 最后,固定集装箱数量改变集卡数量,研究集卡数量对作业完成时间的影响,设置20 ft集装箱与40 ft集装箱数量比为3:2。求解结果如表4所示。 表4 不同规模算例下作业效率对比Table 4 Comparison of operation efficiency under different scale examples 由表4可知,集卡“一车两箱”模式的平均优化率为15.7%,尤其是集卡数量为3时,作业完成时间差值均高于18%。此外,当集装箱任务量相同时,集卡数量越少,集卡“一车两箱”模式的优势就越明显。因此,当中心站的集卡资源有限时,更倾向于采取集卡“一车两箱”模式。 本文在考虑集卡实际运载能力的基础上,研究在铁路集装箱中心站单向作业场景中,集卡“一车两箱”模式下,轨道吊与集卡的协同优化问题,构建以总作业完成时间最短为目标的数学优化模型,考虑集卡运输不同尺寸集装箱的决策等因素,并设计考虑轨道吊任务分配策略的遗传模拟退火算法,并进行不同规模的实验,实验结果如下: (1)相较于传统模式,集卡“一车两箱”模式下,轨道吊与集卡的协同作业效率更高,作业完成时间平均缩短了13.3%,同时,集卡运输集装箱的尺寸也更集中,以集卡2为例,集卡2由原来装载3个20 ft集装箱变为装载8个20 ft集装箱。此外,集卡运输的总车次减少了30%。 (2)通过研究集卡数量的变化对协同作业的影响,可以发现,当集卡为3辆时,随着算例规模的增大,集卡“一车两箱”模式的作业完成时间相比于传统模式平均减少18%以上,并且在同一算例下,随着集卡数量的减少,“一车两箱”模式协同作业的优势越明显。 (3)将集卡“一车两箱”模式引入集卡与轨道吊协同优化问题中,充分发挥集卡运载能力的优势,通过与轨道吊协同作业,合理地分配作业任务,并得出不同集装箱数量与集卡数量下作业完成时间和作业序列。 (4)本文设计的集卡“一车两箱”模式下的轨道吊与集卡协同优化模型与算法,能够有效求解铁路集装箱中心站单向作业场景下的装卸作业问题,轨道吊与集卡协同作业序列合理,总作业完成时间优于传统“一车一箱”模式。并且当集装箱数量在40~100 TEU之间时,优化效率更佳。3.6 模拟退火操作
3.7 轨道吊任务分配策略

3.8 解码设计

4 算例分析
4.1 算例基本情况
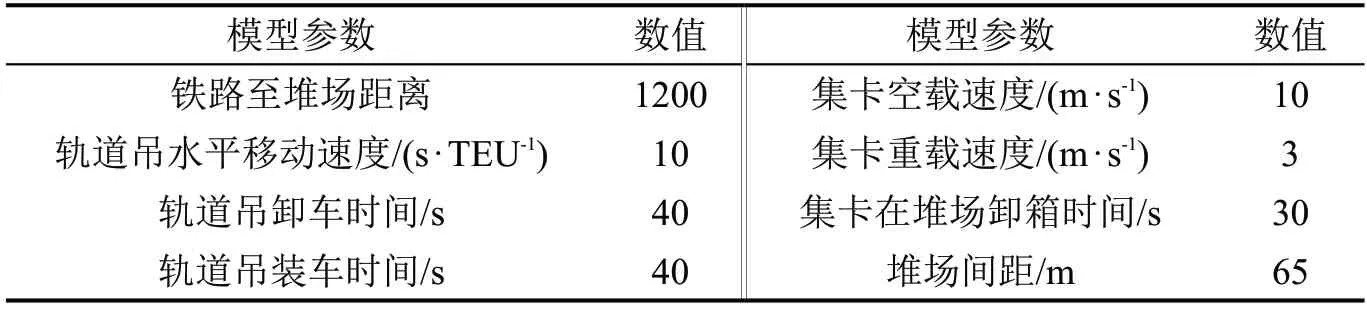
4.2 算例分析



5 结论

