高速列车轴箱轴承载荷反演模型及关键参数优化匹配
唐 嘉, 池茂儒, 杨 晨, 马子魁, 姚雪松, 罗 赟
(1. 西南交通大学 牵引动力国家重点实验室,成都 610031;2. 舍弗勒贸易(上海)有限公司,上海 201800)
轴箱轴承作为高速列车传动系统中的关键部件,在高速旋转的同时还需承受一定负载,一旦发生故障会直接影响行车安全。准确获取轴承的服役边界载荷,对其结构设计与优化、疲劳寿命评估具有重要意义。
关于轴箱轴承载荷特性的研究,主要分仿真和试验两种手段。仿真分析方面,Cheng等[1]利用有限元软件对轴箱轴承进行应力计算和载荷分布计算。查浩等[2-3]建立了包含轴承的车辆-轨道耦合动力学模型,研究了高速动车组轴箱轴承的振动及载荷特征。杨晨等[4-5]通过构建轴承-车辆-轨道-结构刚柔耦合动力学模型,实现对轴箱轴承动态载荷的计算和疲劳寿命的估计。涂文兵等[6]通过建立高速列车轴箱圆柱滚子轴承动力学模型,研究了轴承启动过程中的运动学特性和载荷特性。试验研究方面,刘德昆等[7-8]将轴箱弹簧和转臂传感器化,提出了通过弹簧和转臂载荷来得到轴承载荷的方法。此外,他还对轴承外圈开槽,直接在轴承外圈安装应变片,提出了将轴承传感器化的载荷识别方法,并通过台架试验进行了验证。周高伟等[9-10]进一步研究了轴承外圈应变检测得到轴承载荷分布的方法,并提出了相应的开槽方案。然而,轴承载荷仿真必须已知系统边界输入,很难再现服役过程中的全部工况。同时,受制于测试手段,工程师需要对结构进行特殊工序改装,因而无法长期、普适地采用,很难在车辆线路试验中获得轴承服役载荷。
关于载荷辨识技术,Li等[11-13]提出了基于频谱分解与正则化的时域法以及时域Galerkin法,通过构建不同的函数和矩阵,提高了动态载荷的识别精度和抗干扰能力,此外,他们还提出了一种新的时空耦合分布式动态载荷的稀疏识别方法,使用适当的正交分解,可从时域和空域的角度描述和识别载荷。随着计算机技术的提高,载荷反演技术作为求解结构动力学的第二类反问题,在高速列车上的应用也越来越广泛,为轴承载荷的获取提供了新的思路。Xiao等[14]考虑车桥交互作用,利用卡尔曼滤波算法对铁路桥梁轨道不平顺进行估计。Furukawa等[15]通过车辆垂直加速度预测轮轨力。周亚波[16]和柯飙[17]同样基于加速度分别对轮轨力和轨道谱进行反演。众多学者对高速列车的载荷反演研究大多集中在轮轨上,对轴承的载荷反演却很少,只有少部分学者对此进行过研究,如李春昱等[18]和李振乾等[19]通过建立车辆动力学模型,利用车辆振动加速度对高速列车轴箱轴承载荷进行反演,但他们模型中的力传递关系考虑简单,且没有对滤波参数进行优化和讨论,反演精度和线路适应性不高。
因此,本文针对已有研究的不足,对实际线路运行中难以直接测量的轴箱轴承载荷,提出一种基于卡尔曼滤波原理的载荷反演模型,采用自适应小生境遗传算法对模型中的关键滤波参数开展了优化匹配,利用此方法求得轴承的边界载荷,并与车辆动力学正向计算结果开展了对比验证。
1 轴箱轴承载荷反演模型建立
1.1 基于机理模型的卡尔曼滤波算法
卡尔曼滤波以最小均方误差为准则,采用状态空间模型和递推形式,得到系统状态的最优估计,其状态空间方程的矩阵形式表示如式(1)所示[20]
(1)
方程组如式(2)~式(6)所示
(2)
(3)
(4)
(5)
Pk=(I-KkHk)Pk∣k-1
(6)
式中:x为系统状态矢量;y为系统观测矢量;u为输入矢量;A为系统矩阵;B为输入矩阵;H为输出矩阵;w和v分别表示过程噪声矢量和测量噪声矢量,对应x和y中每个分量的噪声,考虑为分别满足协方差为Q和R的高斯白噪声,二者相互独立且服从正态分布。Q为系统过程噪声矩阵;R为观测噪声矩阵;P为状态量的协方差矩阵;K为增益矩阵;I为单位对角矩阵。
结合式(7)振动微分方程,将其变形整理可得到卡尔曼滤波系统中的系统矩阵和输入矩阵,如式(8)、式(9)所示
(7)
(8)
(9)

采用卡尔曼滤波算法开展轴承载荷估计,还需推导车辆系统各部件运动微分方程,以明确式(8)、式(9)中的质量、刚度和阻尼矩阵。
1.2 垂向载荷反演模型
由于铁道车辆的垂向和横向运动耦合关系不强,且系统中各个状态量间的数量级相差较大,滤波计算时容易发散,所以可分别进行研究。车辆的浮沉、侧滚和点头运动会引起垂向受力变化,横移、侧滚和摇头运动会引起横向受力变化。
将轴箱转臂装置考虑为一个质量体,轴箱与轴承之间的作用力为系统输入,轴承受到的载荷作为输出,只考虑车体、构架与转臂轴箱,建立半车动力学模型。轴承体与轮对的运动作为模型输入激励的产生源,无需体现在模型中,以减少模型误差对轴承反演的影响。
垂向模型中考虑车体浮沉zc、侧滚φc和点头βc,构架浮沉zti(i=1, 2)、侧滚φti和点头βti,轴箱浮沉zbj(j=1, 2, 3, 4, 5, 6, 7, 8),共计17个自由度,建立了如式(10)~(16)所示的车辆垂向运动方程[21-22]。
车体浮沉运动
(10)
车体侧滚运动
(11)
车体点头运动
(12)
构架浮沉运动(当i=1时,j=1~4;当i=2时,j=5~8)
(13)
构架侧滚运动(当i=1时,j=1~4;当i=2时,j=5~8)
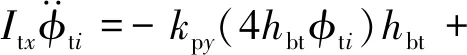
(14)
构架点头运动(当i=1时,j=1~4;当i=2时,j=5~8;当j=1, 2, 5, 6时±取-)
(15)
轴箱浮沉运动(当j=1~4时,i=1;当j=5~8时,i=2;当j=1、2、5、6时±取+)
(16)
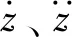
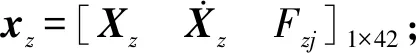
根据卡尔曼滤波原理,对连续系统状态方程离散化,得到如式(17)所示垂向载荷反演模型的离散状态空间方程
(17)
式中,Az=I+AT,Bz=TB,T为采样时间间隔,其中Az和Bz是由式(8)和式(9)在采样间隔T内积分得到的。
1.3 横向载荷反演模型
横向模型中考虑车体横移yc、侧滚φc与摇头ψc,构架横移yti、侧滚φti与摇头ψti,轴箱横移ybj,经推导可得式(18)~(24)所示的车辆横向运动方程。
车体横移运动
(18)
车体侧滚运动
(19)
车体摇头运动
(20)
构架横移运动(当i=1时,j=1~4;当i=2时,j=5~8)
(21)
构架侧滚运动(当i=1时,j=1~4;当i=2时,j=5~8)

(22)
构架摇头运动(当i=1时,j=1~4;当i=2时,j=5~8;当j=1, 2, 5, 6时±取-)
(23)
轴箱横移运动(当j=1~4时,i=1;当j=5~8时,i=2;当j=1、2、5、6时±取+)
(24)
横向离散状态空间方程为
(25)
式中:Ay=I+AT;By=TB。
2 反演模型关键参数优化匹配
在卡尔曼滤波系统中需提前确定3个重要矩阵的参数:初始协方差矩阵P0、观测噪声矩阵R及过程噪声矩阵Q,它们决定了滤波反演效果。P0为状态协方差矩阵P的初值,其取值对滤波效果影响很小,故一般将P0设成近似的单位矩阵。R与传感器测量精确度有关,决定系统观测量的可靠度,取值受观测设备及外界环境影响,通常取较小且不为0的定值。Q由不确定的噪声引起的,决定系统数学模型的精确性,取值对应系统状态量中各元素的方差[23]。
在3个重要矩阵中,Q的取值最为关键,矩阵中的每一项对滤波反演结果都有着“牵一发而动全身”的影响,对其取值可以看作是对卡尔曼滤波系统进行超参数设置。由于缺乏对噪声统计特性的了解,一般依照仿真或经验合理地给出矩阵值,再通过滤波结果调整参数大小,达到最佳效果。这种在仿真过程中不断试验手动调整,分配权重,俗称调谐。然而在多数情况下,卡尔曼滤波参数通过人为设定或手动调整成“正确”的值,难免会影响数据选取的科学性和严谨性。盲目穷举下不仅工作量大,其结果也极不准确和稳定,易造成滤波结果失真。
因此,本章提出了采用自适应小生境遗传算法,针对卡尔曼滤波系统中较难确定的关键参数Q进行优化,获取全局最优的滤波参数值,以期得到更为准确的载荷反演结果。
2.1 关键参数优化匹配方法
自适应小生境遗传算法就是在遗传算法的基础上增加小生境思想[24],引入精英保留策略、自适应交叉和变异算子、自适应小生境距离参数,使算法具有更强的优化性能和稳定性,改善传统遗传算法存在的“早熟”现象,提高全局搜索能力和收敛速度,保持种群多样性。
利用自适应小生境遗传算法对Q进行优化,需结合多体动力学软件SIMPACK和数值计算软件MATLAB。在SIMPACK中建立考虑轴箱轴承的整车动力学模型进行工况仿真并输出数据,在MATLAB中搭建包含卡尔曼滤波系统和遗传算法的嵌套模型,实现载荷的在线估计和参数的在线优化。关键参数优化方法流程图,如图1所示。
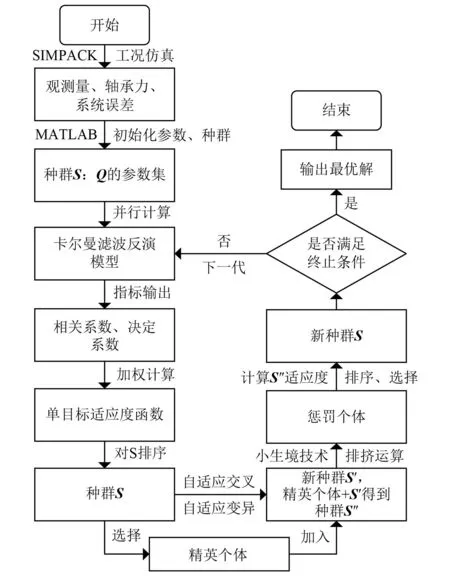
图1 关键参数优化方法流程图
(1) 首先在SIMPACK中进行工况仿真,输出数据并导入至MATLAB中,观测量作为卡尔曼滤波系统的输入数据,仿真得到的轴承力作为滤波系统载荷估计后的对比依据,系统误差对应Q的方差,为自适应小生境遗传算法提供初值,方便以此为基础建立初始化参数和种群。
(2) 在MATLAB中初始化参数,规定遗传代数、精英个体数、惩罚系数、初始交叉和变异概率,作为后续处理的基础。在初始种群中,将过程噪声矩阵Q中的15个状态量分别视为优化参数,进行梯度抽样,得到关于Q的参数集种群S。
(3) 然后将P中的个体带入滤波载荷反演模型中,得到指标结果,该过程利用MATLAB的parallel pool工具包并行计算提高效率。
(4) 本文采用Pearson相关系数和决定系数R2作为反映轴承载荷反演效果的评价指标,观察相关程度与幅值差异,检验结果可靠性。考虑仿真的真实(ture)值与反演的估计(estimated)值,表达式为
(26)
(27)
(5) 为提高计算效率,将车体中8个不同位置的轴承反演评价指标合并为一个整体进行优化,得到一套适用于该车所有轴承的滤波参数。因相关系数和决定系数都是越接近1越好,视两者同等重要,权重各占50%,将多目标函数构建成单目标最大值优化问题,则单目标适应度函数为
(28)
若针对特定工况或轴承,亦可根据实际需求,按单个转向架或单个轴承进行参数寻优,得到各自的优化结果,则式(28)中j=1~4或j=1。
(6) 接着将计算的个体结果排序,用精英保留策略[25]进行选择,避免最优解的丢失,指导算法的进化方向,加快进化速度。对S进行交叉和变异操作得到种群S′,这里的自适应交叉算子和变异算子[26]可依据群体进化信息适时调整各自概率值,加快收敛速度,提高全局搜索和局部快速开发能力,使解更稳定、准确。
(7) 将精英个体加至S′中,得到种群S″,采用小生境技术排挤运算,将个体间的距离判别参数设置为与进化代数有关的动态函数,即动态海明距离[27],对不符合的个体施加惩罚系数,这样既能使种群进化初期保持个体差异,也能在后期使优良个体相似,从而维护种群多样性。
(8) 最后计算S″的适应度,并排序、选择,得到新种群S,循环运算直至达到指定遗传代数,输出结果。
全程不断更新关键滤波参数Q的取值,并计算反演结果,实现在线优化和估计,将代理模型与反演模型结合,通过遗传操作得到最优参数。
2.2 动力学仿真模型
在确定了机理模型和参数优化方法后,还需建立相应的动力学模型进行工况仿真,验证反演模型和优化方法的正确性。在SIMPACK中考虑转臂轴箱轴承,建立轴承-车辆耦合系统动力学模型,实现对轴承动态载荷的计算,其动力学模型示意图如图2所示。

注:①1位轴承;②2位轴承;③4位轴承;④3位轴承;⑤5位轴承;⑥6位轴承;⑦8位轴承;⑧7位轴承
模型中车辆系统由1个车体、2个构架、4个轮对、8个轴箱转臂组成,其结构参数与悬挂参数同半车动力学模型一致。1位轴承对应一位构架一位端左侧,2位轴承对应一位构架一位端右侧,3位轴承对应一位构架二位端左侧,依次类推,定义1~8位轴承位置。
模型中将轮对考虑为柔性,为LMA型踏面,钢轨为CHN60轨,采用FASTSIM算法计算轮轨蠕滑力,轮轨摩擦因数为0.3,设置相应位置传感器来测量反演所需的观测量,施加实测京津轨道谱激励,车速设置为350 km/h沿直线恒速运行。将软件中输出的轴承外载荷作为仿真值,卡尔曼滤波系统中输出的作为反演值,以此进行动力学的对比分析,验证反演效果。
2.3 参数优化结果
根据滤波矩阵的取值原理,令P0=0.1×I43×43,R=1×10-5×I17×17,将SIMPACK中输出的状态量进行方差运算,分别得到垂向和横向Q中各项的初值,以初值为中心建立种群,采用自适应小生境遗传算法分别对垂向和横向进行优化,其目标函数最大值随迭代次数变化如图3所示。
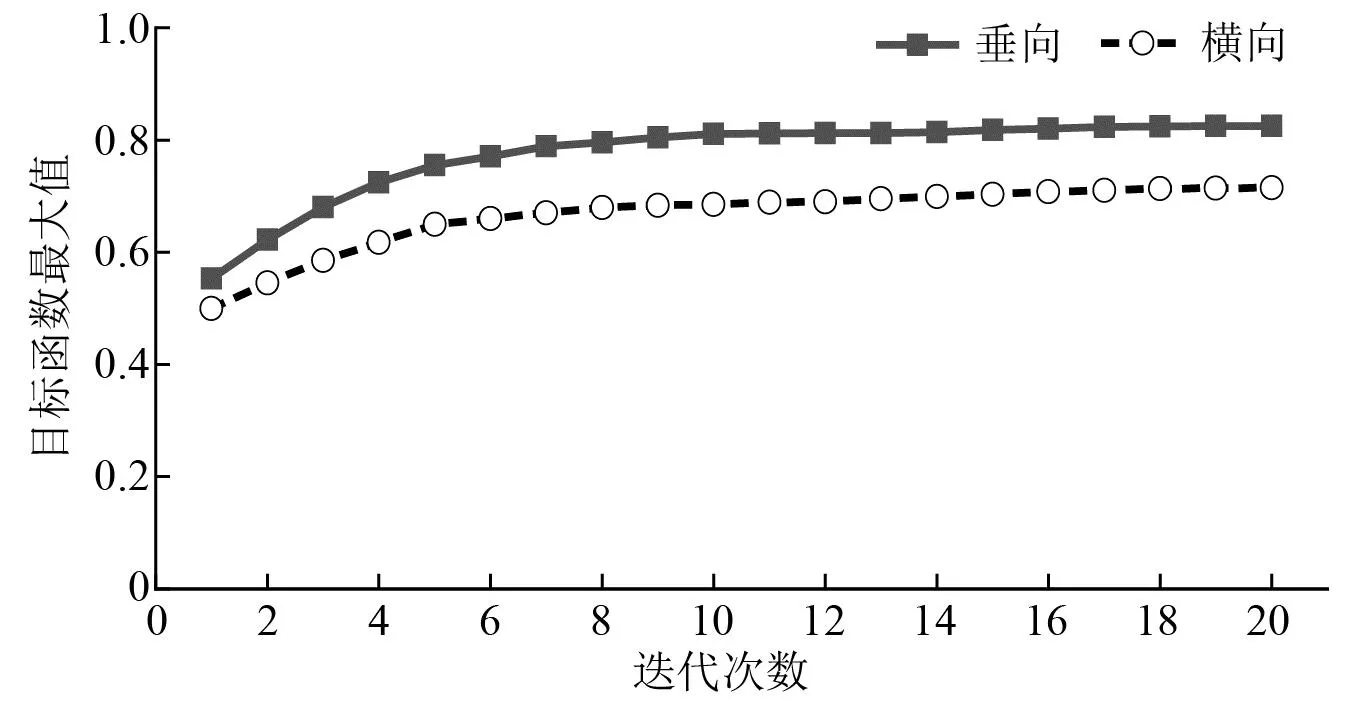
图3 目标函数最大值变化
当各目标函数最大值趋于稳定时,得到垂向和横向参数的优化取值,如表1、表2所示。
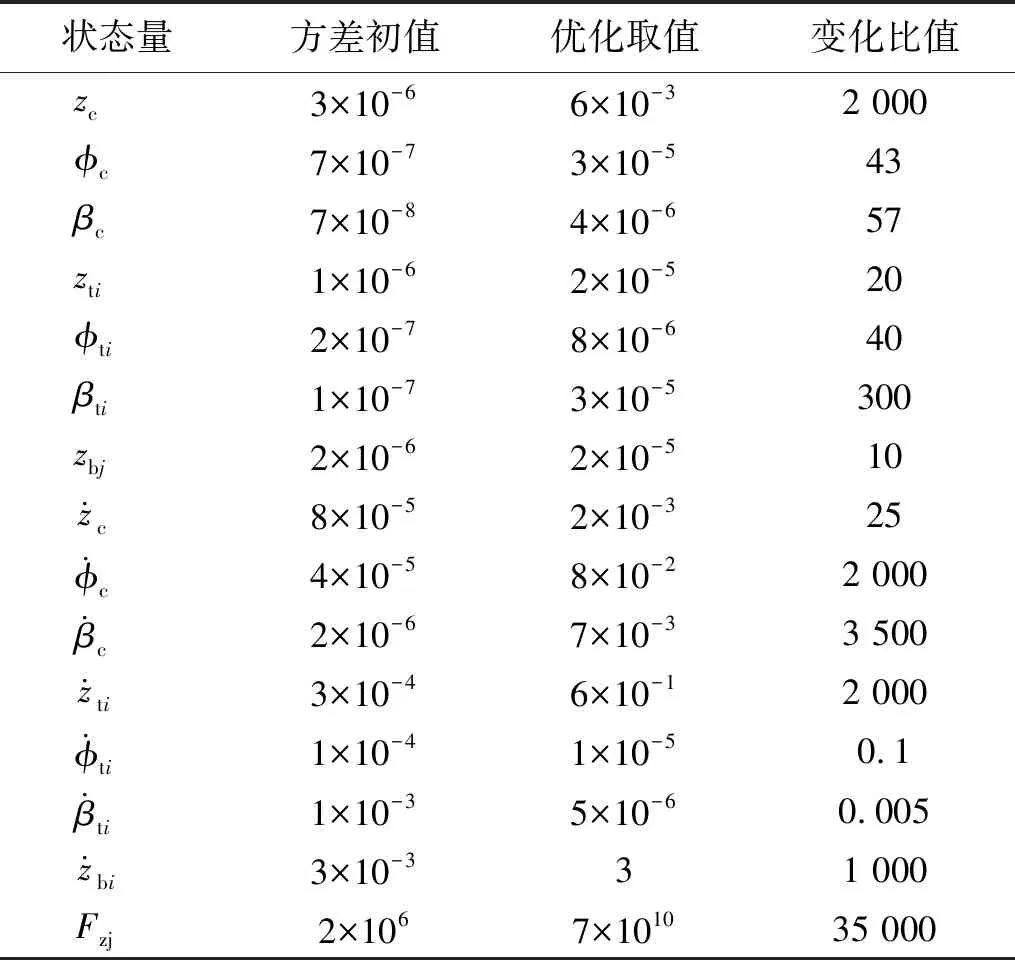
表1 垂向状态量参数取值

表2 横向状态量参数取值
表1和表2中的“变化比值”等于“优化取值”除以“方差初值”,用于比较参数在优化前后的变化情况。由表1和表2可知,垂向和横向各元素优化后的参数取值变化大小不同,有增有减,规律不定,优化效果还需通过仿真验证,进行对比分析。
3 仿真验证及结果分析
3.1 垂向反演结果
为反映关键滤波参数优化后的效果,将优化前后的参数值分别带入滤波系统中,得到图4的垂向反演结果对比图。图4(a)为1位轴箱轴承垂向力仿真值与优化前的时域特征对比图,图4(b)为优化后的垂向力时域特征对比图,将两图中间部分第9.0~9.5 s放大,观察反演趋势和波形,图4(c)为1位轴承仿真值、优化前、优化后垂向力的频谱特征对比图。表3给出了8个轴承优化前后的相关系数和决定系数,以及两者的百分比变化,其中

表3 垂向相关系数和决定系数及百分比变化
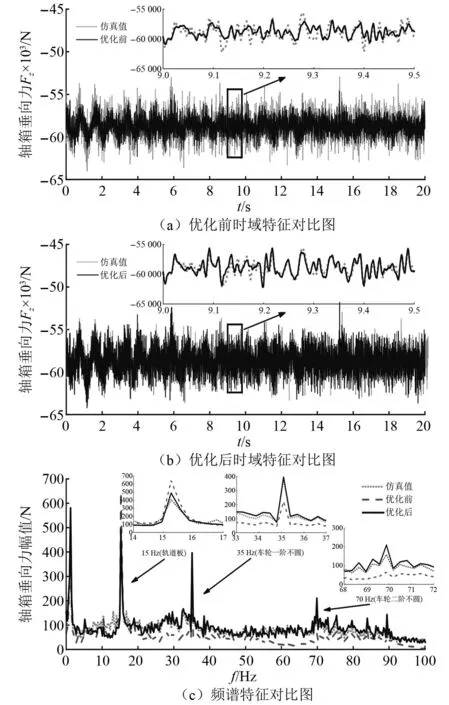
图4 参数优化前后垂向反演结果对比图
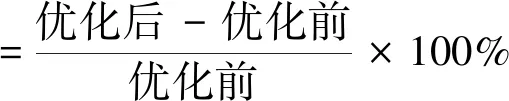
由图4可知,对过程噪声矩阵优化可明显提升卡尔曼滤波反演效果。从图4(a)与表3优化前的决定系数可看出,反演的时域幅值与仿真值有一定差异,曲线拟合效果较差,仅为0.5左右。从图4(a)的局部放大图和表3优化前的相关系数可看出,时域的变化趋势和相位不能准确吻合,波峰与波谷存在较大偏差,相关性系数仅为0.7左右。而从图4(b)中可看出,无论是时域的幅值还是变化趋势,都更加接近仿真值,曲线重合度较大,拟合效果好,说明参数优化起到作用。
由图4(c)可知,在频率为20~100 Hz中,优化前的峰值和波形与仿真值相差较大,而优化后的则能与仿真值基本保持一致,尤其在15 Hz处的轨道板激励频率,35 Hz及70 Hz处的车轮一阶和二阶不圆频率,都能较为准确地凸显出来。频谱特征对比图也进一步说明了:提高载荷估计的准确性需要对滤波参数进行优化。
整体分析表3,未优化的8个轴承反演结果欠佳,且存在部分恶劣情况,如第6位、第7位轴承,效果参差不齐。而参数优化后的反演结果提升明显,8个轴承的反演结果更加均衡,缩小了最大值与最小值之间的极差。相关系数最大提高了55%,整体达到了0.85~0.92,属于极强相关;决定系数最大提高了一倍多,整体在0.71~0.84之间,极大提高了反演值与仿真值的拟合效果。可见,对滤波关键参数进行优化,在大幅提高反演精度的同时,还能保证各轴承结果均衡。
3.2 横向反演结果
同样将优化前后参数分别带入卡尔曼滤波系统中,得到横向反演结果,如图5和表4所示。

表4 横向相关系数和决定系数及百分比变化

图5 参数优化前后横向反演结果对比图
由图5和表4可知,参数优化后可提升反演效果,其时域和频谱特征与仿真值基本一致。考虑到高速列车横向强非线性的特点,横向的相关系数在0.74~0.85,略小于垂向,但较优化前也有大幅提升,仍属于强相关。由于轴箱轴承横向力比垂向力更小,低频多,横向的决定系数在0.53~0.71,从幅值差异与拟合效果来看略差于垂向,但较优化前也有大幅提升。
整体来说横向规律与垂向相似,参数优化方法不仅能提高反演精度,还能保证各轴承结果均衡,两者的反演结果也验证了卡尔曼滤波轴承载荷反演模型的正确性,以及自适应小生境遗传算法对滤波参数优化方法的可行性,为高速列车轴箱轴承载荷及关键参数优化提供方法和经验。
综上,通过分析表1、表2,结合优化前后的反演结果可知:要想得到较好的卡尔曼滤波反演效果,过程噪声矩阵的参数并不是严格按照方差或协方差选取的,而是根据整个系统适当调整,且调整的多少,要根据反馈结果决定。除此之外,Q中各元素的大小还会随着车速、轨道谱激励等条件的变化而变化。若在多参数下根据每次反馈结果逐一手动调整,不仅工作量大,还很难保证反演质量,由于调整的方向和大小未知,也无法满足实时性。而利用自适应小生境遗传算法对关键滤波参数进行优化,可弥补以上不足,它以概率化的寻优方法自动调整搜索方向求得最优解,利用计算机的并行计算,根据不同需求和目标寻优求解,做到准确、快捷、通用性强。
4 结 论
通过对比高速列车轴箱轴承载荷的反演效果,分析参数,可得到以下结论:
(1) 本文通过建立高速列车轴箱轴承载荷反演模型,提出并验证了基于卡尔曼滤波算法的轴承载荷反演方法,利用自适应小生境遗传算法对关键参数优化匹配,提高了反演精度,实现了高速列车轴箱轴承边界载荷较为准确的估计。
(2) 过程噪声矩阵Q中的参数仅按数学方法取方差或协方差反演效果欠佳,存在部分恶劣情况,不能满足实际需求,说明了参数调整的必要性。参数经过优化后,大幅提升了反演效果,指标显示:参数优化后的反演结果更加均衡,且精度更高,时域和频域在幅值和变化趋势上基本与仿真值一致。从而验证了轴承载荷反演模型和自适应小生境遗传算法参数优化方法的正确性,为高速列车轴箱轴承载荷及关键参数优化提供方法和经验。
(3) 结合数据和对比结果反映出:要想得到较好的卡尔曼滤波反演效果,滤波关键参数的选取需要根据整个系统及反馈结果适当调整。自适应小生境遗传算法将代理模型与反演模型结合,实现了结果的在线估计和参数的在线优化,准确高效地匹配出最优参数。
本文对关键参数优化的方法,可以弥补手动调整参数的诸多不足,更能满足实际需求。此外,还可推广至铁道车辆轮轨力、悬挂力等部件的反演,或在其他卡尔曼滤波反演的参数确定及优化中应用,这将大幅提高可靠度,做到快速、准确、通用性强。

