一种基于贝叶斯的广义Pareto 分布变点估计
王国琴,吴有富,许 婷,欧永玲
(1.贵州民族大学数据科学与信息工程学院,贵州 贵阳 550025;2.贵州交通职业技术学院,贵州 贵阳 550025)
在统计学中一个比较热门的研究问题就是变点问题,它被用于经济学、气象学、医学等领域。研究变点的方法主要有最小二乘法、极大似然法、贝叶斯方法、非参数方法等。随着人们不断地研究,在技术方面得到快速发展,贝叶斯方法在变点问题分析中应用越来越广泛。
广义Pareto 分布是由Pickands[1]首次提出,在许多领域得到广泛应用。近年来许多学者对广义Pareto分布进行研究分析。刘媚和汤银才[2]在完整数据下研究混合广义Pareto 分布的参数估计;刘金霞和韩立岩[3]利用广义Pareto 分布对现金流风险价值进行分析;陈海清和程维虎[4]利用最小二乘法得到两参数和三参数广义Pareto的参数估计;张月等[5]在加权平方损失函数下,利用经验Bayes 估计对广义Pareto分布的形状参数进行估计,及估计的收敛速度;马志迁[6]利用多种参数估计方法对广义Pareto 模型的参数进行估计,并比较其方法的优劣;张中献[7]基于最小二乘概念,对广义Pareto 分布的参数估计进行更深入的研究。
目前针对广义Pareto 分布变点研究情况如下,Chen 等[8]将广义Pareto 分布应用到极端事件变点问题分析;Renard等[9]分布考虑了平稳、跳跃、线性趋势变化下三种情况广义Pareto 分布变点特征;Dierckx等[10]利用Pareto与指数分布的关系,对Pareto分布于广义Pareto 分布变点检测方法进行比较;Susan 等[11]研究广义Pareto 分布形状参数变点检测,基于Kullback-Leibler 散度的似然比统计量对变点检测,用极大似然方法来估计。通过检索我们发现,关于对广义Pareto 分布变点研究很少。经过实验对比我们发现Susan方法的估计精度并不高,在小样本下估计效果可行,但发现大小样本效果均不如我们的。
1 广义Pareto 分布单变点模型
文章主要研究广义Pareto 分布,其分布函数为;
假设随机变量yi相反独立且满足
变点研究常用方法有极大似然法、贝叶斯方法、非参数方法等,使用不同的方法会有不同的估计效果。文章主要利用贝叶斯方法对广义Pareto 分布进行变点估计,为了验证贝叶斯方法的有效性,利用极大似然与贝叶斯方法做比较。因此接下来分别用极大似然法与贝叶斯方法对参数进行估计。
2 贝叶斯估计
利用贝叶斯处理变点问题时,会通过引入先验分布,根据先验分布和样本分布来确定后验分布,但在这方面的知识不完全,通常学者会选择无信息先验分布。文章选用无信息Jeffreys 分布作为先验分布,在此基础上讨论MCMC 算法估计广义Pareto 分布的变点位置,记m 为变点,且,似然函数为
其中
则有
(1)对变点位置m 取无信息先验分布取2 到n-1上的均匀分布
其中样本似然函数为
则由贝叶斯公式求得的联合后验分布为
可得各参数的满条件分布为
3 数值仿真及比较
(1)极大似然与贝叶斯方法比较
广义Pareto 分布单变点模型为
基于上述贝叶斯估计的讨论,下面利用R 软件对其进行数据模拟实验分析。
表1 参数的极大似然估计与贝叶斯估计
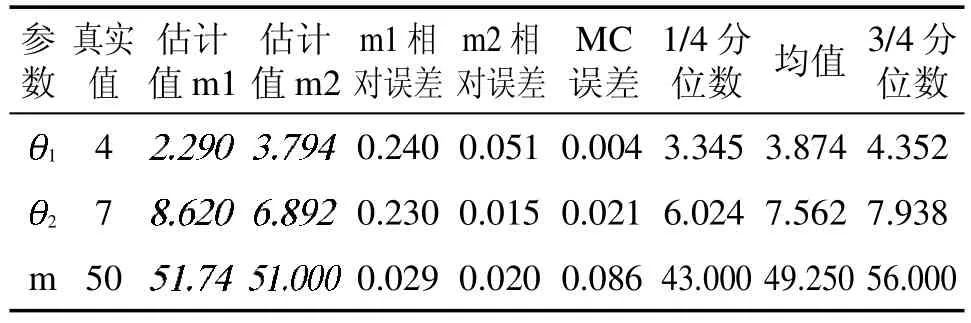
表1 参数的极大似然估计与贝叶斯估计
参数真实值估计值m1估计值m2 m1 相对误差m2 相对误差MC误差1/4 分位数 均值3/4 分位数1 4 0.240 0.051 0.004 3.345 3.874 4.352 2 7images/BZ_114_1428_2320_1449_2346.pngimages/BZ_114_1455_2320_1476_2346.pngimages/BZ_114_1474_2320_1495_2347.pngimages/BZ_114_1577_2320_1598_2347.png0.230 0.015 0.021 6.024 7.562 7.938 m 50images/BZ_114_1456_2386_1494_2412.pngimages/BZ_114_1531_2386_1553_2412.pngimages/BZ_114_1577_2386_1615_2412.pngimages/BZ_114_1429_2452_1450_2478.png0.029 0.020 0.086 43.000 49.250 56.000
从图1,图2,图3 知,在抽样过程中波动较小,绝大多数都是在参数位置波动,则估计效果较好。图4是两条迭代链,两条链的初始值分别为(4,7,50),(2,4,50),从图可以看出,两条链几乎重合,即收敛性较好。接下来给出三个参数的后验分布的核密度估计图。

图1 参数1 的迭代图
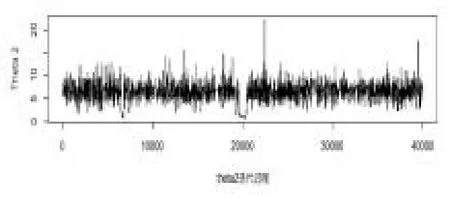
图2 参数2 的迭代图

图3 参数m 的迭代图

图4 参数m 的两条迭代图
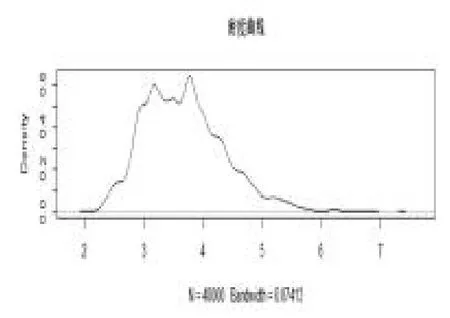
图5 1 后验分布的核密度估计图
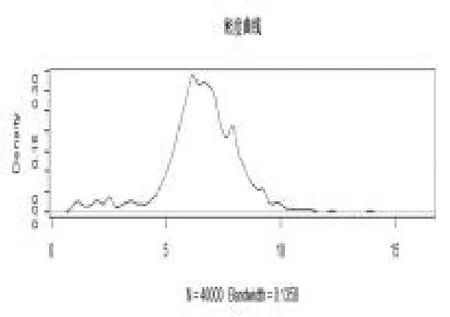
图6 2 后验分布的核密度估计图
图7 m 后验分布的核密度估计图
表2 不同样本量下参数的贝叶斯估计

表2 不同样本量下参数的贝叶斯估计
总样本量 100 200 500 1000 1500 2000 1 样本量 50 120 200 400 800 1300 2 样本量 50 80 300 600 700 700 1 估计值 3.794 3.398 4.371 3.921 4.278 4.064 2 估计值 6.892 6.5952 7.148 6.865 6.613 6.906 m 估计值 48 118 202 559 800 1287
从表2 知,在总样本量n=100,200,500,1000,1500,2000 时,三个参数的估计值都非常接近,,m=50。不管样本量增加多少,估计值都比较接近真实值。
(2)本文方法与Susan 方法比较
将贝叶斯方法与Susan[11]方法做对比,结果如表3 所示,表中m 为变点位置,m1 为利用贝叶斯方法得到的估计值,m2 是基于KL 散度的似然比统计量的极大似然方法得到的估计值。
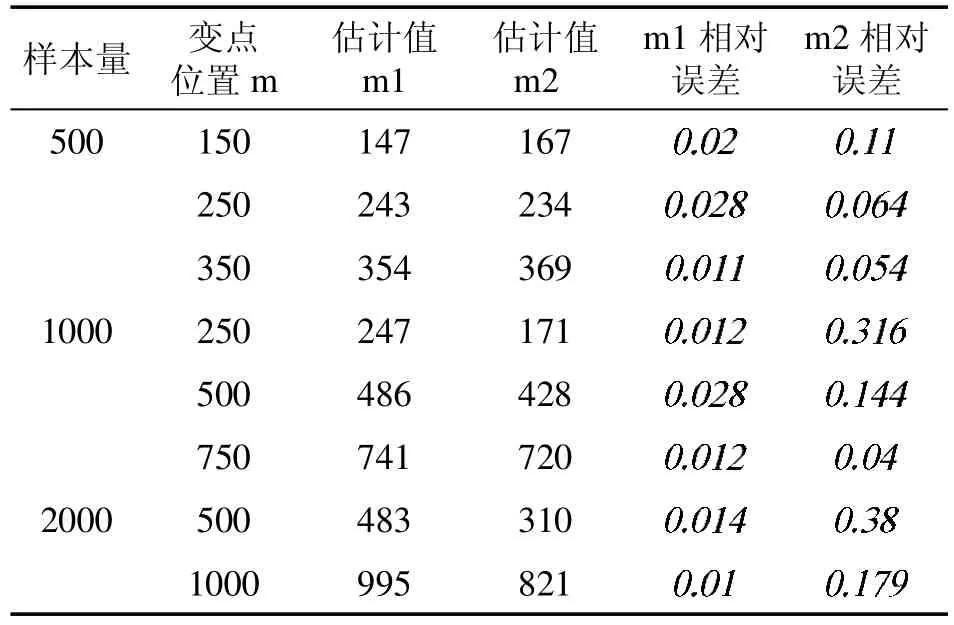
表3 利用贝叶斯与Susan 方法对变点位置进行估计
从表3 知,变点位置m=250 时,当样本量从500增加到1000 时,贝叶斯变点位置相对误差从0.028变化到0.012,而Susan[11]方法的变点位置相对误差从0.064 变化到0.316;变点位置m=500 时,当样本量从1000 增加到2000 时,贝叶斯变点位置相对误差从0.028 变化到0.014,而Susan[11]的变点位置相对误差从0.144 变化到0.38。由此可知,当变点位置不变,随着样本量的增加,贝叶斯估计优于Susan[11]方法。并且在相同样本量下贝叶斯估计相对误差均小于Susan[11]的相对误差。因此贝叶斯估计不仅在大样本下优于Susan[11]的方法,而且在小样本上贝叶斯方法更好。
4 结论
文章主要研究广义Pareto 分布单变点问题,利用贝叶斯方法对其进行分析,并与极大似然方法和Susan[11]的方法进行比较。根据表1 结果,极大似然方法与贝叶斯方法都能估计出参数值,在对相对误差下比较,贝叶斯方法优于极大似然方法。根据表2 结果,随着样本量的增大,三个参数的估计值都比较接近真实值。根据表3 结果,在大小样本下,贝叶斯估计方法均优于Susan[11]的方法。以此得出利用贝叶斯方法估计变点位置会更好且有效。

