基于深度强化学习的多无人车系统编队控制1)

曾毓凌 郝宇清 于 颖 王青云

(北京航空航天大学航空科学与工程学院,北京 100191)

引言

21 世纪以来,随着半导体技术、车辆技术、控制科学、人工智能和通信技术的不断发展,无人机和无人车等新颖的运载设备逐渐从最初的创意设计变成了我们日常生活中的一部分.随着工业发展中不断升级的制造需求和对更先进的生产力需求,无人车和无人机等工具也从一个传统的运载体向智能体的方向发展,其智能化程度正在飞快发展.然而,由于现代工程的复杂性和多样性,许多任务很难通过单个智能体完成,如大型设备的搬运和组装、大规模搜索与识别、复杂矿洞的数字建模,以及多样性的军事作战任务等.在许多这样的场景中,多智能体的协作往往能比进行单一智能体的功能扩充带来更好的效果,例如节省复杂系统的研发成本,减少对硬件和软件复杂性的要求[1].一个典型的例子就是在空战中不同种类飞机的配合,其协同作战效率和能力远大于将所有功能集成于单一飞机[2].

关于多智能体协同控制问题,目前主要的研究方向有一致性控制[3-4]、编队控制[5]和编队-合围控制[6]等.多智能体协同控制的控制器设计方法目前主要有领导-跟随法[7-8]、虚拟结构法[9]、基于行为法[10]及基于一致性理论的方法[11-12]等.但现有的控制器设计方法大多是基于精确的线性模型,不能很好地刻画地面轮式车辆等运载体的动力学行为.无人车的动力学行为具有较强的非线性,且存在非完整约束和欠驱动问题,传统的基于线性系统理论设计的控制器有时候在实际无人车控制中效果欠佳.况且,当模型具有不确定性时基于精确模型的控制方法鲁棒性较差.而机器学习的方法具有强大的拟合能力,对模型的要求度低,已广泛应用在各种力学问题当中[13].相较于基于精确模型设计控制器的方法,强化学习的基本思路不再是人为地利用多智能体的精确模型设计各种形式的控制器,而是利用机器学习的方法建立高维状态空间到动作空间的映射,相当于一个黑箱控制器模型,是一种较为新颖的控制器设计方式[14].结合了深度神经网络的深度强化学习在特征表示方面具有非常强大的能力,该能力在构建状态-动作映射时发挥了重要作用,在非线性动力学与控制问题以及欠驱动控制问题中具有较好的应用价值[15].况且,模型的训练只需要智能体的输入输出数据,而不需要系统的精确模型,本质上是一种数据驱动的无模型控制方法,在模型参数未知、模型存在扰动和摄动时仍然可以学习到控制器[16].传统的基于模型的控制方法与基于深度强化学习的控制方法的优缺点对比如表1 所示.

表1 两种控制方法对比Table 1 Comparison of two control methods

Bae 等[17]结合CNN 卷积神经网络和强化学习算法解决了多机器人的路径规划问题.Zhu 等[18]利用MADDPG 算法解决多机器人运动避障问题,并加入了优先经验回放机制来更好地利用强化学习随机动作储存的经验数据,但其使用的是质点运动学模型,并不能很好地刻画真实的多智能体运动.Hung等[19]利用Q-learning 的强化学习算法,结合无人机运动学模型,解决了领导-跟随问题.李波等[20]利用MADDPG 算法解决无人机群在威胁区域中的“避险”飞行问题.张海峰等[21]针对非线性多智能体控制问题,利用HJB 方程来设计控制律,并利用强化学习的方法来求解HJB 方程进而得到最优控制器.赵启等[22]利用D3QN 深度强化学习算法和无人机运动学模型来研究长机-僚机编队的横向距离保持问题,后续又采用DDQN 深度强化学习算法研究长机-僚机编队中的横向距离保持和纵向速度跟踪问题[23].马晓帆[24]主要研究了商用车队的编队道路运行问题,构建了六自由度商用车动力学模型,利用TD3 算法来实现车队的纵向编队运行.相晓嘉等[25]提出了ID3QN 算法来研究固定翼无人机的定高长机-僚机编队问题,ID3QN 算法是在D3QN 的基础上增加“模仿”行为,旨在帮助僚机更快速地取得跟踪长机效果较好的经验数据.以上文献主要基于运动学模型进行控制器设计,但实际的动力学系统往往是二阶系统,由于惯性的存在,速度控制必然存在一定时延,力控制是最直接而准确的控制方式,在实际工程问题中具有更好的应用价值.

本文旨在利用深度强化学习技术设计多无人车系统的编队控制器,使多无人车系统形成指定的期望队形,并对控制器进行策略优化.本文的创新点包括以下三个方面.第一,基于DDQN 深度强化学习算法,结合一致性理论和伴随位形的思想设计多无人车系统的编队控制器,该控制器在无精确模型只有运动数据时也可以实现编队控制任务,降低了对模型的依赖性,相比传统的基于模型设计的控制器,本文给出的控制器鲁棒性更强;第二,相较于目前大多数文献基于运动学模型设计控制器,本文直接基于动力学模型设计力控制器,更具有实际意义;第三,本文创新性地提出了编队起始阶段的等候与启动条件,进行了策略优化,仿真显示优化后的策略有效节省了编队所需的能量.

1 无人车动力学模型

常见的车辆动力学模型有阿克曼转向模型[24]、麦克纳姆轮转向模型[26]和后轮差动转向[27]等.后轮差动转向的车辆硬件与结构更加简单,常用于小型轮式机器人等.本文拟采用后轮差动转向的刚体无人车动力学模型.

考虑后轮差动转向的无人车模型,其左右两侧后轮由两个电机独立驱动,两侧的前轮仅用于支撑车辆和配合运动,不产生控制作用[28].无人车相对惯性坐标系定义的位形坐标为 η=(x,y,θ)T,代表了无人车的质心位置以及车头朝向,无人车的几何模型如图1 所示,各参数如表2 所示.

图1 无人车几何模型Fig.1 Unmanned vehicle geometric model

表2 无人车几何参数Table 2 Unmanned vehicle geometric parameter

无人车的动力学方程为[29]

需要注意的是,该无人车动力学模型仅仅用于运动的仿真和运动数据的获取,在控制器的设计与训练中并不需要该动力学模型.

2 基于DDQN 的多无人车编队控制

2.1 问题描述

考虑含有N+1 个无人车的多无人车系统,其中包含1 个领导者无人车和N个跟随者无人车,其状态由位形坐标与速度变量表示.无人车的位形坐标记作xi=(xi,yi,θi),i=1,2,···,N;其速度变量记作vi=(vi,ωi),i=1,2,···,N.其中第0 号无人车为领导者,第1 至N号无人车为跟随者.

编队控制问题的控制目标是使得多无人车系统形成期望的队形,如下式所示

2.2 问题分析

为了实现多无人车系统的编队控制,可以先从单领导者单跟随者问题出发,再利用树状通讯扩展到多无人车系统的编队控制问题.首先考虑单个跟随者和领导者的编队控制,领导者状态表示为xl=(xl,yl,θl) 和vl=(vl,ωl),跟随者的状态表示为xf=(xf,yf,θf)和vf=(vf,ωf) .任务目标为设计合适的控制器,使得跟随者的状态与跟随者的状态之差等于期望的相对位形d,即

观察上式,可以构造领导者的伴随位形 (xl-d),称之为伴随领导者.若跟随者实现对伴随领导者的一致性跟踪,则等价于实现了对领导者的编队控制.因此,可利用构造伴随领导者的方法将编队控制问题转化为一致性问题.伴随领导者的几何示意图如图2 所示.

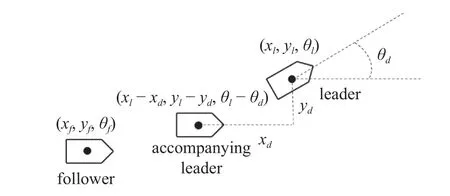
图2 伴随领导者Fig.2 Accompanying leader

2.3 DDQN 深度强化学习算法

强化学习技术作为机器学习的一个分支,凭借其在解决复杂的序列决策问题中的优异表现,在控制工程领域和多智能体协同领域得到了广泛的应用[1].其基本思想是在无经验的情况下通过智能体与环境的交互,获取反馈并积累经验,然后优化智能体的决策模型,其基本思想如图3 所示.

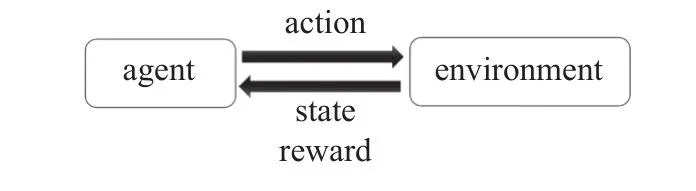
图3 强化学习基本思想Fig.3 Reinforcement learning basic idea

DDQN 算法是一种经典的深度强化学习算法,全称为double deepQnetwork learning,旨在利用深度学习的思想构建深度神经网络来建立从智能体状态st到价值函数Q(st,at) 的映射,其中st代表当前时刻的状态,at代表智能体做出的动作,rt代表智能体在本次交互中获得的奖励[30].该算法的特点是构建了价值网络与目标网络两个神经网络,在训练时可以有效避免因自举现象产生的价值函数高估问题,具有较好的稳定性,且其原理和架构的复杂程度不高,对硬件的要求低,便于无人车系统部署.

强化学习的最终目标是学习到最优策略π*(a|s),使得期望折扣奖励R最大,期望折扣奖励定义为

其中,γ 为折扣因子,代表未来的奖励折算到当前时刻的比例,rt为即时奖励,T为终止时刻.奖励函数r(s,a)通常根据具体任务来进行设计,便于针对性地进行优化,例如在多无人车一致性控制任务中加入位形误差、速度误差等变量.

准确的价值函数Q*(s,a) 代表的是神经网络在状态s下执行动作a所能获得的期望折扣奖励的期望值,其表达式为[13]

在学习到了准确的价值函数后,便可以在不同状态下评估最优动作并进行控制.

2.4 控制器状态与动作空间设计

为了实现利用DDQN 算法建立控制器实现控制目标的任务,需要设计合适的状态空间和动作空间,在经过多轮测试后,选取局部坐标相比于惯性系下的全局坐标能使网络学习到更准确的特征,控制效果会有明显的进步,由于是设计跟随者的控制器,故设计状态空间时需要将领导者与跟随者的全局坐标转化为在跟随者坐标系下建立的相对坐标,几何示意图如图4 所示.

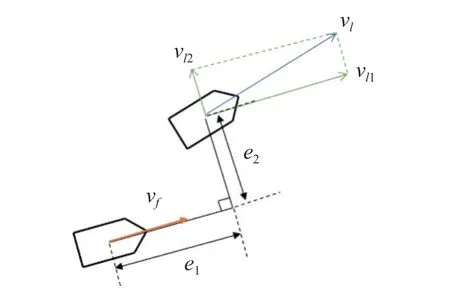
图4 状态空间Fig.4 State space

状态空间定义为

其中,e1和e2为跟随者坐标系下的纵向距离误差和横向距离误差,vf为跟随者的运动速度,vl1和vl2为领导者的运动速度在跟随者坐标系下的纵向和横向分量,ωf和ωl为跟随者和领导者的角速度.各个局部坐标变量与惯性坐标系下的变量转换关系为

考虑到DDQN 算法输出神经元数量有限,需要将动作空间进行离散化,才能使输出层的各个神经元输出价值函数Q(s,a)[31].本文基于无人车系统动力学模型来设计控制器,控制输入为左右侧后轮的转矩,需要对驱动力矩进行控制来改变运动状态.其转矩的和值控制无人车纵向的加减速,其转矩的差值控制无人车沿竖直方向的角加速度.考虑到纵向加减速可分为加速、减速和保持速度3 个动作,转动增大角速度、减小角速度和保持角速度3 个动作,两个维度耦合后可以得到9 种动作,因此取动作空间为9 种典型动作构成的集合.

2.5 控制器训练环境

为了使网络学习到符合实际物理意义的价值函数Q(s,a),需要针对控制目标设计对应的奖励函数,显然一致性控制问题下,位形误差与速度误差越小,系统的状态越佳,因此设计奖励函数为

其中,相对距离与相对速度的计算方法如下

该奖励函数的具体含义是: 相对距离越小,状态越接近一致,具有更高的价值,所以奖励与相对距离呈负相关,不同区间的不同梯度有助于模型在误差较小时提高敏感性,避免在误差较小的区间内因为奖励函数的值变化较小而学习效果不佳.在本任务中,取ed=0.01 m 为收敛阈值,认为距离误差小于该阈值时实现了一致性跟踪,故距离奖励的最大值定义在ed＜0.01 m 的情况.将相对速度引入较小的负奖励可以使模型的过渡阶段尽量平滑,避免出现过大的速度差值.

基于以上的状态与动作空间、奖励函数以及无人车刚体动力学模型,便可以构建基于DDQN 算法的一致性控制器训练环境和运动仿真环境,如图5 所示.

图5 控制训练环境Fig.5 Controller training environment

在每一个控制周期内,无人车将状态变量输入神经网络并得到价值函数输出,然后利用动作选择策略来决定跟随者的控制量,训练时常采用带有一定随机性的动作选择策略来使得网络探索更多的动作.动作选择完成后,环境将更新领导者与跟随者的下一状态,并计算该次控制得到的奖励函数,然后将经验数据即环境交互得到的四元组(st,at,rt,st+1)存入经验记忆库,再从经验库中采样并更新网络.

为了在网络训练时模拟到更全面更复杂的环境来指导神经网络的更新,避免网络陷入局部最优,在设计训练场景时需要充分增加随机性,避免因为轨迹和场景的单一导致网络过拟合,泛化性差.因此考虑如图6 所示的4 种典型运动,分别为匀速直线运动、加减速、左转和右转.

图6 4 种典型运动轨迹Fig.6 Four typical trajectories

在每一轮训练开始前,环境会生成 40 s 的领导者运动轨迹,其中每 4 s 为一段.每一轮训练共由10 段轨迹拼接而成,每一段轨迹都为上述4 种典型轨迹之一,且为均匀抽样,以实现训练过程的领导者轨迹多样性.

在训练中,领导者无人车的起始位形和速度为(xl0,yl0,θl0,vl0,ωl0)=(0,0,0,0.2,0).跟随者的起始位置在以领导者起始位置为中心,以 6 m 为边长的正方形内随机生成,起始姿态角,按照均匀分布随机选取.

神经网络的结构及参数如图7 和表3 所示.

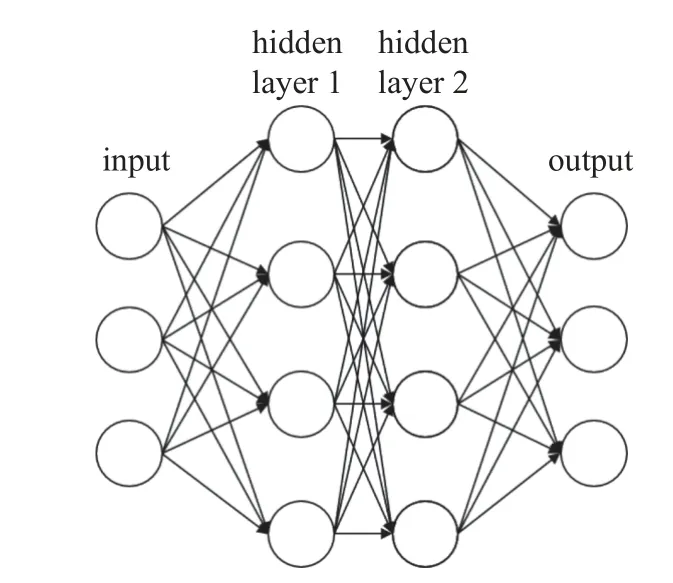
图7 神经网络结构Fig.7 Neural network framework

表3 神经网络参数Table 3 Neural network parameters

2.6 控制器训练结果

基于以上的训练环境,设置网络训练的总轮次为10 000 轮,初始学习率为0.000 1,记忆库总容量D为 218,每次更新网络的采样数量为256,折扣因子γ为0.95,训练结果如图8 所示.

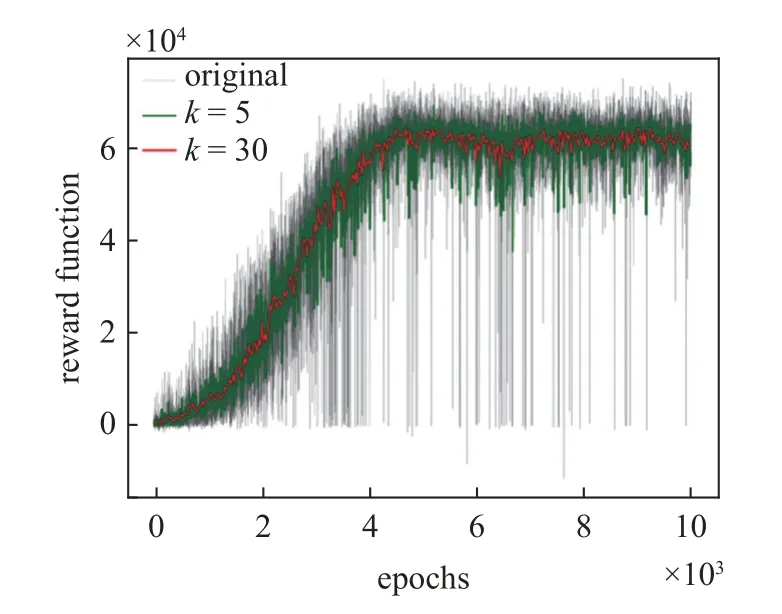
图8 训练结果Fig.8 Training result

可以看到,随着网络的训练,每轮次所获得的奖励函数和值在不断增大,网络训练后期奖励函数和值趋于收敛.由于网络训练时模型决策因为有较小的探索率会存在动作的随机选择,并且每个轮次的领导者轨迹与起始位置不同,因此会造成奖励函数和值的波动,可用滑动窗口平均值观察网络的收敛性,图中取窗口大小k=5和k=30 两组参数进行绘图,可以观察到网络在训练后期收敛于较高的奖励值,模型趋于收敛.然后,将动作选择策略的随机性消除,按照价值最大策略进行控制,对模型进行验证,控制器结构图如图9 所示.

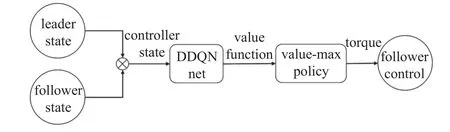
图9 控制器结构Fig.9 Controller framework

进行100 轮验证,结果如图10 所示.

图10 验证结果Fig.10 Test result

同样使用滑动窗口平均法观察验证过程的奖励函数,可以观察到模型的表现较为稳定,曲线有所波动的原因与领导者轨迹的随机性和初始位置的随机性有关.经验证,该网络可以在训练场景下实现跟随者状态对领导者状态的跟踪.

3 仿真验证

3.1 运动仿真结果

考虑由5 台无人车组成的多无人车系统,通讯方式为树状拓扑,如图11 所示.其中,0 号无人车为领导者,其他为跟随者,其中1 号和3 号无人车都与领导者进行通讯,可以获取领导者的运动状态,但2 号和4 号无人车只能分别与1 号和3 号无人车进行通讯,获取对应无人车的状态,而不能得到领导者的运动状态,以模拟分布式通讯的场景.领导者按照期望轨迹进行运动,跟随者在控制器的控制下运动.

图11 通讯拓扑Fig.11 Communication topology

各无人车的物理参数如表4 所示.

表4 无人车物理参数Table 4 Unmanned vehicle physical parameter

无人车的初始位形为

无人车的期望队形为五边形,具体的队形参数为

引入期望队形的信号后,便可将一致性控制器转化为编队控制器,控制器的结构图如图12 所示.

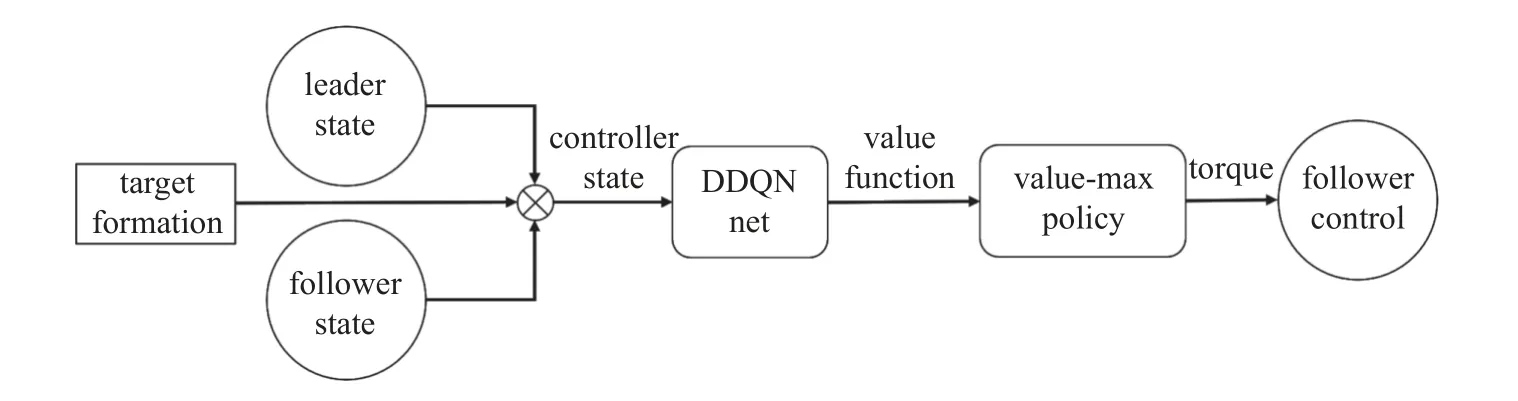
图12 编队控制器结构Fig.12 Formation controller framework

设置期望队形为五边形,领导者运动轨迹覆盖加减速、左右转等情况,所有跟随者初始时刻静止,进行运动仿真,结果如图13 和图14 所示.

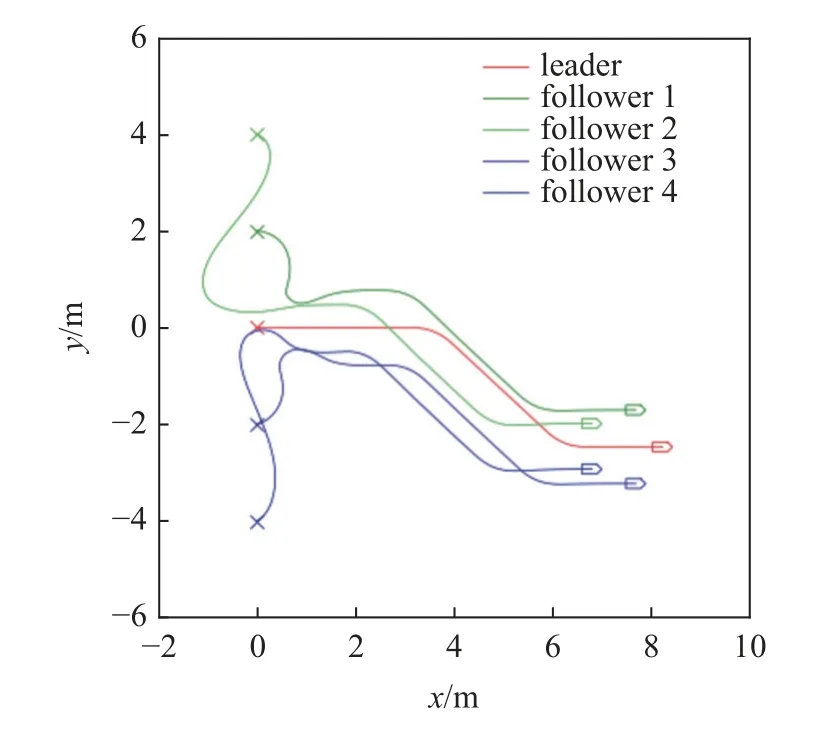
图13 无人车轨迹Fig.13 Unmanned vehicle trajectory

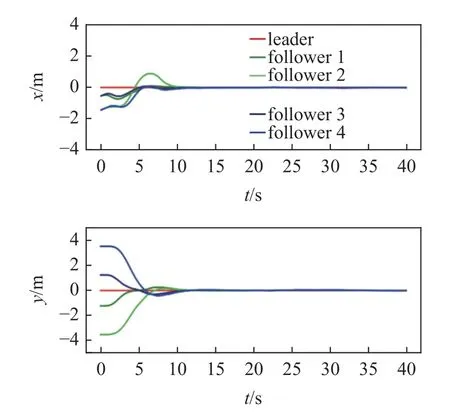
图14 编队误差曲线Fig.14 Formation error

根据运动轨迹和误差曲线可以观察到,多无人车系统在该控制器的控制下成功实现了期望的编队运动.

为了充分验证控制器的有效性,需要针对不同的期望队形开展运动仿真实验,图15 和图16 为不同期望队形的运动仿真结果,其中图15(a)和图16(a)为五边形队形,图15(b)和图16(b)为平行队形,图15(c)和图16(c)为合围四边形队形.领导者运动轨迹也包含了左右转、加减速等典型运动情况.通过运动轨迹和误差曲线可以看到,不同期望队形下,控制器均能驱动多无人车系统快速实现编队并保持队形稳定运动.

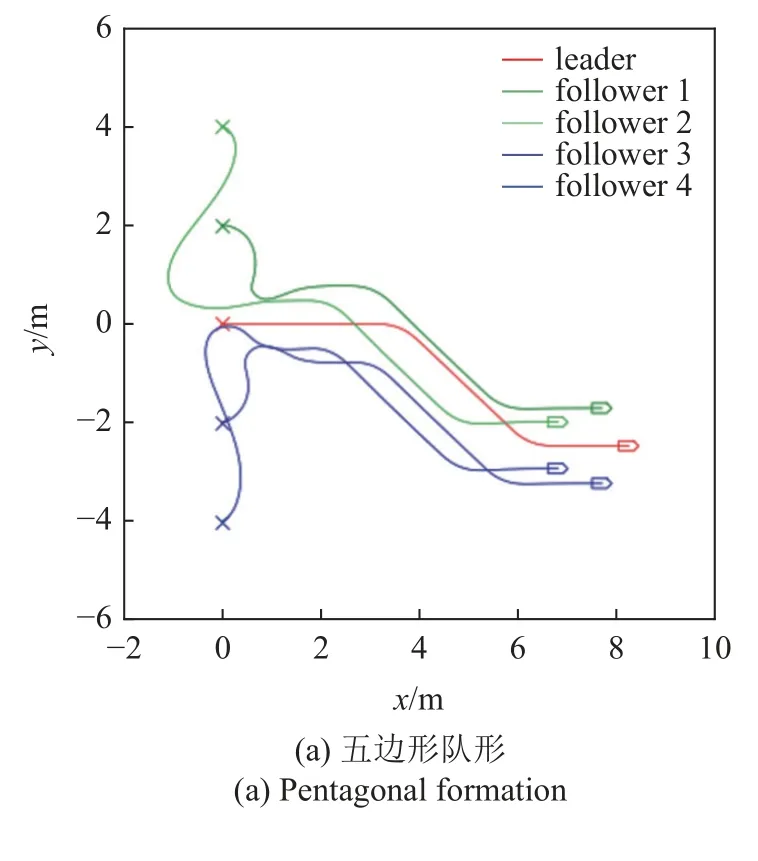
图15 多队形测试轨迹Fig.15 Multiple formation testing trajectory

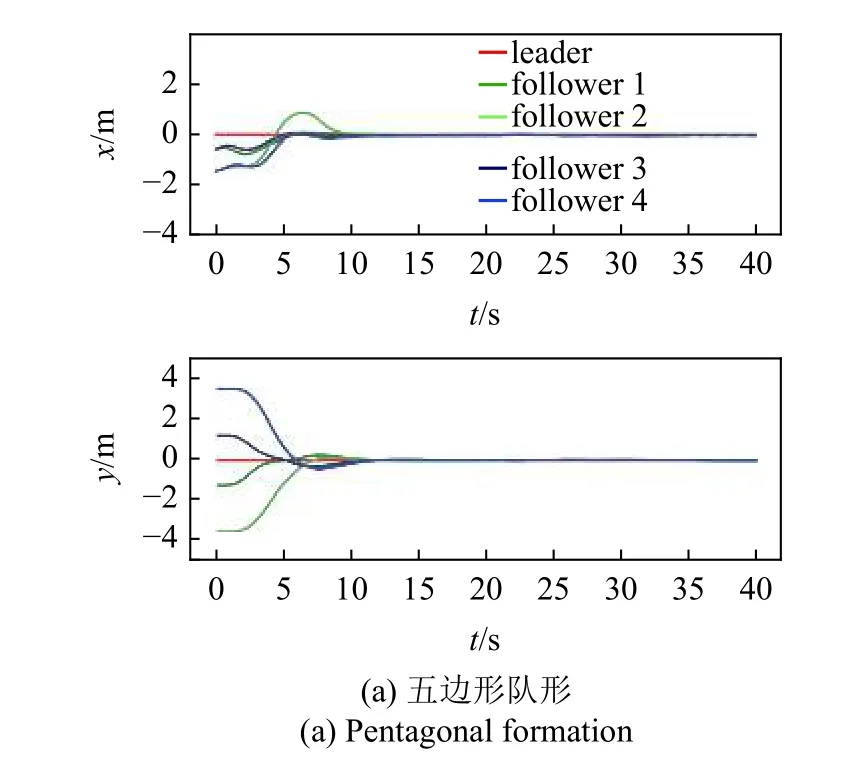
图16 多队形测试误差曲线Fig.16 Error plot of multiple formation testing

在现实场景中,往往由于地形等原因,多无人车编队需要在运动过程中进行队形切换,因此需要验证控制器在运动过程中变换队形的能力.图17 和图18 为队形切换的运动仿真结果,多无人车系统在运行过程中由于遇到障碍需要收紧队形,通过后恢复原队形.运动轨迹和误差曲线显示多无人车系统能够在控制器的驱动下,在运动过程中期望队形发生变化时快速转换为新目标队形,验证了在运动过程中的队形切换能力.

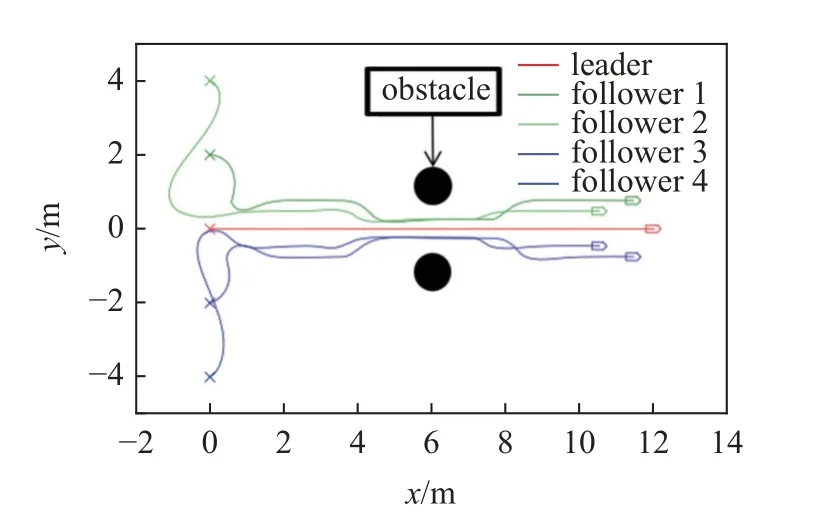
图17 队形切换测试轨迹Fig.17 Formation switching test trajectory

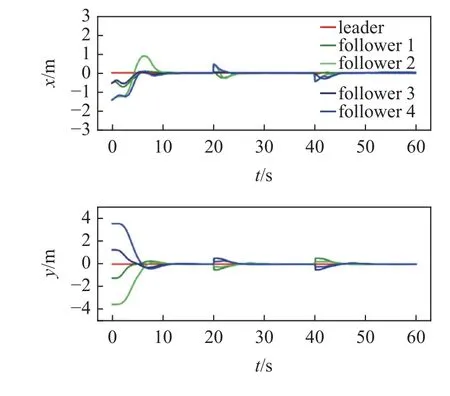
图18 队形切换测试误差曲线Fig.18 Formation switching test error plot

3.2 起始阶段策略优化

上文中的运动仿真证明了编队控制器的有效性,但通过对多无人车系统运动轨迹的观察可以发现,在编队控制的多队形实验中,当无人车起始位形为平行排布时,五边形编队任务中存在一定的反向运动现象,即运动过程中跟随者与领导者的速度方向夹角出现钝角,即vf·vl＜0,图19 为第4 s 时刻的无人车状态.

图19 反向运动时刻Fig.19 Reverse movement moment

造成该现象的原因是在起始位形下根据领导者计算各个跟随者的伴随领导者时,跟随者对伴随者的纵向跟踪误差为负,也就是两者之间的距离误差在跟随者的速度方向投影为负,导致跟随者需要向领导者速度方向的反方向运动才能对伴随领导者实现跟踪,故存在“反向运动”现象,由于需要进行更多的转向和加减速动作,该现象会增大控制过程中消耗的能量.

考虑单领导者-单跟随者的编队控制起始阶段状态.考虑 θf0=θl0且e1＜0,vl0≥0,vf0=0 的初始情况,如图20 所示.

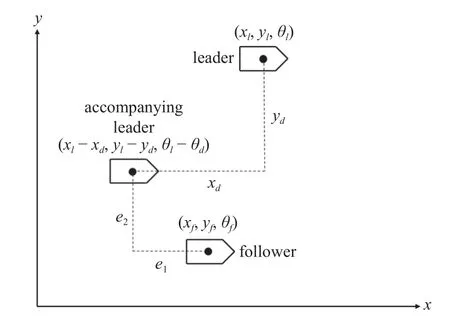
图20 反向运动典型状态Fig.20 Reverse movement typical condition

显然,该初始情况与上述五边形编队的所有跟随者的情况相同,是典型的易引起反向运动的起始条件.然而显而易见的是,该情况下若跟随者保持静止等候,在短时间内也会由于领导者的自身运动而使得编队误差减小,而不消耗任何能量,这是因为e1＜0,vl1-vf＞0,两者纵向的相对速度与位置误差异号,故纵向位置误差的大小将在一定时间内自行减小.由于考虑 θf0=θl0的初始情况,在起始时刻临近的短时间内横向误差e2基本不变,为简化模型暂不考虑横向的误差状态.

为了消除反向运动情况,现基于领导者与跟随者的纵向状态量定义单个无人车的等候条件与启动条件,等候条件为

其物理含义为,纵向距离误差与速度误差符号相反,具有自发消除误差的趋势,因此跟随者保持静止不动仍然能使得编队误差减小.

定义启动条件为

其物理含义为,纵向距离误差与速度误差符号相同,位置误差的绝对值将趋于增大,因此必须引入编队控制器的作用来驱动各个无人车达成期望队形.

各个无人车从初始时刻开始,在每个时间差分内都要进行等候条件与启动调节的判断,若满足等候条件则不进行控制,保持初始状态;若满足启动条件,则由DDQN 编队控制器持续进行控制.需要注意的是,由于以上分析都是基于 θf0=θl0的运动初始阶段,该动作策略仅用于运动初始阶段的能量优化,每个无人车一旦在某时刻达到启动条件,在后续时刻就不再进行条件判断,而是由编队控制器驱动无人车以实现控制目标.

3.3 对比分析

为了验证该策略的作用,采用五边形编队进行运动仿真以对比分析.运动仿真结果如图21 和图22所示.

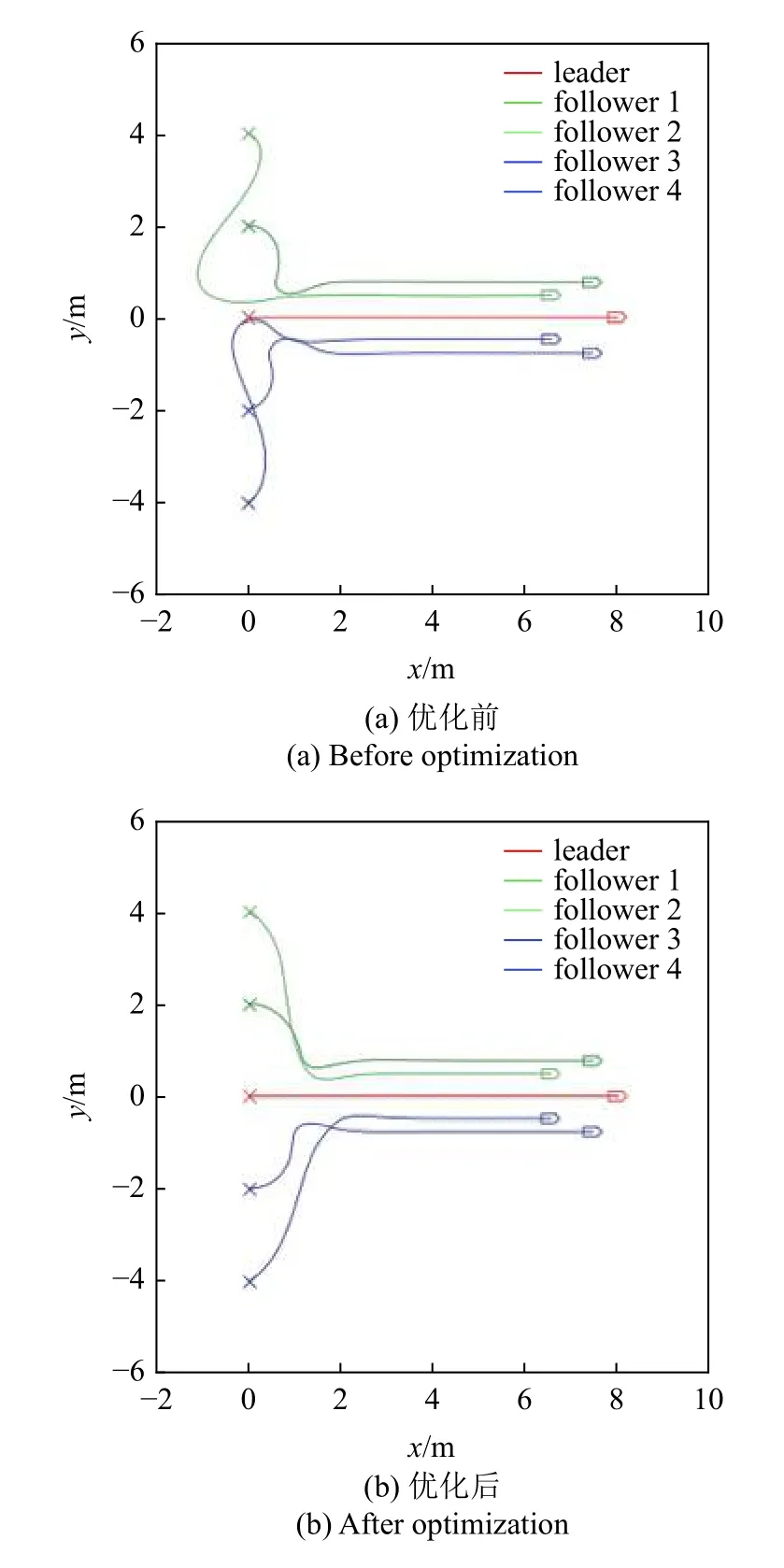
图21 运动轨迹对比图Fig.21 Trajectory comparison

图22 误差曲线对比图Fig.22 Error-curve comparison

其中,图21(a)和图22(a)分别为优化前的运动轨迹与误差曲线,图21(b)和图22(b)为优化后结果.经计算,加入该策略后,运动过程中所消耗的能量减少了19.93%,有效验证了该策略节约能量的作用,并且通过对运动轨迹的观察可以发现该策略消除了反向运动现象.但值得注意的是,由误差曲线的对比可知,能量优化伴随着收敛时间增大的代价,这是由于等候的过程实际上消耗了一定的时间.虽然该策略可以在节省一部分能量的情况下完成编队任务,但因为其设计原理而必然伴随着收敛时间延长.

4 总结

本文基于DDQN 深度强化学习算法,结合一致性理论与伴随领导者设计了多无人车系统的编队控制器.首先,进行了编队问题简化,将编队控制问题转化为对伴随领导者的一致性跟踪问题,然后简化为单领导者-单跟随者问题,并对该问题设计了基于跟随者局部坐标系的7 维状态空间、9 维动作空间和基于距离误差和速度误差的奖励函数.然后搭建了DDQN 网络的训练环境,设计神经网络架构参数后,引入初始位置和领导者训练轨迹的随机性进行网络训练.训练完成后利用运动仿真验证了控制器的有效性,并针对运动中所存在的反向运动现象,从编队控制器中的动作选择策略层面提出了编队控制器起始阶段策略优化方法.在运动初始时,定义了等候条件与启动条件,对部分无人车进行延迟启动,仿真验证了该策略具有一定的能量节约作用,但可能会增加收敛时间.