超大型多模块结构组装过程动力学与姿态控制1)

符康琦 张乐榕 李庆军,2) 邓子辰 吴志刚 蒋建平

* (中山大学航空航天学院,广东深圳 518107)

† (西北工业大学航空学院,西安 710072)

引言

超大型航天结构的空间组装近年来受到高度关注[1-2].空间组装可以突破单次火箭发射体积和质量的限制,同时避免超大型结构在轨展开带来的技术挑战和风险.目前国内外研究机构已经提出多个空间组装大型航天结构的方案[3],包括空间太阳能电站[4-5]、太空望远镜[6]、人造重力航天器[2]等.

超大型航天结构的空间组装涉及长时间在舱外执行组装任务,有些任务需要在高轨、甚至在深空执行,完全依赖航天员执行空间组装任务是不现实的,因此使用机器人执行超大型结构的空间组装任务成为必然[7].目前已有成熟的空间机器人理论和技术[7-9],所以机器人技术不作为本文的研究重点.机器人在空间环境下组装超大型、多模块结构面临许多难题,其中动力学与控制是研究组装过程动力学特性、掌握控制规律和设计组装方案的基础,是空间组装的关键问题之一[1].然而,超大型、多模块结构的空间组装过程需要通过机器人对模块进行抓捕、运输、位姿调整、安装和锁定等重复操作[5],同时,组装过程系统参数随时间发生变化,给动力学与控制带来新的挑战.

目前,国内外针对航天器空间组装的研究大多集中在概念论证、方案设计、机器人控制、模块与结构设计等方面,针对组装过程动力学与控制的研究较少.Badawy 等[10]针对大型航天结构的模块自组装过程,提出了基于人工势场法的位置和姿态控制方法.Chen 等[11]针对多个柔性航天器自组装过程,采用浮动坐标法建立了柔性航天器的刚柔耦合动力学模型,通过椭圆描述航天器的人工势场,实现了柔性航天器的自组装和防撞控制.然而,文献[10-11]的方法要求模块具有自主感知和控制的能力,而超大型多模块结构的组装则需要机器人执行,这两种组装方式面临不同的动力学与控制问题.Boning 等[12]针对机器人群体空间组装大型柔性结构的过程,建立了系统的动力学模型,基于机器人高频控制与结构低频控制相解耦的控制策略,设计了机器人群体的协调控制系统,完成组装任务的同时降低了结构振动.杨胜丽等[13]针对三分支机器人在空间柔性结构上爬行的问题,将结构等效为悬臂条件的欧拉-伯努利梁,建立了机器人-结构系统的刚柔耦合动力学模型,研究了降低结构振动的机器人爬行步态优化方法.然而,文献[12-13]采用了线性模态方法将结构的动力学方程转化为常微分方程,难以推广到大柔性、刚柔耦合的空间结构.

从动力学建模的角度而言,空间组装过程既包含轨道、姿态等刚体运动,也包含组装模块的结构振动,同时还包含空间机器人的复杂操作,导致系统的动力学模型非常复杂.在这种情况下,基于绝对坐标的方法是一种比较合适的建模方法,包括描述刚体的自然坐标法[14]和描述柔性体的绝对节点坐标法[15].这两种方法在同一个全局坐标系下描述刚体的位置和姿态、柔性体节点的位置坐标和位置梯度,完全通过笛卡尔坐标描述系统的大变形和任意转动,适合用于构型复杂的刚柔耦合系统动力学建模.Li 等[16]针对卫星天线的组装过程,采用自然坐标法和绝对节点坐标法建立了卫星本体-机械臂-组装模块的动力学模型,研究了减小机械臂操作过程对卫星本体姿态干扰的轨迹优化方法,通过动力学仿真验证了建模和轨迹规划方法的有效性.荣吉利等[17]基于自然坐标法和绝对节点坐标法对大型桁架展开和组装过程进行了动力学仿真,并与ADAMS和ANSYS 软件结果进行了对比,分析了组装时间、组装机构阻尼系数和刚度系数对组装过程的影响.然而,文献[16-17]没有考虑空间环境干扰力对组装过程动力学的影响.Li 等[18]基于矩阵直积推导了适用于所有绝对节点坐标法单元的分布式万有引力(包含万有引力梯度)表达式,提出了基于绝对节点坐标法的航天器轨道-姿态-结构耦合动力学建模方法.王启生等[19-20]针对机器人组装大型梁结构的过程,采用自然坐标法和绝对节点坐标法建立了主结构-机器人-待组装结构耦合的动力学模型,分析了组装过程的轨道-姿态-结构耦合动力学响应.在此基础上,Yang 等[21]基于准静态、小变形等假设推导了该过程的结构振动、夹持机构受力、机器人关节控制力矩的解析解,研究发现万有引力梯度和科氏力对组装过程产生重要影响,且组装过程的结构振动幅值至少随梁长度的4 次方增长.然而,上述文献只研究了单次模块安装过程,而没有研究超大型结构多次模块安装过程的动力学行为.

超大型、多模块结构的空间组装过程中,结构构型和尺寸将随着组装进程逐渐增长.针对该特点,王恩美等[22]在有限元方法的基础上提出了节点自由度加载方法,用于描述系统自由度逐渐增加的过程.他们在另一篇论文中针对该过程的结构振动问题,提出了分布式自适应振动控制方法,实现了控制器数量逐渐增加的结构振动抑制[23].Cao 等[24]研究了圆环形支撑结构的空间组装过程,基于相对轨道运动方程、有限元模型和车桥耦合模型,建立了系统的动力学方程,并研究了不同组装策略下的动力学响应.罗建军等[25]针对机器人搭建空间桁架的过程,进行了动力学建模、运动序列规划、装配序列规划和机器人控制等方面的研究.然而,文献[22-25]没有考虑空间环境干扰力带来的影响.超大型结构具有尺寸超大、柔性超大等特点,在空间环境干扰力作用下会出现大幅振动、结构失稳、轨道-姿态-结构耦合等复杂动力学行为[26-28].文献[21]研究表明,不考虑万有引力梯度或科氏力将导致低估结构振动幅值和空间机器人的控制力矩.

本工作针对从单个模块到千米量级结构的空间组装过程,基于自然坐标法和绝对节点坐标法提出了一个考虑空间摄动的动力学分析、规划与控制的仿真框架,建立了考虑万有引力梯度和科氏力的主结构-机器人-组装模块组合系统的轨道-姿态-结构耦合动力学模型,开展了机器人的运动规划、轨迹规划和控制器设计研究,分析了不同俯仰姿态角和姿态控制方案下的组装过程动力学特性,以期为超大型航天结构的组装方案设计提供参考.

1 问题描述

本工作旨在提出一个基于绝对坐标方法的机器人组装超大型、多模块结构的轨道-姿态-结构耦合动力学与控制仿真框架,并以组装长度为1600 m 的梁结构为例开展动力学仿真与姿态控制研究.在此算例中,机器人在轨道上以给定姿态逐个组装长度为100 m 的梁模块,如图1 所示.为了提高仿真效率,本文只研究组装过程系统在轨道平面内的运动,后续研究中可以通过将平面单元更换成三维单元将本文的研究思路和方法拓展到三维情形.

图1 机器人空间组装超大型多模块结构示意图(以质心为基点将组装系统放大了50 000 倍)Fig.1 Conceptual drawing of the robotic assembly of an ultra-large multi-modular structure in space (the assembly system is magnified by 50 000 times form the center of mass for clearness)

组装系统由机器人、主结构(已完成的部分)和组装模块(未完成的部分)组成,其中机器人采用双臂构型,每个机械臂在轨道平面内具有3 个关节自由度和1 个夹持机构.由于空间机器人的刚度远远大于超大型结构,所以将空间机器人简化为多刚体系统,主结构和组装模块简化为欧拉-伯努利梁.在仿真中考虑轨道运动引起的科氏力和分布式万有引力梯度,研究不同组装姿态和控制情形下的动力学特性.

机器人组装超大型多模块梁的轨道-姿态-结构耦合动力学仿真框架如图2 所示.首先,从动力学模型的角度出发,用自然坐标法和绝对节点坐标法建立空间机器人、主结构和组装模块的刚柔耦合动力学模型,其中主结构由多个组装模块连接而成.建立对接机构和机器人夹持机构的等效模型(包括对接过程、夹持机构抓紧和松开过程的参数变化),考虑空间摄动因素的影响,得到组装系统的轨道-姿态-结构耦合动力学模型.通过数值算法求解微分-代数方程,从而得到系统的动力学响应.

图2 轨道-姿态-结构耦合仿真框架Fig.2 Orbit-attitude-structure coupled simulation framework

从空间机器人的角度来看,需要获得下一个组装模块的属性,例如组装位置、组装方向和约定的抓捕地点等信息.随后,进行操作序列规划、动作序列规划和笛卡尔空间轨迹规划,最终转化到关节空间的轨迹.此外,通过反馈控制算法使空间机器人的关节跟踪给定轨迹,完成组装过程.除了机器人控制之外,主结构和组装模块根据实际情况可能需要轨道、姿态和结构等方面的控制.

最后,从仿真程序整体的角度,需要首先设计超大型多模块结构的组装序列,给每一个组装模块赋相应的属性.然后,在给定时间和地点生成新的组装模块(模拟运输机器人将组装模块运输到给定地点),进入机器人组装阶段,直到组装完成.

2 轨道-姿态-结构耦合动力学建模

本节简要介绍组装系统的轨道-姿态-结构耦合动力学建模方法,详细建模过程可参考文献[19-21].首先建立全局惯性坐标系OXY,坐标原点在地球质心,如图1 所示.

2.1 自然坐标法与绝对节点坐标法

在轨道平面内运动的刚体具有3 个自由度,为了简化多刚体的建模过程,采用自然坐标法建立空间机器人的动力学模型.空间机器人具有7 个刚体和9 个自由度.平面刚体的自然坐标法有两类形式,一种是采用4 个广义坐标的表示方法,含有1 个约束,例如两点格式;另一种是采用6 个广义坐标的表示方法,含有3 个约束,例如两点一矢格式.为了便于快速拓展到三维情形,本文采用两点一矢格式,如图3 所示,刚体AB 的广义坐标为[14]

图3 平面刚体的自然坐标法[21]Fig.3 Natural coordinate formulation of a planar rigid body[21]

其中rA和rB分别为A点和B点的全局坐标,v1为固连于刚体且垂直于刚体的单位矢量.由于eAB有6 个分量,而刚体AB 只有3 个自由度,所以eAB将受到以下3 个约束

其中l1为A点和B点之间的距离.为了描述刚体内任意一点在OXY中的坐标,采用以下插值

其中局部坐标系Ax1y1固连于刚体,且x1轴指向B点,C(x1,y1) 称为刚体的形函数.

对于柔性组装模块,采用一维二节点的欧拉-伯努利绝对节点坐标法梁单元进行建模,单元的广义坐标为

其中xe为梁的弧长坐标,le为梁单元的长度.单元中轴线上任意一点的全局坐标可表示为

其中,S(xe) 为3 次插值的形函数,具体形式参见文献[15].

通过约束Hamilton 方程可获得组装系统的动力学模型,其中的动能和弹性势能表达式见文献[14-15].为了模拟组装系统的轨道和姿态运动,还需要考虑刚体和柔性体的万有引力势能.自然坐标法和绝对节点坐标法都具有相同的描述形式,即式(3)和式(5)都是通过形函数和广义坐标获得刚体/柔性体单元内任意一点的全局坐标,而且形函数C(x1,y1) 和S(xe)都可以表示为一个行向量与单位矩阵的直积形式[18].因此,文献[18]提出了一种适用于自然坐标法和所有绝对节点坐标法单元的万有引力广义力表达式,并已经包含了万有引力梯度的作用.

为了推导组装系统的动力学模型,需要将组装系统的所有广义坐标写成一个广义坐标向量q,其中包括空间机器人7 个刚体和16 个组装模块.这些组装模块共包含 16×4(n+1) 个广义坐标(n为每个组装模块的单元数,取n=5).对于空间机器人,虽然每个刚体具有6 个广义坐标,但7 个刚体之间有6 个点可以共用,所以空间机器人共有30 个广义坐标.组装系统的动力学模型为

其中,M为系统的质量矩阵,p称为广义动量,λ 为Lagrange 乘子,g(q) 为系统的所有约束,U(q) 包含了系统的万有引力势能和弹性势能,Q是广义外力向量.广义外力包括夹持机构、对接机构对机器人和组装模块的力,以及机器人对组装模块的控制力,可通过虚功原理获得.

在此模型中,所有刚体和柔性体的万有引力和万有引力梯度已经包含在 ∂U(q)/∂q中.通过给定合适的轨道和姿态初始条件,即可实现动力学仿真.系统的轨道-姿态-结构耦合效应体现在两方面: 一方面是物体所受的外力是分布式的,将同时对轨道、姿态、结构产生影响;另一方面则是计算这些分布式外力时,需要同时用到系统的轨道、姿态和结构的状态.在图1 所示的组装场景,柔性结构保持指向地面的姿态,即结构随轨道运动发生旋转,因此结构组装时沿径向运动的过程会存在科氏力.科氏力已经包含在方程(6)的惯性力中,无需额外考虑.

2.2 夹持与对接机构的接触碰撞

除了机器人和组装模块的动力学模型以外,动力学仿真过程还需要包含机器人末端夹持机构、组装模块之间对接机构的动力学模型.在超大型多模块结构的组装过程中,夹持与对接机构存在接触、摩擦、碰撞等典型的非光滑动力学行为,其动力学特性与接触面的具体形状有关,准确建模过程非常复杂[29],不是本文关注的重点.

本文采用传统的Kelvin-Voigt 线性弹簧阻尼模型等效夹持机构和对接机构的动力学行为.对于机器人的夹持机构,假设组装模块上已有可供夹持的抓手,能与夹持机构紧密配合,完成夹持后能提供平面内两个方向的力和一个力矩,则机器人末端受到的夹持力和力矩可表示为

式中,Δr为机器人夹持机构和组装模块夹持抓手形心之间的相对位置矢量,α 为两者的相对转角,kF,cF和kM,cM分别为对应的弹性系数和阻尼系数.弹性系数和阻尼系数在实际工程中可通过实验测得,在本文的数值仿真中,通过多次调试决定选择数值为kF=kM=1000 和cF=cM=3000 (采用国际单位),使夹持误差较小且对仿真步长的影响较小.同理,对接机构的弹性系数和阻尼系数都选为1000.

夹持机构的等效动力学模型在数值仿真中还需要处理松开状态和夹紧状态之间的切换.机器人爬行时,其中一个机械臂的夹持机构处于松开状态,当其遇到下一个抓手时需要切换为夹紧状态.为了在仿真程序中描述这个过程,需要处理两个问题.一是夹持机构形心与抓手形心在数值仿真中不可能完全重合,难以确定何时切换;二是如果切换状态时kF和cF从0 突变成1000 和3000,势必造成夹持力和力矩的突变,引起系统不稳定.针对这两个问题,本文给出简化处理方法: 首先,规定机器人在完成给定轨迹后立即开始切换(此时 Δr和 α 均不为0);然后,规定kF和cF经过2 s 从0 线性变成1000 和3000,从夹紧状态到松开状态时kF和cF经过2 s 从1000 和3000 线性变成0.通过这两种简化处理方法,避免了切换过程力和力矩突变而引起的数值发散问题.对接机构锁定过程的处理方式与夹持机构相同,锁定过程时间为10 s.

至此,已经建立了组装系统的轨道-姿态-结构耦合动力学模型,可以采用文献[30]的保能量-保约束算法进行数值求解.然而,这种做法将空间机器人和所有组装模块的动力学方程当作一个非常高维的微分-代数方程组进行求解,其中每一步都需要采用Newton-Raphson 迭代法求解离散的高维代数方程组,需要多次求系统受力及其雅克比矩阵,导致数值仿真效率极低.为此,本文提出一个简化处理方法: 对于夹持机构而言,夹持力和力矩认为与上一时间步的夹持误差及其导数成正比,因此在当前时间步可以将其视为常力和常力矩.通过该简化方法,在当前时间步,空间机器人和16 个组装模块变成了相互独立的动力学模型: 空间机器人的动力学方程是包含30 个广义坐标的二阶微分-代数方程(每一步仍需迭代),每个组装模块的动力学方程是包含4(n+1)个广义坐标的二阶常微分方程(不需要迭代).这些独立的动力学模型可以单独求解,还可以方便地实现并行计算,提高数值仿真效率.该方法的合理性将在后续动力学仿真中讨论.

3 轨迹规划与控制系统设计

通过上述动力学模型和数值求解,可以实现组合系统的轨道-姿态-结构耦合动力学仿真,但是机器人还无法实现组装任务.为此,本节给出空间机器人的轨迹规划、控制器设计以及主结构和组装模块的姿态控制.

3.1 空间机器人组装规划

为了完成组装任务,首先需要设计组装序列,现有文献中已有大量组装序列设计方法研究[25,31-32].本文的算例较为简单,采用逐个模块依次组装的序列,且空间机器人针对每个模块都采用相同的抓捕、稳定、安装、锁定和爬行的操作序列,如图4所示.下面介绍每一种操作的动作序列及轨迹规划过程.

图4 机器人组装一个模块的操作序列Fig.4 Operation sequence planning of the robot to assemble a module

(1) 抓捕操作

首先,假设组装模块处于完全展开的状态,且通过运输机器人已经按给定姿态运输到指定地点.为了简单起见,假设组装模块抓捕前与主结构处于共线状态,两者之间的距离为 (20-xcapt)m,其中xcapt为抓捕过程由于动量守恒导致主结构向后退的距离.

抓捕之前,机器人已位于主结构的下一个安装点处.抓捕过程中,机器人将前臂伸出,且保证夹持机构最终以垂直于梁轴线向下的方向运动,直至到达抓手位置(上、下的定义是垂直于梁轴线且机器人所在的方向为上,前、后的定义是沿梁轴线且组装方向为前,如图1 所示).前臂伸出时,机器人本体向前移动的距离为前臂伸出距离的一半,使机器人在完成抓捕后保持对称的构型.前臂末端夹持机构抬高最大高度设为1 m.

(2) 调整与稳定操作

完成抓捕后,组装模块和主结构可能并非处于共线状态,如果在安装阶段需要对主结构和待组装结构进行姿态调整,则可能引起大型结构的低频振动,在无阻尼的太空环境下持续较长时间,影响组装效率和组装精度.为此,抓捕完成后需要先对主结构和组装模块进行姿态和位置的调整与稳定,使两者尽可能处于共线的状态并保持合适的距离,同时机器人可以调整自身的构型.在本文的算例中,组装模块假设每次都以共线的形式出现在给定地点,因此抓捕完成后只需要经过短时间的稳定操作,使主结构和组装模块共线,并保持20 m 的距离.

(3) 安装与锁定操作

在安装阶段,主结构和组装模块在机器人带动下相互靠近,直至对接机构发生接触、锁定.该过程不仅要求主结构和组装模块的距离按五次多项式从20 m 减小到0 m,还要求机器人质心到主结构的距离保持不变,以减小机器人引起主结构和组装模块的振动,具体的规划过程见文献[19-21].安装完成后,还需要预留时间实现锁定操作.

(4) 爬行操作

安装和锁定完成后,机器人需要采用如图4 所示的爬行步态从当前位置移动到下一个组装点.假设每一步爬行距离为20 m,需要通过5 步才能爬到下一个组装点.在爬行一步的过程中,机器人需要先松开前夹持机构、前臂伸出至下一个抓手处并夹紧,然后对后臂和后夹持机构作同样的动作.

在抓捕操作和爬行操作的前臂伸出过程中,同样也要求机器人质心到主结构的距离保持不变,规划思路与安装操作类似,分为前后方向和上下方向.在上下方向,首先用148 s 将H点的轨迹向上抬起1 m,然后用剩下的148 s 向下移动1 m;在前后方向,用290 s 将H点向前移动20 m,同时机器人本体向前移动10 m,使得剩下的6 s 时间内H点只有上下方向的运动而没有前后方向的运动,以保证夹持机构以垂直于梁轴线向下的方向运动.通过上述规划,得到了机器人组装超大型多模块结构过程的动作序列,如图5 所示.在实际工程中,机器人还需要进行感知、决策、实时规划等,可能无法在3710 s 的短时间内完成1 个模块的组装.为了提高仿真效率,对机器人的操作都作了简化处理,主要关注组装过程的动力学仿真.

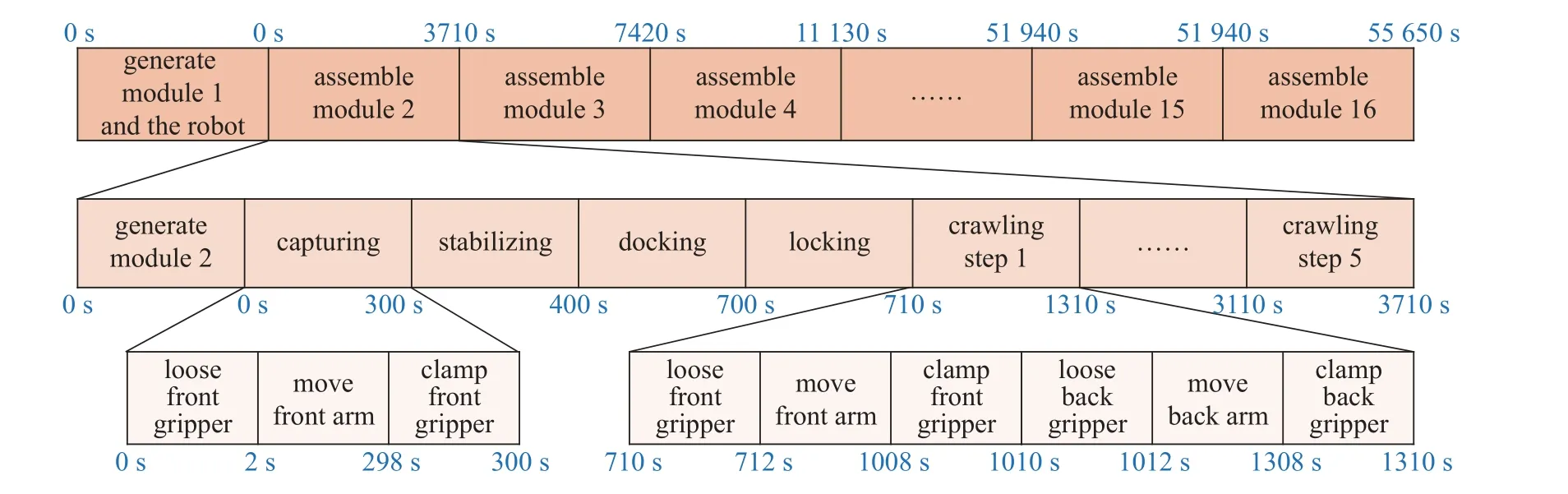
图5 机器人组装超大型多模块结构的动作规划Fig.5 Movement planning of the robot to assemble an ultra-large multi-modular structure

对于轨迹规划过程,先在笛卡尔空间采用五次多项式进行轨迹规划,然后通过几何关系转换到机器人关节空间.安装操作的笛卡尔空间轨迹规划及转换到关节空间的具体规划过程见文献[21].机器人在组装一个模块过程的关节轨迹如图6 所示,其中 θ1～ θ3和 θ5～ θ7表示的角度见图1.此外,θ4表示图1 中机器人本体DE 与机器人位置矢量的夹角,即俯仰姿态角.动力学仿真中将选取不同的 θ4.

图6 机器人组装一个模块的关节轨迹Fig.6 Joint trajectories of the robot assemblying a module

3.2 控制系统设计

为了完成规划的动作,机器人关节需要采用反馈控制跟踪规划好的轨迹.本文采用简单的PD 控制方法进行关节轨迹跟踪,对 θi,i=1,2,···,7 的反馈控制力矩可表示为

其中Kp=40 000 和Kd=5000 分别为比例和微分反馈增益(采用国际单位),ei=θi,p-θi为误差(下标p 代表规划的值),为ei对时间的导数.式(8) 中,i=4代表机器人本体的俯仰姿态误差和控制力矩.

除此之外,主结构和组装模块都需要进行控制.本文的算例中没有考虑轨道摄动力,不需要进行主结构的轨道调整,而且认为组装模块的轨道控制已由其他运输机器人完成.因此,主结构和组装模块主要进行姿态和结构控制.主结构和组装模块都属于超大型结构,可以采用分散式控制力矩陀螺进行姿态-结构联合控制[33].假设每个结构模块都具有若干个控制力矩陀螺,每个控制力矩陀螺将与共位布置的姿态传感器构成独立的PD 姿态反馈控制器(相邻的控制器没有信息交互),且比例增益为69 600,微分增益为835 200 (采用国际单位).动力学仿真考虑4 种姿态及控制情形.

(1) 情形1: 组装过程中主结构和组装模块的俯仰姿态角均为0,如图1 所示.由于此时系统的姿态角是万有引力梯度稳定的,所以不进行姿态控制.

(2) 情形2: 假设每个组装模块具有6 个均匀分布在模块上的PD 姿态反馈控制器,相邻控制器相隔20 m,如图7 所示,其余状态与情形一相同.

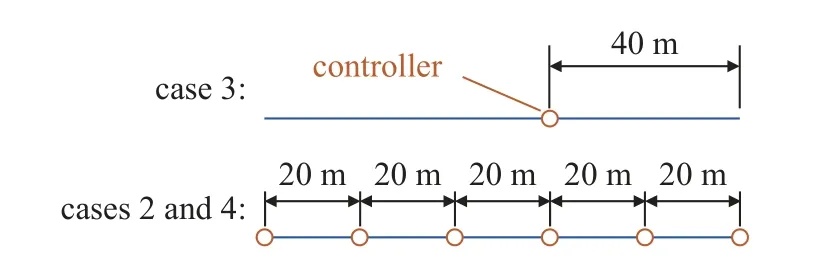
图7 姿态控制器布局Fig.7 Placement of attitude controllers

(3) 情形3: 组装过程中主结构和组装模块的俯仰姿态角均为 π/2 .由于此时系统姿态不稳定,所以需要采用控制力矩陀螺进行姿态控制,假设每个模块具有1 个PD 姿态反馈控制器,放置在距离前对接点40 m 处.

(4) 情形4: 假设每个组装模块具有6 个均匀分布在模块上的PD 姿态反馈控制器,相邻控制器相隔20 m,其余状态与情形3 相同.

4 轨道-姿态-结构耦合动力学仿真

通过上述动力学建模、轨迹规划与控制,即可实现机器人空间组装超大型、多模块结构过程的轨道-姿态-结构耦合动力学仿真.通过该仿真框架,可以研究不同组装方案(轨道、姿态、组装序列、机器人类型与数量等)、不同控制方案(推力器、动量交换装置、压电智能材料等)、不同的机器人和模块参数等对组装过程动力学响应的影响.本文主要研究不同的组装姿态和控制方案的影响.

采取与文献[21]相同的机器人与组装模块的几何、质量和刚度参数,每个模块的质量为3132 kg,抗弯刚度为EI=1.14×107N·m2;机械臂3 个连杆的长度分别为7 m,7 m 和2 m,两个机械臂(D点和E点)之间的距离为2 m,机器人总质量为3271 kg.第一个模块和机器人初始位于地球静止轨道,时间步长取为0.005 s,得到动力学仿真结果如图8～图17 所示.

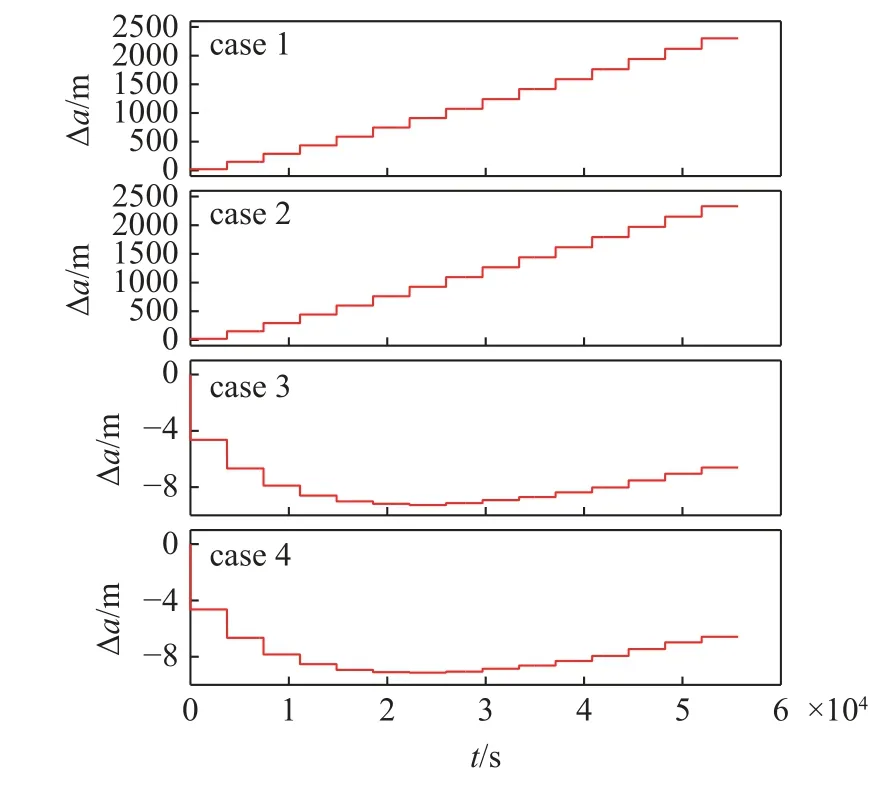
图8 组装系统质心的长半轴变化率Fig.8 Variation of the semimajor axis of the mass center of the assembly system

图8 和图9 分别给出了4 种情形下组装系统质心的轨道长半轴变化量和离心率.由图可知,情形1 的轨道长半轴在整个组装过程中呈现阶梯式增长的特点,每组装一个模块,长半轴都显著增加.值得注意的是,虽然超大型梁的长度仅为1600 m,在仿真中组装结束时刻的长半轴却比初始时刻增加了2301.4 m;一个组装模块的长度仅为100 m,生成模块3 后系统的长半轴却比生成模块3 前增加了129.5 m.这个现象与生成新组装模块的方法有关.本文认为只要模块生成成功了,就可以参与组装系统质心以及轨道的计算.生成一个新组装模块时,认为组装模块处于新组装点的正前方(对于情形1 是天顶方向,对于情形2 和情形3 是轨道运行速度的反方向).这种生成方式使得情形1 中组装模块的轨道高度比主结构和空间机器人更高;此外,对于圆形轨道,轨道高度越高,运动速度应该越小,而情形1 使新生成的组装模块与新组装点同步绕地心运动,即组装模块的运动速度比主结构和空间机器人更快.换句话说,新生成的组装模块的轨道为椭圆轨道.这两个方面的原因共同造成了情形1 的轨道长半轴和离心率快速增加.

图9 组装系统质心的离心率Fig.9 Orbital eccentricity of the mass center of the assembly system

为了验证上述机理,针对情形1 的模块3 组装前后进行对比.模块3 生成后,系统质心的轨道半径将增加Δr

其中,计算质心的参考点为模块2 的前对接点,此时机器人正好位于该点.由于主结构和组装模块的角速度相同,因此生成模块3 后,系统的角速度基本保持不变.因此,轨道半径的增长将导致线速度变化

根据轨道动力学知识可知

其中 ε 为单位质量的轨道运动机械能.由于 Δr和Δv均为小量,所以有

代入地球静止轨道的数据计算,得到结果为Δa=134.296 m,与数值仿真129.5 m 的结果接近,说明了上述机理的有效性.在式(12)的两项中,第1 项和第2 项各占约50%.

由于情形2 采取了与情形1 相同的姿态条件,所以其轨道长半轴和离心率变化情况与情形1 类似.对于情形3 和情形4,由于组装俯仰姿态角选择为 π/2,则新生成的组装模块与主结构几乎处于相同的轨道高度且具有相同的运行速度,所以轨道长半轴和离心率基本保持不变.这表明了不同的组装姿态下会出现不同的组装过程系统轨道跃变规律.

组装过程姿态角变化规律和姿态控制力矩如图10 和图11 所示,其中情形1、情形2 和情形4 的每个模块有6 个相距20 m 的姿态测量点,情形3 每个模块只有1 个姿态测量点.由于图10 和图11中曲线太多,为清晰起见,不再给出每条曲线对应的姿态测量点位置.由图可知,情形1 没有进行姿态控制,在机器人操作干扰和科氏力作用下,主结构和组装模块的姿态角逐渐增大,最终出现约3.2°的姿态误差.情形2 由于采用了姿态控制,所以姿态误差不超过0.1°,但是控制力矩出现了多次突然增大的情况.情形3 的组装姿态为不稳定的平衡点,每个模块采用了1 个PD 姿态控制器,在组装过程中姿态角都控制在0.4°范围内,但最大控制力矩达到了400 N·m,而且在机器人抓捕组装模块的瞬间会出现较大的姿态误差和控制力矩突变.相比而言,情形4 的姿态误差和控制力矩都仅为情形3 的 1/20 左右,在机器人抓捕组装模块瞬间也出现冲击突变的情况.此外,情形4 的姿态误差和控制力矩在时间为13 600 s,34 500 s,46 100 s 以及51 800 s 处出现振幅先增大后减小的“鼓包”现象.此时,姿态误差和控制力矩的值可大幅增加,例如情形4 在13 600 s 附近控制力矩的极大值为9095 s 附近极大值的3.2 倍.

图10 主结构和组装模块的姿态误差Fig.10 Attitude errors of the main structure and assembly module

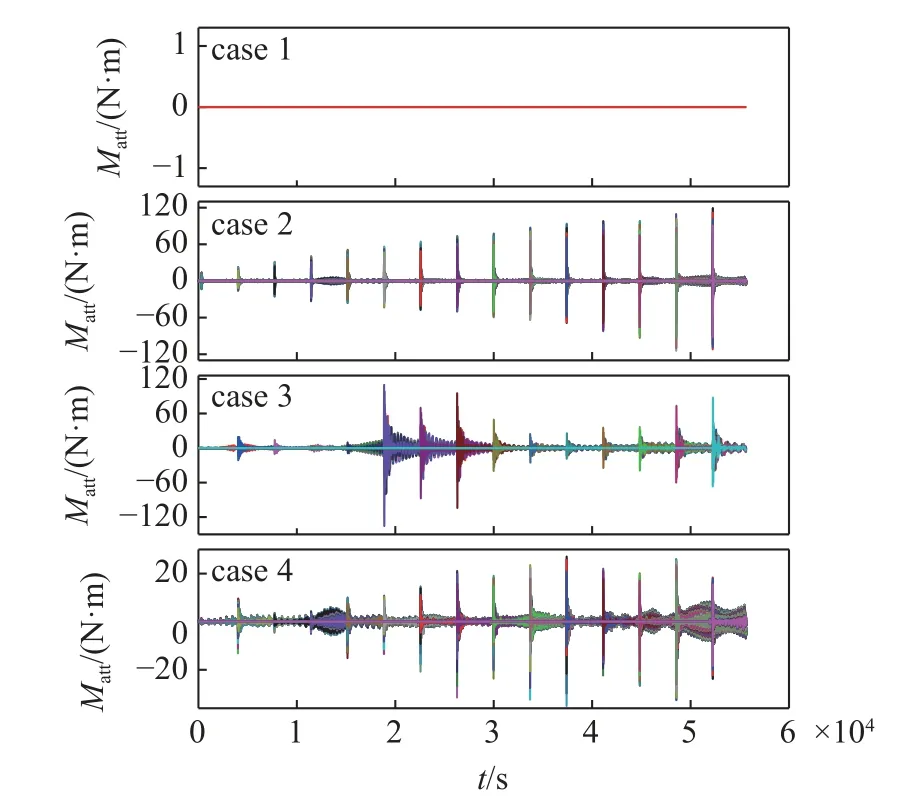
图11 主结构和组装模块的姿态控制力矩Fig.11 Attitude control moments of the main structure and assembly module

为了研究结构振动,首先需要定义一个局部的坐标系,不同的定义方法会得到不同的结构振动结果.为了简单起见,本文将局部坐标系原点定义在主结构模块1 的第1 个节点,其方向与梁在该点处的轴线相切,图12 给出了在此坐标系下主结构端点的振动情况.在组装过程中,主结构的长度逐渐增长,结构刚度快速下降,空间干扰力快速增加,而且机器人操作干扰力的作用点也逐渐远离系统质心,因此四种情形下的主结构末端点振动幅值也随着组装进程快速增长.对比不同的情形,情形1 的最大振动幅值达到51.8 m,情形2 为0.21 m,情形3 为2.51 m,而情形4 只有0.14 m,验证了情形2 和情形4 的分散式姿态和结构控制方法的有效性.

图12 主结构末端点的振动Fig.12 Vibrations of the main structure’s endpoint

图13 和图14 分别给出了4 种情形的机器人关节轨迹跟踪控制误差和力矩.由图可知,机器人关节的控制精度比较高,情形1 的关节误差小于0.6°,情形4 则小于0.1°.情形1 的最大控制误差出现在机器人抓捕和爬行过程.情形4 的最大控制误差和力矩出现在安装过程.夹持和对接机构刚度和阻尼系数改变的过程中,动力学响应取决于真实的夹持和对接机构动力学模型,无法反映真实情况.但是可以肯定的是,情形4 的姿态控制精度更高、结构振动幅值更小(如图10 和图12 所示),所以更容易实现柔顺抓捕,避免碰撞.

图13 机器人关节控制误差Fig.13 Control errors of joints of the robot

图14 机器人关节控制力矩Fig.14 Control moments of joints of the robot

除了夹持和对接机构刚度和阻尼系数改变的过程之外,爬行过程机器人关节的最大控制力矩大致为: 情形1 为35 N·m,情形2、情形3 和情形4 都为27 N·m;安装过程关节最大控制力矩大致为: 情形1 为97 N·m,情形2 为81 N·m,情形3 和情形4 都为67 N·m,如图15 所示.出现这种区别的主要原因在于,情形1 和情形2 的主结构和组装模块在万有引力梯度作用下会有相互分离的趋势,需要通过机器人维持两者之间的距离,并实现组装.此外,通过对比情形3 和情形4 的控制误差和力矩可知,姿态控制系统除了能有效抑制姿态误差和结构振动,还有利于减小空间机器人的控制力矩和控制精度;通过对比情形2 和情形4 可知,不同的组装姿态角对空间机器人的控制性能也有较大的影响.

图15 图 14 的局部放大图(组装模块16 过程)Fig.15 Zoom of Fig.14 (assembly of module 16)

图16 和图17 给出了机器人的两个末端夹持器的夹持误差和夹持力随时间变化情况.由图可知,抓捕过程和爬行过程中,当夹持器从松开状态切换成夹紧状态时,夹持器会有较大的冲击力.对于该状态切换过程,实际上夹持器的受力应该与夹持器和抓手的形状都有关,还受机器人控制算法的影响,是一个复杂的接触碰撞问题.在夹持器处于夹紧状态时,夹持器的受力来源于机器人的操作力、空间环境干扰力以及科氏力等.夹紧状态时,夹持器在安装过程的受力最大,情形1 安装过程受力最大值9.3 N,情形2 为8.7 N,情形3 为6.1 N,情形4 为6.6 N.通过数值仿真发现的另一个规律: 随着组装进程的发展,机器人关节的控制力矩和末端夹持器的受力都逐渐增大.以情形4 为例,组装模块2 时,关节最大控制力矩为30.0 N·m,末端夹持器最大只需要2.1 N 的夹持力;到组装模块16 时,关节最大控制力矩为66.7 N·m,末端夹持器的最大夹持力为6.6 N.

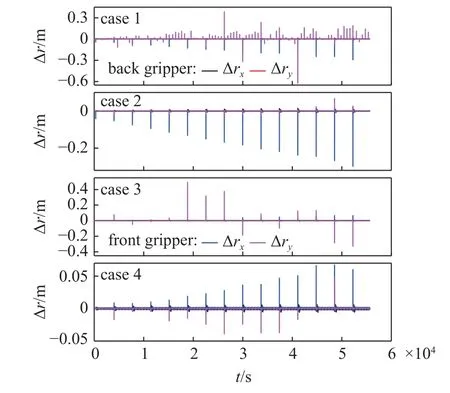
图16 末端夹持器夹持误差Fig.16 Grasping errors of the grippers

图17 末端夹持器受力Fig.17 Forces on the grippers

从图16 可以看出,空间机器人在抓捕、爬行过程中完成移动前臂或后臂的动作后,末端夹持机构并没有与抓手重合,而是存在一定的距离(情形1 小于0.6 m,情形2 小于0.3 m,情形3 小于0.4 m,情形4 小于0.05 m),然后在数值仿真中将末端夹持器从松开状态切换成夹紧状态,从而产生了虚拟的夹持冲击.正是由于这种虚拟的夹持冲击,使得采用了相同姿态控制方案的情形2 和情形4 表现出不同的姿态控制效果和结构振动幅值.在实际工程中,机器人移动机械臂的过程应加入视觉、触觉等反馈控制,避免夹持机构与抓手、结构发生碰撞,实现柔顺抓取.

最后,为了验证夹持力和力矩在当前时间步等效为常力和常力矩的合理性,采用不同的时间步长对情形4 进行了对比.图18 给出了夹持器的夹持误差和夹持力的时间历程(为了清晰只给前295 s 的结果).本文采用了Runge-Kutta 方法求解系统的动力学方程,当夹持力和力矩在当前时间步为常数时,该算法针对夹持机构模型退化为显式Euler 格式.由图18 可知,夹持误差和夹持力都表现为非常低频的动力学行为,在非常小的时间步长下显式Euler 格式仍然有比较高的精度.同时,不同的时间步长求解得到几乎相同的动力学仿真结果,这也表明了夹持力和力矩在当前时间步等效为常力和常力矩具有可行性.

图18 不同时间步长夹持误差和夹持力Fig.18 Grasping errors and forces using different time step size

综上所述,情形1 采取了万有引力梯度稳定的组装姿态,且没有进行姿态控制,虽然姿态角误差在组装过程只有2°,但引起了大幅结构振动,导致机器人操控过程面临夹持器与组装模块碰撞的风险.即使在稳定夹持期间,由于主结构和组装模块受万有引力梯度的影响,安装过程和爬行过程都需要更大的关节控制力矩和末端夹持力.情形2 在情形1 的基础上加入了较多的姿态控制器,虽然姿态误差和结构振动幅值都下降了1 个数量级.但是由于组装模块的轨道和主结构轨道不同,情形1 和情形2 的组装过程还面临较大的轨道漂移.因此,情形1 和情形2 的万有引力梯度对组装过程的姿态控制力矩、机器人控制误差和力矩、末端夹持器受力等结果产生重要影响.情形3 和情形4 采取了万有引力梯度不稳定的平衡点,因此组装过程基本不受万有引力梯度的影响.情形3 的姿态控制误差和结构振动都比情形4 大一个数量级,末端夹持器碰撞的风险较大.情形4 的姿态和结构振动控制效果最好,但仍然需要加入机器人的柔顺控制,因为0.05 m 的末端误差和0.1 m 的结构振动也会导致夹持器与组装模块的碰撞.

5 结论

针对机器人空间组装超大型、多模块结构的过程,发展了考虑空间摄动和接触碰撞的轨道-姿态-结构耦合动力学仿真框架,研究了不同俯仰姿态角和姿态控制方案下的组装过程动力学响应.研究发现,当主结构和组装模块处于不同轨道时,组装过程引起的长半轴变化量可能超过模块的长度,这是由质心变化和轨道差异共同引起的;这说明组装过程中系统的轨道参数跃变规律取决于组装姿态.在姿态方面,虽然万有引力梯度在一定程度上能保持姿态稳定,但由于机器人操作干扰和科氏力影响,必然导致姿态摆动.如果不加以控制,则会导致大幅结构振动,增加了机器人末端夹持器与结构、抓手的碰撞风险,影响组装的精度和效率.从机器人控制的角度而言,机器人完成给定操作后,与抓手仍然存在一定的距离(未接触到结构或已嵌入到结构中).为了降低碰撞风险,需要采用柔顺控制策略,实时检测抓手和结构的位置和速度,通过实时的轨迹规划和反馈控制进行更精准的抓取操作,以实现在振动的结构上柔顺操控的目的.

未来的研究计划包括两方面.一方面是继续完善此仿真框架的内容,包括将动力学模型拓展到三维情形、精确描述组装过程的接触碰撞、发展高效的并行求解程序、考虑机器人运输过程和组装模块展开过程等;另一方面,可基于此仿真框架,研究不同组装方案对动力学特性的影响规律,例如不同的超大型结构、组装序列、轨道姿态方案、控制方案、机器人类型及数量等.