上承式钢管混凝土拱桥拱脚局部应力分析

石桦睿

长沙理工大学 湖南 长沙 410114

钢管混凝土拱桥的拱脚是整座桥梁中至关重要的一部分，它在施工过程中和成桥后承担着不同的重要作用。对于上承式钢管混凝土拱桥，拱脚主要承受轴力和弯矩的作用，又由于拱脚处受力比较复杂，而拱脚处的计算分析对此处裂缝的预防和控制起着关键作用，近年来相关学者对拱脚处进行了一系列研究。张栋培[2]采用程序算法建立拱脚局部模型，分析不同温度工况下拱脚局部应力的变化情况，得到温度对拱脚应力变化的影响，并由此提出控制拱脚开裂的措施；姜自奇[3]利用Midas civil建立了变截面钢管混凝土桁架拱桥及其拱脚三维模型，对拱脚进行了在外荷载以及结构自重作用下的应力分析，并提出拱脚抗裂的预防措施；马坤全[4]采用8节点任意六面体等参单元建立了拱脚局部模型，并分析了拱脚在主力荷载作用下空间应力分布特性，最后与实验结果基本一致。综合以上论述，国内大多研究都是在既定情况下对拱脚进行的应力分析，而在桥梁施工过程中对拱脚局部应力分析的研究较少。在施工工程中对拱脚的应力进行实时监控和验算有利于对施工时拱脚裂缝的产生起到防治作用。基于此种不足，本文对施工过程中最不利荷载工况下的拱脚局部应力进行分析。

1 工程总体概况

1.1 工程概况

本文选取涂乍河特大桥作为研究对象，该桥净跨252m，两侧桥跨分别为2×35m的上承式钢管混凝土拱桥，桥面系布置为先简支后连续的连续T梁，桥面总宽度为12m，主拱圈采用两条对称拱肋，整座桥横跨涂乍河，左侧为保靖侧，右侧为涂乍侧。总体布置图如图1所示。

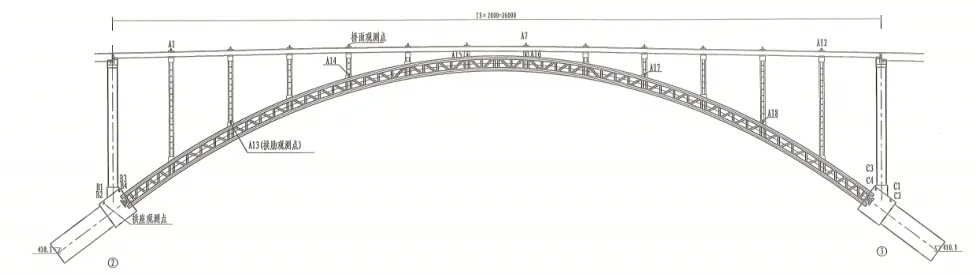
图1 桥梁总体布置图

1.2 拱脚结构

拱脚主要由以下几个部件构成：拱座、预埋钢管、连接钢管、上部钢管、封脚处混凝土以及钢管内部灌注混凝土。其中，拱座和封脚混凝土采用C55混凝土，上、下弦杆以及腹杆和横撑均采用Q345钢材，钢管内部泵送C55混凝土。根据对称性，取保靖侧上游处拱脚进行研究分析，拱脚处各控制截面如图2、3所示。

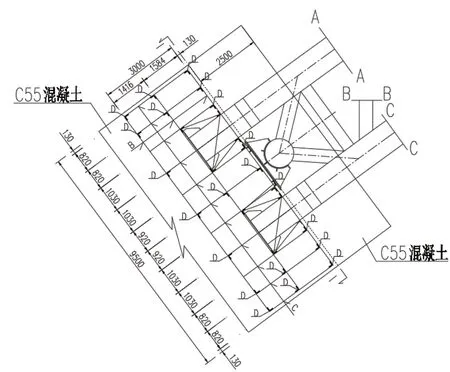
图2 拱脚细部构造

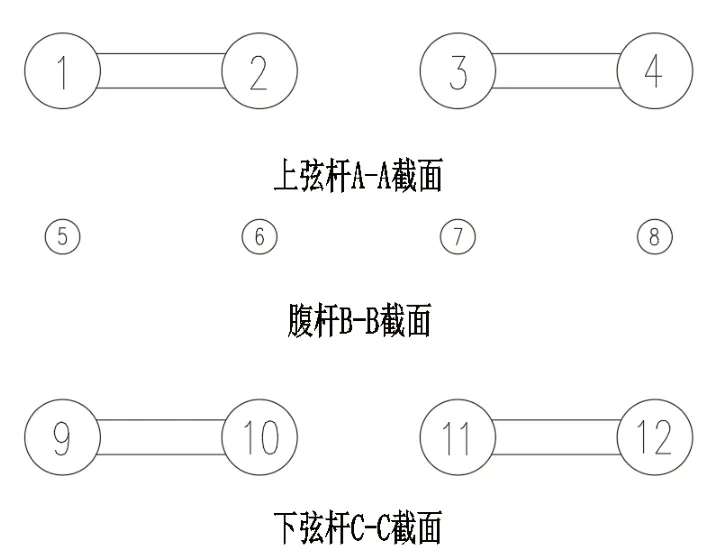
图3 拱脚控制截面

2 建立有限元模型

2.1 有限元模型

采用Midas civil建立全桥的有限元模型，全桥主要采用梁单元模拟，索单元采用桁架单元模拟，全桥一共划分为15个施工阶段，拱脚在封脚前采用铰接模拟，封脚后采用固结模拟，交界墩采用固结模拟，其他内部连接采用弹性连接中的刚性连接模拟。采用Midas FEA 建立拱脚的局部模型，利用混合四面体网格划分实体单元，拱座底部采用固结模拟，拱脚端部上、下弦杆和腹杆控制截面处采用刚性连接模拟。模型如图4、5所示：

图4 全桥有限元模型

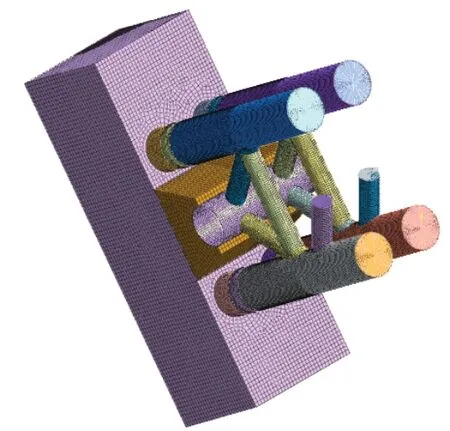
图5 拱脚局部模型

2.2 最不利荷载工况的确定

从Midas civil中按照施工阶段依次提取出1、2、5、6、9、10号截面的轴力和弯矩，不同施工阶段的弯矩和轴力变化图如下图6所示。由图可知，随着施工阶段的变化，上弦杆弯矩和轴力总体呈现逐渐变大的趋势，下弦杆的轴力和弯矩也是逐渐变大，腹杆的弯矩和轴力变化幅度不大。为了研究封脚前后的最不利工况[5]，选取灌注钢管混凝土为工况一，完成二期铺装为工况二。

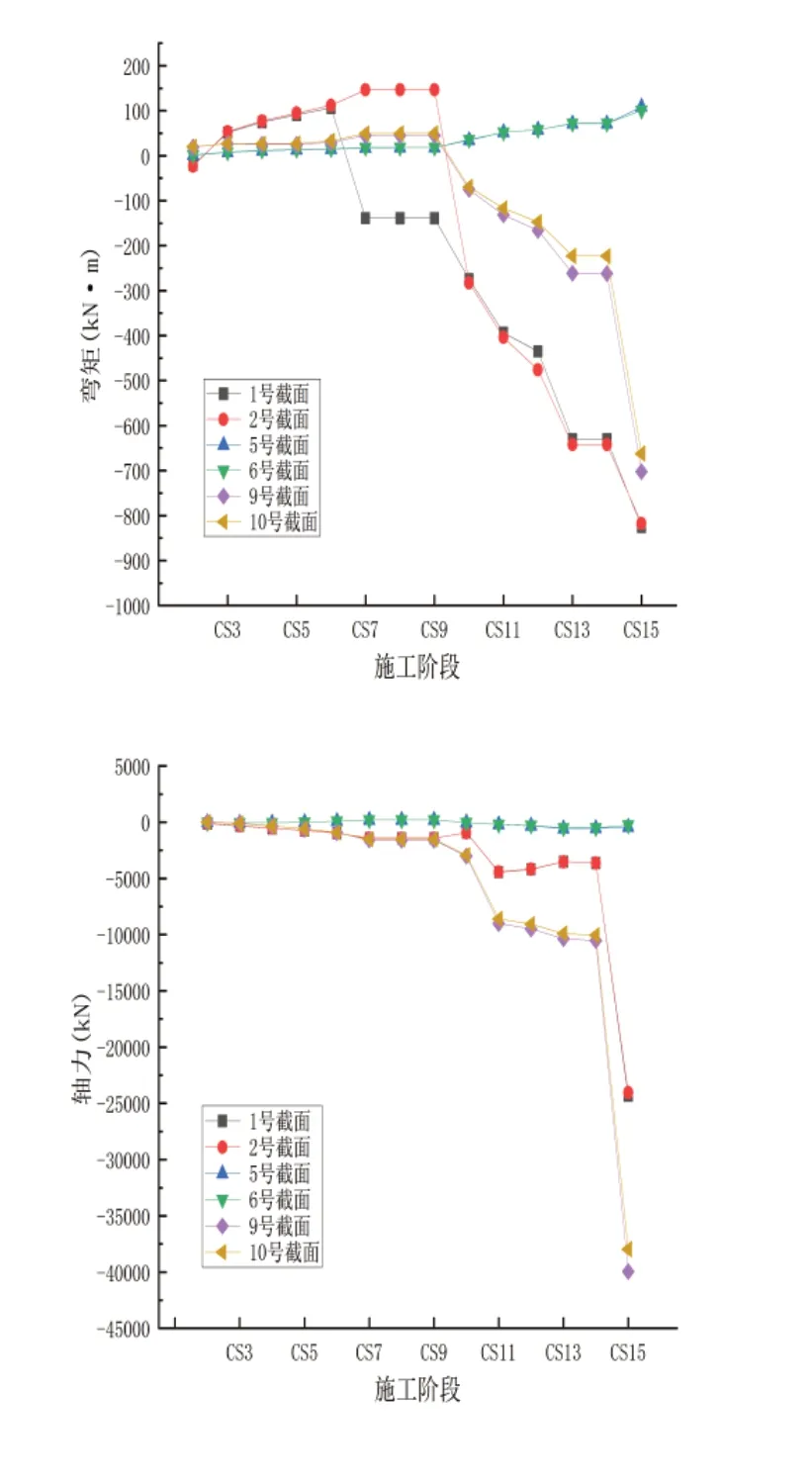
图6 弯矩/轴力变化图

图7 工况一拱座最大拉、压应力

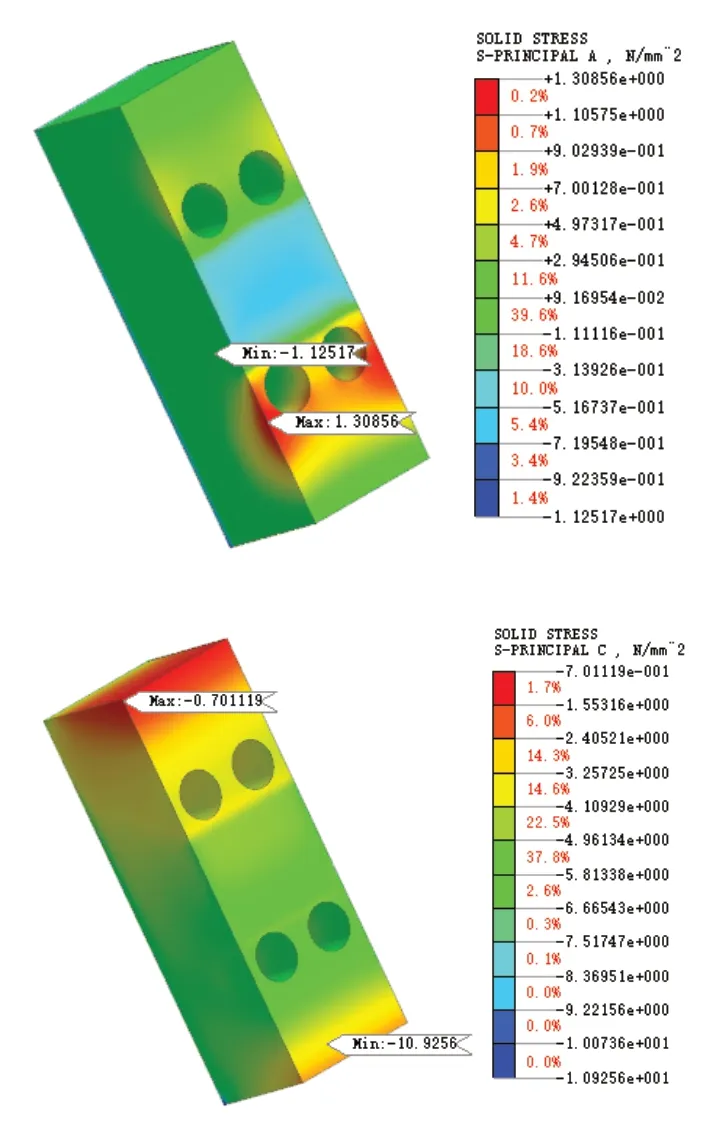
图8 工况二拱座最大拉、压应力

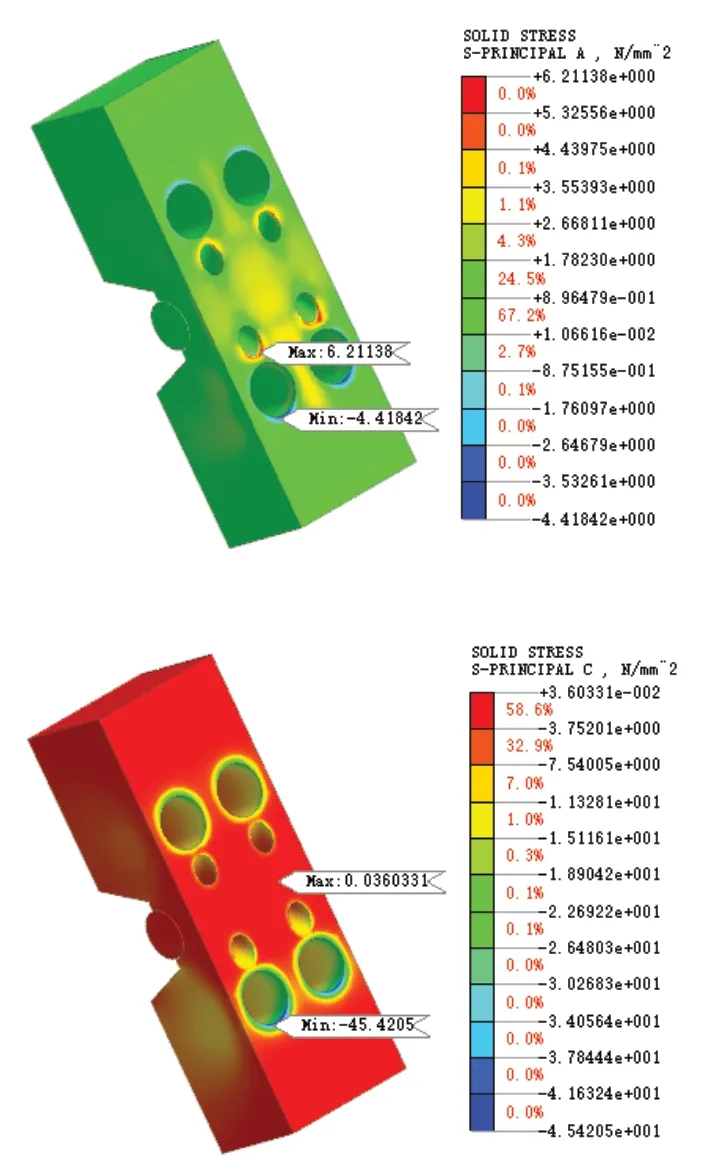
图9 工况二封脚混凝土最大拉、压应力

根据已选择的工况，从Midas civil里提取出1、2、5、6、9、10号截面的内力，如下表所示。局部模型中荷载的方向应与整体模型中的荷载方向保持一致，确保拱脚局部受力与整体模型中保持一致。

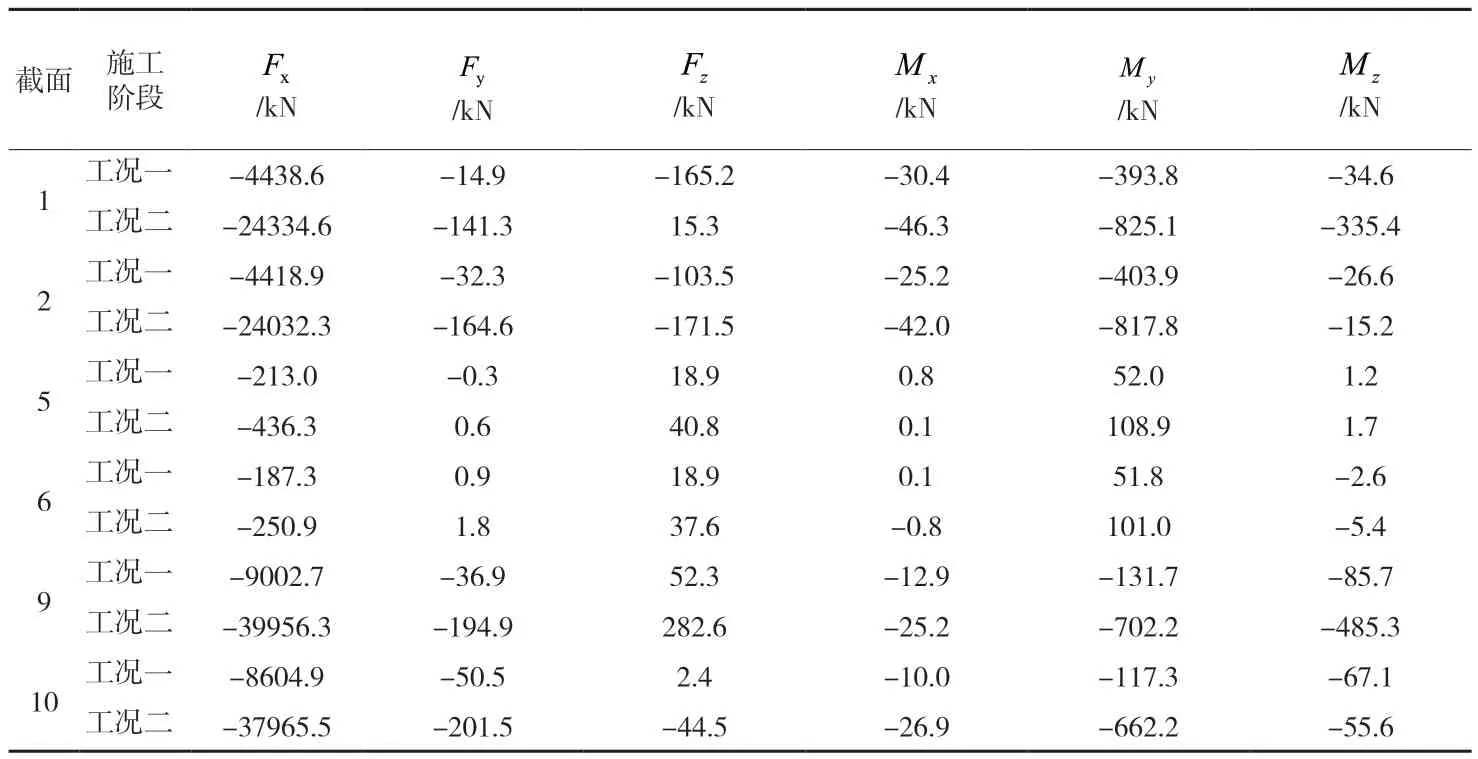
表1 控制截面内力

3 各工况应力计算分析

3.1 工况一计算结果

混凝土作为一种脆性材料，满足脆性破坏理论，在分析过程中主要采用第一强度理论，即最大拉应力理论来判断拱脚处混凝土的最大拉应力是否超过规范规定的混凝土抗拉强度标准值，若混凝土的最大拉应力不超过混凝土本身的抗拉强度标准值，则材料不会发生断裂。钢材的应力分析不同于混凝土，在FEA中主要查看Von Mises应力，Von Mises应力以第四强度理论为基础，综合考虑第一、第二、第三主应力的一种等效应力，其本构模型在分析金属材料的疲劳和破坏中应用较多，因此用于分析钢材应力[6]。由于篇幅限制，本文仅列举出拱座混凝土最大拉应力、最大压应力的应力分析结果，如下图所示（正值表示拉应力，负值表示压应力，单位：MPa）。

由上述计算结果分析可知，拱座的最大拉应力为2.34MPa，位于预埋段钢管与拱座交接处；最大压应力为-10.80MPa，同样位于预埋段钢管与拱座交接处。由于拱座的最大拉应力未超过文献[1]所允许的应力值，所以拱脚应力符合要求，不会发生断裂。

3.2 工况二计算结果

工况二结果为拱座混凝土和封脚混凝土最大拉应力、最大压应力的应力分析，如下图所示。根据结果分析可知，拱座的最大拉应力为1.31MPa，位于拱座上表面左下方棱边处；最大压应力为-10.93MPa，位于拱座上表面下方棱边处。封脚混凝土的最大拉应力为6.21MPa，位于腹杆与拱座交接处，超过规范所允许的混凝土抗拉强度标准值2.74MPa，但由于最大应力值只占据了整个拱脚应力分布的极少部分，且本文分析过程中采用的是素混凝土模型，而实际施工中拱脚处混凝土进行了配筋处理，所以从整体分析，封脚混凝土处应力满足要求。

4 结论

根据第三部分应力计算结果可以看出：两种工况下拱座混凝土的最大拉应力均未超过文献[1]的允许应力；封脚处的混凝土最大拉应力达到了6.21MPa，局部区域应力值超过了文献[1]的允许应力，但考虑实际施工工程的配筋因素以及最大拉应力值所占比极小，因此，封脚处混凝土受力也满足要求；拱座和封脚处混凝土的最大压应力较大，但均为超过允许值，拱座混凝土和封脚混凝土主要以受压为主，整个拱脚在最不利工况中受力合理。