钛合金TA7铣削加工特性研究

何绍川,李 晗,安庆龙,陈 明

(1.中国航发贵州黎阳航空动力有限公司,贵阳 550014;2.上海交通大学机械与动力工程学院,上海 200240)

0 引言

钛及钛合金具有诸多优异的物理化学性能,被广泛应用于一些重要的工程领域。相比于α相的多晶纯钛,α相钛合金由于合金元素原子的固溶强化而表现出更高的强度,TA7钛合金(Ti-5Al-2.5Sn合金)是最为常见、使用最为广泛的α钛合金之一[1-3]。由于TA7钛合金在高温下具有良好的热稳定性,抗氧化性,延展性和断裂韧性和无磁性,因此在航空、航天、舰船、低温工程等领域具有广阔前景。然而,由于其加工过程中切削温度高、加工硬化严重、变形系数小、刀具易磨损等特点,使其成为了典型的难加工材料[4-6]。

目前,对TA7钛合金的研究主要聚焦于热处理工艺、温度、拉伸载荷等参数对其微观组织和力学性能的影响。张斌等[7-8]研究了TA7钛合金拉伸和压缩时的力学行为及显微结构,结果表明TA7钛合金的力学行为表现出了显著的拉压不对称性,拉伸屈服应力和应变硬化分别低于压缩屈服应力和应变硬化。TA7钛合金的拉压不对称性在高应变率下更加显著,而温度对拉压不对称性并没有明显影响。刘志丹[9]对比分析了TA7、TB2和TC4钛合金的低温准静态拉伸行为和低温下的变形组织及断裂特征。结果表明,随温度下降,TA7、TB2和TC4合金的抗拉和屈服强度明显上升。随应变速率提高,TA7、TB2和TC4合金的室温及低温强度增高,而延伸率下降。DU等[10]通过高温单轴拉伸试验研究了TA7钛合金的拉伸行为。结果表明,在870 ℃时,最大伸长率为199.8%。880 ℃和900 ℃的TA7钛合金接缝的抗剪强度分别为568.4 MPa和569.1 MPa。LI等[11]采用电子束焊接(EBW)方法对不同类型钛合金TC4/TA7进行了焊接,并对其显微组织和焊接接头的力学性能进行了系统研究。结果表明,在不同区域焊接接头有明显差异。熔合区(FZ)主要由为α′马氏体。TC4的热影响区由马氏体、块状α相、原始α相和β相组成。TA7热影响区由少量马氏体、块状α相和原始α组成。拉伸断裂形貌主要表现为韧性断裂。SUN等[12]采用商业纯钛和金属Ti-5Al-2.5Sn钛在293 K和77 K温度下进行了对称推拉疲劳试验。通过透射电镜对其微观结构进行了研究,纯钛在77 K时比293 K时具有更高的强度和延展性,低周疲劳寿命更长。Ti-5Al-2.5Sn合金在293 K时发生循环软化。纯钛和Ti-5Al-2.5Sn钛合金的变形中均以滑移为主。在293 K循环变形时,Ti-5Al-2.5Sn合金发生滑移和孪生。

然而,目前关于TA7钛合金的铣削特性的研究鲜有报道。本文通过开展钛合金TA7铣削实验,研究切削参数对TAT切削特性的影响规律。基于MINITAB分别建立切削力、表面粗糙度与切削参数的回归模型,并分析切削力、表面粗糙度、残余应力与切削参数的响应关系。揭示切削参数对切削力时域和频域信号、已加工表面形貌与残余应力影响规律。该研究可为TA7钛合金在航空航天零部件的切削加工参数选择及其应用提供一定的理论参考。

1 材料表征与铣削实验

1.1 工件材料

工件材料为钛合金TA7,其化学成分组成如表1所示。为分析TA7的微观组织。采用腐蚀剂采用2%氢氟酸+10%硝酸+88%水,腐蚀时间为50 s。得到如图1所示的金相组织。TA7合金主要由α相组成。此外,钛合金TA7的晶体结构采用X射线衍射仪进行测定,得到了TA7钛合金的XRD衍射图谱,如图2所示。

(a) 200倍(b) 1000倍

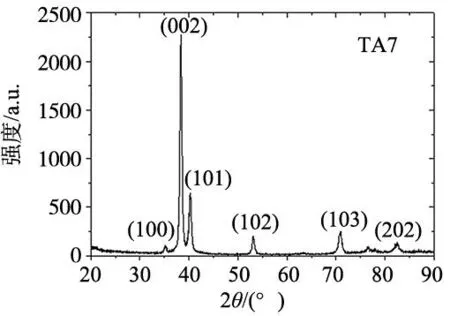
图2 钛合金TA7的XRD晶体结构

表1 TA7钛合金的化学成分

材料毛坯为不规则圆弧状,横截面尺寸为60 mm(长)×20 mm(宽)的长方形。为便于测力设备装夹,根据直线轮廓边长,采用线切割加工成两种类型的长方块,60 mm(长)×40 mm(宽)×20 mm(厚度)。TA7铣削加工采用4刃TiAlN系耐热涂层硬质合金立铣刀,刀具规格为D12*R0.5*26*L75。

1.2 铣削实验

为研究切削参数对TA7切削特性的影响。设计三因素三水平正交实验,如表2所示。其中,切削宽度为1 mm,每次走刀长度为55 mm。铣削实验在DMU70V高速加工中心进行,采用侧铣,顺铣加工,每组切削参数的每次走刀长度为55 mm,走刀4次。如图3所示。铣削过程中,采用压力传感器(Kistler 9272)和多通道电荷放大器(Kistler 5070A)以及数据采集系统对切削力分量进行在线监测。基于Kistler加速度传感器对切削过程中的振动进行检测和采集切削顺序从切削深度最大的开始,即1.5 mm,1.0 mm,到0.5 mm。铣削完成后保留每组切削参数加工面,然后离线分析每组参数的已加工表面粗糙度/形貌和残余应力分布。

图3 TA7铣削实验现场

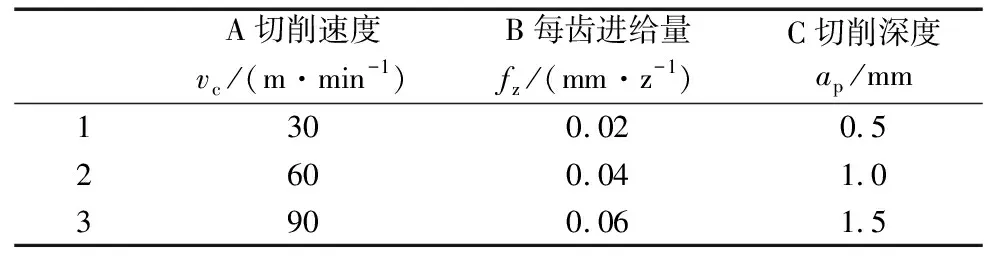
表2 三因素三水平正交实验

表3为正交实验的切削力和表面粗糙度结果。其中切削力为平均切削合力(切向力、径向力和轴向力的合力)。切削力信号为轴向分力(Fxi)、径向分力(Fyi)和切向分力(Fzi)。则平均切削合力可由式(1)确定:

表3 正交实验切削力和表面粗糙度结果

(1)

此外,已加工表面粗糙度和表面形貌采用激光共聚焦显微镜(Keyence,VK-X3000)进行检测,轮廓曲线的算术平均高度Ra的计算方法可由式(2)确定:

(2)

2 实验结果讨论与分析

2.1 切削力信号分析

为探究切削参数(vc,fz,ap)跟切削力F的关系,分析切削参数对切削力的影响,建立如下的预测模型:

(3)

对式(3)两端取对数lg,采用MINITAB软件进行回归建模,再通过转换得到:

(4)

图4是采用MINITAB软件对切削合力F与切削参数(vc,fz,ap)的响应关系进行分析。图4a是切削力F与切削速度vc、每齿进给量fz的响应曲面图和等值线图。由曲面图可知,切削力F与切削速度vc、每齿进给量fz的响应关系呈现“波峰波谷”特征,这是切削速度和进给量综合作用导致。由等值线图可知,切削力小于20 N的vc和fz组合范围是:vc=30～70 m/min,fz=0.02～0.03 mm/z。图4b是切削力F与切削深度ap、切削速度vc的响应曲面图和等值线图。由曲面图可知,切削力F与切削深度ap、切削速度vc的响应关系呈现“波峰波谷”特征。由等值线图可知,切削力小于20 N的vc和ap组合范围是:vc=30～60 m/min,ap=0.4～0.8 mm。图4c是切削力F与切削深度ap、每齿进给量fz的响应曲面图和等值线图。由曲面图可知,切削力F与切削深度ap、每齿进给量fz的响应关系呈现“波峰波谷”特征。由等值线图可知,切削力小于20 N的fz和ap组合范围是:fz=0.02～0.03 mm/z,ap=0.4～0.9 mm。

(a) vc=30～70 m/min,fz=0.02～0.03 mm/z

铣削过程可分为稳态和非稳态过程,稳态铣削时切削力信号由机床主轴转动频率SF、刀具走刀频率TPF及其倍频组成。主轴转动频率和刀具走刀频率可表示为:

(5)

式中:N是主轴转速,z是铣刀齿数。

根据式(5)、刀具和切削参数可以计算得到主轴转动频率SF和刀具走刀频率TPF:刀具直径D=12 mm,刀具齿数z=4。对于切削速度为vc=30 m/min,即主轴转速为N=796 r/min,有SF=13.27 Hz,TPF=53.08 Hz。对于切削速度为vc=60 m/min,即主轴转速为N=1592 r/min,有SF=26.54 Hz,TPF=106.16 Hz。对于切削速度为vc=90 m/min,即主轴转速为N=2388 r/min,有SF=39.81 Hz,TPF=159.24 Hz。图5和图6为正交实验切削力结果的时域和频域信号图。图5为正交实验切削合力时域信号图谱。对于切削速度为vc=30 m/min (图5a～图5c),周期T=0.07 s,选择2个周期的时域信号呈现在图中,分析发现,其有着相同变化趋势,随着进给和切深加大,力信号幅值增加(图5a～图5c对应序号1～3)。对于切削速度为vc=60 m/min(图5d～图5f),周期为T=0.035 s,选择5个周期的时域信号呈现在图中。分析发现,进给量和切削深度交互作用导致力信号差异性变化(图5d～图5f对应序号4～6)。切削速度为vc=90 m/min(图5g～图5i),周期为T=0.025 s,选择8个周期的时域信号呈现在图中。对比低速(vc=30 m/min)分析发现,切削速度提升3倍导致力信号幅值增加(图5d～图5f对应序号4～6)。

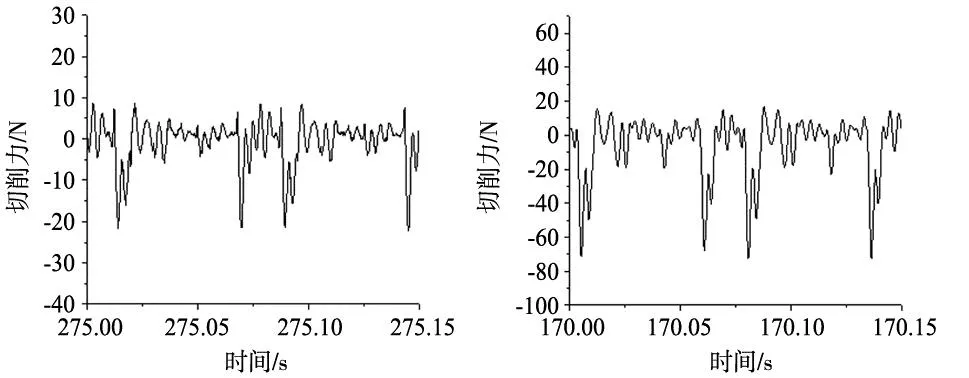
(a) 序号1 (b) 序号2

(a) 序号1 (b) 序号2

2.2 切削振动信号分析

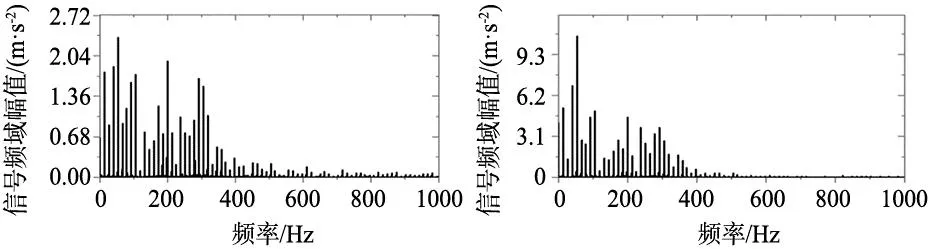
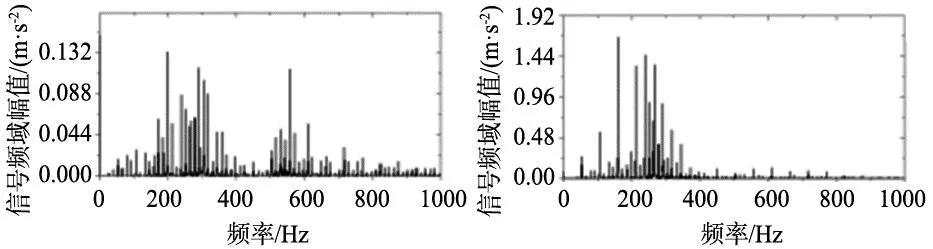
正交实验过程中,基于加速度传感器采集了沿刀具进给速度(X)和切削速度(Y)方向的振动信号幅值随时间变化。此外,基于傅里叶变换(FFT)得到了切削振动频域信号的幅值随频率的变化。图7～图10是沿刀具进给速度(X)和切削速度(Y)方向的振动信号的时域和频域信号图谱。由图可知,对于切削速度为vc=30 m/min(图7a～图7c),分析发现,其有着相同变化趋势,随着进给和切深加大,振动信号幅值增加(图7a～图7c对应序号1～3)。对于切削速度为vc=60 m/min(图7d～图7f),分析发现,进给量和切削深度交互作用导致力信号差异性变化(图7d～图7f对应序号4～6)。切削速度为vc=90 m/min(图7g～图7i),对比低速(vc=30 m/min)分析发现,切削速度提升导致振动幅值增加,同时进给量和切削深度交互作用导致振动信号差异性变化(图7d～图7f对应序号4～6)。此外,相同条件下,沿进给速度方向的切削振动较切削速度方向剧烈。

(a) 序号1 (b) 序号2

(a) 序号1 (b) 序号2

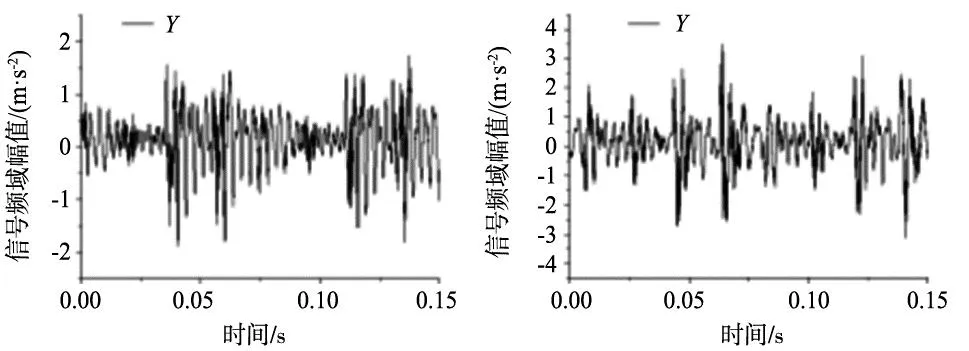
(a) 序号1 (b) 序号2

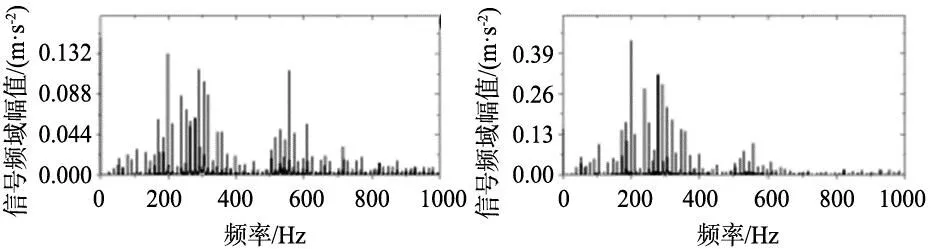
(a) 序号1 (b) 序号2

2.3 已加工表面形貌与残余应力分析

为探究切削参数(vc,fz,ap)与表面粗糙度Ra的关系,建立如下的预测模型:

(6)

对式(6)两端取对数lg,采用MINITAB软件进行线性回归建模,得到回归方程,然后通过转换得到:

(7)

图11是采用MINITAB对表面粗糙度Ra和切削参数(vc,fz,ap)的响应关系进行分析:图11a是表面粗糙度Ra与切削速度vc、每齿进给量fz的响应曲面图和等值线图。由曲面图可知,表面粗糙度Ra与切削速度vc、每齿进给量fz的响应关系呈现“波峰波谷”特征。由等值线图可知,表面粗糙度Ra小于0.3 μm的vc和fz组合范围是vc=40～50 m/min,fz=0.02～0.03 mm/z。图11b是表面粗糙度Ra与切削深度ap、切削速度vc的响应曲面图和等值线图。由曲面图可知,表面粗糙度Ra与切削深度ap、切削速度vc的响应关系呈现“波峰波谷”特征。由等值线图可知,表面粗糙度Ra小于0.3 μm的vc和ap组合范围是vc=40～60 m/min,ap=0.4～0.7 mm。图11c是表面粗糙度Ra与切削深度ap、每齿进给量fz的响应曲面图和等值线图。由曲面图可知,表面粗糙度Ra与切削深度ap、每齿进给量fz的响应关系呈现“递增”特征,是切削深度和每齿进给量综合作用导致。由等值线图可知,表面粗糙度Ra小于0.3 μm的fz和ap组合范围是fz=0.02～0.05 mm/z,ap=0.4～0.7 mm。

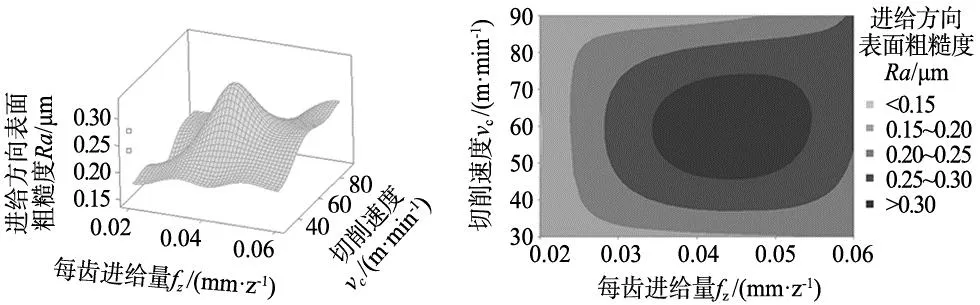
(a) vc=40～50 m/min,fz=0.02～0.03 mm/z

图12～图14是采用激光共聚焦显微镜测量得到的正交实验已加工表面二维、三维及剖面轮廓图。由图可知,在已加工表面出现明显划痕,这是刀具的进给纹路,根据前文的表面粗糙度的正交实验分析,随着每齿进给量的增加,表面粗糙度值增大,划痕明显。

(a) 序号1 (b) 序号2 (c) 序号3

(a) 序号1 (b) 序号2 (c) 序号3

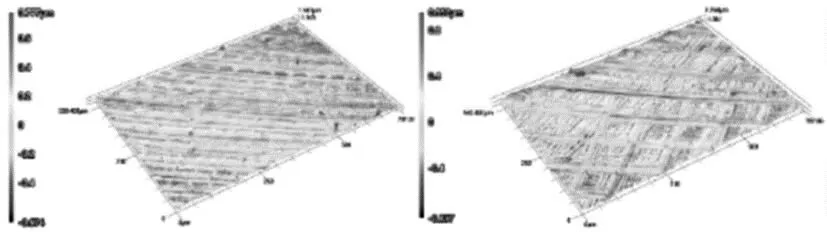
(a) 序号1(b) 序号2

工件已加工表面的残余应力(切削速度方向和进给速度方向)采用μ-X360s残余应力分析仪进行测量。图15是正交实验的沿切削速度和进给速度方向的残余应力。由图可知,切削速度和进给速度方向的残余应力与切削参数的变化呈现各向异性变化。残余应力各向异性变化可归结于机械载荷和热载荷交替主导作用。通常来说,热载荷占主导效应导致拉应力增加,机械挤压占主导作用则导致压应力增加。

图15 正交实验已加工表面残余应力分析

3 结论

通过设计三因素三水平正交实验,研究了不同切削参数下的红色涂层刀具铣削加工TA7的切削力和振动信号、已加工表面形貌、残余应力。基于MINITAB分别建立了切削力、表面粗糙度与切削参数的回归模型,并分析了切削力、表面粗糙度、残余应力与切削参数的响应关系。主要结论如下:

(1)基于MINITAB的切削力方差分析及傅里叶变换的切削力频域研究。采用MINITAB单因素方差分析了切削速度、每齿进给量和切削深度对切削合力的影响,得到了切削参数对切削合力的影响主效应和交互作用规律。

(2)基于激光共聚焦显微镜的已加工表面形貌和粗糙度分析。采用MINITAB单因素方差分析了切削速度、每齿进给量和切削深度对表面粗糙度的影响,通过线性回归建模,得到了回归方程。获得了表面粗糙度和切削参数的响应关系。结果表明表面粗糙度随切削速度的增加有减小趋势,随每齿进给量和切削深度的增加呈现增大趋势。

(3)不同切削参数下的切削速度和进给速度方向的残余应力研究。采用残余应力分析仪测量了已加工表面的切削速度和进给速度方向残余应力。结果表明切削速度和进给速度方向的残余应力与切削参数的变化呈现各向异性变化。残余应力各项异性变化可归结于机械载荷和热载荷交替主导作用。热载荷占主导效应导致拉应力增加,机械挤压占主导作用则导致压应力增加。