基于激光陀螺测角仪的角度计量动态特性分析*

季岚青,黄 垚,朱维斌,邹 伟

(1.中国计量大学计量测试工程学院,杭州 310018;2.中国计量科学研究院几何量所,北京 100029)

0 引言

传统角度测量时的工作面向的测量仪器及传感器普遍用于稳定环境,静态输入条件下的测量工作,对动态测量特性不敏感;新一代角度测量面向航空、航天、高端制造领域,其中的测量仪器及传感器普遍用于运动过程中实时变化被测对象的状态监测,要求全过程实时测量结果的准确、可靠,因此开展动态角度测量的研究具有十分重要的意义。

目前,动态角度测量技术是角度测量方面的重要内容之一,国内外学者对于动态角度测量技术进行了大量试验和研究,刘西钊等[1]创造出角定位重复性为0.022″的动态光电自准直仪,自此开辟了国内动态自准直仪创新的先河。沈忙作[2]研制出以四象限探测器作为检测元件的二维动态光电自准直仪。当投射到被测物体反射镜上的光反射回来时,会在四象限探测器上成像,当被测反射镜发生角度变化时,会引起像斑在探测器上发生位置变化。该系统实现了在二维测角范围±250″内具有非常好的输出线性度且测量出的最大误差不超过5″。朱小平[3]研制出应用了PSD器件的双轴自准直仪,该系统在测角范围±60″内,测角误差小于0.5″,在-270″～190″,测角误差不超过1″。ZHANG等[4]通过改善迈克尔逊干涉仪的光路结构,将迈克尔逊干涉仪中的两个平面反射镜用定值角来代替,设计出拥有双定值角的干涉仪测角系统,可在0°～360°的范围内可以实现任意角度的高精度测量,并且测量不确定度小于0.3″。但该方法定值角的加工难度较大,系统过于复杂不利于实际应用。

为了实现角度的动态测量,中国计量科学研究院研制出一种基于环形激光原的激光陀螺测角仪,它具有优良的性能如高精度,高分辨率,高灵敏度[5-6],除此之外还具有优良的动态特性。激光陀螺测角仪作为一种新型的接触式角度测量仪器,为了满足全圆角动态测量结果的准确性与可靠性,因此需要对激光陀螺测角仪进行动态特性的研究与分析[9-11],这也是激光陀螺测角仪能够进行动态角度测量的前提与依据。动态特性是测量系统在动态工作中所呈现的特性,它决定测量系统快变参数的精度,描述在动态测量过程中测量系统中输出量和输入量之间的关系。测量系统的动态特性一般包括脉冲响应、阶跃响应、幅频响应、相频响应、谐波失真度[8]。本文主要研究的是激光陀螺测角仪在不同动态特性情况下对角度误差的影响,以及激光陀螺测角仪的动态特性的测量方法。

1 动态特性的组成与测量方法

1.1 动态特性的组成

1.1.1 脉冲响应

脉冲响应表示的是动态测量系统对外部变化的反应,即代表着当测量系统受到外部环境的冲击时,系统能够达到稳定状态的时间函数。脉冲响应也包含了所有得频率,表现为系统对所有频率得响应。

1.1.2 阶跃响应

阶跃响应是指系统在单位阶跃信号的作用下所产生的零状态响应。因为其能很大程度上反应系统的动态特性,所以是分析系统时十分重要和常用的响应类型,常常用来评判系统的动态性能。激光陀螺测角仪作为一个二阶系统,所以分析其输入、输出信号的阻尼比ζ和自然频率ωn[12]对激光陀螺测角仪的动态性能的评定具有十分重要的意义。

1.1.3 幅频响应

幅频响应代表的是测量系统的不同频率下输出信号的大小变化与频率之间的关系,即评价在动态测量中测量系统所能达到最佳状态的转速。动态角测量精度受限于测量转速。

1.1.4 相频响应

相频响应代表的是不同频率下测量系统输入信号与输出信号的相位偏移问题,即评价测量系统在不同频率下信号的延迟时间。

1.1.5 谐波失真度

谐波失真度是动态角度计量中的一个重要特性,它是由非线性元器件引起的,当信号通过非线性元器件时,输出信号比输入信号多出的额外的谐波部分。即谐波失真是因为系统不是完全线性造成的。

1.2 测量方法和原理

1.2.1 同步测量原理

为了保证动态特性的数据同步采集,自研制出同步触发装置,如图1所示,首先通过转台输出四路光栅信号,经细分模块后送至同步触发板(DASA);DASA模块内完成采集的光栅信号等分平均算法后得到光栅角度测量值,然后同时触发光栅测量和激光陀螺测角仪测量通道;光栅角度测量值经过串口上传到上位机接收;激光陀螺测角仪角度测量值通过其配套的计数装置发送至上位机接收。

图1 动态角度同步采集系统示意图

在整个动态角度同步采集的过程中,核心环节为光栅角度测量值和陀螺仪角度测量值的同步获取,二者数据同步采集方案如图2所示。

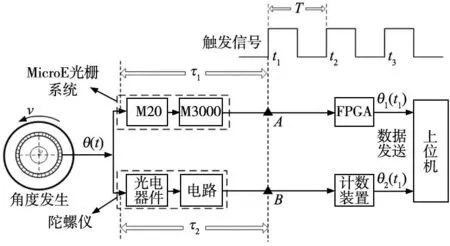
图2 数据同步采集方案

在动态角度采集过程中,获取到的角度值均是与时间相关的量。假设光栅系统的延时时间为τ1;陀螺仪的延时时间为τ2。DASA产生具有固定时间间隔T的触发信号,当触发信号到来的t1时刻,光栅输出的角度值θ1(t1)经FPGA上传至上位机接收;同时陀螺仪输出的角度值θ2(t1)经计数装置上传至上位机接收。

1.2.2 三参数正弦逼近法

转台在进行频率一定的正弦运动时,激光陀螺测角仪和激光干涉仪输出的数据是一条正弦曲线,设被采样的正弦信号为[7]:

Y(t)=A0sin(w0+θ0)+C0

(1)

式中:A0为采样信号的理想幅值,w0为理想信号的信号频率,θ0为采样信号的理想相位,C0为信号理想直流偏移。对于任意的正弦信号,都可以用这4个参数表示,为了使其便于拟合计算,对式(1)进行展开,如式(2)所示。

Y(t)=Acos(w0t)+Bsin(w0t)+C

(2)

式中:A=A0sin(θ0),B=B0cos(θ0),C=C0。

设正弦信号在tk(k=0,1,2,3,…)时的采样值为Y(tk),如式(3)所示。

Y(tk)=Acos(w0tk)+Bsin(w0tk)+C

(3)

某一时刻的采样估计值与采样真实值的误差平方为:

(4)

式中:N为采样长度。令:

(5)

(6)

式(4)的正弦信号3参数的最小二乘解如式(7)所示。

X=(DTD)-1(DTY)

(7)

根据式(8),可以得到采样信号的幅值与相位分别是:

(8)

根据式(4)～式(7),进一步求出标准信号的幅值和相位分别是:

(9)

1.3 谐波失真度计算方法

谐波失真度是动态角度计量中的一个重要特性,它是由非线性元器件引起的,当信号通过非线性元器件时,输出信号比输入信号多出的额外的谐波部分。即谐波失真是因为系统不是完全线性造成的。由于转台在做正弦运动,激光陀螺测角仪输出的是周期性信号,因此将采集信号Y(tk)(k=0,1,2,3,…)通过傅里叶变换分解为直流信号C和不同频率的正弦信号的线性叠加:

(10)

式中:Cm表示第m次谐波的幅值,mw为角频率,φm为初始相位,ω/2π为基波分量的频率,n为采样点数,当n为偶数时,可以计算的最高阶次o为n/2,当n为奇数时,可以计算的最高阶次o为(n-1)/2。

因此谐波失真度的计算表达式为:

(11)

2 实验分析

在角位置动态特性的实验过程中实验环境没有强磁场的存在(强磁场的环境下激光陀螺测角仪的测角精度会大大降低),没有明显的气流扰动,整个实验过程均在隔振平台或隔振地基上完成,环境温度20±0.5 ℃,湿度50±10%RH。

2.1 阶跃响应特性

为了评价激光陀螺测角仪的稳定性,从而展开对激光陀螺测角仪的阶跃响应特性的研究。利用转台模拟出阶跃响应,并通过同步触发板对激光陀螺测角仪进行阶跃响应特性进行实验研究,测量系统的安装示意图和实物图分布如图3和图4所示。

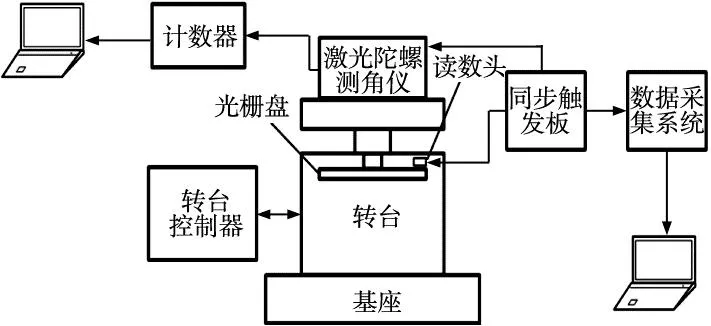
图3 测量系统的安装示意图

图4 测量系统的实物图

图4中1是激光陀螺测角仪,2是转台,3是读数头,4是计数器,5是同步触发板。

将激光陀螺测角仪置于转台上,并用胶枪将其与转台旋转面固定在一起。利用同步触发板采集转台90°相隔的4个读数头的数据,读数头的排列方式如图5所示。

这4组读数头的数据等分平均后的结果作为转台的反馈信号。设计同步触发板的触发信号为2 kHz,当同步触发板开始触发时,控制转台以加速度1500 (°)/s2,速度299 (°)/s分别从静止运动到10″。比较激光陀螺测角仪和四读数头等分平均后两者之间的角度输出,如图6所示。两者之间的角位置偏差如图7所示。

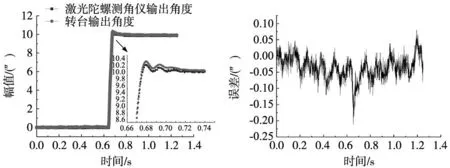
图6 阶跃响应时转台与激光陀螺角位置输出

由图6和图7可知,四读数头角位置平均值和激光陀螺测角仪的角度输出,在10″幅值的阶跃响应实验中最大角位置偏差为0.2″,且两者角位置变化曲线趋势保持一致且利用MATLAB对两者的阶跃数值进行拟合得到,激光陀螺测角仪的阻尼比ζG=0.707,自然频率wNg=67.79;转台的阻尼比ζT=0.703,自然频率wNT=67.81。

由于转台和激光陀螺测角仪两者同步输出,他们的输出频率一致为2 kHz,即每两个数据之间相隔0.000 5 s,则转台和激光陀螺测角仪的速率偏差如图8所示。

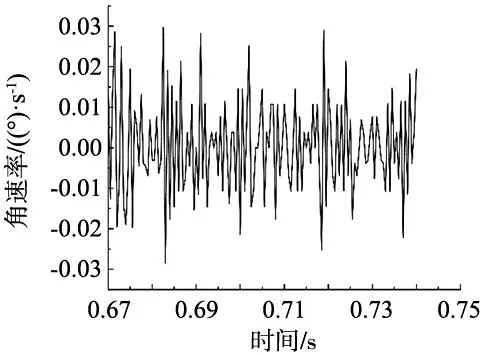
图8 跃响应时转台与激光陀螺测角仪角速率偏差

如图8所示,根据式(12)可以得到幅值为10″时,转台和激光陀螺测角仪之间角速率偏差的重复性为0.012 (°)/s。

(12)

式中:Kn表示第n次测量的刻度系数K,m表示重复测量的次数。

根据上述阶跃响应实验,可以明显的看出来在转台模拟阶跃响应时通过激光陀螺测角仪测量得到的角位置变化曲线与转台四读数头等分平均得到的角位置变化曲线,其变化趋势基本相同且计算出来的两者角位置偏差以及角速率偏重复性均没有较大差别。具体数据如表1所示。

表1 不同阶跃幅值下两者之间的角位置偏差、角速率偏差值、阻尼比和自然频率

综上所述,激光陀螺测角仪的阶跃响应特性与发生装置的阶跃特性相比角位置偏差和角速率偏差重复性均没有较大差别,且阻尼比为最佳阻尼比,意味着激光陀螺测角仪能够快速进入稳定状态。

2.2 脉冲响应特性

为了进一步检测激光陀螺测角仪的稳定性、时变特性、敏感性,我们使用脉冲响应来观察其特性。为了使转台模拟出脉冲响应,给予转台加速度1500 (°)/s2,速度299 (°)/s,幅值30″,实验装置如图4所示。仍然以等间隔的4个读数头的平均值作为转台角位置的反馈值。并以此作为测量真值来观察激光陀螺测角仪的脉冲响应特性,如图9所示。

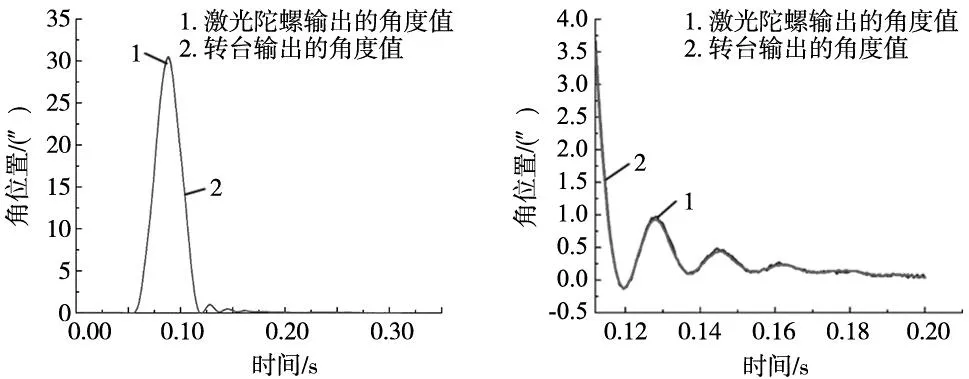
(a) 转台与激光陀螺脉冲响应输出对比图 (b) 转台与激光陀螺测角仪脉冲响应局部图

由图9可以清楚地看见,当转台发生脉冲响应时,激光陀螺测角仪输出的角度变化趋势与转台输出的角度变化趋势基本一致,其他们之间的角位置偏差和角速率偏差如图10和图11所示。

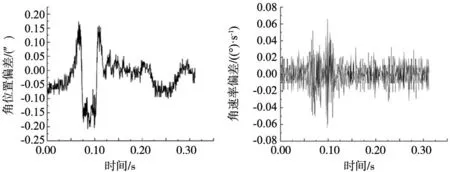
图10 转台与激光陀螺测角仪输出的角位置偏差

根据图10和图11可以明显的看出在转台发生脉冲响应时,转台与激光陀螺测角仪输出的角位置偏差为0.2″,角速率偏差为0.06 (°)/s。

由于角度变化趋势,角位置偏差,角速率偏差没有明显差异,为了进一步观察两者之间脉冲响应的变化,对转台与激光陀螺测角仪输出的脉冲曲线进行傅里叶变换分析其周期性成分分布情况差异,如图12所示。

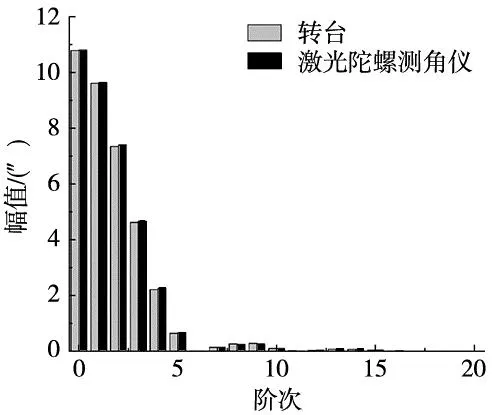
图12 转台与激光陀螺测角仪输出角度的频谱图

从图12可以看出,以转台输出的脉冲响应各阶次的谐波幅值,幅值主要分布在1阶、2阶、3阶、4阶、5阶、8阶、9阶。转台作为发生装置,激光陀螺测角仪感应到的脉冲响应变化的各阶次幅值与转台的谐波幅值极为接近,为动态角度测量提供了依据。

2.3 幅频响应、相频响应和谐波失真度

为了验证激光陀螺测角仪在不同频率下的幅值响应特性与相频响应特性,我们需要使转台作正弦运动。并且为了更好的验证激光陀螺测角仪作正弦运动时的幅值与相位,我们使用Renishaw的激光干涉仪作为标准器件,参数如表2所示。实验过程中,我们将激光陀螺测角仪置于振动台上,利用同步触发板同时给予激光陀螺测角仪与激光干涉仪脉冲信号。实验平台示意图如图13所示。实验平台实物图如图14所示。

表2 Renishaw激光干涉仪的参数

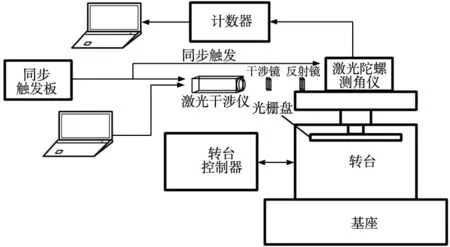
图13 实验平台示意图

1.激光干涉仪 2.干涉镜 3.反射镜 4.激光陀螺测角仪

为了更好地研究激光陀螺测角仪的幅频响应和相频响应特性,在实验中分别给予转台3 Hz、5 Hz、7 Hz的振动频率,观察激光陀螺测角仪与激光干涉仪产生的角度变化曲线,和角位置偏差曲线,3 Hz频率下激光陀螺测角仪与激光干涉仪输出的角度图如图15和图16所示。

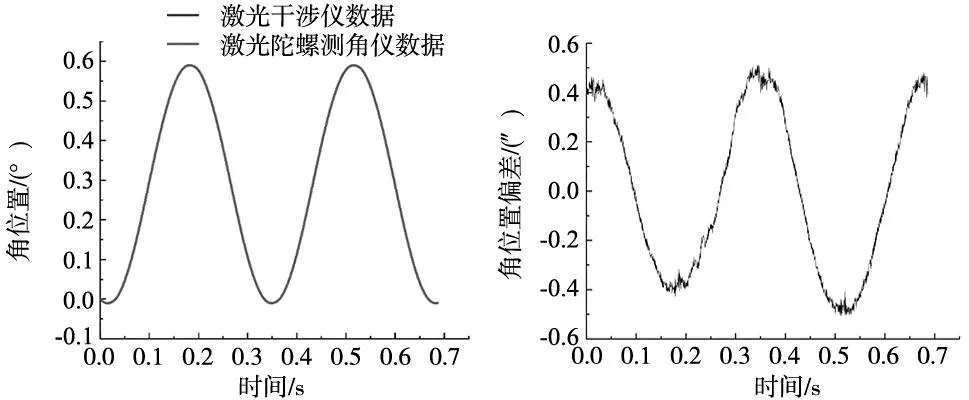
图15 3 Hz频率下两者输出的角度值的变化曲线

从图中可以明显的看出当转台产生3 Hz的振动频率时,在同步触发板的作用下,激光陀螺测角仪输出的角度值与激光干涉仪输出的角度值两者之间的最大误差为0.52″且两者之间的变化趋势基本一直。通过三参数拟合法可以得出激光陀螺测角仪测出的正弦曲线幅值为0.303 5°,相位为-107.145 4°,激光干涉仪测出的幅值为0.303 4°,相位为-107.145 8°。所以,当转台产生3 Hz的振动频率时,激光陀螺测角仪的幅值相对于激光干涉仪的幅值变化率为0.032%,相位变化为0.000 4°。

根据式(11),可以分别得到激光陀螺测角仪与激光干涉仪的谐波失真度为0.731 4%、0.730 2%。

当转台以5 Hz、7 Hz的频率分别振动时,激光陀螺测角仪与激光干涉仪产生的角度值如图17所示,两者之间的角位置偏差如图18所示。

(a) 5 Hz频率下两者输出的角度值 (b) 7 Hz频率下两者输出的角度值

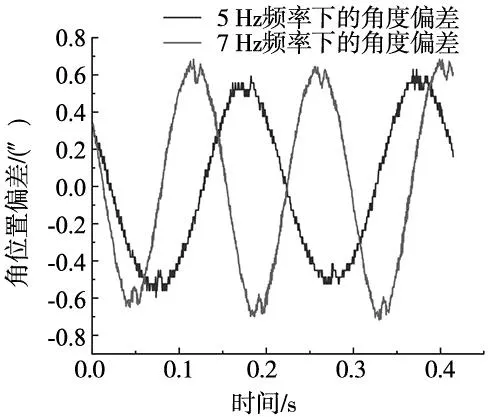
图18 不同频率下两者输出的角度偏差值

可以明显的看出转台在产生5 Hz、7 Hz的正弦振动时,激光陀螺测角仪与激光干涉仪输出的角度曲线变化趋势基本一直,两者之间的产生的角位置误差分别为0.55″、0.62″。因此不同频率下激光陀螺测角仪与激光干涉仪产生的角位置偏差差距不大。从幅值和相位上看,不同频率下激光干涉仪产生的幅值为0.302 5°、0.301 9°;相位为-44.585 3°、122.912 4°;谐波失真度为0.491 7%、0.392 7%。激光陀螺测角仪产生的幅值为0.302 6°、0.302 0°;相位为-44.585 4°、122.912 2°;谐波失真度为0.492 1%、0.391 4%。具体变化如表3所示。

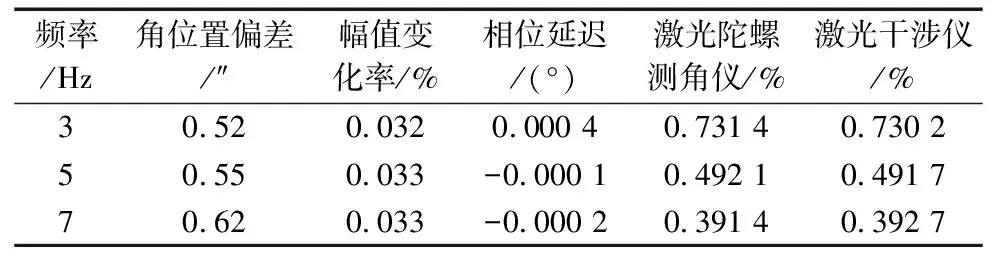
表3 激光陀螺测角仪的幅频响应、相频响应和谐波失真度

由表3可以明显的看出激光陀螺测角仪具有良好幅频响应和相频响应特性,在不同频率的测试下激光陀螺测角仪的幅值变化极小且幅值变化率基本不变。从相位延迟量来看,相位延迟都保持在10-4°的量级。

3 结束语

本文首先通过同步触发板将转台与激光陀螺测角仪进行同步触发并进行数据采集,通过转台模拟脉冲响应与阶跃响应,比较转台四读数头输出的角度平均值与激光陀螺测角仪角度值作比较,分析两者的阻尼比和频谱幅值,证明了激光陀螺测角仪具有优良的脉冲响应与阶跃响应,然后将激光陀螺测角仪与激光干涉仪进行同步触发,实验结果表明了不同频率下两者之间的幅值变化率基本不变,相位延迟基本可以忽略不计且与激光干涉仪相比,激光陀螺测角仪的动态角位置误差在0.6″左右。进一步证明了激光陀螺测角仪具有优良的动态特性,为全圆动态角度测量结果的可靠性提供了依据。