激光雷达与惯性测量单元同步融合下的园区三维建图

马庆禄， 汪军豪， 张 杰， 邹 政

（1. 重庆交通大学 交通运输学院， 重庆 400074；2. 同济大学 道路与交通工程教育部重点实验室， 上海 201804）

1 引 言

随着自动驾驶技术的不断发展，同步定位与建图（Simultaneous Localization and Mapping，SLAM）技术逐步成熟。SLAM 技术是指通过车辆在未知环境中动态构建的空间特征从而进行自身位姿估计，实现同步定位和增量式建图的目标。

随着一个在未知位置和未知环境中移动的机器人能否在建立环境地图的同时确定他自身的位置的问题被提出，SLAM 技术不断发展，已经从单传感器发展为多传感器SLAM。SLAM技术应用的传感器主要包括激光雷达与视觉传感器［1］。陈龙等［2］通过对比激光雷达SLAM 与视觉SLAM 的定位建图效果，发现激光SLAM 比视觉SLAM 更具备稳定性。有研究发现惯性测量单元（Inertial Measurement Unit， IMU）与3D激光雷达有很好的互补性［3］。Ji 等［4］提出的LOAM 算法框架通过低频高精的后端与高频低精的前端来提升SLAM 效能，但LOAM 算法无法使用IMU 进行整个系统的优化。Gilmar 等［5］将LOAM 算法进行改进，提出了适用性更好的EKF-SAM 算法，但它无法进行回环检测，也无法融入绝对测量数据进行位姿校正，而且LOAM存在大场景测试中偏移的问题。Michael 等［6］提出了激光雷达与IMU 融合的Fast-SLAM 2.0 算法，该方法增强了设备位于不平坦区域的建图能力。黄粒等［7］通过改进后端优化提高计算效率，取得了较低的轨迹误差、绝对轨迹误差和相对位姿误差，提高了同步定位与建图的精度。杨智宇等［8］利用因子图联合优化共同提高位姿估计精度。王挺等［9］运用GR-LOAM 算法，通过激光雷达和IMU 等多传感器融合来提高建图效果，由于传感器本身存在精度误差，多传感器融合容易导致累计误差的产生。尹芳等［10］针对模型未知的空间非合作旋转目标的模型重建和位姿估计问题，利用激光雷达采集的3D 点云，提出一种基于位姿图优化的SLAM 技术框架，以解决跟踪过程中产生的累积误差问题。杨林等［11］提出了一种基于激光惯性的融合SLAM 算法，实现了移动机器人全局一致的同步定位与地图构建。针对激光雷达与IMU 融合，一些改进SLAM 算法，如Fast-LIO［12］与Fast-LIO2［13］被提出。徐伟等［14］通过评估Fast-LIO2 算法以及其数据结构iKDtree，体现Fast-LIO2 算法的优越性。Fast-LIO2在Fast-LIO 的基础上在前端采用增量KD-tree（iKD-tree），后端采用迭代误差状态Kalman Filter，但iKD-tree 是一个静态数据结构，当需要频繁进行数据集更新时，需要重新构建整个iKDtree，算法运行效率会降低。高翔等［15］在Fast-LIO2 的基础上进行改进，用增量体素（ivoxel）取代iKD-tree，实现了同等的定位和建图精度，并取得了更快的运行速度。马艾强等［16］提出了一种面向煤矿巷道环境的激光雷达与IMU 融合的实时定位与建图方法。徐晓苏等［17］提出了一种面向室外环境的基于快速回环检测的SLAM 算法，提升了回环检测的精度与速度。陈志强等［18］提出了一个完整的激光雷达SLAM 框架SCLSLAM，将回环检测模块与扫描邻近帧集成到紧密耦合的激光雷达惯性里程计FAST-LIO2 中。目前，有些优秀算法缺少后端优化与回环检测。如果没有回环检测来修正轨迹估计中的误差，SLAM 算法的轨迹会使机器人的位姿估计逐渐偏离真实轨迹，导致SLAM 系统的性能逐渐下降，甚至无法有效地完成定位和建图任务。

激光SLAM 与IMU 在同步定位与构图导航应用方面各有优势，有着较为良好的互补性，但同时定位与建图的误差问题始终存在，部分算法缺少后端优化与回环检测，导致算法存在全局一致性较弱或者累计误差过大的问题。本文提出一种改进的激光雷达与IMU 融合SLAM 方法用以提高位姿估计精度和地图构建精度。

2 激光雷达IMU 融合的建图系统分析

2.1 SLAM 模型分析

SLAM 数学模型可以使用贝叶斯滤波理论来描述［19］。激光雷达的测量模型为距离-方位角-俯仰角模型（即距离-方位角-俯仰角模型），如式（1）所示：

其中：(x，y，z，α，ω)表示机器人位姿，(lx，ly，lz)表示地标点位置，α表示测量的地标点相对于机器人的方位角，ω表示激光雷达测量的地标点相对于机器人的俯仰角。该测量模型是一种非线性模型，需要通过优化算法来估计机器人位姿和地标点的位置。

IMU 用于测量当前时刻的角速度和加速度值。IMU 加速度计模型及陀螺仪模型如式（2）表示：

其中：ba和bω表示加速度计和陀螺仪的偏置向量，表示从物体坐标系到IMU 安装坐标系的旋转矩阵，na和nω表示加速度计和陀螺仪的随机噪声向量。

2.2 Fast-LIO2 算法

Fast-LIO2 以高效紧耦合的迭代卡尔曼滤波器（Extended Kalman Filter， EKF）为基础，将原始点云配准在地图中，利用环境中的细微特征提高数据的准确性，通过增量数据结构iKDtree 来维护地图。对于状态转移模型而言，以第一帧IMU 帧作为系统初始化输入，其初始化全局坐标系为G，并且以TL=(RL，PL)代表激光雷达和IMU 之间的外参，其运动学方程如公式（3）所示：

其中：PI和RI分别表示IMU 在全局坐标系下的位置和姿态，na和nω分别表示测量值am和ωm中的噪声；nba和ba表示am中的零偏，bω和nbw表示ωm的零偏，其离散方程为：

其中：x表示状态，u表示输入，w表示噪声。利用反向传播修正扫描帧的运动，见式（5）所示：

其中：k表示激光雷达扫描帧中的索引；pj表示第k个扫描帧在激光雷达局部坐标系以及扫描帧结束时间的采样点，每个测量点pj都包含了nj的距离和方向；剔除噪声后即是激光雷达局部坐标系中真正的点；TLk表示相应的激光雷达姿态，TL表示外参；表示对应平面的法向量；qj表示该平面的一个点。

基于上述的状态转移模型和观测模型，使用迭代卡尔曼滤波。当IMU 数据到来时则前向传播，过程噪声wi=0，前向传播状态和协方差如下：

3 改进的激光雷达IMU 融合建图算法

3.1 Fast-LIO2 算法的后端优化

对Fast-LIO2 算法引入GTSAM 后端图优化，增强激光雷达与IMU 的融合精度以提高SLAM 构图的全局一致性。GTSAM 为解决SLAM 中出现的非线性优化问题提供了一个框架，其优化过程为调用因子图以及相应图节点的值，计算因子（观测约束）的残差，因子对相关图节点的雅可比矩阵，完成迭代优化，以提高自动驾驶车辆的定位精度和稳定性。改进算法的因子图结构如图1 所示。

在GTSAM 中，IMU 预积分因子是一种重要的优化因子，车辆在t+Δt时刻的速度vt+Δt、位置pt+Δt和旋转Rt+Δt的计算公式如下：

IMU 预积分提供IMU 预积分因子，建立IMU 预积分因子首先建立IMU 模型，如式（11）所示：

其中：ωb表示IMU 坐标系中角速度的真实值，aw表示加速度真实值，bg，ba表示IMU 偏置，ng，na表示测量值的噪声，p表示位置，v表示速度，q表示姿态。根据积分关系，得到迭代公式：

根据i时刻的位置pwbi，速度以及姿态qwbi进行积分得到j时刻以及qwbj。定义预积分量并且移项整理，构建残差并离散化，根据EKF 进行泰勒展开可得：

其中：F，G分别表示方程f(xk-1，uk-1)在x̂k-1处噪声项为0 处的雅可比矩阵。预积分量的协方差矩阵可以通过F，G雅可比矩阵进行传播。

激光里程因子是一种基于激光数据的因子，对于特征点云与其对应的边缘或平面特征之间的距离为：

使用主成分分析（Pricipal Component Analysis， PCA）提取点、线和平面特征。定义几何特征的局部线性度σ1D、平面度σ2D和曲率σc分别为：

其中：Tt和Tt+k分别表示车辆在时间步t和t+k时的位姿变换矩阵，Xi表示地图上的点。

基于稀疏体素的近邻结构（incremental Voxels， iVox）与LIO 算法更加匹配［15］，而iVox 中伪希尔伯特空间曲线（Pseudo-Hilbert Curve，PHC）在降低点云配准耗时的同时不影响SLAM的精度表现。因此，通过给iVox 局部地图添加最近最少使用缓存（Least Recently Used， LRU），以克服遍历整个iVox 带来的时效问题。通过调整iVox 局部地图的容量阈值，并在添加新地图数据时筛选出使用频率较小的体素以移除，以降低iVox 遍历的复杂度。

3.2 SLAM 算法评价指标

视觉里程计（Estimation， Validation， and Optimization， EVO）评价工具是众多学者广泛认可的SLAM 系统性能评价工具［20］，主要评价参数为绝对位姿误差（Absolute Pose Error， APE）与相对位姿误差（Relative Pose Error， RPE）。APE 可以直观地反映SLAM 算法精度和轨迹的全局一致性。如下：

其中：V表示位姿对之间的相对平移向量，N表示位姿个数，Tt，i和Te，i分别表示真实轨迹和SLAM 系统估计出的轨迹，Eg，i表示为误差求解出不包含位姿旋转角的APE 参数，如下：

其中trans 表示变量平移部分。RPE 反映SLAM算法的局部精度，计算相隔Δt时间的两帧之间位姿之差，代表相应轨迹段的相对误差，如下：

其中：EAP误差的均方根误差（Root Mean Squared Error， RMSE）、误差均值（EMean）、最大误差（EMax）以及最小误差（EMin）用于评价预测值与真实值之间的差异，分别为：

此外有学者提出众多类似于点云在距离真值一定距离处的点的累积百分比或离散程度来评价点云建图性能［4］。

4 实验及结果分析

4.1 激光雷达IMU 融合建图

实验平台为Apollo D-KIT-lite 自动驾驶开发套件，采用的开发套件以及建图算法框架如图2 所示。实验场地选取为学校园区第一教学楼外。改进算法建图过程与生成点云地图的部分细节如图3 所示。改进后生成的总体地图效果优异。同一数据集分别采用原始算法与改进算法进行建图，生成的点云地图与地图细节对比如图4 所示。

图2 激光雷达IMU 融合建图实验平台与系统框架Fig.2 Experimental platform and system framework for mapping based on fusion of lidar and IMU

图3 改进算法的建图过程与效果Fig.3 Improved algorithm building process and renderings

图4 Fast-LIO2 改进前后的建图对比Fig.4 Comparison of rendering before and after improvement of Fast-LIO2

对比图4（a）与图4（b）可以明显看出，改进算法的整体建图效果优于原算法。如图4（c）所示，原算法点云重叠导致地图边缘点云厚度异常，改进算法的轮廓纤细清晰，如图4（d）所示。在地面点云上，图4（e）出现点云运动畸变，图4（f）地面平整。

EVO 对SLAM 效果进行对比，如图5 所示（彩图见期刊电子版）。数据集中的GPS 定位信息为时间戳经纬度高程信息，需要通过解算与对齐（所有传感器数据通过相应的TF 变化到同一坐标系）后才能用于地面真值作为后续SLAM 算法位姿估计的基准。图5（b）、图5（c）与图5（d）中虚线为GPS 差分得到的真实轨迹参考、蓝色为改进前Fast-LIO2 算法、绿色与红色为改进后算法（其中绿色未将回环检测因子加入图优化、红色为加入回环检测），可以发现改进算法与原算法相比，无论是否增加回环检测，改进算法的轨迹估计更接近GPS 提供的轨迹真值。

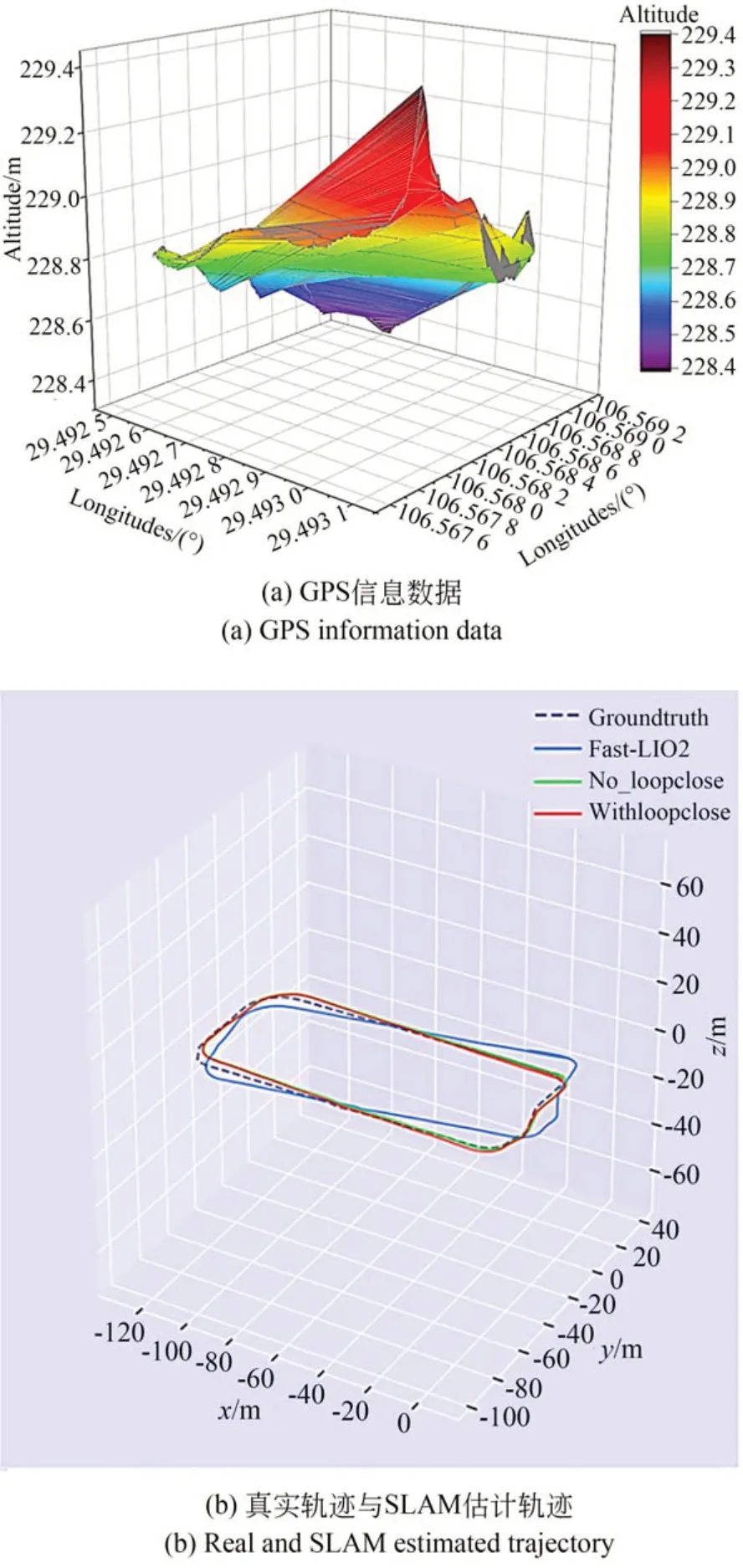
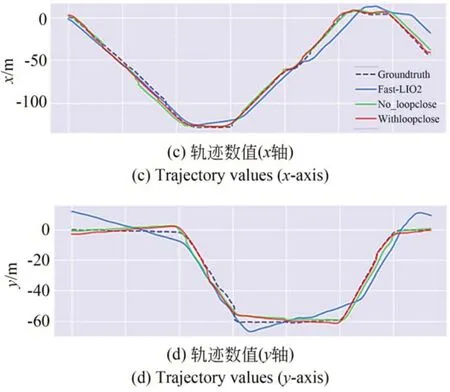
图5 SLAM 位姿估计Fig.5 SLAM pose estimation

4.2 实验评价分析

通过APE 与RPE 对改进前后的融合算法进行对比分析，结果如图6 所示。

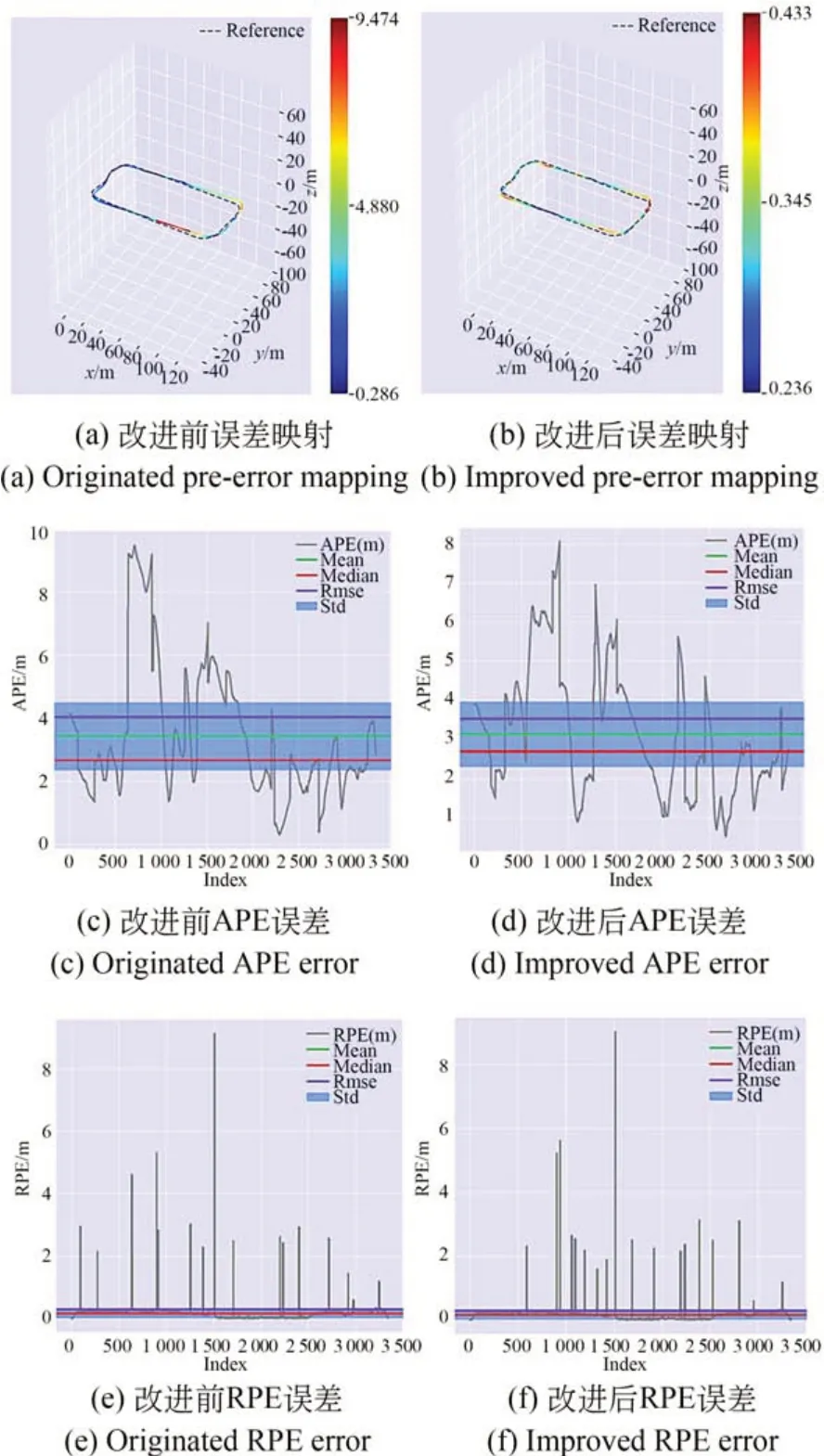
图6 SLAM 轨迹估计的误差分析Fig.6 Error analysis of SLAM trajectory estimation

对比图6（a）和图6（b），改进后算法的位姿估计误差变低。图6（c）和图6（d）表明，改进算法将绝对误差的Mean、RMSE、误差中位数（midian）以及标准差（std）限定在更小的范围内；而图6（e）和图6（f）表明，RPE 误差所代表的局部误差在算法改进前后没有明显区别。

为了更好地增强园区的三维建图效果，通过添加回环检测对点云地图进行回环修正消除累计误差，利用APE 与RPE 对添加回环检测的改进后融合算法进行分析，结果如图7 所示。

对比图6 和图7，在改进算法中添加回环检测后位姿估计误差变低，Mean，RMSE，midian 以及std 范围变小。根据APE 误差进行分布对比分析与误差箱型图，得到具体的误差分布规律，APE 误差分布如图8 所示。

由图8（a）可知，改进算法比原算法的APE误差分布更为平均，没有出现极其突出的误差。由图8（b）可知，改进算法没有存在异常值并将误差分布限制在更小的范围内。对录制的数据集进行bag 包的倍速播放再进行重复的误差分析，如图9 所示。

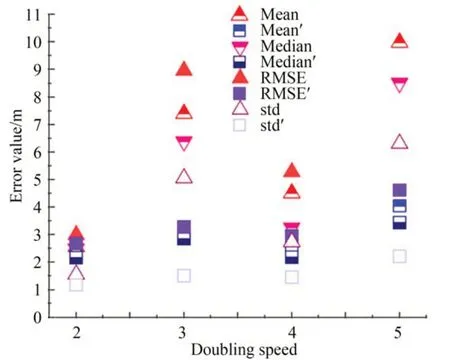
图9 倍速实验的APE 误差对比Fig.9 Comparison of APE error of double speed experiment

图9 分析得到，改进前算法的各项误差受倍速实验干扰时的影响较大，而改进后算法的误差都较为稳定。以z轴高度为颜色映射能直观地看出建图的高程效果，如图10 所示。以z轴为分割映射，调整点云颜色赋值为z轴并将蓝色设置为点云z轴坐标最低于1.5 m 处的点云，总体上随着高度变高颜色由蓝色变为红色，这样的操作可以确定蓝色部分为地面及其接近地面的点云，红色部分为其他高处环境点云，改进后算法点云在水平基准0 m 存在更多分布（SLAM 开始时，以起点处为高程为0）。

采用Cloudcompare 对改进前后算法生成的点云地图进行ICP 配准后，选取基准面并将截取的基准面点云分割切片，操作流程如图11 所示。将点云信息输出，去除反射强度时间戳等信息后只保留位置坐标信息进行分析，拟合线点云离散分布如图12 所示（彩图见期刊电子版）。

图11 拟合线信息提取过程Fig.11 Process of fitting line information extraction

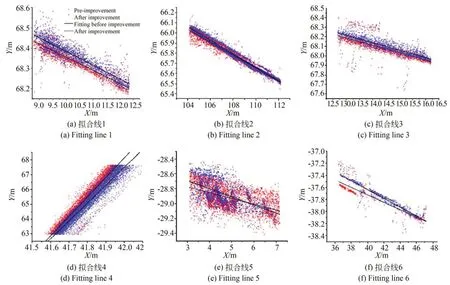
图12 点云的离散性分布分析Fig. 12 Discrete distribution analysis of point cloud

点云的拟合误差（位置坐标误差）是指拟合后的点云与实际点云之间的位置差异。位置坐标误差是一个相对值，它表示拟合后的点云与实际点云之间的差异。根据图12 的拟合线点云集合可以看出，大部分改进后的拟合线周围点云（蓝色）比改进前算法点云（红色）在它们各自拟合线附近有更多分布，同时分布区间更小更密集，集中在拟合线附近。通过分析误差也可以得出同样的结论，拟合线点云分布的各类误差与离散程度参数见表1。

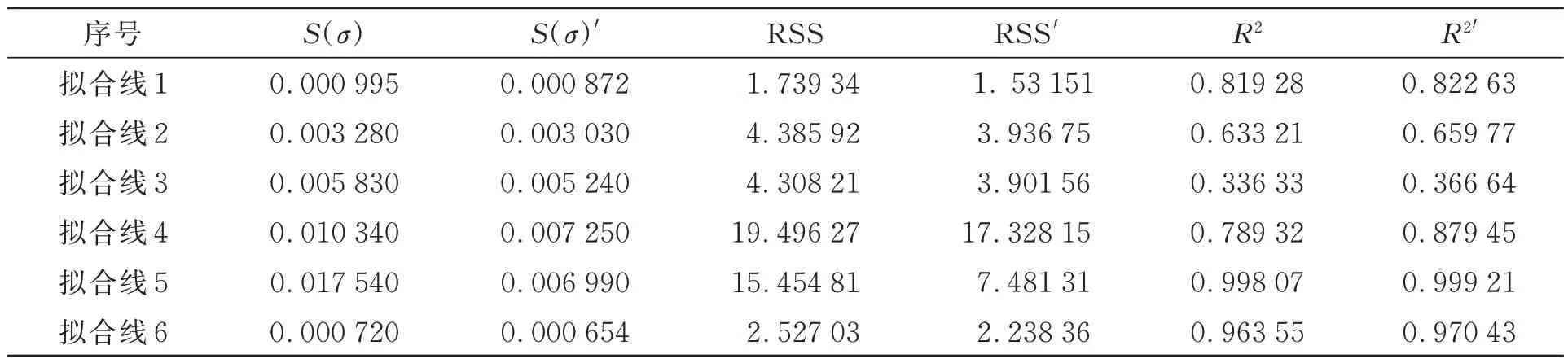
表1 拟合线误差的分析结果Tab.1 Analysis result of fitting line error

如表1 所示，改进后的算法在各个拟合线上的点云偏离拟合线的均方差（S（σ）′）和残差平方和（RSS′）相比于原算法的S（σ）和RSS 上都有改善，同时在评价偏离程度的参数上，改进算法的R²更接近1，表明在建图细节上改进算法比原算法的点云地图更加平整规律，一致性更好。

选取KITTI 数据集00，05，07，09 序号数据集进行仿真，所有场景对比APE 情况如表2 所示。在4 个KITTI 数据集上改进算法均优于其他算法，缩小了APE 的误差区间，改进算法的Mean 相较于原Fast-LIO2 算法，在KITTI 数据集00，05，07 和09 号场景下分别降低了12.09%，8.36%，7.50% 和 12.21%，平 均 下 降 了10.04%，改进算法的RMSE 相较于原算法在00，05，07 和09 号场景下分别降低了12.56%，14.56%，8.85% 和 12.19%，平均下降了12.04%。在选取的学校园区实地场景下，改进算法的Mean 较原算法降低了11.04%，改进算法的RMSE′较原算法降低了17.35%。

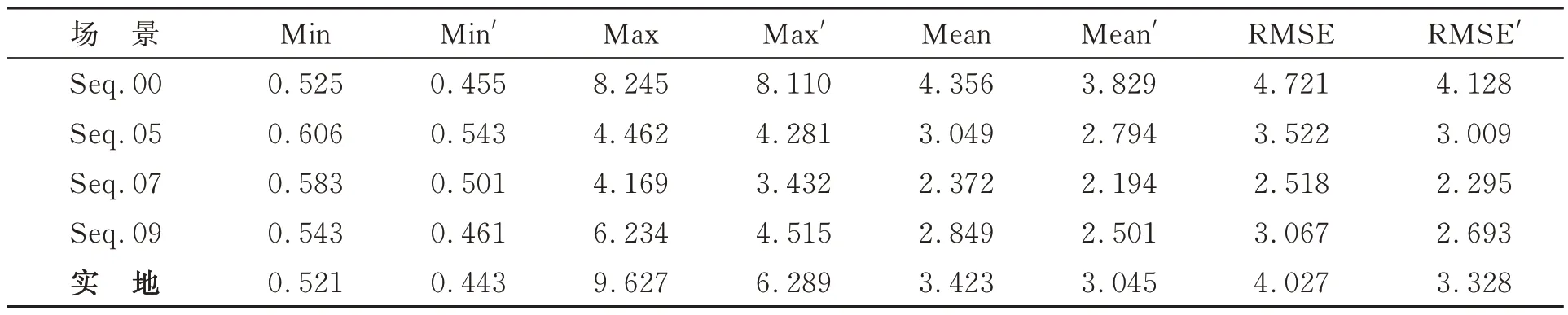
表2 算法APE 误差对比Tab.2 Comparison of APE error

5 结 论

本文将激光雷达与IMU 融合进行建图，通过添加IMU 因子和激光雷达里程计因子进行后端优化，引入ICP 回环检测对点云地图进行回环修正消除累计误差，利用iVox 结构改进Fast-LIO2 采用的iKD-tree 结构，通过APE 与RPE 进行评价分析。选取开源数据集与实地场景进行建图实验，改进算法在KITTI 数据集00，05，07 和09 号场景下的平均误差分别降低了12.09%，8.36%，7.50% 和12.21%，平均下降了10.04%，均方误差方面相较于原算法分别 降 低 了 12.56%，14.56%，8.85% 和12.19%，平均下降了12.04%。在选取的学校园区实地场景下，改进算法误差均值较原算法降低了11.04%，均方根误差较原算法降低了17.35%。