一维光学位置传感器融合的非接触多自由度位姿测量系统
莫嘉嗣, 陈健欢, 温远航, 梁杰俊, 陈秋烁, 闫国琦
(华南农业大学 工程学院,广东 广州 510642)
1 引 言
目前,机器人的运动控制方式一般可分为开环控制系统[1]、仅含关节反馈的半闭环控制系统[2]和包含关节反馈与末端反馈的全闭环系统[3]3 种。为了兼顾精度、成本和体积,大部分的机器人都是仅含驱动关节反馈的半闭环机构。半闭环机器人由于末端状态信息不能实时观测,需要进一步提高定位精度,这是一项很有挑战性的工作。
机器人末端执行器的位姿测量是机器人实现标定、实时反馈的关键技术,而缺乏合适的多自由度传感器实现末端位姿反馈则是机器人领域的共性问题。在缺乏末端测量反馈的前提下要提高机器人的末端定位精度一般采取两种途径,一是提高驱动关节定位精度,莫嘉嗣等采用自适应前馈补偿控制算法提高了平面3PRR 并联机器人驱动关节轨迹跟踪定位精度[4];二是使用标定算法对运动学参数进行标定,Mo 等采用误差模型结合辅助测量手段的改进标定算法提高了平面3PRR 并联机器人的末端定位精度[5]。尽管这两种手段能不同程度地改进机器人末端的定位精度,但是仍然存在不足。一方面,虽然驱动关节(一般是单自由度机器人)有能力实现高精度定位,但在驱动关节运动传递到末端的过程中,传动链会引入加工误差、装配误差、弹形变误差,以及齿轮传动误差等非线性因素[6]。这些非线性因素是不确定的,会导致末端定位误差的产生。这些非线性因素与误差来源在关节运动传递到末端运动的过程中是不可控的,同时误差在运动链中的传递又具有不确定性,因此单纯依靠提高驱动关节的定位精度对提高末端定位精度的作用是有限的。另一方面,采用标定方法虽然能提高末端定位精度,但并不是一种实时提高精度的方法,对于慢时变系统(例如刚性机器人),在标定后的短时间内是有效的,但不能保证长期有效;假如长时间工作后出现了磨损,或者由于生产需要而搬运机器人后重新安装,为了保证精度,必须再次重新标定参数,标定过程冗长复杂,影响工作效率。
为了进一步提高速度,降低由于惯性产生的动力学特性的影响,人们开始减轻机器人的质量,杆件越来越轻薄,柔性越来越大,并成为刚柔耦合机构。刚柔耦合机构是快时变系统,其运动过程复杂,充满不确定性,因此离线标定难以补偿其末端定位误差,机构的运动学参数在线实时辨识和末端实时反馈是提高刚柔耦合机构性能的有效手段。机构末端多自由度运动状态信息测量是实现机构运动学参数在线辨识、末端实时全反馈控制的关键环节,是制约机构性能的瓶颈之一,但就目前而言,尚缺乏集成的多自由度测量手段。
改进驱动关节控制算法或采用参数标定算法等手段都是间接提高末端精度的手段,但并不能从根本上解决问题。假如机器人驱动关节与机器人末端多自由度运动状态信息能够实时测量反馈,搭建机器人全闭环控制系统则可轻易实现奇异规避、振动抑制和轨迹跟踪等综合性控制,对提高机器人性能具有重要意义。
目前,比较先进的多自由度运动状态信息测量手段有拉线式位移传感器[7]、三坐标测量仪[8]和球杆仪[9]等接触式测量手段,以及激光跟踪仪[10]、光学运动跟踪系统[11]和机器视觉[12]等非接触测量手段。接触式测量由于妨碍了机器人的运动作业,一般只作为离线标定手段,并不用于机器人实时在线反馈。非接触式测量中的激光跟踪仪是目前精度和实时性最好的测量方式,具有测量精度高、测量速度快和测量范围广等优势[13],但需要在机器人末端装载对靶物,实际上也影响了机器人运动,而且测量的自由度有限。例如,激光跟踪仪搭载一个靶球,只能测量3 个平动自由度,若要测量姿态,需要两台激光跟踪仪同时工作或一台跟踪仪通过多个靶球分时解算[14]。天津大学在机器人末端固定4 个非共线的参考点,均能被激光跟踪仪测量,间接得出机器人末端的位姿[15]。此外,激光跟踪仪十分昂贵,并不适合长时间在生产现场对机器人进行实时反馈控制,一般只用于定期标定[16]。
机器视觉成本较低,使用灵活,常用于机器人末端测量。平面测量常用单目视觉,Li 等开发了一种单目视觉系统,用于在线测量3PRR 平面并联机器人的位姿[17]。但是单目视觉对焦距有一定的要求,难以集成到需要改变Z轴高度的运动机器人测量上[18];而且单目视觉在测量姿态上比较困难,往往需要辅以别的传感器,张天麟将姿态传感器和视觉传感器结合,以低成本的方式测量末端位姿,提高了测量精度[19]。机器视觉的测量速度与被测物体的复杂程度和相机的像素大小挂钩,测量复杂物体时,算法耗时较长,则响应速率不够;如果为了提高检测精度而提高像素,则数据传输量增大,响应速率降低;提高像素也会带来视场大小与检测高度的变化,使得机器视觉测量受限;在三维测量上,需要用多目视觉,多个相机安装在机器人上,其体积和质量势必会影响机器人的正常工作,而多目相机的标定也是目前的研究难点。尽管传统视觉位姿估计方法比较成熟,但是它特别依赖先验知识,自适应性和泛化性较差[20]。
综上所述,目前机器人末端测量反馈除了精度、实时性等基本测量要求外,还要求不增加太多的辅助结构,不影响机器人的正常工作。
多源传感测量通过搭建多传感器系统,对多传感器信息进行融合估计实现测量[21],可采用多种低成本传感器实现较高精度的测量,能较好地解决机器人末端多自由度测量反馈问题。Guo等使用3 个激光位移传感器融合,解算出柔顺并联平台的末端位姿后进行反馈[22]。本文提出一种采用多光学位置传感器(Position Sensitive Detector,PSD)融合的平面机器人3 自由度非接触测量装置与方法,在只需搭载十字线激光的前提下,可实现平面3 自由度机器人的高速、高精度测量和反馈,并且不受Z轴高度的限制,易于集成到更多自由度的测量系统中。
2 原 理
2.1 一维PSD 传感器测量原理
本文提出4-PSD 测量装置,采用4 个一维PSD 通过合理的位置摆放建立测量模型,实现平面3 自由度非接触测量的目的。该装置选用日本滨松公司的一维PSD 传感器,感光面积为2.5 mm×70 mm,光谱响应为400~1 100 nm,线性误差为0.3%,分辨率为10 μm。如图1 所示,一维PSD 传感器是P-I-N 结构,实际上是利用横向光电效应,采用连续的平面扩散型光电二极管,没有条带或盲区,能测量出一个光斑在它的感应面上的位置。
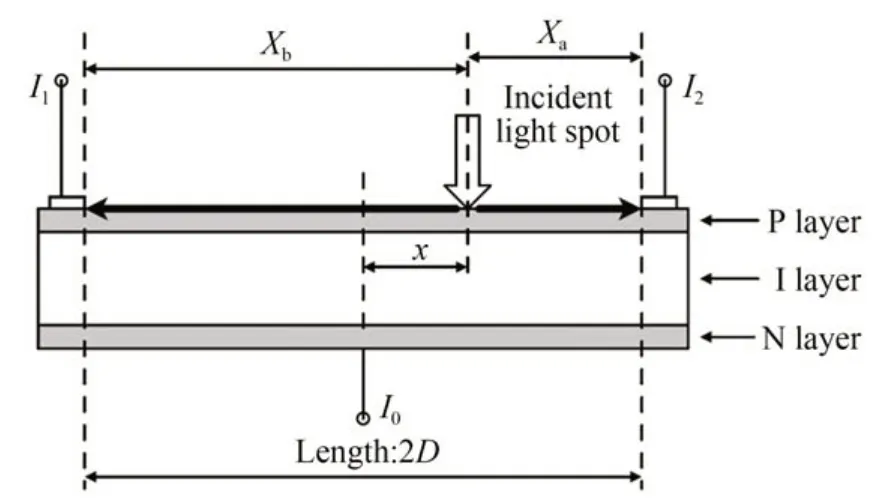
图1 一维PSD 传感器位置测量原理Fig.1 Measurement principle of one-dimensional PSD sensor
以感光面积的几何中心为原点,当有入射光照入到传感器的有效感光区域时,会产生二条通道的感应电流I1和I2,其测量动态范围宽,输出为模拟信号,因此,测量频率完全由处理电路的A/DC 采样频率决定,其值很高。2 条通道输出的感应电流与传感器的光斑位置关系为:
只要测得感应电流I1和I2就可以进一步计算得到光斑位置x。该传感器能测量到边缘的光斑位置,并且入射光斑形状、密度分布对测量位置读数基本没有影响,输入光斑可以是任意的尺寸和形状。这是因为输出信号由光斑中心的几何位置决定,即输出信号与光斑到PSD 感光区域中心的位移量成正比,为后续使用十字线激光(650 nm 红光)进行测量提供便利。
2.2 测量模型推导
通过一维PSD 传感器融合测量平面(x,y)自由度,首先采用正交(90°)十字线激光器对两个正交分布的PSD 传感器进行平移测量,但若十字线激光器光线与PSD 感光轴线不垂直(见图2),测量出的(x,y)会产生偏差,其原因是缺少绕Z轴旋转的α角度从而引入了误差。为了测量α角,可对称地放置4 个一维PSD 传感器,通过正交放置,配合十字线激光器,可以实现平面3 自由度(x,y,α)的非接触式测量,测量原理如图3所示。
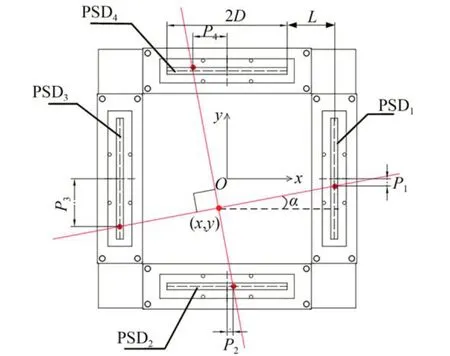
图2 光斑一维坐标与4-PSD 坐标系分布Fig.2 Distribution of one-dimensional coordinates of light spot and 4-PSD sensor coordinate system
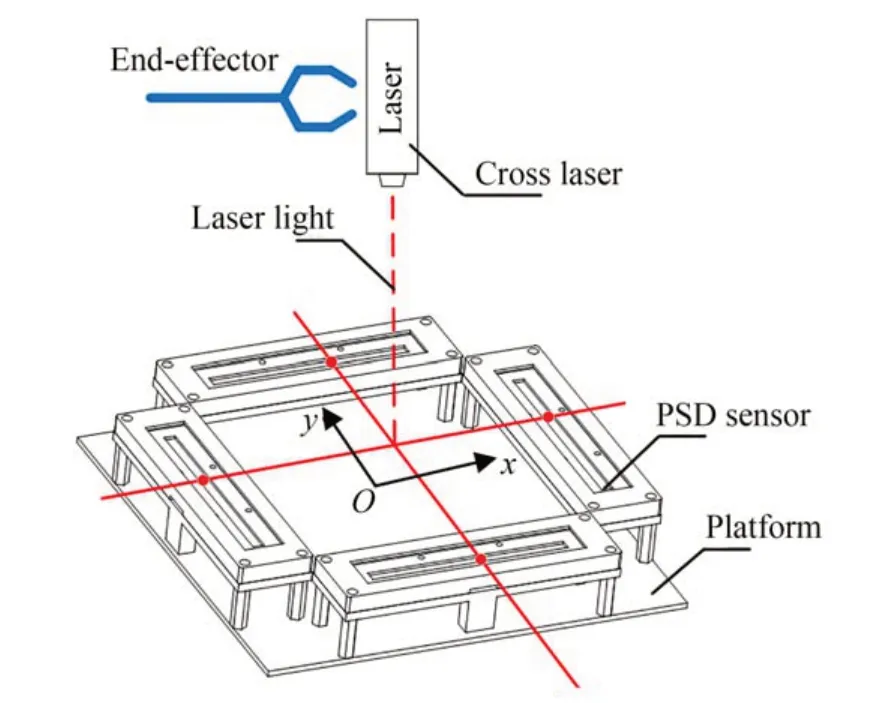
图3 4-PSD 融合测量原理示意图Fig.3 Principle diagram for 4-PSD fusion measurement
4-PSD 装置定平台固定部分由4 个一维PSD传感器首尾相接,正交(90°放置)分布在传感器安装底板四周。机器人末端搭载十字线激光器,当机器人运动时,末端激光线将会与定平台上各PSD 传感器有相对位置变化。以定平台安装底板的几何中心为坐标原点O建立坐标系,如图3所示。
如图2 所示,X轴与PSD2,PSD4平行,Y轴与PSD1,PSD3平行。激光器发出正交(90°)十字线激光,投影在4-PSD 装置上。十字线激光的4 段光线分别照射在4 个PSD 上,其照射光斑产生的感应电流代入式(1),计算得到局部一维坐标P1,P2,P3,P4。PSD1上光斑的二维坐标为(D+L,-P1),PSD2上为(-P2,-(D+L)),PSD3上为(-(D+L),P3),PSD4上为(P4,D+L)。通过PSD1 和PSD3 感光点的直线为L1,通过PSD2和PSD4 直线为L2。L1的斜率k1=-(P1+P3)/2D′,截距b1=P3-(P1+P3)/2;L2的斜率k2=2D′/(P2+P4),截距b2=D′-2D′P4/(P2+P4)。安装偏移量为L,L1的方程为y=k1x+b1,L2的方程为y=k2x+b2,联立后求解可得交点坐标,即激光线中点的(x,y),再通过斜率k1和k2可得α角,即推导出4-PSD 测量模型如下:
式中:D为PSD 传感器感光部分长度的一半,k1和k2为激光线斜率,b1和b2为激光线截距,α为末端绕Z轴逆时针旋转的夹角。
机器人末端与激光器是固定连接的,激光器体积小,质量轻,对机器人末端工作几乎没有影响。故通过本装置可以非接触式地测量机器人末端的平移和旋转,共3个自由度的位姿(x,y,α)。
2.3 一维PSD 信号处理与采集电路设计
式(2)中关键变量为4 个PSD 传感器的测量结果P1~P4。为得到每个PSD 的测量结果,根据式(1)设计信号处理电路,如图4 所示。PSD 传感器产生的信号I1和I2是电流信号,不能直接通过A/DC 进行采样,需要经过前置信号调理电路,转换成U1和U2后进行运算和采集。这里U1(U2)和I1(I2)是线性比例关系,若放大电路倍数为1,已知2D=70 mm,由式(1)转变为式(3),电压信号U1和U2经过运算得到:
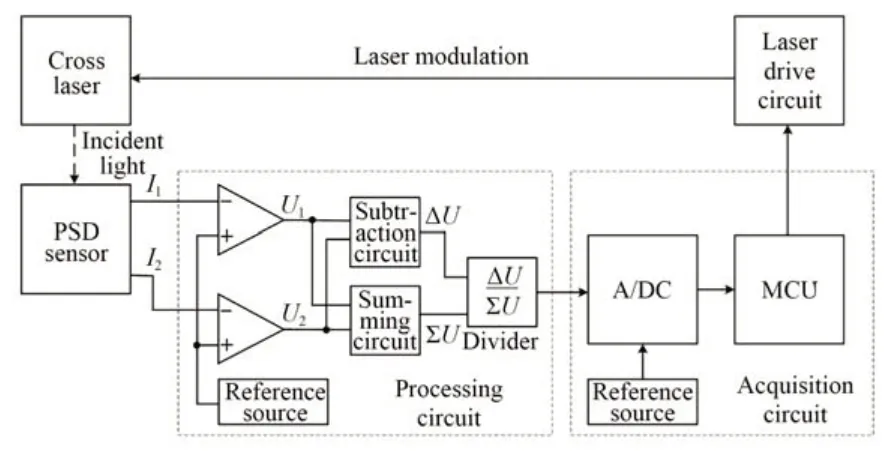
图4 PSD 信号处理与采集电路设计方案Fig.4 PSD signal processing and acquisition circuit design scheme
其中x为一维光斑位置。
图4 的前置调理电路使用积分电路(见图5),可完成两个任务:一是通过R1和C1将PSD 感应电流进行I/V转换和信号放大,以满足A/DC的信号接收(±10 V)要求;二是作为硬件滤波方式使用C和Rf进行低通滤波,去除绝大部分的高频电信号干扰,提高测量信号的稳定性。

图5 信号调理电路Fig.5 Signal conditioning circuit
2.4 测量系统软硬件组成
如图6 所示,4-PSD 系统由上下位机组成,下位机主控为STM32F103C8T6 单片机,负责单个PSD 传感器信号的采集和传输。单个PSD 传感器的两路电流信号通过前置调理后变成U1和U2电压信号,经过加法电路、减法电路和模拟除法器AD633 计算后得到实际光斑距离信号,再通过由AD7606 和STM32F103C8T6 单片机组成的A/DC 采集电路后,与上位机软件通过USB-HID协议传送数据,最高频率为1 000 Hz。这里采样频率为50 Hz,能满足一般需求。

图6 4-PSD 测量系统原理与标定装置Fig.6 Schematic diagram and calibration devices of 4-PSD measuring system
上位机为PC 上编写的C#程序界面,主要负责USB-HID 通讯、数据采集记录、测量模型(公式(2))计算、数据可视化和标定等功能,如图7所示。

图7 4-PSD 测量系统上位机程序Fig.7 Man-machine interface of 4-PSD measuring system
3 实验与结果分析
3.1 实验装置
4-PSD 测量实验装置如图8 所示,十字激光器通过固定板固定在4-PSD 装置上空某平面,通过步进电机调整转角。使用步进电机控制器分别控制精密XY位移平台、激光角度调整机构运动,以2 个激光位移传感器输出的位置信息作为标准参考值,可对4-PSD 测量装置测得的3 自由度位置信息进行标定。

图8 4-PSD 实验装置Fig.8 Photo of 4-PSD experimental setup
3.2 环境光干扰降低
对PSD 信号进行预测试,结果如图9 所示。黑色曲线是对单个PSD 其中任意一点只有硬件滤波的信号调理电路进行实验观察的结果,虽然滤除了高频干扰,但是仍然存在数据波动。对数据进行快速傅里叶变换分析离散数据频谱,发现干扰信号的频率主要分布在0~5 Hz,属于低频干扰,主要为环境光影响。干扰信号在一定程度上会增加系统测量误差,因此需要采取降低环境光干扰的相应措施。

图9 激光调制去环境光干扰效果Fig.9 Laser modulation to remove ambient light interference effect
PSD 传感器在有光的地方会感应出光电流,用单片机I/O 口输出脉宽调制(Pulse Width Modulation, PWM)脉冲驱动十字线激光器,可减弱环境光干扰的影响。当驱动波形为低电平时,激光器关,输出信号Uoff(仅包含环境光信号);当波形为高电平时,激光器开,输出信号Uon(包含环境光信号+激光器信号),一个周期内采样两次,经单片机内的数值相减便可得到去环境光后的采集电压,如图9 所示。此信号为减弱了环境光干扰幅值后的信号,但由于激光器开、关的两次采样不是同时进行的,导致信号采集至少有半个周期的滞后,所以环境光产生的低频干扰只能减弱,不能完全消除,信号仍有环境光残留影响,因此需要通过后续的软件滤波和标定手段来提高测量系统的精度。
3.3 实验误差分析
标定平台如图8 所示,固定十字激光器垂直于4-PSD 装置的中心原点后,通过步进电机控制的精密XY位移平台带动4-PSD 装置。2 个激光位移传感器垂直置于平台两侧,用于记录4-PSD装置的平面位移,X轴运动记为激光位移传感器X,Y轴为激光位移传感器Y,同步采集两者输出的电压值与4 个PSD 传感器对应输出的电压值(6 个通道)并传输至上位机,图10 为控制步进电机滑台运动一个直径为35 mm 的圆。

图10 4-PSD 测量误差分析Fig.10 Error analysis of 4-PSD measurement
预实验发现,4-PSD 测量装置存在激光光源、温度、环境光和装配误差等影响;另外,PSD信号在经过硬件滤波和激光调制后,每个环节都引入了信号失真,虽然信号质量更高,但是却导致一维PSD 出现线性失真,4-PSD 测量装置出现非线性失真。测量得到的位置信息包含综合性偏差,最大误差达到4.98 mm,如图10 所示。此外角度旋转变化虽然准确,但却会引起位移的耦合偏差。
3.3.1 数字滤波算法实验结果与分析
父母离婚的那天,父亲狠狠地打他,骂他“败家星”。母亲大病了一场,精神恍惚。父亲给了微薄的赡养费,母亲说,如果你要了,就不是我儿子。于是,他只有去打工。父亲渐渐成了这个城市的有钱人,开着名车一次次从他身边经过要把钱给他,他拒绝,他恨这个男人。母亲去世后,4年大学,他靠助学贷款,又打了好多工,熬了过来。他不会原谅父亲。父亲越来越有钱,还放出话来,穷死他,我一分钱都不会留给他!他冷笑,我一分钱也不会要!24岁那年,他得了一场病,医生问他家属是谁,他吓了一跳,他知道自己病得很重,便打电话给父亲。
为了得到最适用于PSD 调理电路的数字滤波算法,本文分别进行了算术平均值滤波法、中位值滤波法、中位值平均滤波法、一阶滞后滤波法和加权递推平均滤波法的实验,并对比它们的滤波效果。使光斑照射在PSD 同一位置点,在软件中分别加入5 种数字滤波算法,效果如图11 所示,加入数字滤波后的数据稳定性均有不同程度的改善。
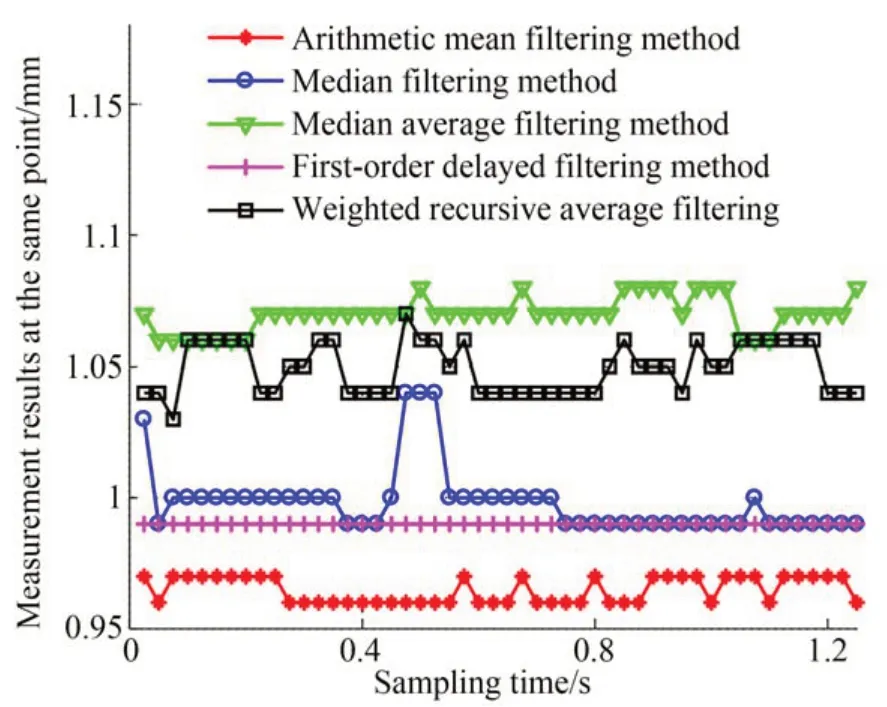
图11 加入多种滤波算法后的信号Fig.11 Signals after adding variety of filtering algorithms
由图11 可知,未加入任何滤波算法时测试得到的数据波动较大,经过滤波算法后,测量数据的波动情况变得平缓。数据对比如表1 所示,虽然略有波动,但能满足系统测量数据的稳定性要求。

表1 滤波前后不同滤波算法的数据对比Tab.1 Comparison of various filtering algorithms before and after filtering
在测试稳定性的同时,不能忽略系统的实时性。对于算术平均滤波法、中位值滤波法、中位值平均滤波法和加权递推平均滤波法,在程序启动后就可以测出即时位置数据,实时性较好;但是一阶滞后滤波算法的实时性较差,等待较长时间才能得到测量值。
如图11 所示,滤波算法存在失真,所以不同滤波算法得到的测量数据存在波动,导致图上纵坐标的绝对位置不一样,因此在滤波之后要进行位置修正。位置修正后便于观察误差,误差分析如表2 所示。
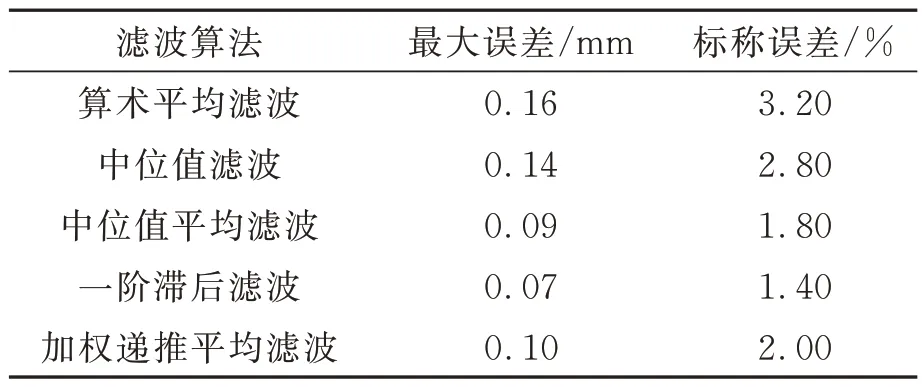
表2 线性修正后各种滤波算法的数据对比Tab.2 Data comparison of various filtering algorithms after linear correction
综合分析可知,一阶滞后滤波法的实时性较差,中位值滤波法和算术平均滤波法的误差精度较低。相比之下,中位值平均滤波法的误差较低,既能过滤随机干扰信号,又能过滤脉冲干扰,有较好的实时性、稳定性和准确性。
3.3.2 标定方案设计
滤波后的4-PSD 测量系统减弱了随机误差的影响,但误差的影响因素会随使用环境而变化。实验发现,仅滤波处理并不能使测量装置适用于各种环境,由于激光器、调理电路、采集电路等的综合影响,其输出信号与光斑运动之间存在一定程度的非线性,需要通过标定来补偿。
为了进一步降低误差,需要对装置进行末端的实测标定。标定的参考基准为激光位移传感器的测量结果,激光位移传感器的安装如图8 所示。采用抗干扰能力较强的Panasonic HGC1100 激光位移传感器(测量范围为±35 mm,分辨率为0.01 mm,精度为0.07 mm),分别进行单个PSD 的线性校正和4-PSD 装置的二阶非线性拟合,进一步提高系统稳定性和准确性。
标定处理分为逐个PSD 传感器的线性校正和4-PSD 合成轨迹的多项式拟合(二阶非线性校正)。标定的参考为激光位移传感器输出,将4-PSD 的输出结果向激光位移传感器的测量结果上进行逼近。由先前的误差分析可知,4-PSD 测量装置存在线性、非线性误差。其中线性误差如图12 所示,即理论上一维PSD 传感器的光斑移动距离与输出电压的关系是成正比的,因误差使得测量数据存在线性漂移。

图12 一维PSD 线性失真Fig.12 One-dimensional PSD linear distortion
控制4-PSD 装置沿X轴做匀速直线运动,轨迹数据如图13(a)所示;控制激光器旋转近30°,其位移偏差如图13(b)所示。可以看出,标定前4-PSD 测量装置测得的数据存在明显的误差。
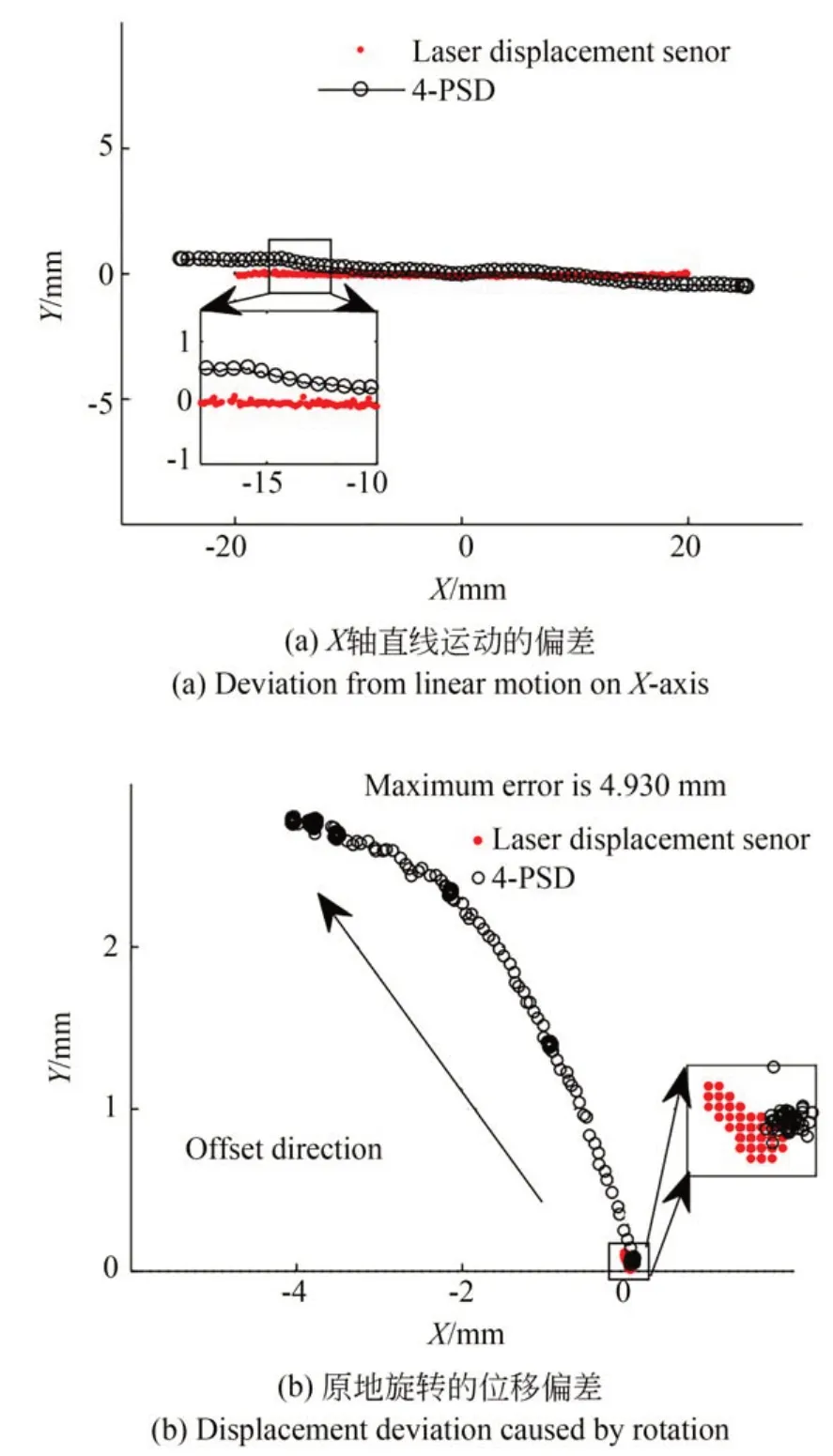
图13 未标定前的平面位移和角度旋转变化Fig.13 Changes in plane displacement and angle rotation before calibration
由于4-PSD 测量装置是基于各个PSD 传感器的信号输出,所以首先需要将平台上的PSD 传感器逐个校正。如图14 所示,分别移动X轴、Y轴,记录PSD1 的输出信号变化。结合图13 和图14 的实际测量数据可知,4-PSD 测量装置存在误差倾斜角为0.537°,同时测量轨迹与实际轨迹的两点误差最大为5.11 mm。因此,实验中将数据一次项拟合,开展补偿校正、倍数校正、原点校正等措施。
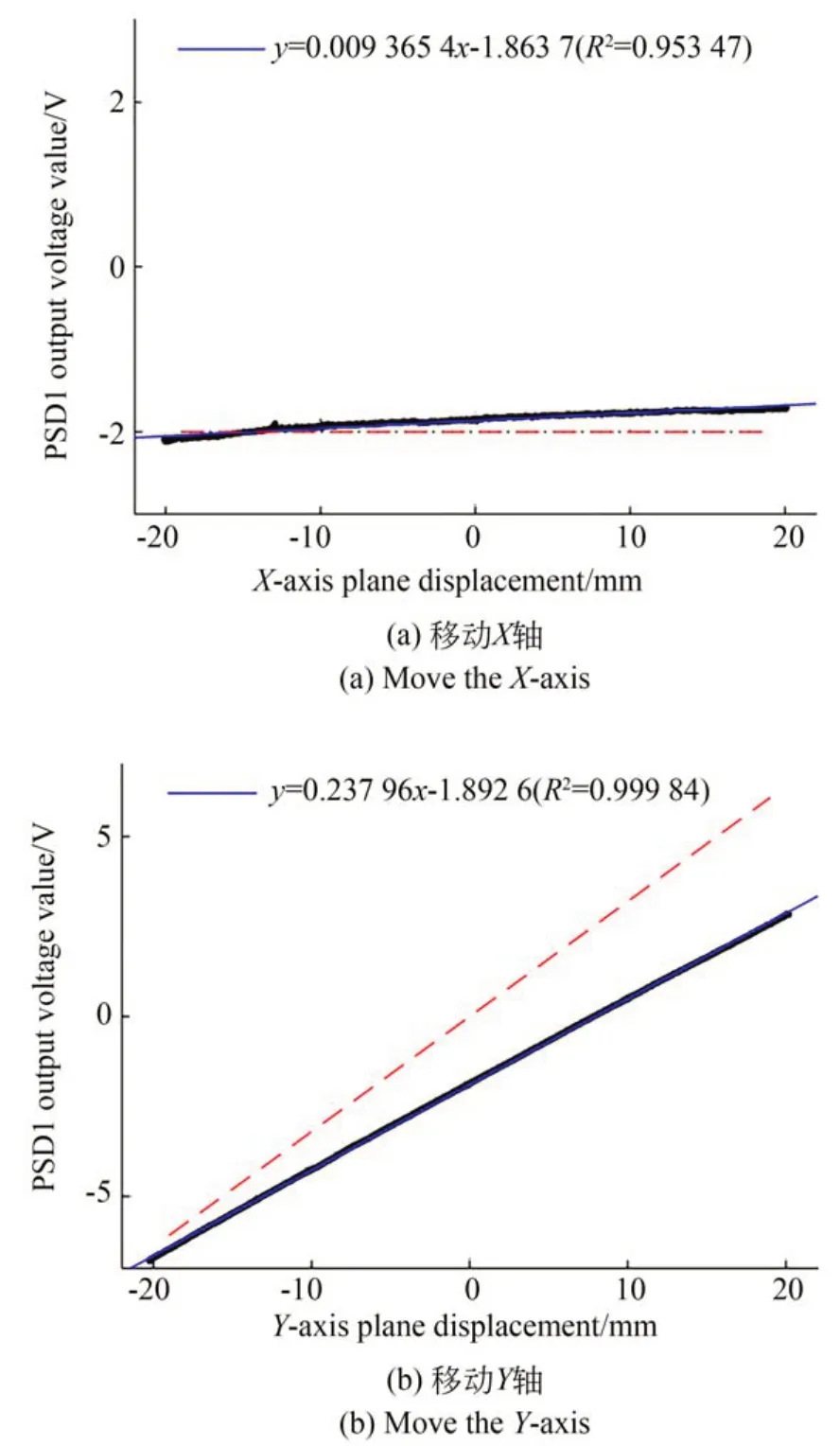
图14 PSD1 输出与XY 轴直线运动关系Fig.14 Relationship of PSD1 output and horizontal XY axis linear motion
移动X轴,记录PSD1对应的位移变化Δx和激光位移传感器X的输出xref,代入式(5)进行补偿校正;移动Y轴,记录PSD1对应的位移变化Δx和激光位移传感器Y的输出yref,代入式(6)进行倍数校正。再保持4-PSD 装置不动,根据式(7)进行原点校正,最后代入式(8)即得到PSD1传感器的线性校正公式。
其中:P1为PSD1传感器的初始激光感应距离,Pmm1为PSD1传感器经过校正后的激光感应距离(PSD2,PSD3,PSD4同理)。将4 个Pmmi代入计算式(2)和式(3)即可得到坐标(x,y,α)。
如图14 虚线所示,校正后,当平台沿X轴走直线时PSD1输出电压近似不变,而沿Y轴走直线时其输出电压与相对位移有线性正比关系。
控制4-PSD 装置走圆形轨迹,对所得到圆形轨迹坐标组(x,y)和(xref,yref)进行回归分析(多项式拟合)从而减弱线性、非线性误差。分别对上述两组坐标组进行一阶拟合和二阶拟合。最后将得到的单个PSD 线性校正转换关系式和4-PSD 坐标拟合关系式结合,共同作为4-PSD 测量装置的标定公式。
3.4 标定实验结果与分析
根据上述标定方案设计,标定处理分为线性校正和多项式拟合。线性校正主要是去除测量装置的线性误差。多项式拟合中包含了一阶拟合与二阶拟合,一阶拟合是对线性校正做进一步的线性迭代收敛,弥补线性校正过程中的数据偏差;二阶拟合则是以抛物线方式缩小测量过程的非线性误差。
如图15(a)所示,经过线性校正后位移轨迹较为接近真实值,误差倾斜角为0.019°,测量轨迹与实际轨迹的两点误差最大为0.52 mm,有较好的校正效果。而当激光器旋转角度近30°时,4-PSD 测量装置测得的位移误差如图15(b)所示,位移误差会随角度的变化而变化,最大误差为1.38 mm,分析得知该误差是由于激光器的4 条光线不均匀导致,为减弱该非线性误差需要进行多项式拟合处理。

图15 线性校正后的平面位移和角度旋转变化图Fig.15 Changes in plane displacement and angle rotation after linear correction
在进行多项式拟合时,第一步是控制4-PSD装置走圆形轨迹,通过记录到的两组激光位移传感器坐标数据进行一阶拟合;第二步是4-PSD 装置再走一次圆形轨迹,进行二阶拟合。一阶拟合后的运行轨迹如图16 所示,最大误差为0.35 mm。整体上,轨迹接近于真实位置信息,但在坐标(17.5,0)附近的测量轨迹弧度存在较小的非线性干扰,该区域的曲线较其他区域的曲线不够平滑,且整体误差较大的部分就在该区域。
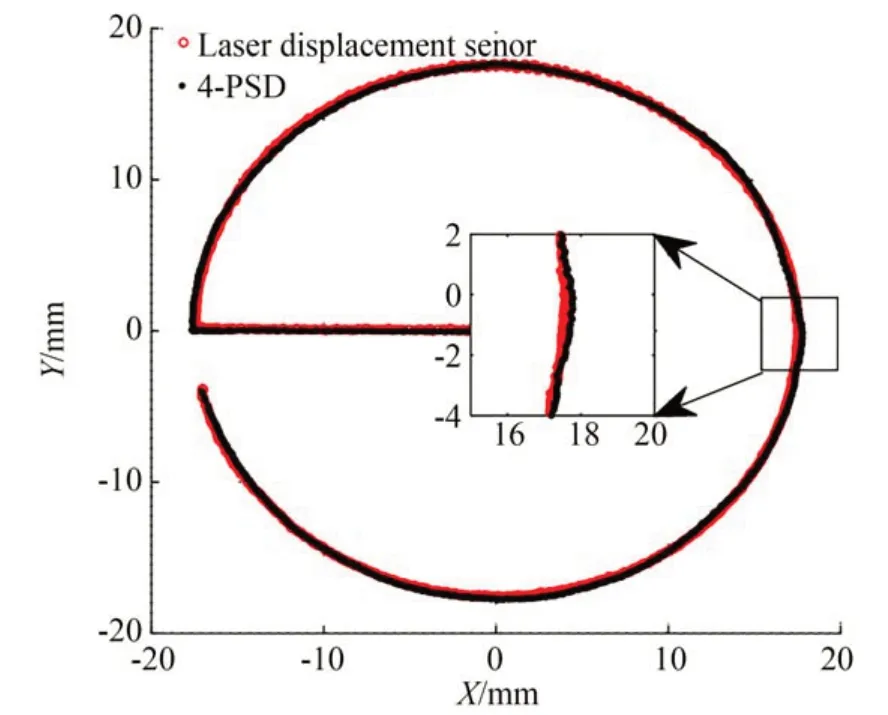
图16 一阶拟合后的圆形轨迹图Fig.16 Circular trajectory map after first-order fitting
二阶拟合完成后,运行圆形轨迹如图17 所示,抛物线的拟合对非线性误差有一定的削弱效果,在(17.5,0)附近区域的轨迹圆滑性得到了较好的改善。此外,二阶拟合后圆轨迹的最大误差为0.26 mm。

图17 二阶拟合后的圆形轨迹Fig.17 Circular trajectory map after second-order fitting
多项式拟合后进行角度耦合误差的测试,令XY滑台不动,只控制激光器旋转角度变化,从16.61°旋转至-16.34°。如图18(a)所示,角度计算结果变化平滑且准确度高,相对误差为0.24%。位移耦合偏差如图18(b)所示,在旋转过程中最大误差为0.34 mm,因为在17.5 mm 半径圆形轨迹的误差为0.26 mm,两处误差相差不大,可认为属于同一精度级别。因此,多项式拟合后角度旋转引起的位移误差在允许的精度范围内。
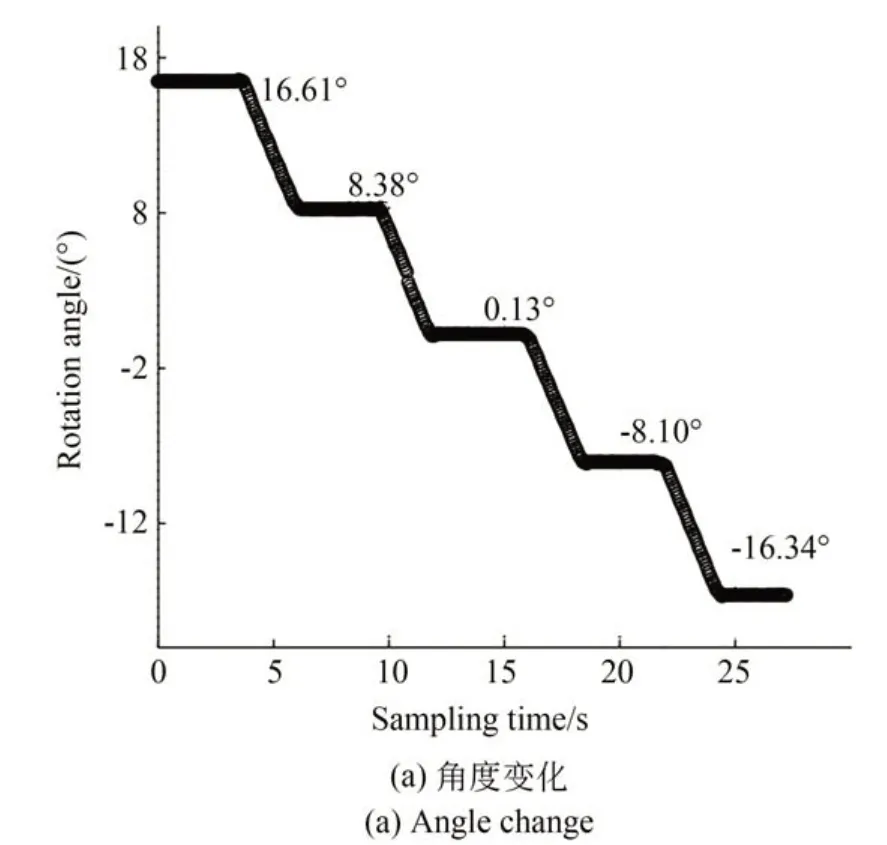
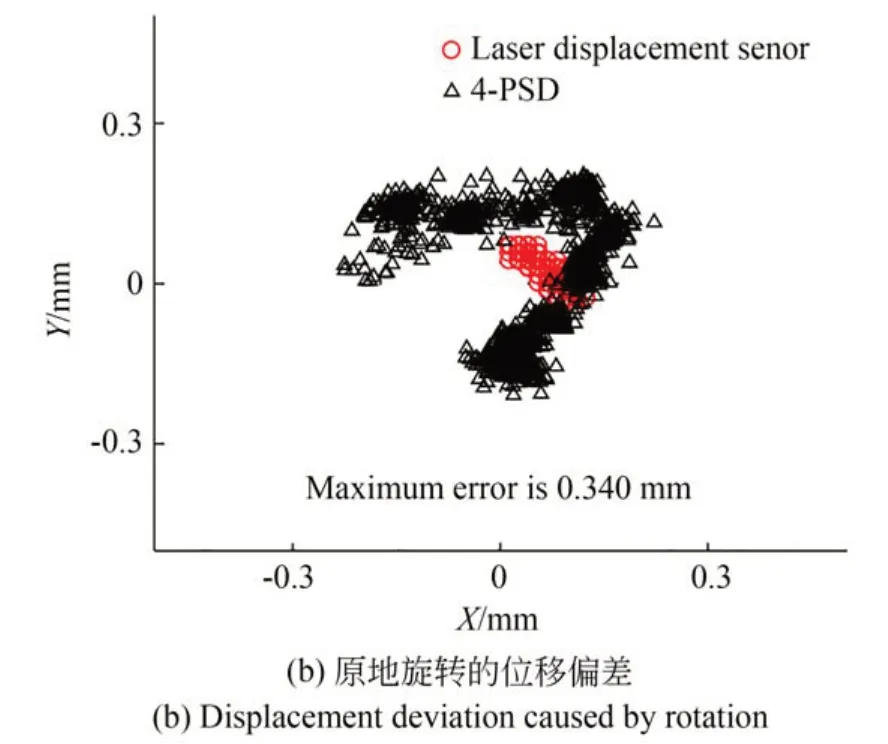
图18 多项式拟合后的角度旋转变化Fig.18 Angle rotation change after polynomial fitting
3.5 标定结果验证
分析实验结果曲线可知,测量系统的工作范围越大,其误差影响就越大。为了便于直观了解测量系统的实际误差分布,如图19 所示,采用棋盘格均匀布点方式呈现测量系统经标定后的测量精度分布。

图19 4-PSD 装置测量精度分布Fig.19 Accuracy distribution in 4-PSD device measurement
4-PSD 测量装置经过标定后,根据图19 采样点分布,移动激光器至布点图的采样点上并记录该点误差,绘制误差分布曲面如图20 所示,绘制误差分布等值线如图21 所示。由图可知,整个测量区域内,越接近坐标原点,其测量误差越小,在位于原点对称的20 mm×20 mm 的区域内最大误差为0.31 mm,边缘部分由于存在激光器光源质量、以及PSD 传感器感光材料性能等因素,误差较大,最大时达到0.68 mm。整体上,4-PSD测量装置标定后的精度有明显改善,全范围的平均误差为0.49 mm,比图10 的误差降低了90%,可满足大部分平面3 自由度测量的应用场合要求。
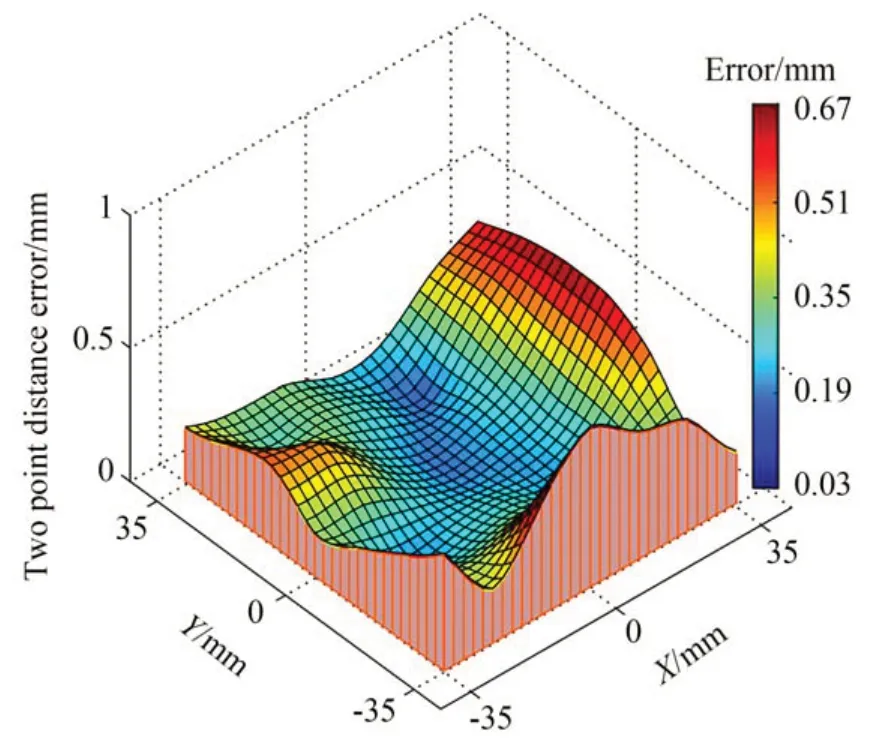
图20 4-PSD 测量系统误差分布曲面Fig.20 Distribution surface of 4-PSD measurement system error
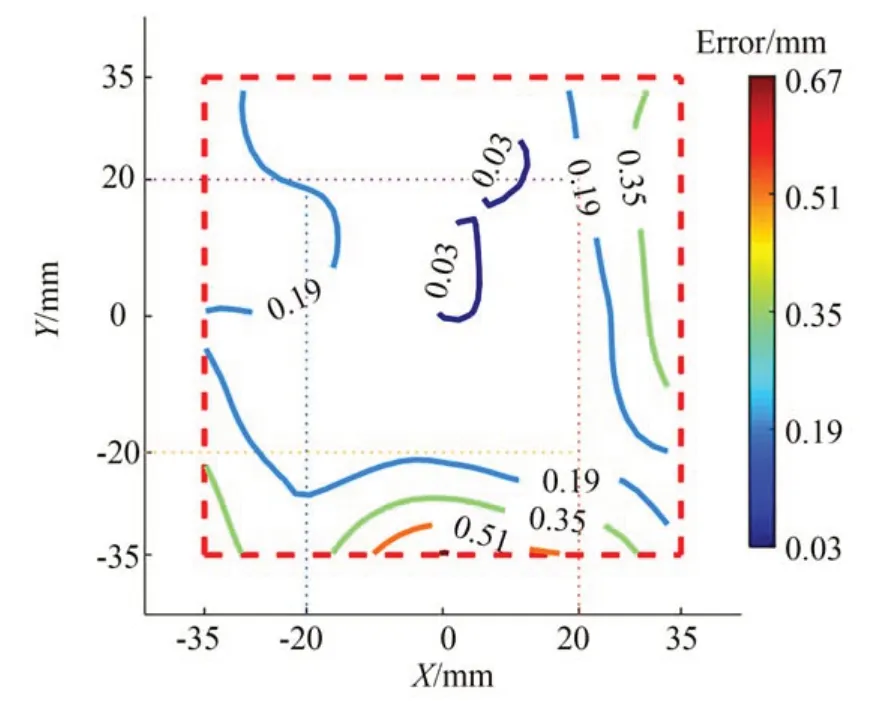
图21 4-PSD 测量系统误差分布等值线Fig.21 Distribution contour of 4-PSD measurement system error
4 结 论
本文针对现有机器人多自由度位姿检测方法的不足,提出了一种利用多PSD 传感器优化配置,对运动机构平面三自由度进行非接触式检测的方法,并搭建了4-PSD 测量系统,解决了常规传感器难以一次性测量平面3 自由度的问题;得益于PSD 传感器的高精度和高响应频率,该测量系统可满足大部分机器人末端位姿实时测量反馈的要求。基于PSD 的工作原理设计了基于单片机的一维PSD 传感器信号处理电路,得到了电压信号与光斑位置的映射关系;其次,为了使4-PSD 能在具有环境光干扰的场景下使用,对数据采集时的信号干扰问题开展硬件滤波、激光调制和数字滤波等实验,对PSD 从信号端到输出端进行处理,处理后的信号干扰变少,消除了环境光影响;但信号处理同时引入信号的线性和非线性失真,最后,通过分析4-PSD 测量装置的线性、非线性误差,设计了包括线性校正、多项式拟合的标定方法,弥补了环境光信号处理引入的失真,标定后系统在20 mm×20 mm 区域内的最大误差仅为0.31 mm。实验结果表明,在70 mm×70 mm 内测量系统的平均误差为0.49 mm,比标定前降低了90%。本文的测量装置和方法为机器人末端高精度、高速率的实时测量反馈提供了技术手段和理论支撑。

