基于卡尔曼滤波的激光外差干涉位移测量误差补偿

周志鹏， 楼盈天， 王升帆， 陈 宇， 陈本永

（浙江理工大学 信息科学与工程学院，浙江 杭州 310018）

1 引 言

激光外差干涉测量具有分辨率高、抗干扰能力强等优点，被广泛应用于超精密测量、工业制造等领域，是生产精密零部件和检测的关键技术［1-3］。在激光干涉位移测量中，可采用角锥棱镜或者平面镜作为测量镜。由于测量镜与被测对象刚性连接，位移测量结果存在多自由度运动误差。以角锥棱镜为测量镜，位移测量结果与偏摆、俯仰和滚转三个转角误差以及垂直、水平直线度误差两个平移误差耦合。角锥棱镜随被测对象旋转时，转角虽然不改变反射光束方向，但会带来测量光轴上的线位移测量误差，且转角和直线度误差耦合而产生光束平移，导致波前相位移动而产生额外的位移测量误差。相较于角锥棱镜，平面镜因其特性，其位移测量结果不受滚转误差、垂直与水平直线度误差的影响，只与偏摆、俯仰两个转角误差耦合。平面镜随被测对象旋转时，转角会引入测量光轴上的位移测量误差与反射光束方向变化而产生的位移测量误差。平面镜位移测量相对容易实现转角误差解耦［4-5］。

为消除上述平面镜旋转带来的位移测量影响，需先测出测量镜转角［6］，再根据转角与位移的解耦数学模型对位移进行补偿。相比于偏振泄露等因素造成的非线性误差，测量镜转角误差会给位移测量结果带来更大的影响［7-8］。目前，激光外差干涉仪转角测量有激光准直方法［9-11］，该方法在测量位移的同时，用位置敏感探测器（Position Sensitive Detector， PSD）等辅助工具探测光斑位置的变化来测量转角。Feng 等［12］提出了一种可进行六自由度同时测量的激光外差干涉装置，采用外差干涉原理测量位移，转角通过位置光电探测器和凸透镜测得的光斑位置偏移量算得。Zhang 等［13］提出了一种带有转角补偿的激光外差干涉仪，改进光路设计用偏振分光镜PBS 把测量光另分开一束结合凸透镜和位置敏感探测器进行测量镜的转角测量。Ren 等［14］也是采用位置敏感探测器和凸透镜对二维转角进行测量，建立姿态角测量模型和分析光斑畸变，并且采用样条插值法减小了PSD 非线性的影响。Wang 等［15］提出转角测量系统，还分析了透镜和PSD 轴向、径向等安装偏离误差并且进行校正，提高了转角测量精度。

这类激光准直方法大多利用凸透镜和位置敏感探测器探测光斑位置变化来进行转角测量，然后根据测得转角对位移进行补偿。因此，位移测量精度取决于转角的测量精度，而转角的测量精度取决于光斑位置变化量的探测精度。但是在实际应用中，探测器噪声等因素限制了光斑位置测量的稳定性和准确性，导致后续转角测量误差，为此需要对光斑位置信号进行降噪处理。

本文利用PSD 检测激光外差干涉仪测量镜转角导致的光斑位置变化，通过输入光斑位置信号观测数据，采用卡尔曼滤波对光斑位置状态进行预测，对含噪声的光斑位置信号进行处理，求得误差为最小的真实信号估计值［16-19］，从而对光斑位置信号进行降噪，获得更为准确的转角测量结果，再根据补偿模型对位移测量结果进行补偿，最终实现高精度的激光外差干涉位移测量。

2 基于卡尔曼滤波算法的光斑位置测量

2.1 测量原理

PSD 能够根据探测光斑位置输出4 路光电流［20-21］。将PSD 的4 个光电流进行运放后，可以得到包括光斑位置水平方向电压信号Vx、垂直方向电压信号Vy和总电压信号Vsum，分别表示为：

式中：IA，IB，IC和ID是二维PSD 表面电极产生与光斑位置相关联的4 个光电流，R是运放电路的等效电阻。

通过模数转换器ADC 对PSD 三路代表光斑位置的直流电压进行采集，FPGA 采用卡尔曼滤波算法对ADC 采集的直流电压信号进行滤波去噪。以电压信号Vx为例，建立卡尔曼预测信号电压模型为：

对信号电压Vx进行最优状态估计，即此刻滤波后的电压为：

式中：Vxk为此时ADC 采集到的信号电压Vx，Gk为卡尔曼滤波增益。Gk可表示为：

式中：Pk-1为上一刻的电压估计误差协方差，q为过程噪声协方差，该值反映相信电压信号预测值的程度。最后更新电压估计误差协方差为：

1.3 口腔黏膜炎分级标准［12］ 参照WHO抗癌药急性及亚急性毒性反应分级标准，将口腔溃疡分为0～3度，0度:无任何口腔不适;I度:口腔黏膜干燥、潮红、变薄，未有破损，进食时可有轻触痛;Ⅱ度:局部口腔黏膜有轻微破损、脱皮，破损灶不超过3个，范围不超过3 mm ×3 mm，进食时伴有明显疼痛;Ⅲ度:口腔黏膜多处溃烂、出血，伴有剧烈疼痛，且范围超过3 mm×3 mm，不能进食。

根据式（6），可得到卡尔曼滤波降噪后的电压信号V′x，同理可以得到降噪后的电压信号V′y和V′sum。最后对滤波后的三路电压信号进行运算，可得到光斑的二维位置信息为：

式中：w为位置敏感探测器探测面的横向边长，h为位置敏感探测器探测面的纵向边长。

综上，基于卡尔曼滤波降噪的光斑位置测量的具体流程如图1 所示。首先对PSD 三个端口电压信号进行同时采集，然后对这三个电压信号进行卡尔曼滤波；在滤波算法中，先给滤波电压值Vk-1和电压估计误差协方差Pk-1赋初值，再修正先验电压值和先验电压估计误差协方差，算出实时采集的电压与先验电压估计值的差，对滤波输出电压Vk、卡尔曼增益Gk和电压估计误差协方差Pk进行预测；预测完再次循环进行修正，不断迭代，最终输出稳定的位置电压信号。对PSD 三个端口的位置电压同时进行卡尔曼滤波降噪后，再根据位置电压信号和光斑位置的关系式即可得到去噪后的光斑二维位置。

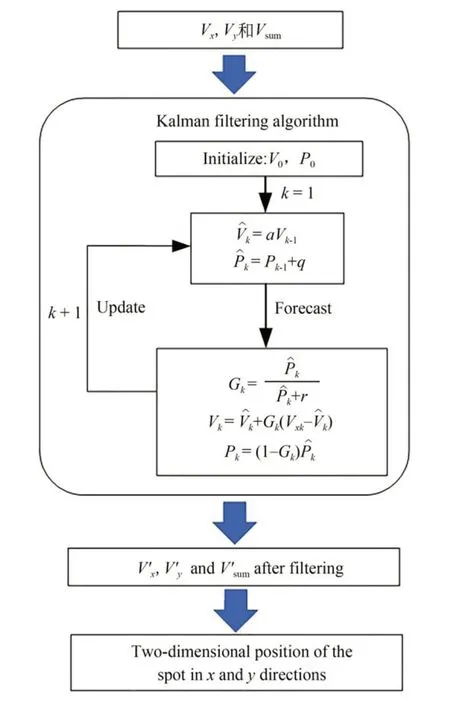
图1 卡尔曼滤波流程框图Fig.1 Block diagram of Kalman filter flow

2.2 位置电压信号卡尔曼滤波降噪仿真

由于PSD 三个代表位置的信号端口输出的是直流电压信号，实际进行AD 采样时这些端口的位置信号呈现幅值再叠加含高斯白噪声信号，当光斑位置改变时，幅值也跟着改变。为了验证卡尔曼滤波降噪算法的可行性，使用MATLAB软件进行位置电压信号卡尔曼滤波降噪仿真。以其中一个端口电压信号为例，如图2（a）所示，选择实验时真实采集到的有用信号恒为0.4 V 的直流电压信号为理想信号，一段时间后该理想位置电压信号变为0.25 V。选择均值为0，在±1.5 mV 均匀随机分布的高斯白噪声作为噪声信号，如图2（b）所示，理想信号和高斯白噪声叠加作为仿真输入信号。设置滤波器迭代10 000次，过程噪声协方差q值取10-6，测量噪声协方差r值取0.05，仿真结果如图2（c）和图2（d）所示。

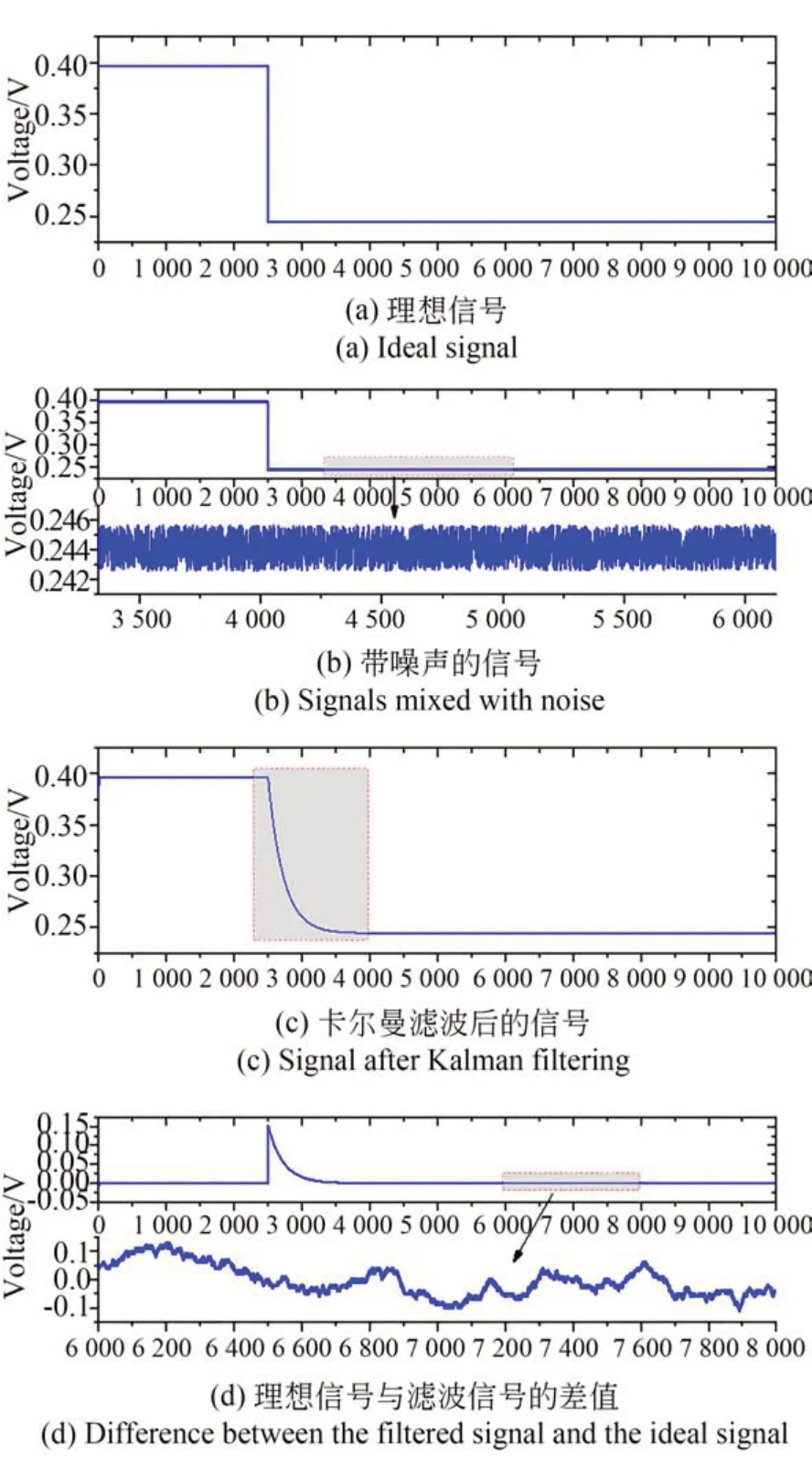
图2 卡尔曼滤波仿真效果Fig.2 Kalman filter simulation effect

图2 （c）是卡尔曼滤波后信号仿真结果，可以看出卡尔曼滤波过程需要1 500 次迭代，但若算法在FPGA+ARM 架构上实现，运算速度能达到10 MHz 以上，意味着最多0.15 ms 延迟完成滤波，可满足光斑位置变化的测量要求。图2（d）是滤波信号与理想信号差值的仿真结果，稳定后的滤波信号与理想信号差值从±1.5 mV 降到±0.14 mV，输出的电压信号中毛刺大幅减小。仿真结果表明，卡尔曼滤波具有较好的降噪效果，经过电压与光斑位置换算关系进行运算后，能够实时得到更为准确的PSD 光斑位置信息。

3 激光外差干涉位移测量及角度补偿系统

激光外差干涉位移测量及角度补偿系统装置如图3 所示。He-Ne 激光器发出两正交偏振且不同频率的光，经PBS 反射的s偏振光经过1/4波片QWP1和平面反射镜MR1反射，再经过QWP1后变成p偏振光作为参考光，而从PBS 透射的p偏振光依次经过QWP2和MR2反射，再次经过QWP2后变成s偏振光并作为测量光。测量光和参考光经过BS 分为两路，一路经过与两偏振方向呈45°偏振片P2后在光电探测器PD 处形成干涉信号；另一路经过偏振片P1滤除掉参考光后，入射到位置敏感探测器PSD 上作为角度测量光。假设作为移动测量镜的MR2移动的距离为S，探测器PD 处干涉信号的相位也发生变化，通过对干涉信号相位进行解调可以得到移动距离：

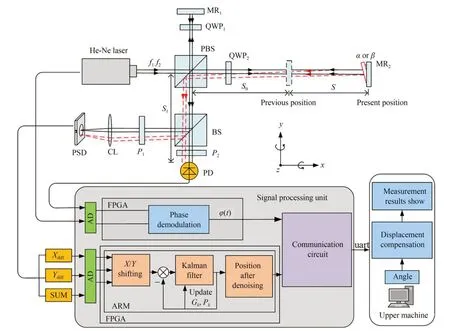
图3 激光外差干涉位移测量及角度补偿系统Fig.3 Laser heterodyne interferometric displacement measurement and angle compensation system

实际上，测量镜MR2在移动过程中会随着被测物体偏转而产生转角。从图3 中可以看到，MR2偏转使得反射测量光的路径和光程发生变化，带来位移测量误差。测量镜产生的转角能够体现在激光光斑位置在PSD 探测面的变化上，通过分析激光光斑位置的变化可以算出转角，再根据转角与位移补偿模型对位移进行补偿。

由于平面反射镜的特性，滚转角带来的位移测量误差影响可以忽略，因此这里主要对俯仰角和偏摆角进行测量。平面反射镜会产生偏摆角β和俯仰角α。以产生偏摆角为例，如图3 所示，光束在水平和竖直方向分别产生2β和2α的角度偏移，最终经过凸透镜后在位置敏感探测器PSD 汇聚成一个光点，由PSD 探测到激光光斑在两个方向的偏移量∆xPSD和∆yPSD，求得俯仰角和偏摆角为：

式中：∆xPSD是激光光斑在水平方向的偏移量，∆yPSD是激光光斑在竖直方向的偏移量，f是凸透镜的焦距。根据几何关系［22］可推出位移补偿公式为：

式中：S0表示PBS 和MR2之间的距离，S1表示PBS 和PD 之间的距离，S表示补偿前系统测得的移动测量镜的位移，S′表示补偿后系统测得的移动测量镜的位移，Hz表示激光光斑中心到y轴的距离，Hy表示激光光斑中心到z轴的距离。

4 实验及结果分析

为验证本文位移测量及角度补偿效果，实验搭建了激光外差干涉测量装置，如图4 所示。它包括双频激光器、偏振分光镜、四分之一波片、平面反射镜、偏振片、凸透镜、光电探测器和位置敏感探测器。其中，双频激光器采用美国Agilent公司的5517D 型激光器，波长为632.991 37 nm，位置敏感探测器采用美国索雷博公司的PDP90A 探测器，光电探测器采用美国索雷博公司的PDA36A2 探测器。

图4 激光外差干涉位移测量补偿装置Fig.4 Compensation devices of laser heterodyne interference displacement measurement

为实现位移与转角的同时测量，采用上海宇志通信公司的MFSS6842 信号处理板进行位移测量信号处理，AD 采样速度最高可达125 MHz，输入电压为±5 V，14 位分辨率，满足位移干涉信号的采集和信号处理要求；采用上海芯驿电子科技有限公司AX7Z010 开发板及AD7606 模块负责位置敏感探测器PSD 信号的AD 采集和处理，AD 采样速度最高可达200 kS/S，输入电压为±5 V，16 位分辨率，采集精度能够达到0.15 mV，能够准确测量PSD 位置电压信号；最后，将两块信号处理板处理后得到相位和滤波后直流电压值上传到LabVIEW 上位机，在上位机进行运算得到位移、转角测量结果及补偿后的位移测量结果。

4.1 光斑位置稳定性测量实验

为验证所设计去噪算法的可行性，首先进行了光斑位置稳定性测试实验。将测量平面反射镜安装在美国Thorlabs 公司的六自由度转台MAX606M 上跟随转台转动，转台转动5×10-4°后静止，记录15 s 未去噪处理的原始光斑位置、卡尔曼滤波后的光斑位置以及索雷博自带去噪算法得到的光斑位置，然后转台再进行转角运动如此反复记录多组数据，对这3 组不同算法下得到的光斑位置数据进行对比。以y方向激光光斑位置测量为例，稳定性测量实验结果如图5所示。

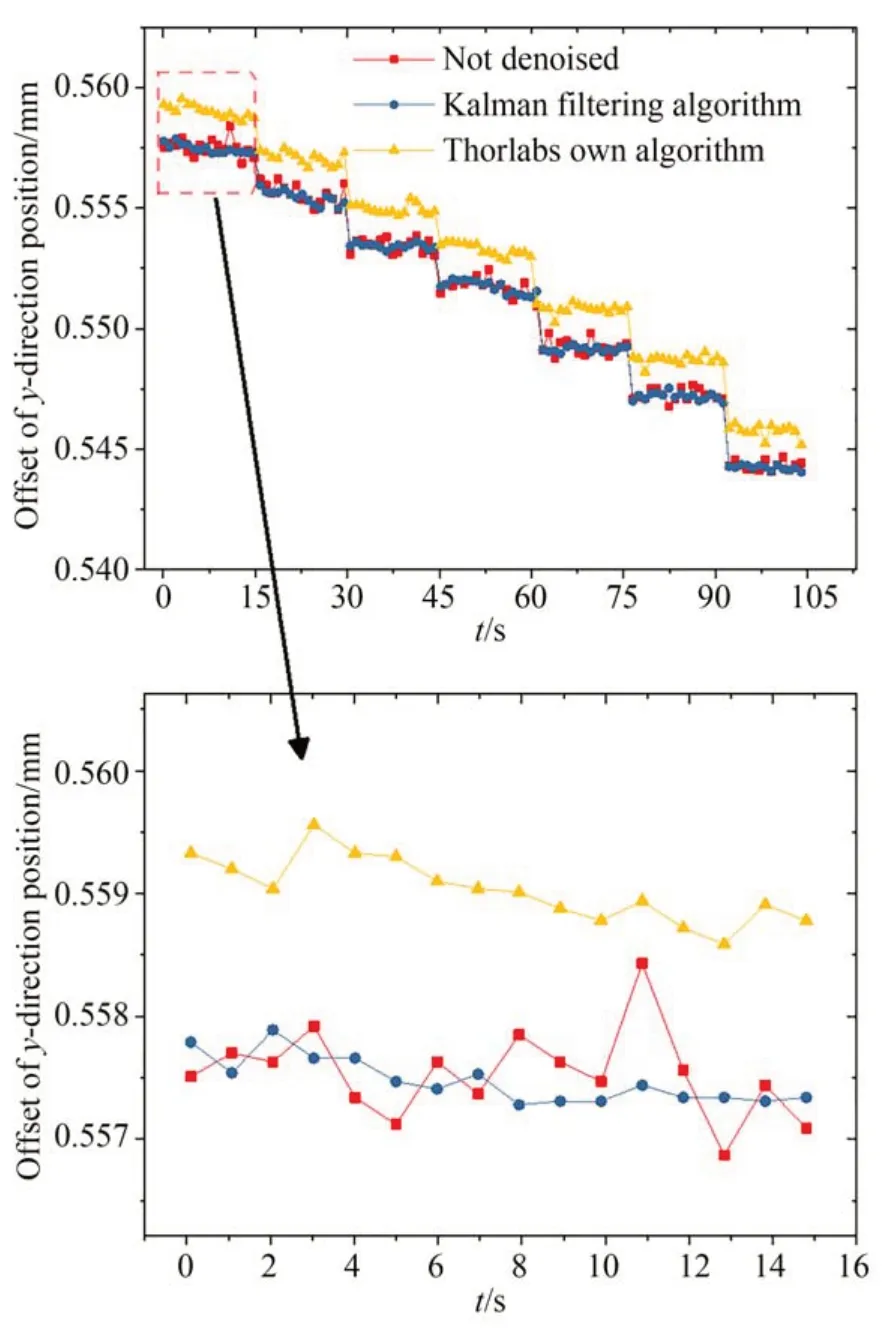
图5 光斑位置稳定性测量实验结果Fig.5 Experimental results of spot position stability measurement

从图5 中数据可以看到，FPGA 得到的原始未去噪处理的光斑位置、卡尔曼滤波后的光斑位置与索雷博自带去噪算法得到的光斑位置存在一定偏差，但相对位置的变化趋势是一致的，根据式（13）和式（14），转角测量需要测得的是光斑位置的相对变化量，这验证了卡尔曼滤波算法可用于转角的测量。截取第一段数据放大进行显示，索雷博去噪算法得到的光斑位置最大抖动偏差为0.8 μm，最小抖动偏差为-0.4 μm，抖动标准差为0.23 μm。未去噪处理的原始光斑位置抖动较为明显，最大抖动偏差达到了2.5 μm，最小抖动偏差为-1.58 μm，抖动标准差为0.52 μm，而经卡尔曼滤波后光斑位置的最大抖动偏差为0.5 μm，最小抖动偏差为-0.3 μm，抖动标准差降至0.18 μm。由此可知，卡尔曼滤波算法可以有效降低位置敏感探测器的测量噪声。

4.2 角度测量验证实验

为了验证角度测量的准确性，同样将测量平面反射镜安装在美国Thorlabs 公司的六自由度平台MAX606M 上跟随平台转动，该平台的转角精度为1.031 4×10-6°（0.018 μrad）。以俯仰角测量为例，控制MAX606M 依次做5 次俯仰运动，每次俯仰0.005°，将测量得到的角度跟索雷博六自由度平台的转角进行比较，实验结果如图6 所示。

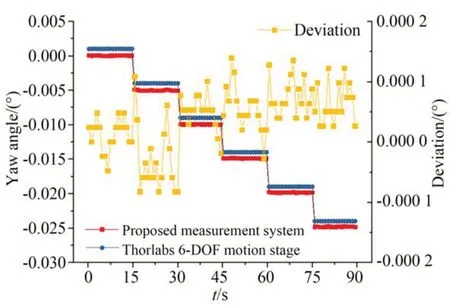
图6 角度测量对比实验结果Fig.6 Experimental results for comparison of angle measurement

为显示清晰，图6 蓝色的六自由度转台转角曲线上移0.001°。从图6 可以看出，测量系统卡尔曼滤波算法的延迟较小，具有较好的实时性，滤波后光斑位置稳定性好，测得转角数据与索雷博六自由度转台的转角数据偏差在±1.38×10-4°内，符合角度测量精度要求。角度测量结果表明，该系统满足角度测量的精度要求，可以对激光外差干涉位移测量进行补偿。

4.3 激光外差干涉位移测量补偿实验

为验证实际位移测量的补偿效果，以分辨率为0.1 μm 的德国PI 公司的M-531.DD 导轨为测量对象，将测量平面反射镜固定安装在M-531.DD 导轨起始位置上，M-531. DD 导轨起始位置距离激光器50 cm。转角引入的位移量与测量镜平面反射镜的转动支点位置有关，这里测量镜转动支点与导轨安装平台中心x轴方向的距离为1 cm，与导轨安装平台中心y轴方向的距离为0.8 cm。

实验时，控制导轨以1 mm/s 运动速度步进，每次步进后记录测量位移和测量转角，一共步进200 次，总移动位移为200 mm。系统测得俯仰和偏摆角度测量结果如图7 所示，位移补偿前后对比测量结果如图8 所示。

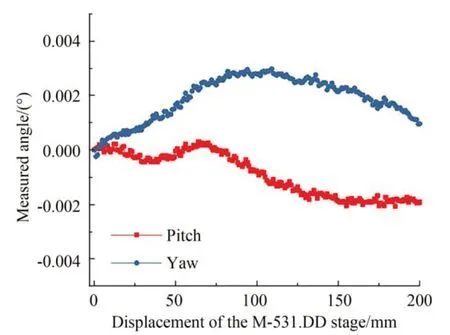
图7 激光外差干涉位移测量系统测得的测量镜转角Fig.7 Angle of measuring mirror measured by laser heterodyne interferometric displacement measuring system

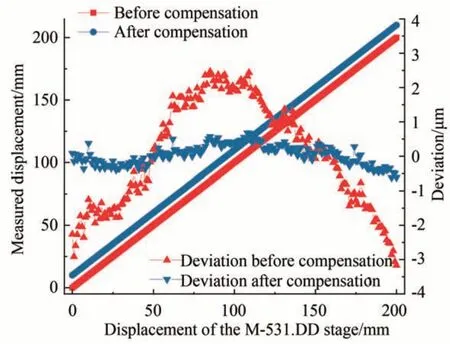
图8 位移补偿前后对比Fig.8 Comparison before and after displacement compensation

由图7 可以看出，测量镜在M-531.DD 线性导轨的0~200 mm 行程内，偏摆角最大为2.97×10-4°，最小为 -2.072×10-3°，俯仰角最大为2.986×10-3°，最小为-2.44×10-4°。为方便观察，将补偿后的位移测量数据向上整体平移10 mm。由图8 可以看出，补偿前位移测量结果与M-531. DD 线性导轨的位移数据趋势不一致，其偏差结果呈现出“抛物线”曲线，最大偏差为2.39 μm，最小偏差为-3.16 μm，标准差为1.55 μm；补偿后位移测量数据与M-531.DD 线性导轨位移数据的最大偏差降至0.68 μm，最小偏差降至-0.61 μm，标准差降至0.29 μm，验证了本文位移补偿方法的有效性。

5 结 论

本文针对激光外差干涉仪在测量过程中由被测对象转角引入位移测量误差的问题，提出了一种激光外差干涉仪转角误差测量及位移补偿的方法，通过FPGA+ARM 架构对位置敏感探测器信号进行采集，使用卡尔曼滤波算法对光斑位置信号进行去噪，提高光斑位置的测量精度，得到更为准确的转角测量结果，最后根据补偿模型对位移进行补偿。为验证转角测量及补偿方法的可行性，进行了光斑位置稳定性、角度测量精度、位移测量及补偿实验。实验结果表明，所提出的卡尔曼滤波方法能够有效减小位置敏感探测器的噪声误差，最大抖动偏差从2.5 μm 减小到0.5 μm，最小偏差从-1.58 μm 减小到-0.3 μm，抖动标准差从0.52 μm 减小到0.18 μm；系统测量的角度与索雷博六自由度转台的转角偏差在±1.38×10-4°内；经过位移补偿，位移测量结果与M-531. DD 导轨定位数据的最大偏差从2.39 μm 减小到0.68 μm，最小偏差从-3.16 μm 变到-0.61 μm，标准差从1.55 μm 减小到0.29 μm，有效补偿了测量镜在移动过程中转角带来的位移测量误差，提高了位移测量精度，可应用于微纳米测量等领域。