悬吊式重力卸荷系统的主动式缓冲控制

晏慧星， 卢鸿谦， 尹 航， 黄显林， 陈泰年

（哈尔滨工业大学 控制理论与制导研究中心，黑龙江 哈尔滨 150001）

1 引 言

我国正在开展地外天体采样、巡视探测、宇航员着陆等航天任务，由于复杂的地表与重力环境，地面微/低重力试验系统是总体方案设计与性能测试的重要手段，其中的关键是重力卸荷问题。目前，地面微/低重力试验系统中应用较多的是梁索结构的悬吊式重力卸荷平台［1］。为了实现高性能重力卸荷实验，该平台需要实现两个目标：一是吊索补偿力恒等于实验对象全部或部分重力；二是二维随动平台需要保证吊索补偿力水平分量尽可能为零。本文重点关注该平台第一个目标的实现。由于吊索力容易出现冲击突变，外加航天器刚度偏低存在挠性，现有的悬吊式索驱恒拉力系统多数引入弹性缓冲器（弹簧等）抑制力冲击，减小力误差。但是柔性缓冲器的引入降低了系统带宽，使得力矩电机对扰动抑制能力下降，并且引入被动缓冲器使索驱悬吊式系统成为欠驱动系统［2］。这大大增加了重力卸荷控制的难度，给实现精确力跟随控制带来了挑战。

目前，在不同应用场景中，关于刚性驱动+弹性缓冲环节的恒拉力技术成果比较丰富。国内外专家提出了一系列机构设计方案，有研究人员通过增加主动驱动源来解决被动弹性元件刚度受限的问题，采用电动推杆+缓冲弹簧构成一个主动弹性元件［3］，但是电动推杆需要在弹性元件被压缩后才去调节，存在明显的滞后现象。哈尔滨工业大学提出了一种旁路张紧式恒拉力机构［4］，该机构能够在一定的输出行程内保持输出力基本恒定，但存在结构复杂、质量体积偏大等问题。这些都没有从根本上解决被动弹簧引入的欠驱动问题。

近年来，气动人工肌肉以结构简单、材料轻便、柔顺性和安全性强等优点［5-7］，已经大量应用在航空航天、工业生产和医疗康复等领域。柔性特征能够使气动人工肌肉作为缓冲器，质量轻质能够极大地减小寄生质量问题。然而，气动人工肌肉与生俱来的迟滞、高度非线性、蠕变等特性，导致其精确控制难度很大。目前，大多数研究集中在位置跟踪控制，控制方法主要有PID 控制［8］、滑模控制［9］和非线性模型预测控制等。考虑到悬吊式重力卸荷系统中存在挠性、串震等问题，控制方法并不能简单移植其他领域相关方法。

模型预测控制（Model Predictive Control，MPC）在应对具有物理约束和多输入多输出复杂系统方面具有优越性［10］。MPC 将控制问题转化为二次规划问题，可以利用基于梯度的优化［11］和序列二次规划［12］等方法求解。然而，该方案的成功实施取决于精确的系统模型［13］，而对于复杂的非线性系统，要建立精确的模型往往是困难的。针对该问题，很多研究人员采用神经网络［14］、高斯过程［15］和模糊逼近［16］等策略，以便能够在线估计系统未建模的动态特性。

本文提出了采用PAM 作为重力卸荷系统的主动缓冲器，从根本上避免欠驱动问题，建立了基于PAM 的单吊索悬吊式重力卸荷系统的动力学模型。考虑到PAM 的非线性特性，采用级联式块结构的非线性神经网络，设计非线性模型预测控制器，实现了对PAM 的力跟踪控制，并且仿真实验和实物实验验证了本文提出的控制方法能够有效抑制扰动。本文的研究成果为后续悬吊式重力卸荷系统的主动缓冲器设计奠定了基础。

2 机构描述及动力学模型建立

首先介绍了梁式结构的悬吊式重力卸荷系统平台，针对单吊索悬吊式重力卸荷系统进行动力学建模，并且参考PAM 相关文献建立非线性PAM 动力学模型。

2.1 机构描述

常用的梁式结构的悬吊式重力卸荷系统是一种高效的重力卸荷技术，其总体结构如图1 所示。该系统包括二维随动子系统、悬架机构子系统、恒力控制子系统、位置传感器和缓冲器等。其中，二维随动子系统可以实现水平方向的运动，悬架机构子系统通过悬吊方式向实验目标提供一个反向力实现微/低重力卸荷，恒力控制子系统需要保持该反向力的稳定性。缓冲器则可以有效地抑制力冲击，降低吊索力误差。

图1 梁索结构的悬吊式重力卸荷系统平台示意图Fig.1 Schematic diagram of suspended gravity unloading system platform with beam-cable structure

2.2 单吊索悬吊式重力卸荷系统动力学建模

从常用的梁式结构的悬吊式重力卸荷系统出发，建立基于PAM 的单吊索悬吊式重力卸荷系统动力学模型，如图2 所示，图中变量定义如表1 所示。它由力矩电机、气动肌肉和力传感器组成。定义向上收绳为正方向，向下放绳为负方向，整个系统中x初始位置为零。

表1 各变量的物理含义解释说明Tab.1 Explanation of physical meanings of each variable

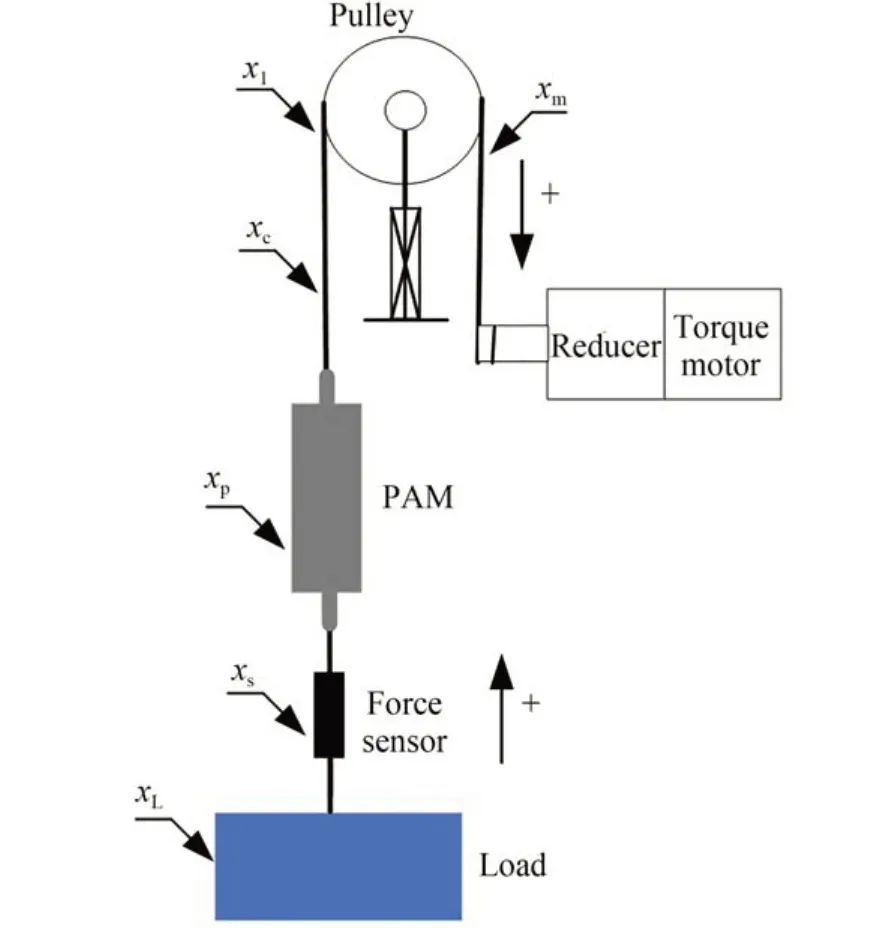
图2 单吊索悬吊式重力卸荷系统Fig.2 Single sling suspension gravity unloading system

滑轮转动的动力学方程为：

对钢丝绳采用集中质量法，利用线性分式变换（Linear Fraction Transformation，LFT），对悬吊式重力卸荷系统中确定部分和不确定部分分离建模得到：

其中：PAM 的弹性系数KP是实现主动缓冲器的关键参数。负载运动具有强不确定性，可近似建模为：

其中：G为工件重力；KL，ηL为被测工件支撑的弹性系数和阻尼，浮空时不起作用；KL=0 N/m，ηL=0 N·s/m，触地过程和行走过程为时变参数，最大值为KLmax和ηLmax。

2.3 非线性PAM 动力学建模

文献［17］提出PAM 产生的拉伸力取决于内层和外层的几何变化、材料参数，同时也取决于空气压力P，引入收缩参数κ为：

其中：l0是PAM 的初始长度，l是PAM 的实际长度。

文献［18］结合以往气动肌肉建模的研究成果，扩展之前的数学模型，形成了一个更加复杂的数学模型：

其中：F是气动肌肉产生的力，a1，a2，a3，a4，a5和a6是未知常数，e 是自然对数。

式（7）可以用于计算气动肌肉的相关参数，那么定压下气动肌肉的弹性系数为：

式中：m是气动肌肉下端悬吊重物，x是收缩长度是阻尼系数。

最后，用式（8）中的K̂P代替式（3）和式（4）。整个系统的输入控制量为力矩电机的速度uV和PAM 的气压uP，输出量是PAM 的实际力F(κ，P)，通过力传感器测量得出。

3 非线性模型预测力跟踪控制

3.1 PAM 非线性模型参数辨识

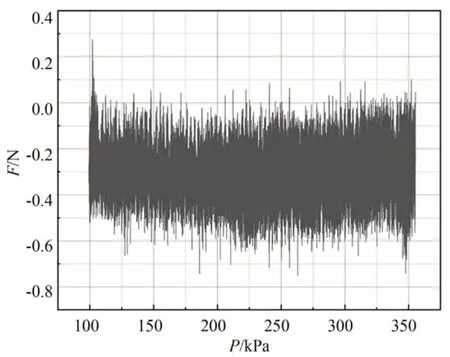
通过PAM 数据采集平台（如图8 所示）采集PAM 输入输出数据。运用多元非线性回归算法拟合非线性模型式（7），PAM 数据采集平台输出的实际力与非线性多元回归算法拟合力相减得到力误差，如图3 所示。在回归过程中，难以求得相应参数使得预测输出与实际输出之间的误差在10 N 以内。

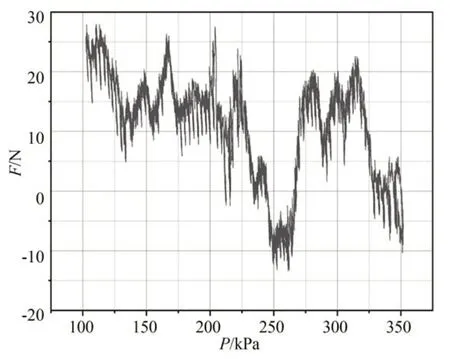
图3 非线性模型拟合力误差Fig.3 Nonlinear model fit force error

为了获取更加准确的预测模型，这里采用基于深度神经网络的数据驱动法来构建PAM 非线性动力学模型。然而，神经网络模型存在一个问题，即这些模型很难在未见的数据上表现出良好的性能，这可能导致不可靠预测数据［19］。

最后，本文提出了基于物理约束的PAM 系统辨识算法，进一步将经典系统辨识技术的优点与深度学习相结合，建立了非线性系统的模块化表示，其中包含可辨识的神经网络模块，这些模块可能受到结构先验的约束和影响。这种方法通过网络权重、状态和输入约束的特征值正则化以及其他的边界条件约束，来保证系统的稳定性。该方法由输入、状态和输出动态三部分神经网络块组成，可以限制网络权重和系统变量的变化范围［20］。

首先使用具有系统状态和输入动力学的结构化表示的公式进行先验假设。考虑大部分采用输入输出数据进行系统辨识，因此模块化非线性动力学模型采用离散形式，即：

其中：fx是系统动态的非线性映射，fu是系统控制的非线性映射，fy是系统输出的线性映射。

为了实现对部分可观测的动力学系统建模，假设状态xt表示潜在动力学模型，引入另一个神经网络来表示状态观测器：

其中：fo表示状态观测的非线性映射，yt是系统观测输出，ny表示被控对象输出时间序列的延迟阶次，其值可以通过系统辨识获得。

图4 中，每个块结构的神经网络都采用两层结构，每层神经网络包含16 个神经元，激活函数选用ReLu 函数。由于输入气压实际中是有界的，因此引入相应的约束限制输入动态fu，同时考虑PAM 的物理特性设置相应输出约束限制预测输出力f(y)。

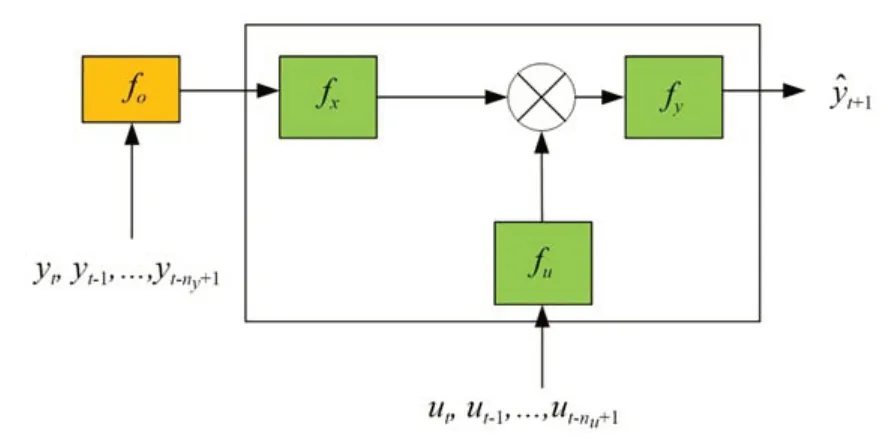
图4 一步预测块结构非线性神经网络模型Fig.4 One-step predictive block-structured nonlinear neural network model

这里采用级联神经网络实现多步预测，具体架构如图5 所示。为了能够实现在线训练块结构的神经网络，控制系统中采用一个用于存储输入输出数据的缓冲器。设置缓冲器存储满3 000 控制周期数据后，训练网络更新网络参数。更新网络参数后，缓冲器会被清空，以便存储新数据，并开始下一周期的训练过程。

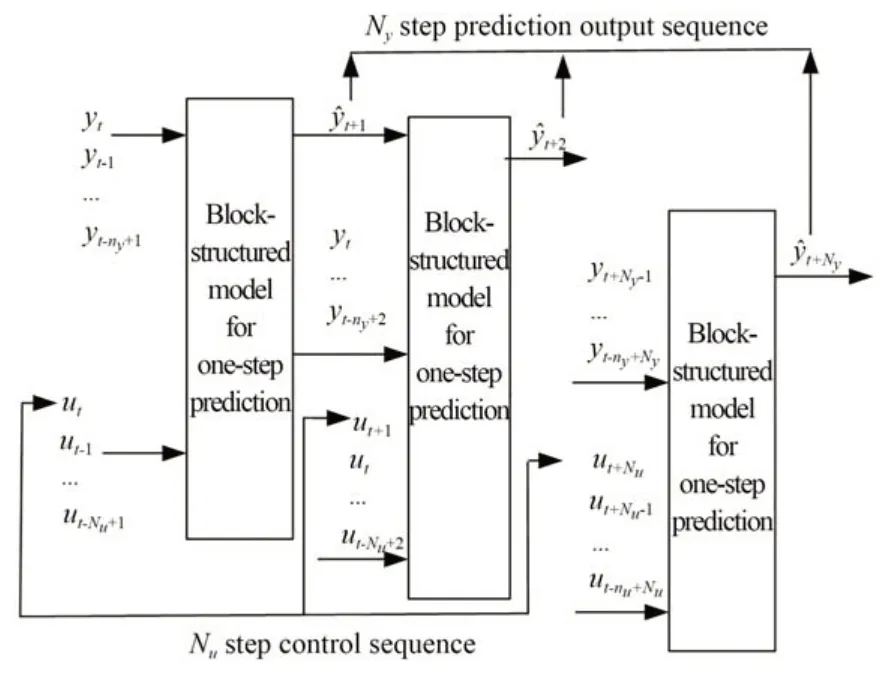
图5 级联的多步预测模型Fig.5 Cascaded multi-step prediction model

3.2 非线性模型预测力跟踪控制

3.2.1 单吊索重力卸荷系统控制原理

整个单吊索重力卸荷系统的控制系统框图如图6 所示。力矩电机工作在速度模式下，速度控制器通过Δxcs=xc-xs去调节速度控制律。控制框图中的重点是控制PAM 的MPC 控制器，它通过前一段时域的PAM 实际力Fs、实际气压P和实际长度l，去预测PAM 下一段时域的拉伸力，然后优化求解控制律。

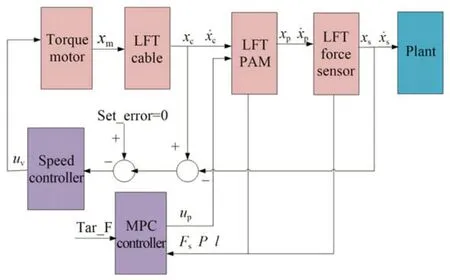
图6 单吊索重力卸荷系统的控制框图Fig.6 Control diagram of single-tether gravity unloading system

3.2.2 PAM 非线性模型预测力跟踪控制

NMPC 控制器主要包括两部分，一是预测部分，另一个是优化求解部分［14，21］。控制方案如图7 所示，模块化状态空间模型近似PAM 的动力学和预测未来行为，然后，将预测未来时刻输出与期望的轨迹一起输入优化控制器［22］，从而解决有限时域优化控制问题。图中，MPC 策略中优化部分采用CasADi 工具箱［23］进行求解。

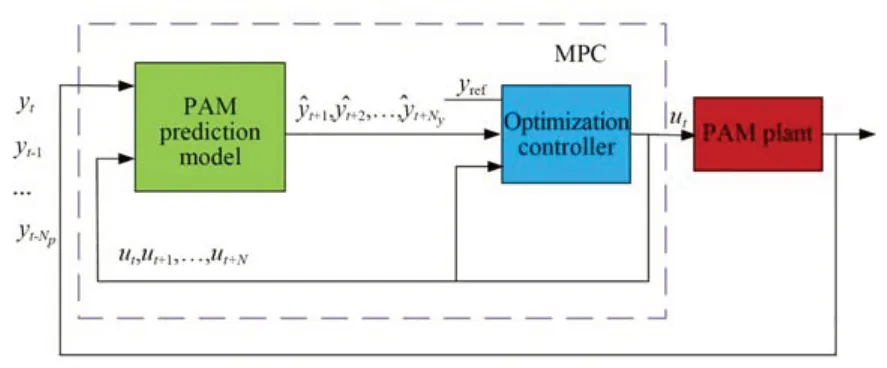
图7 PAM 非线性模型预测力跟踪控制Fig.7 PAM nonlinear model predictive force tracking control

仿真实验中，图（7）中PAM 对象模型采用式（7）建立模型，利用多元参数回归出式（7）常数a1，a2，a3，a4，a5和a6的值。

用于力跟踪模型预测控制的代价函数如下：

满足约束：

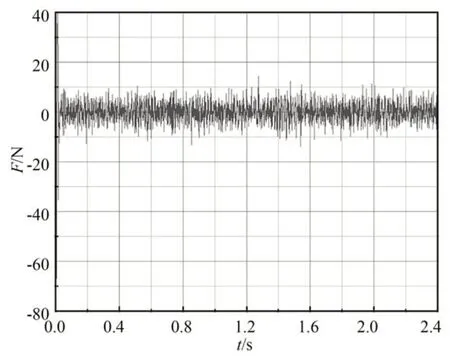
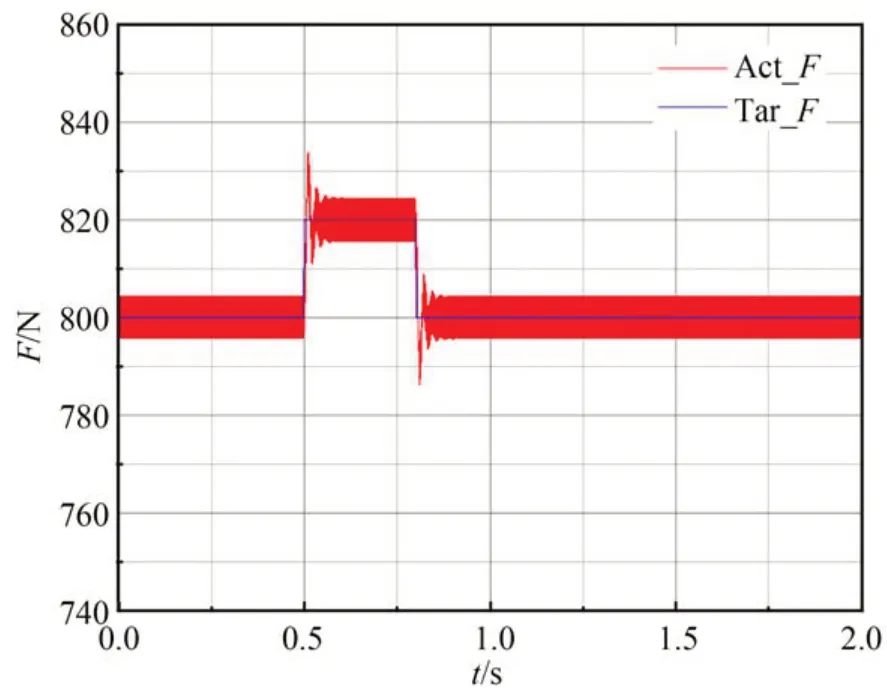
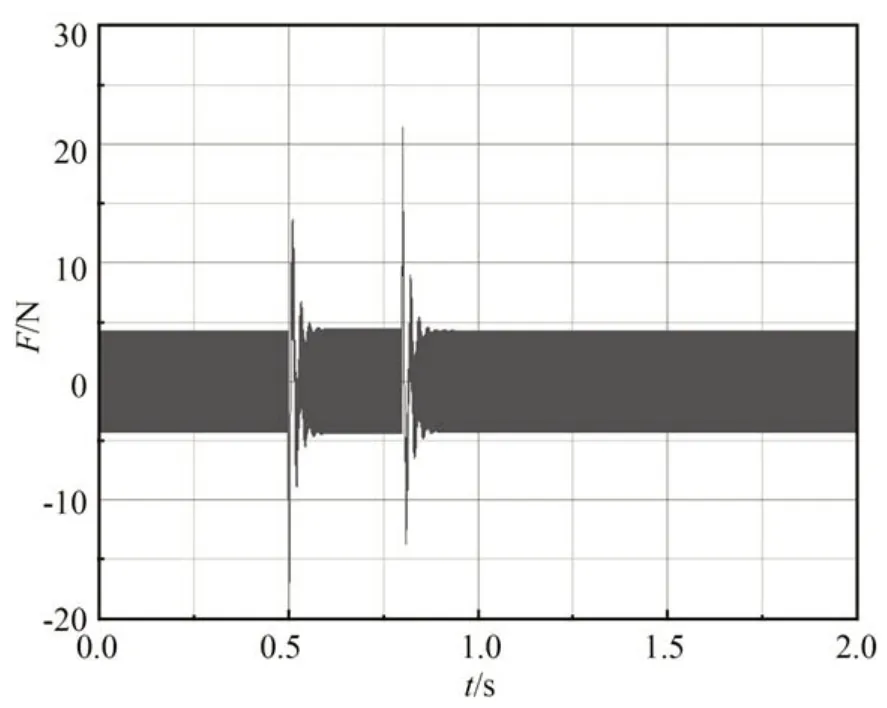
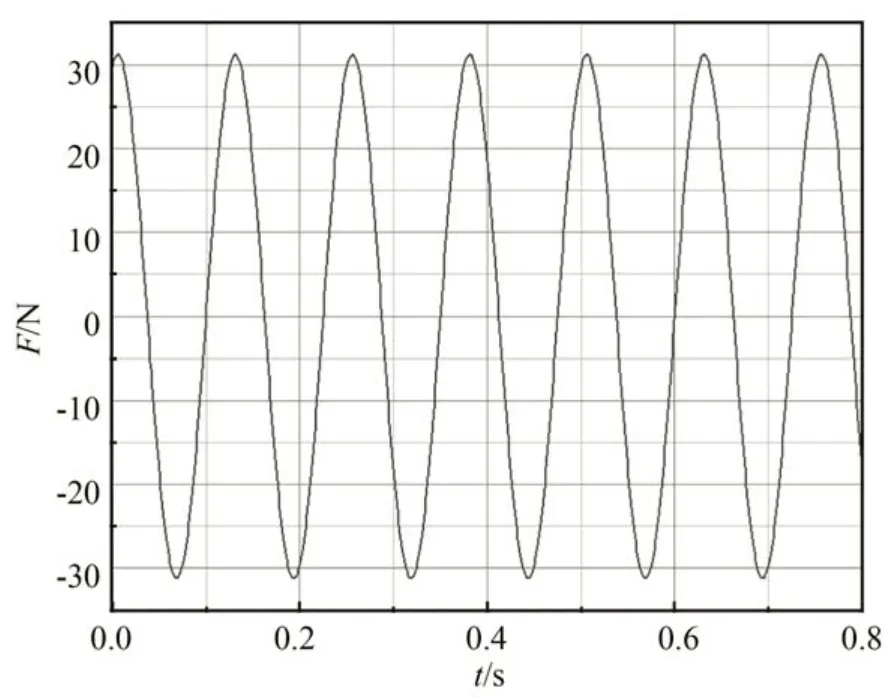
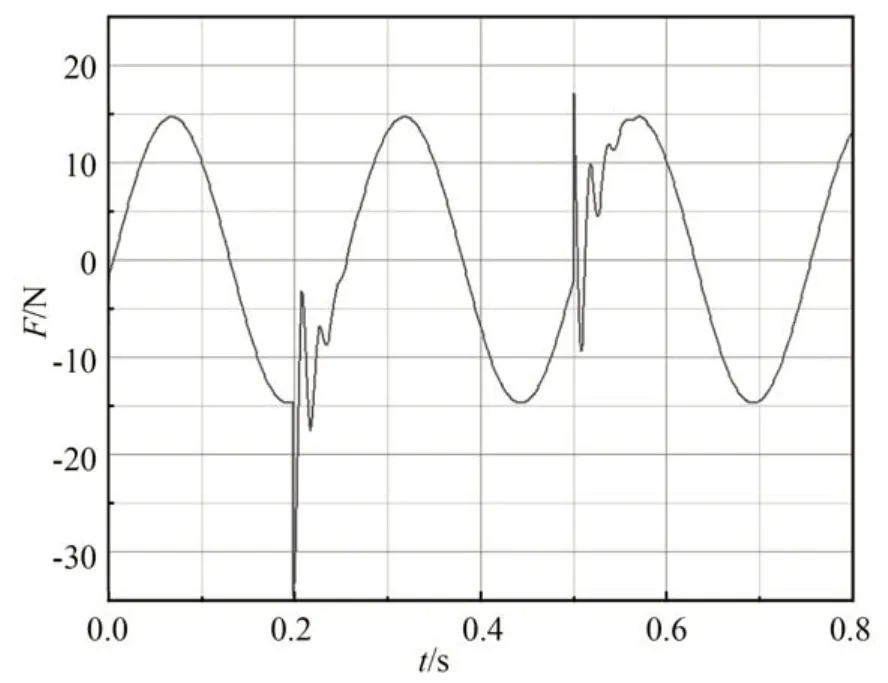
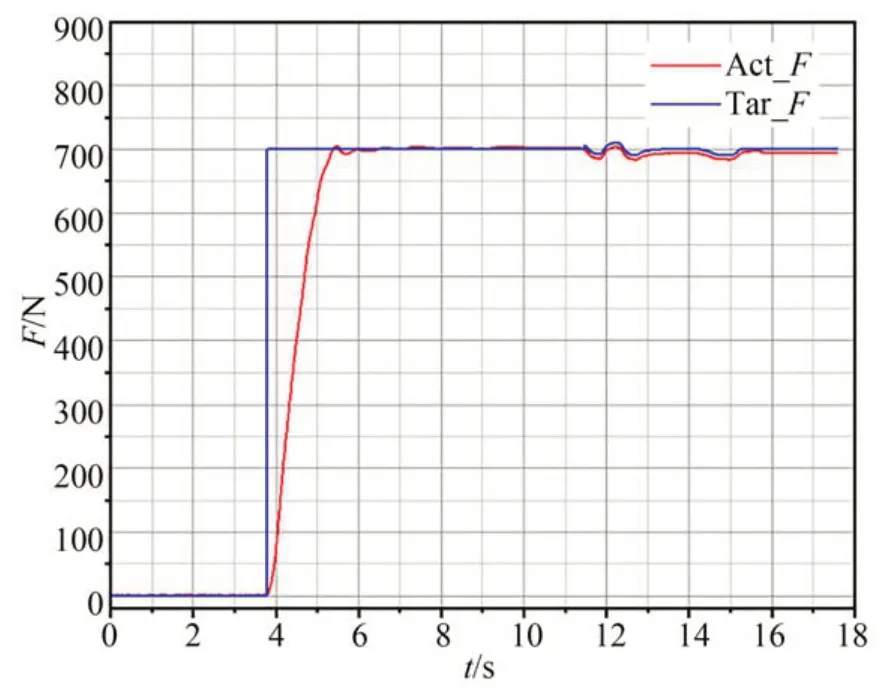
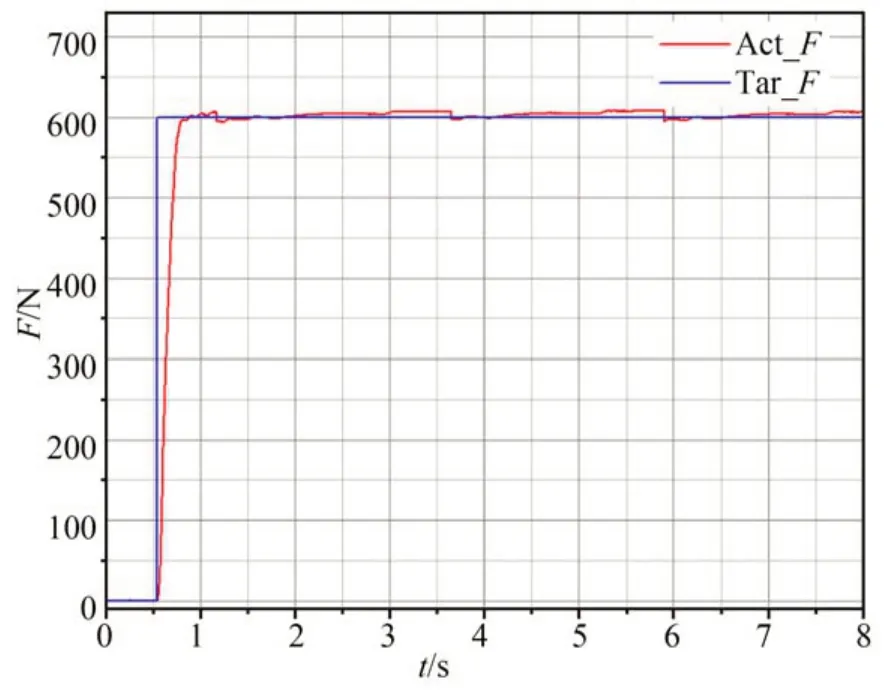
其中：e(t+k)=ŷ(t+k)-yr(t+k)，yr(t+k)为跟踪参考轨迹，uc(t)为控制信号，Δuc为增量控制信号，Np为预测时域（预测未来Np时刻PAM 输出的拉伸力），Nu控制时域（给出Nu-1时刻PAM 的控制量，实际只用ut控制PAM），其中Nu必须小于Np（Nu

4 仿真与实验

4.1 训练块结构的非线性神经网络模型

搭建的数据采集平台如图8 所示，它由气动肌肉、力传感器、位移传感器和气压传感器等组成。两根气动人工肌肉通过链条连接，其中气动人工肌肉A 作为模拟不同负载，不断改变气动人工肌肉B 的输入气压。尽可能采集不同气压、不同压缩率下的数据，用于块结构的非线性神经网络辨识。

图8 PAM 数据采集平台Fig.8 Experimental platform for PAM data sampling

采集数据以元组形式访问系统测量的有限集合，每个元组对应于沿着具有时间间隔ΔT的采样轨迹的输入输出数据对。

采用级联神经网络实现多步预测，首先利用输入输出数据对训练一步预测神经网络，将输入输出数据对分为训练集和测试集，将训练集进行小批次处理，打乱数据集的时序关系，采用梯度下降法优化网络参数，训练5 000 个回合后，误差收敛接近零。为了验证块结构的非线性神经网络模型的可靠性，将测试集输入数据作为网络模型输入，网络模型输出与测试集输出集相减，得出力误差如图9 所示。

图9 非线性神经网络模型预测的力误差Fig.9 Force error plot predicted by nonlinear neural network model

由网络模型预测结果与实际输出的误差，可以看出神经网络模型的预测精度远高于非线性模型式（7）。

4.2 基于块结构非线性模型预测跟踪力控制

仿真中设置PAM 末端悬挂800 N 重物，测试实现零重力，为了测试系统应对噪声的能力，增加均值为10 N 的高斯白噪声。PAM 输出实际力和期望轨迹力如图10 所示，跟踪力误差如图11 所示。

图10 引入高斯噪声的期望力和实际力的波形Fig.10 Expected and actual force plot for introducing Gaussian noise

图11 引入高斯噪声的跟踪力误差Fig.11 Force error plot for introducing Gaussian noise

为了测试主动缓冲器抑制扰动的能力，运行期间加入时长为0.3 s，幅值为20 N 的阶跃响应。PAM 输出实际力和期望轨迹力如图12 所示，跟踪力误差如图13 所示。

图12 跟踪冲击扰动的期望力和实际力波形Fig.12 Expected and actual force plot for tracking impact disturbance

图13 跟踪冲击扰动的力误差Fig.13 Force error plot for tracking impact disturbance

为了测试系统的控制响应情况，使用振幅为500 N，偏置为1 000 N，频率为8 Hz 的正弦信号。PAM 输出实际力和期望轨迹力如图14 所示，跟踪正弦信号的力误差如图15 所示。

图14 跟踪正弦信号的期望力和实际力的波形Fig.14 Expected and actual force plot for tracking sinusoidal signal

图15 跟踪正弦信号的力误差Fig.15 Force error plot for tracking sinusoidal signal

在振幅为500 N，偏置为1 000 N，频率为4 Hz 的正弦信号基础上，为了模拟系统受到的冲击响应，测试系统抑制扰动的能力。加入时长为0.3 s，幅值为20 N 的阶跃响应。PAM 的输出实际力和期望轨迹力如图16 所示，跟踪力误差如图17 所示。

图16 跟踪具有扰动正弦信号的期望力和实际力的波形Fig.16 Expected and actual force plot for tracking perturbed sinusoidal signal

图17 跟踪具有扰动正弦信号的力误差Fig.17 Force error plot for tracking perturbed sinusoidal signal

4.3 实物仿真实验

为了模拟微/低重力实验目标物离地场景，实验采用弹簧代替柔性负载。实验装置如图18所示，选择FASTO 公司生产的长度为500 mm、最大拉伸力为6 000 N 的PAM。为了确保实验的准确性，选用精度高达0.03%~0.05%的S 型拉力传感器，同时使用精度为0.01 mm 的激光传感器实时测量PAM 的长度变化。通过更换不同刚度的弹簧模拟不同柔性负载。

图18 PAM 力跟踪控制实验平台Fig.18 Experimental platform for PAM force tracking control

气动人工肌肉力控制实验测试如图19 所示。在12 s 左右加入不规则扰动，可以看出，非线性模型预测控制依然能够表现出良好的跟踪性能。

图19 跟踪实验中PAM 的期望力和实际力Fig.19 PAM expected and actual force in tracking experiment

考虑实际的安全性，启动时特地增加相应限制，所以图20 的过渡时间大于1 s。实际应用中一般都是提前给PAM 充入一定气压。为了测试实际的阶跃响应特性，设置期望的目标为600 N，阶跃响应过渡时间大概在0.3 s 左右。

图20 跟踪阶跃信号PAM 的期望力和实际力Fig.20 PAM expected and actual force plot for tracking step signal

5 结 论

本文提出采用基于PAM 的主动缓冲器去解决目前悬吊索重力卸荷系统（刚性驱动+被动弹簧缓冲）存在的欠驱动问题。针对高度非线性PAM 主动缓冲器控制的难题，提出了基于块结构的非线性神经网络模型预测跟踪力控制方法。仿真实验表明，该方法的预测误差能控制在1 N以内，能够跟踪8 Hz 正弦信号、阶跃扰动等，力跟踪误差在3%以内。实验表明，控制方法能够跟踪不规则的力信号。然而，实验也发现几个问题：MPC 优化求解有待提高；驱动PAM 存在一定慢响应问题；PAM 偶尔会出现激振现象。未来的研究重心将放在改进优化求解算法，以及解决PAM 慢响应和激振问题上。