海洋捕食者算法的改进及其应用①

王梦娴, 王慧明, 刘永明,, 赵转哲,,*, 刘志博

(1.安徽工程大学机械工程学院,安徽 芜湖 241000;2.黄山工业泵制造有限公司,安徽 黄山 242700;3.安徽工程大学人工智能学院,安徽 芜湖 241000)

0 引 言

工程优化问题在生产过程中非常常见, 传统的优化方法对处理现代越来越复杂的工程问题捉襟见肘,易陷入局部最优而导致求解精度不高。而采用元启发式智能优化算法进行求解,已成为一种趋势[1]。海洋捕食者算法(Marine Predators Algorithm, MPA)是Faramarzi等人受海洋中捕食者和猎物间的移动与生物相互作用中最佳遭遇率策略的启发而提出的新型群智能优化算法[2],具有参数较少、灵活性较高的特点,但在实际应用中,随着工程问题复杂性的增加,其易陷入局部最优的缺点会越来越突出,如文献[3]提出将种群分组并采用不同的搜索策略;文献[4]在处理图像分割问题时提出基于混沌映射的改进策略。

实际上,一方面,MPA以随机因素进行初始化,大大降低了优化效率和鲁棒性。在优化的中间阶段,种群行为转换灵活性欠佳。另一方面,若猎物觅食成功,算法会过早收敛。针对此,本文提出一种融合多种策略的海洋捕食者算法(Fused multi-strategy Marine Predator Algorithm,FMPA),并通过多个测试函数和工程优化案例验证算法的有效性。

1 基本海洋捕食者算法

MPA是一种模拟海洋中捕食者觅食猎物运动策略的优化算法,捕食者根据莱维和布朗的交替运动将整个算法分为三个阶段[2]。

阶段1:探索阶段,猎物移动速度比捕食者快,捕食者最优策略为完全不动,猎物服从布朗运动,数学模型如式(1):

式(1)中:Si为移动步长;RB为基于布朗运动的随机向量;Rv∈(0,1)是均匀随机向量;t为当前迭代次数;T为最大迭代次数。

阶段2:探索转开发阶段,猎物的速度和捕食者一样,一半捕食者进行莱维运动来开发,另一半负责布朗运动的探索,公式如式(2),式(3):

阶段3:开发阶段,捕食者速度比猎物要快,其数学模型为式(4):

为避开局部最优值的停滞,算法考虑了环境因素影响如鱼类聚集装(FADs),数学模型为式(5):

Preyi=

(5)

式(5)中,U为随机二进制向量;Preyri(i=1,2)为随机猎物。

2 融合多种策略的海洋捕食者算法(FMPA)

2.1 折射反向学习

反向学习是改善种群初始化的常用手段,但其灵活性低使得算法后期容易在局部最优值停滞,故在反向学习策略中融入光的折射原理得到折射反向学习策略,其原理如图1所示[1]。

图1 折射反向学习原理图

其中,[l,u]为搜索范围,O为中点,入射、折射光线的对应长度为h,h*,入射角和折射角为α,β,由图1中线段的几何关系可得折射率z:

(6)

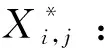
(7)

2.2 正余弦算法

正余弦算法是一种利用正弦和余弦函数的振荡特性找到最优解的算法[5]。本文将其引入MPA算法,其位置更新公式如式(8):

Xi=

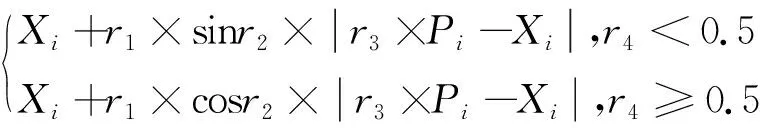
式(8)中,r1=1-t/T,r2∈[0,2π],r3∈[0,2],r4∈[0,1],Pi为当前最优个体的位置。r1控制算法在探索和开发之间的平衡,但线性递减函数不够灵活,选择文献[6]中的非线性递减函数表达式。

2.3 高斯-柯西变异

高斯分布和柯西分布属于连续概率分布,其中柯西分布两端较高,可增强算法的随机性。高斯分布中间高,针对小步长搜索能够提高搜索效率和精度[7]。本文将高斯-柯西分布引入,形成整个种群位置更新公式如式(9):

式(9)中,R3∈(0,1)是均匀随机数;C(1,0)是基于柯西分布的随机变量,G(1,0)是基于高斯分布的随机变量。

2.4 FMPA算法流程

在算法中引入折射反向学习初始化,在第二阶段加入正余弦算子,将高斯-柯西变异算子融入其中,生成新算法,FMPA流程图如下,

3 实验仿真与结果分析

实验的仿真环境为:Intel(R) Core(TM) i5-6200U CPU和MATLAB R2018b。使用多组标准测试函数来评估FMPA的性能,对所提出的新算法及基本MPA、基于准对立学习和Q学习的海洋捕食者算法(QQLMPA)、鲸鱼优化算法(WOA)和鹈鹕优化算法(POA)进行实验比较。参数设置参考原文献,种群数量为30,最大迭代次数为500,表1为5种算法独立运行30次的数据。

表1 基准函数结果对比

根据表1和图3的实验结果,可以看出FMPA在F1,F2和F5上的平均值和标准差都能达到理论最优值,收敛图像中改进算法在150次迭代前就收敛,表明FMPA的收敛速度快和鲁棒性好。在F3和F4中,虽然几个算法都达到了最优值,但由图2可知FMPA到达理想值的速度更快。F6图像为最优值之外有两个圆形尖峰即局部最优,FMPA可快速找到最优点,这表明新算法解决复杂优化问题的潜力。

4 FMPA在工程优化中的应用

为验证新算法的可行性,将FMPA应用到焊接梁和压力容器的设计,目标函数等信息见文献[8],种群数量为5,最大迭代次数为100。

4.1 焊接梁设计问题

目的是降低焊接梁的成本。变量为焊缝的厚度(x1)、棒的长度(x2)、高度(x3)和梁的厚度(x4)。

表2 焊接梁设计问题的结果比较

表2显示了使用5种算法获得的结果比较。根据结果,FMPA找到的最优值优于所有其他算法,提供的结果更符合实际需要。

4.2 压力容器设计问题

问题在于尽量降低压力容器的总成本。优化变量为壳体的厚度(x1)、头部的厚度(x2)、内半径(x3)和容器的圆柱截面长度(x4)。

表3 压力容器设计问题的结果比较

从表3中可看出,新算法为压力容器设计问题提供了优于其它智能算法的求解结果,也进一步表明FMPA的全局搜索性能更好。

图4 函数收敛曲线

5 结 语

(1)将折射反向学习、正弦-余弦算法和高斯-柯西变异多策略引入海洋捕食者算法,增加了种群的多样性,容易跳出局部最优,标准测试函数结果证明,可以有效地提高算法的收敛性能;(2)新算法在实际的多约束工程优化实例中成功应用,可以为其它类似问题提供一个借鉴方法。