SMA限位对铁路自复位桥墩地震反应的影响

罗 辉，夏修身，陈琦璠，黎大玮，张永强，马健行

(兰州交通大学土木工程学院,兰州 730070)

引言

桥墩与基础采用分离设计,在地震作用下,桥墩通过摇摆降低侧向刚度,延长结构自振周期来达到隔震目的,震后靠自重实现自复位[1]。自复位桥墩强震中不会再产生塑性铰区,避免桥墩产生严重破坏,可以确保震后结构的完整性,有助于快速恢复桥梁的使用功能。

最早开展结构摇摆研究的是Housner[2],Palermo等[3]开展了自复位桥梁墩柱节点的拟静力试验和非线性分析,并将单自由度推广到了多自由度的整桥简化模型。何铭华等[4]对自复位桥墩进一步完善和深化,从减小残余应变、增加回复能力出发,提出一种新型自复位墩柱节点体系。夏修身等[5-8]先后提出两弹簧模型和考虑限位装置的三弹簧模型,给出了提离弹簧的恢复力模型与刚度取值方法,进行分析模型的试验验证,探讨限位装置对自复位桥墩摇摆反应的影响。黄麟和郭展[9-10]设计了增设高阻尼橡胶垫块与自复位弹簧的自复位桥墩模型,进行振动台试验,与增设自复位弹簧的自复位桥墩相比,高阻尼垫块降低了自复位桥墩的加速度和应力响应,有效控制墩顶水平位移。杜骞等[11]研究了自复位桥墩在近、远场地震动高阶反应,结果表明:结构第2阶振型受近场地震作用的影响显著,远场地震动作用下墩顶水平位移更大。张哲熹等[12]研究了采用SMA拉索的摇摆自复位桥墩,讨论了桥墩的滞回曲线和复位能力,研究表明:与传统梁桥相比,采用SMA拉索桥墩可以有效降低结构残余变形以及桥墩本身的损伤。申彦利等[13]建立了新型装配式自复位桥墩节点的数值模型,相比传统桥墩节点,自复位桥墩节点的承载力和耗能能力有所提升,残余位移减小。贾俊峰等[14]建立了自复位预制拼装RC桥墩的数值模型,探讨了桥墩高宽比、预应力筋面积和初始张拉力等参数对自复位桥墩的影响。魏博等[15]研究了外置耗能器对自复位预制RC桥墩抗震性能的影响,结果表明:外置耗能器耗能段均出现明显的高阶屈曲形态,耗能作用明显。李帆等[16]开展了外置分阶段耗能阻尼器的自复位桥墩,与内置耗能钢筋自复位桥墩相比,外置分阶段耗能阻尼器自复位桥墩提高了桥墩水平承载力和桥墩初始刚度。自复位桥墩摇摆隔震效果好且稳定,但摇摆隔震可能会显著增大墩顶位移,限位装置可以减少墩顶位移;常规的预应力钢筋限位会明显增大墩底的地震弯矩,减弱自复位桥墩的隔震效果[5],且非弹性变形能力相对较弱。

SMA(形状记忆合金)具有变形能力大、耗能能力强及自复位能力好的特点[17-18]。尝试采用SMA进行自复位桥墩限位,并对SMA限位对自复位桥墩的影响开展系统研究。提出SMA限位单元模型,基于OpenSees建立自复位桥墩模型,探讨限位位置的初始间隙和初始预加力对自复位桥墩地震反应的影响,并和预应力钢筋限位效果进行对比。

1 基本分析数据

某单线普速铁路桥梁,其上部采用简支箱梁形式,桥梁计算跨径32 m,下部结构为群桩基础空心桥墩,其截面形式为圆端形,如图1所示。18号墩高58 m,高墩桥梁摇摆隔震效果好且稳定,为研究SMA限位对桥墩的影响,选取18号桥墩为研究对象,墩底扩大基础尺寸为10 m×12 m×3 m,宽度B=10 m,截面积A0=120 m2。顺桥向设计时桥墩及墩底扩大基础材料采用C30混凝土,其余参数详见文献[19]。

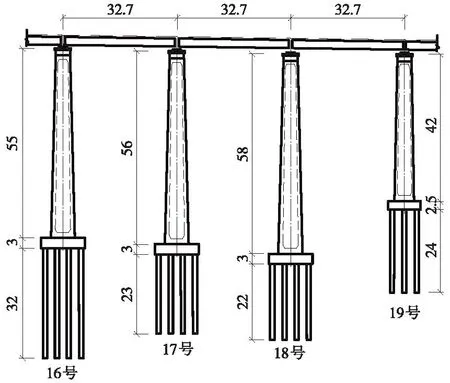
图1 某铁路桥墩桥梁立面布置(单位:m)Fig.1 Elevation layout of piers of a railway bridge (unit: m)

图2中左右两侧各布置4个φ32 mm的SMA限位拉杆,每侧面积A=0.003 2 m2,每根SMA拉杆长度为3 m。预应力筋限位见图2,将SMA拉杆替换为预应力筋。

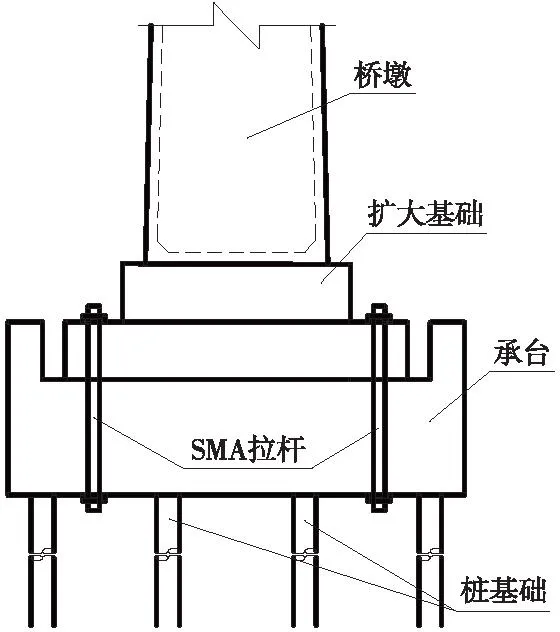
图2 SMA限位自复位桥墩Fig.2 SMA restrainer self-centering pier

2 有限元数值分析模型

SMA限位的自复位桥墩分析模型如图3所示。其中,墩柱、桥跨质量和桥墩的提离模拟采用文献[6]中模拟方法。以弹性梁单元element elasticBeamColumn模拟墩柱,刚臂单元模拟墩底扩大基础,刚臂的刚度取单元最大刚度的100倍。强震作用下,桥墩与承台分离,发生摇摆隔震,从而墩底提离。只受压弹簧模拟桥墩的提离,零长度单元 element zeroLength 模拟提离弹簧,模拟材料本构关系采用弹性只受压材料uniaxialMaterial ENT,根据文献[20],墩底提离弹簧刚度取k=2.1×108kN/m,SMA拉杆采用Self-Centering材料本构关系[21],见图4,采用桁架单元模拟。

图3 SMA限位的自复位桥墩分析模型Fig.3 Self-centering pier analysis model with SMA restrainer

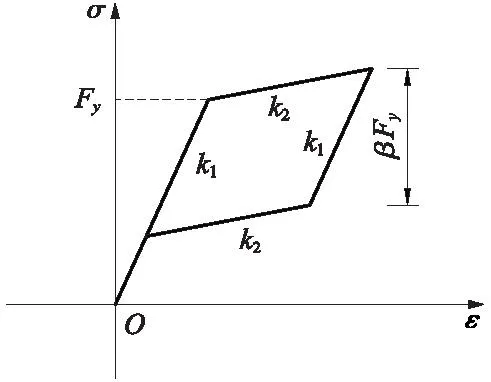
图4 SMA材料本构关系Fig.4 Constitutive relationship of SMA material

3 初始间隙对地震反应的影响分析

为探讨初始间隙δ对桥墩地震反应的影响,分别设置0,10,20,30,40 mm五组初始间隙进行分析。材料本构采用uniaxialMaterial ElasticPPGap。考虑初始间隙的SMA杆的布置、刚臂单元、零长度单元模拟方法与前文相同。

目前在OpenSees中缺少专门带初始间隙的SMA本构模型。通过图5和图4的串联实现,见图6。图中各参数含义为:E为弹性模量,取1.3×108kPa;δ为初始间隙;Fy为屈服应力,取3.89×107kPa;k1为材料初始刚度,取1.3×108kPa;k2为材料屈服刚度,取2.3×106kPa;β为正反向应力之比,取0.51。

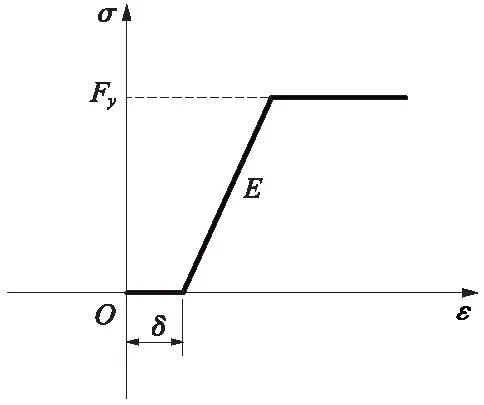
图5 uniaxialMaterial ElasticPPGap本构Fig.5 uniaxialMaterial ElasticPPGap constitutive

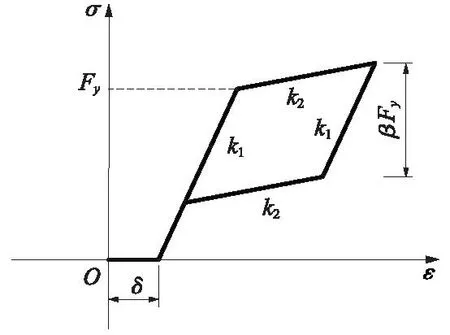
图6 串联后的SMA本构Fig.6 SMA constitutive after series

串联后SMA本构,取k1=6.5×107kPa,k2=2.3×106kPa,Fy=3.89×105kPa,β=0.51,与文献[21]中取值相同。

从美国太平洋地震研究中心(peer)选取3条地震波,分别为1940年El-Centro地震记录,1994年Northridge地震记录和1952年Taft地震记录,见表1。

表1 地震动输入信息Tab.1 Ground motion input information

5组初始间隙的墩顶水平位移与墩底弯矩地震反应列于表2,典型时程曲线如图7～图9所示。

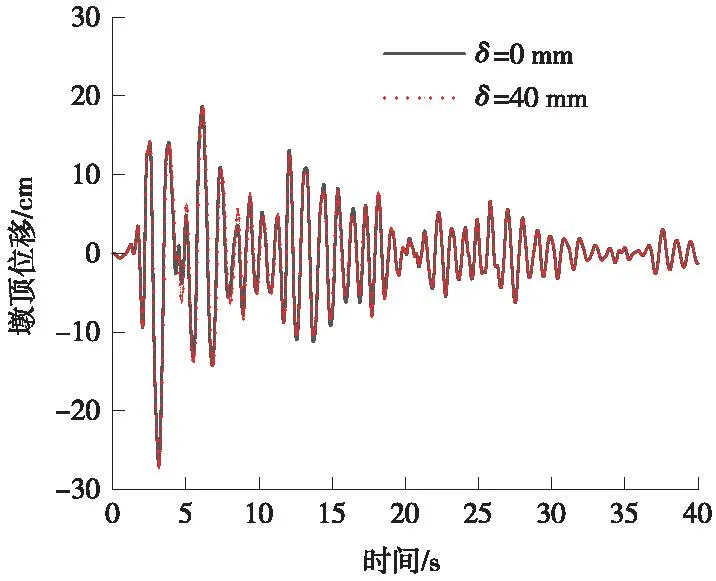
图7 墩顶水平位移时程曲线(El-Centro)Fig.7 Time-distance curve of horizontal displacement at the top of the pier (El-Centro)

El-Centro地震动作用下,初始间隙δ=40 mm时,由于初始间隙较大,SMA拉杆基本未起到限位作用,此时桥墩的地震反应接近没有限位的自由摇摆。由图7、图8可以看出,SMA限位中的曲线与自由摇摆的曲线形状吻合较好(这说明当前设计的限位装置基本没有改变自由摇摆桥墩的动力特性),再结合表2可知两者仅在最大值处略有差异。

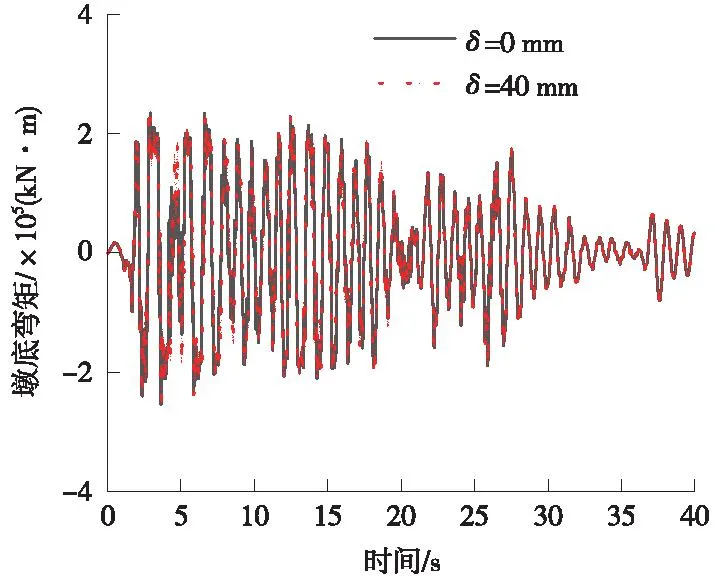
图8 墩底弯矩时程曲线(El-Centro)Fig.8 Time-distance curve of bending moment at the base of the pier (El-Centro)

由图9可以看出,El-Centro地震作用下,初始间隙δ=10 mm时,SMA限位拉杆已进入屈服耗能阶段,但耗能能力尚未充分发挥。

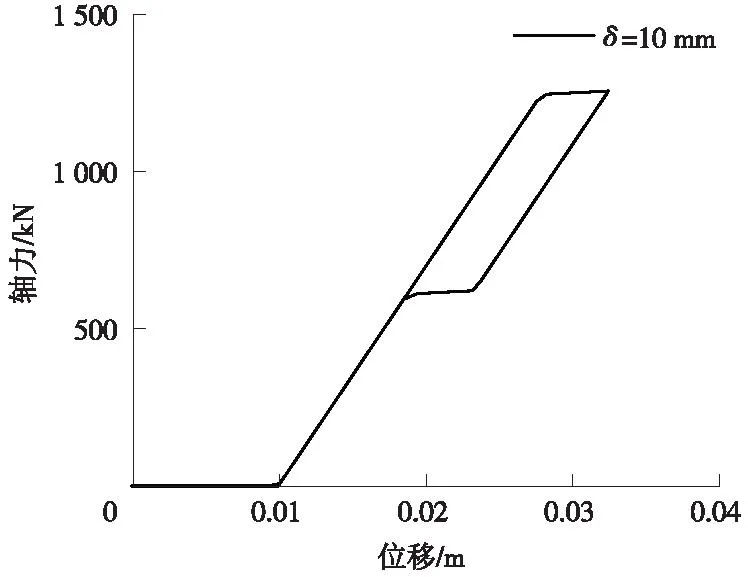
图9 SMA滞回曲线(El-Centro)Fig.9 SMA hysteresis curve (El-Centro)

由表2可知,不同初始间隙下3条地震波下的地震反应有一定离散性,其中Northridge波下的反应远大于EL-Centro波与Taft波,这是因为Northridge波是近断层地震动,而El-Centro波与Taft波是普通地震动。δ从30 mm 逐渐减小到0 mm,墩顶水平位移也随之减小,这是因为初始间隙大的SMA拉杆需要更大的应变才能屈服。δ=40 mm与δ=0 mm相比,El-Centro作用下墩顶水平位移减少1%;Taft波作用下,墩顶水平位移基本没变,这是因为初始间隙δ=40 mm时,SMA拉杆未起到限位作用,所以水平位移基本保持不变。Northridge波作用下,墩顶水平位移增大4%。

由表2还可知,δ从40 mm减小到0 mm,El-Centro作用下墩底弯矩增大3%;Taft波作用下,墩底弯矩增大1%;Northridge波作用下墩底弯矩减小3%。

4 初始预加力对地震反应的影响分析

18号墩底恒载的竖向力之和为37 599 kN。为探讨初始预加力的影响,取初始预加力分别为竖向力的0%,1%,2%,3%,4%。SMA杆面积布置及长度与前文相同,采用uniaxialMaterial InitStrainMaterial命令施加初应变来实现施加初始预加力,根据文献[20]初应变按下式计算

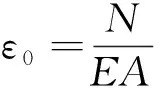
(1)

墩顶水平位移见图10,墩底弯矩见图11,SMA滞回曲线见图12。

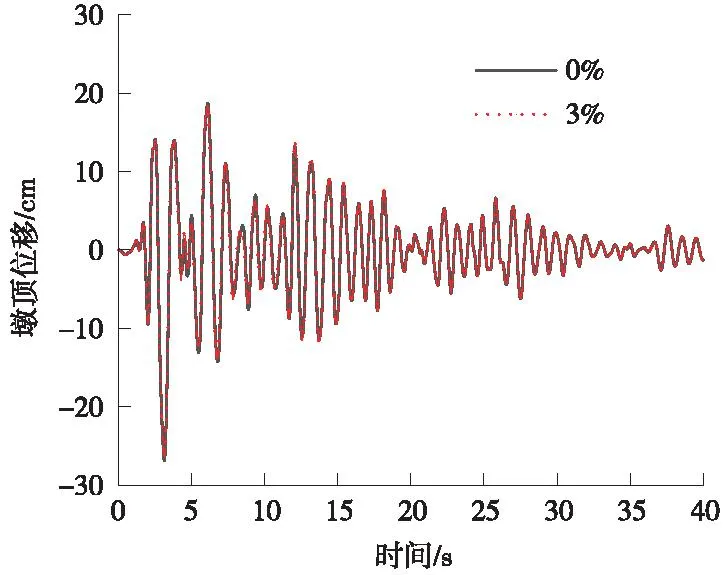
图10 墩顶水平位移时程曲线(El-Centro)Fig.10 Time-range curve of horizontal displacement at the top of the pier (El-Centro)

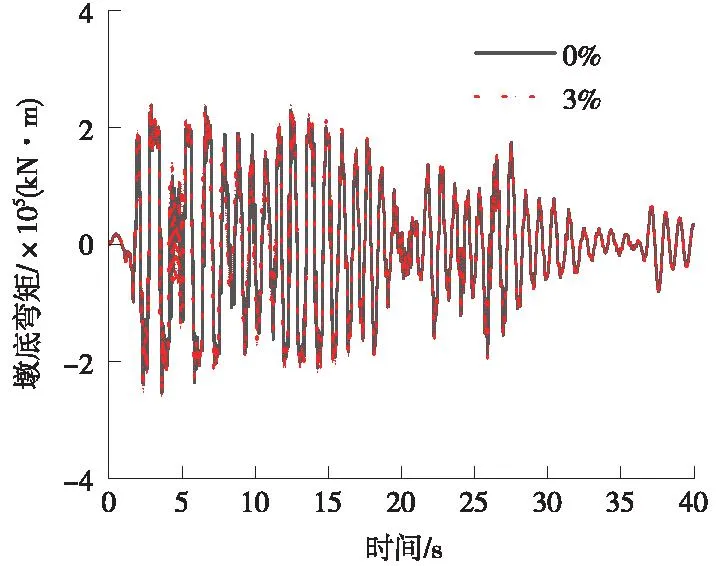
图11 墩底弯矩时程曲线(El-Centro)Fig.11 Time-dependent curve of bending moment at the base of the pier (El-Centro)

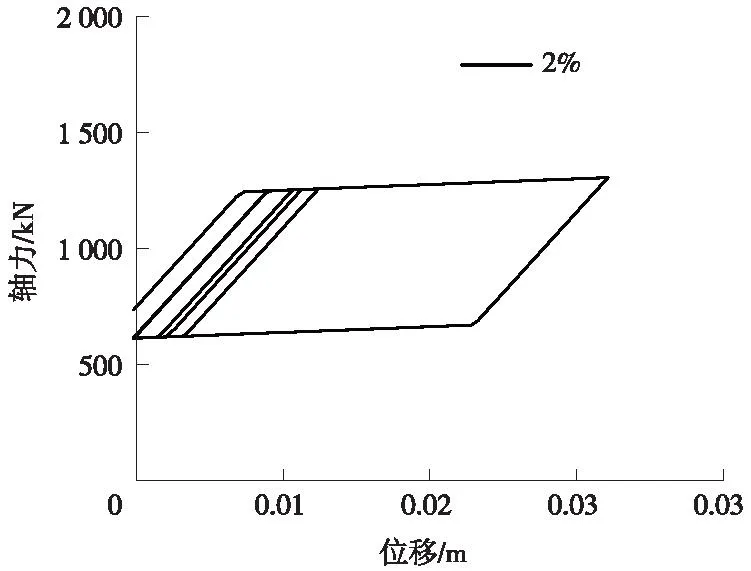
图12 SMA 滞回曲线(El-Centro)Fig.12 SMA hysteresis curve (El-Centro)

从图10可以看出,El-Centro波作用下,竖向力3%的初始预加力与无初始预加力的墩顶水平位移吻合较好,只有最大值有所减小。

从图11可以看出,El-Centro波作用下,在0～5 s时间段,竖向力3%初始预加力的墩底弯矩大于无初始预加力的墩底弯矩,其他时间段吻合较好。

SMA拉杆屈服应力为3.89×105kPa,对应SMA拉杆的屈服力为1245 kN,初始预加力为竖向力的4%,初始预加力大于屈服力,此时SMA拉杆已经屈服失效。由图12可以看出,预加力为竖向力2%,此时SMA拉杆已经屈服,发挥了耗能能力。

不同初始预加力地震反应比较见表3,可以看出,预加力减小了墩顶水平位移。随着初始预加力增大,El-Centro波作用下墩顶水平位移减小1%。Taft波作用下位移减小6%,Northridge波作用下位移减小1%。随着初始预加力增大,El-Centro波作用下墩底弯矩增大2%,Taft波作用下墩底弯矩增大4%,Northridge波作用下墩底弯矩增大3%。

表3 不同初始预加力地震反应比较Tab.3 Comparison of seismic responses with different initial prestress

5 SMA限位与预应力筋限位对比分析

为使SMA拉杆与预应力筋屈服,将选取的3条地震波的地震动幅值统一调整为0.57g,输入方向为顺桥向的水平方向。预应力筋刚度及面积与SMA拉杆相同,为A=0.003 2 m2,布置与前文SMA布置相同,无初始间隙和初始预加力,预应力钢筋采用文献[20]中的方法模拟,设置以下3种工况进行分析。工况1—自由摇摆、无限位装置;工况2—预应力钢筋限位的受控摇摆;工况3—SMA限位的受控摇摆。在El-Centro波下,桥墩的典型摇摆反应时程曲线如图13～图16所示。3种工况下墩顶水平位移、墩底弯矩以及竖向提离位移地震反应见表4。

表4 3种工况地震反应分析Tab.4 Seismic response analysis for 3 working conditions

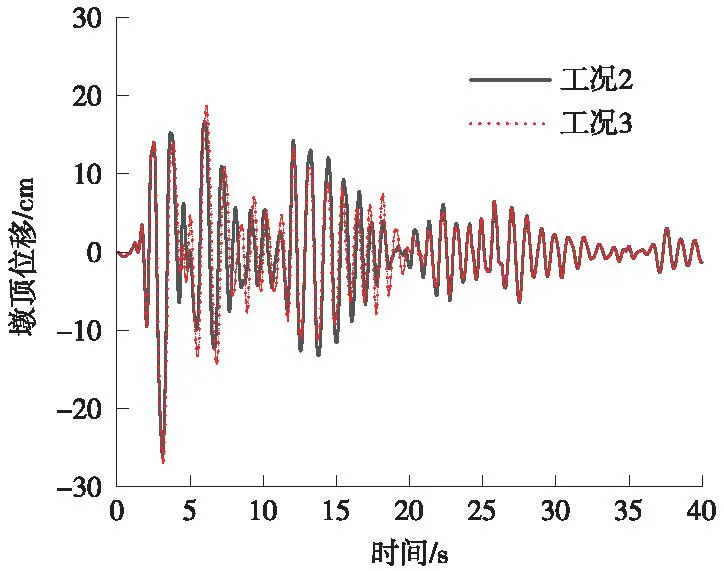
图13 墩顶水平位移时程曲线(El-Centro)Fig.13 Time-range curve of horizontal displacement at the top of the pier (El-Centro)

由图13可知,在0～5 s,墩顶水平位移最大,同时工况3墩顶位移大于工况2;在5～10 s时间段,工况3墩顶水平位移大于工况2,在10～20 s时间段,工况3墩顶位移小于工况2,限位装置起到限位的作用。其他时间段工况3和工况2吻合较好,这是因为预应力钢筋的弹性模量比SMA的弹性模量大,所以预应力筋限位的墩顶位移比SMA杆限位的小。

从图14可以看出,0～5 s和15～20 s时间段,工况3墩底弯矩小于工况2,SMA限位相对于预应力筋限位,减小了墩底弯矩。其他时间段,工况3和工况2曲线吻合较好。

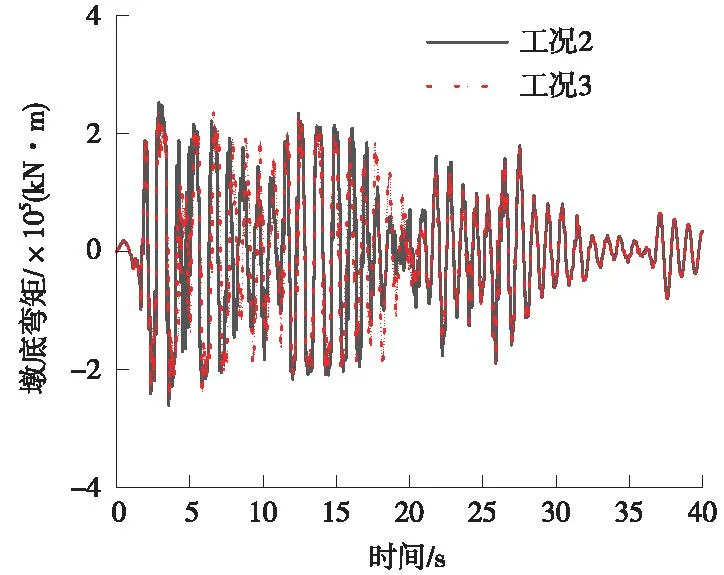
图14 墩底弯矩时程曲线(El-Centro)Fig.14 Time-distance curve of bending moment at the base of the pier (El-Centro)

结合图15及表4可知,SMA限位的受控摇摆与自由摇摆相比,SMA限位减少了桥墩的提离位移和提离次数;与预应力钢筋限位相比,提离位移限位稍差。

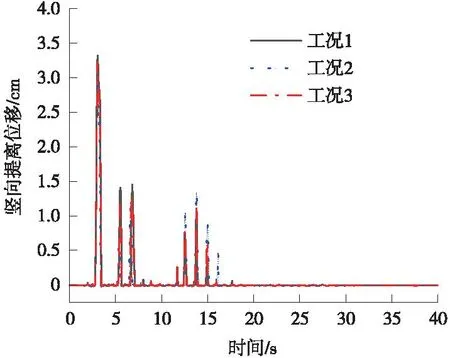
图15 桥墩基础的提离位移(El-Centro)Fig.15 Lift-off displacement of pier foundation (El-Centro)

由图16可知,El-centro波,工况3比工况2拉力小,这是因为SMA杆的屈服力小于预应力筋的屈服力。

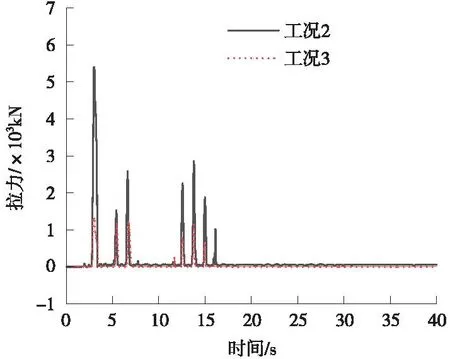
图16 限位装置拉力时程曲线(El-Centro)Fig.16 Restrainer device tension time curve (El-Centro)

表4可以看出,SMA限位比自由摇摆的自复位桥墩墩底弯矩大,这是因为SMA增大了桥墩的初始提离弯矩,而墩底弯矩与初始提离弯矩有关。SMA限位墩底弯矩比预应力筋限位的墩底弯矩小,这是因为SMA拉杆的耗能能力比预应力筋强。在El-centro波下,和自由摇摆相比,工况2的墩底弯矩增大6%,工况3增加3%。由图13和表4可知,墩顶水平位移工况2减小5%,工况3减小2%。

将计算结果与文献[5]和文献[20]进行对比,计算结果可靠。

6 结论

(1)提出了自复位桥墩中只受拉不受压的SMA限位装置模拟方法,且能考虑初始间隙与施加初始预加力。

(2)在普通地震动El-Centro与Taft作用下,随着限位装置初始间隙减小,SMA限位的自复位桥墩墩顶位移减小,墩底弯矩增大。在近断层地震动Northridge波下则不具有这一规律。

(3)随着限位装置初始预加力增大,SMA限位的自复位桥墩墩顶位移减小,墩底弯矩增大。

(4)SMA限位和自由摇摆相比可以减小桥墩顶部水平位移,减小提离位移和提离次数,但会增大墩底弯矩。与预应力钢筋限位相比,SMA限位的墩顶位移限位效果稍差,但不会显著增大墩底弯矩。