高铁隧道内地下水作用下双块式无砟轨道道床板裂缝扩展研究

刘成坤，陈进杰，黄守刚，王 瑞，陈 龙，李 杨

(1.石家庄铁道大学土木工程学院,石家庄 050043; 2.石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室,石家庄 050043; 3.河北省岩土工程安全与变形控制重点实验室,河北沧州 061001)

引言

双块式无砟轨道是我国高速铁路无砟轨道结构主要形式之一,因其施工方便、结构简单、整体性好等优点被广泛应用于武广、郑西、兰新等高速铁路[1]。然而,在新建成兰铁路某岩溶隧道内,双块式无砟轨道在施工期间出现水致伤损,整体性能不断劣化。现场调研发现,在岩溶地下水的侵蚀作用下,地下水易钙化形成结晶并挟裹泥沙造成隧道内排水系统的堵塞失效。而铁路隧道通常采用半包半排防排水设计[3],只在结构边墙、顶板或拱部设防水层及排水系统,底板或仰拱不设防排水系统。一旦排水系统堵塞,必然导致仰拱下地下水压的突增,严重时可能引起道床板底涌水、道床板隆起开裂(图1),影响无砟轨道的平顺性从而危及行车安全[5]。

图1 道床板底涌水、道床板横向贯通裂缝Fig.1 The water gushing at the bottom of the bed plate and the transverse through cracks of the bed plate

根据现场人员反映,在道床板施工完成后,发现道床板极易出现横向贯通裂缝。尽管双块式无砟轨道允许出现裂缝,且裂缝宽度未超出无砟轨道养护维修限值,但在水压的反复作用下,裂缝尖端会沿道床板横向不断扩展直至贯通。水压力作用下道床板开裂与岩石、土体的水力劈裂相似,国内外学者在无砟轨道水损坏方面开展了大量研究。断裂力学是无砟轨道裂纹的主要研究方法之一[6],在无砟轨道水致损伤的研究中,水通过裂纹渗透到混凝土中,在这种情况下遵循线性达西定律[8],但随着列车的趋近和远离,会在裂纹内产生周期性动水压力[9],这将加速裂纹的扩展,并在裂纹尖端形成掏空[10]。有限元计算结果表明,荷载幅值对无砟轨道裂纹内动水压力影响较大,随着列车荷载增加, 裂纹内控制点水压力呈线性关系增大[11],列车运行速度对无砟轨道层间裂纹的扩展也有较大影响,裂纹内动水压力随列车运行速度增加而增大[12]。沿着裂纹出口方向,水压力呈减小趋势[13],其最大值发生在裂纹尖端处;动水压力与列车速度近似呈二次方关系,与荷载幅值呈线性关系。在列车荷载和水的耦合作用下,无砟轨道层间裂纹尖端的应力强度因子(sif)增大,裂纹以剪切型破坏为主[14],裂纹长度是影响裂纹尖端应力强度因子的关键因素[15-16]。以上研究大多以动荷载作用下无砟轨道的水力伤损为主,而富水隧道内地下水压导致的道床板隆起开裂方面的研究尚存在大量空白。因此,明确水压作用下无砟轨道各结构层的力学响应,精准把控道床板伤损发展机制,确保轨道结构的耐久性,已然成为无砟轨道建设和运营中的重点研究内容之一。

1 隧道-无砟轨道模型

1.1 仿真模型建立

为研究隧道内CRTSⅠ型双块式无砟轨道道床板在水压作用下结构的受力变形特性,建立施工阶段隧道-无砟轨道结构计算模型。在初期支护周围施加法向的曲面接地弹簧,模拟围岩对隧道初期支护的约束作用,弹簧反力系数为150 MPa/m[17],模型纵向全长范围内均有水压作用。道床板、仰拱填充、仰拱长均为12m,为消除边界效应,模型选取3块道床板进行计算,以中间单元板作为研究对象,如图2所示。隧道内双块式无砟轨道结构参数[18-19],如表1所示。

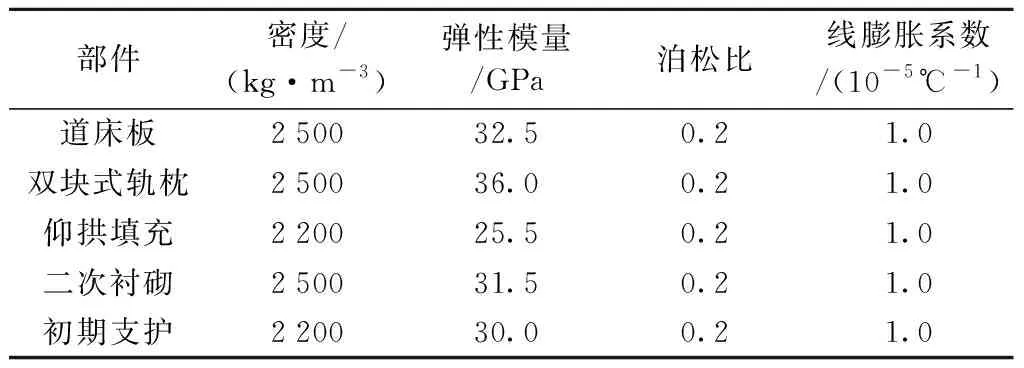
表1 隧道内双块式无砟轨道结构参数Tab.1 Structural parameters of double block ballastless track in tunnel

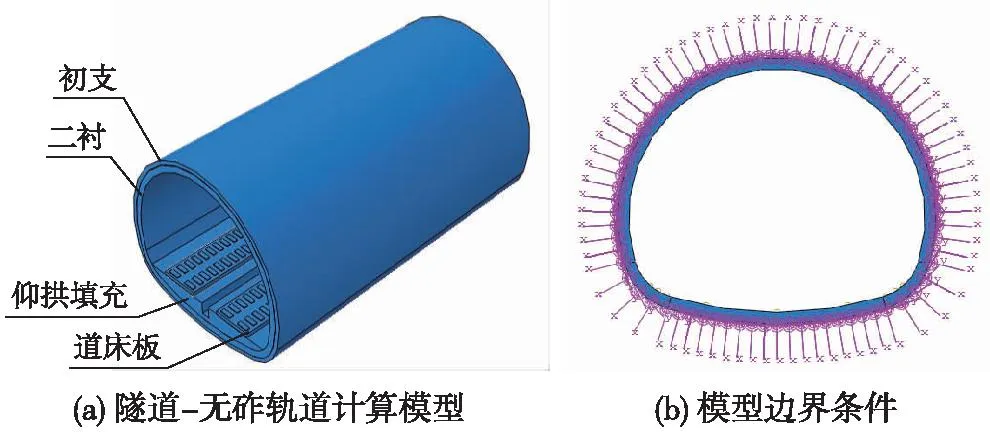
图2 隧道内无砟轨道结构模型Fig.2 Ballastless track structure model in tunnel

1.2 模型验证

为验证有限元模型的正确性,施加与文献[20]相同的荷载工况,有限元模型计算结果如图3所示。计算结果与文献仿真结果对比如表2所示。比较分析可知,本文计算的仰拱最大隆起位移与文献的仿真结果高度吻合。因此,本文建立的有限元模型可靠,可用于后续计算。

表2 数据对比分析Tab.2 Comparative analysis of data

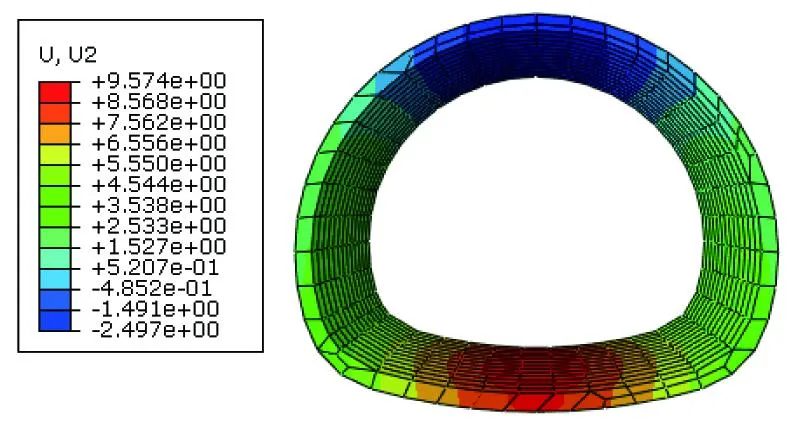
图3 衬砌变形云图(单位:mm)Fig.3 Cloud map of lining deformation (unit: mm)

2 仿真工况分析

针对隧道内排水管系统堵塞的情况,可认为在某区段内地下水无法通过排水管排出,从而造成仰拱底部形成较高的水压荷载使道床板隆起开裂。根据文献[21-22]的研究成果,并结合现场调研情况,可假定仰拱下沿线路纵向的水压力荷载分布形式为均匀分布、三角形分布。当隧道内排水系统完全堵塞时,可认为仰拱下水压沿线路纵向呈均匀分布;排水系统未堵塞时,可认为排水管位置水压接近为0,两排水管之间水压最高[23],相邻两排水管间距为6 m,沿线路纵向呈三角形分布,如图4所示。

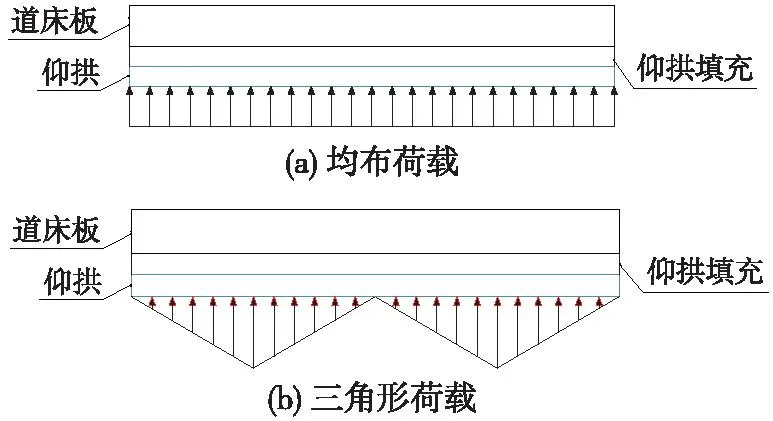
图4 水压力纵向分布示意Fig.4 Vertical distribution of water pressure

根据施工现场的测试结果,在隧道内排水系统堵塞较为严重区段实测水压约为0.5 MPa,故可假定仰拱下水头高度分别为30 m(0.3 MPa)、40 m(0.4 MPa)、50 m(0.5 MPa),并考虑混凝土温缩荷载的影响。根据我国TB 10003—2016《铁路隧道设计规范》[17]第5.3.2条规定,道床板混凝土收缩等效降温按10 ℃考虑,工况分析如表3所示。

表3 仿真工况分析Tab.3 Simulation condition analysis

3 仰拱隆起对轨道平顺性的影响

为研究仰拱隆起对轨道结构平顺性的影响,在温缩荷载为-10 ℃,水压荷载分别为0.5,0.4,0.3 MPa的条件下,仰拱、仰拱填充、道床板位移最大隆起量如表4所示。

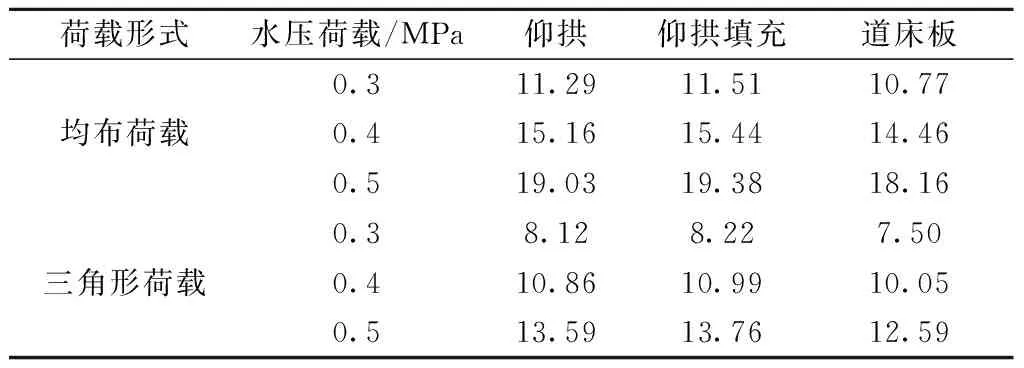
表4 无砟轨道各结构层最大隆起量 mmTab.4 Maximum uplift of each structural layer of ballastless track

由表4可以看出,在不同水压作用下无砟轨道各结构层的隆起量不尽相同,但总体上均随仰拱隆起量的增大而增大。在同一荷载形式下,随着水压增大,轨道结构各层的隆起量也不断增加。仰拱填充和道床板的隆起量不同,是由于文中将道床板与仰拱填充均考虑为弹性材料,且道床板弹性模量较大,所以道床板的隆起量相对于仰拱填充要小,并且导致仰拱填充与道床板间出现离缝。随着水压增加,离缝现象会更加明显,三角形荷载作用下,水压为0.5 MPa时,仰拱填充与道床板之间离缝为1.17 mm;均布荷载作用下,水压为0.5 MPa时,仰拱填充与道床板之间离缝则可达1.22 mm。在水压不变的情况下,无砟轨道各结构层隆起量差异不是很大,但随着水压增大,结构层间的离缝现象会更加明显,从而影响轨道结构的平顺性。

道床板位移隆起量随水压的变化曲线如图5所示。由图5(a)可知,均布荷载作用下随着水压增大,道床板位移隆起量不断增加,且位移隆起峰值位于道床板中部。当水压为0.3 MPa时,道床板位移隆起量最大可达10.76 mm,由于该条铁路设计时速为200 km,根据我国高速铁路静态几何尺寸允许偏差管理值[24],高速铁路在限速200 km/h时,高低允许偏差限值为8 mm,故水压在0.3 MPa以上时,道床板位移最大隆起量已超出高低允许偏差限值,这将影响轨道结构平顺性。由图5(b)可知,在三角形荷载作用下,道床板位移最大隆起量相较于图5(a)有所减小。当水压为0.4 MPa时,道床板位移最大隆起量为10.05 mm,故在水压0.4 MPa以上时,道床板最大隆起位移才会超出高低允许偏差限值,进而影响轨道结构平顺性。这表明排水系统堵塞失效,会进一步导致道床板隆起开裂,并加速道床板裂缝的扩展,影响行车的平稳与安全性。

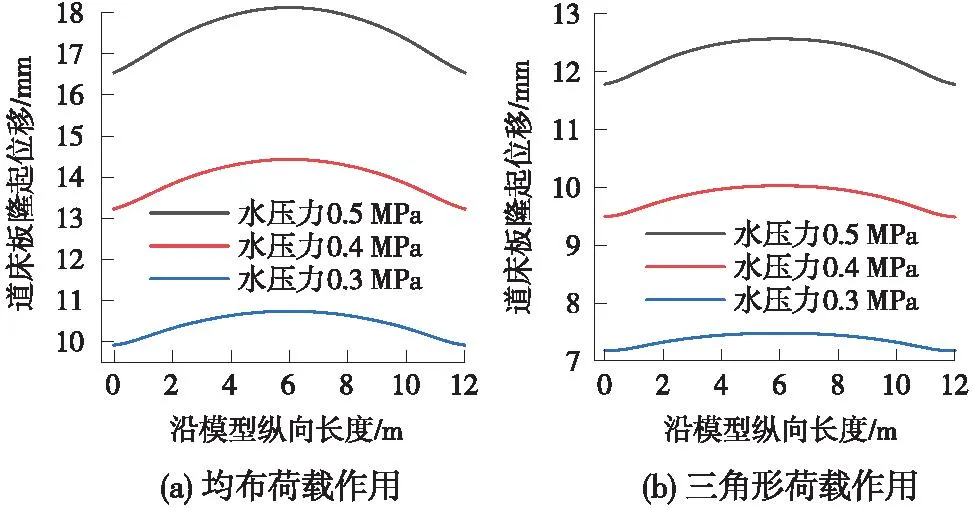
图5 不同水压下道床板位移隆起量Fig.5 Displacement and uplift of bed plate under different water pressure

4 双块式无砟轨道道床板裂纹扩展分析

基于有限元仿真计算结果,确定道床板结构受力的最不利位置,裂缝一般发展于此位置。结合FRANC3D软件,在道床板最不利位置插入不同形状的预制三维裂缝,研究水压、裂缝长度对道床板裂缝扩展的影响。

裂缝的失稳扩展可根据混凝土断裂力学中的断裂准则[25]:K≥KC,其中,K为裂缝的应力强度因子;KC为材料断裂韧度,是混凝土裂缝失稳扩展时的临界值(KC=54.7 N·mm-1.5)。通过计算相应工况下裂缝尖端应力强度因子,并与道床板混凝土断裂韧度临界值进行比较,从而判断裂缝是否失稳扩展,总结影响既有裂缝扩展的因素。

4.1 裂缝长度对裂缝扩展的影响

由于不同水压下道床板拉应力变化规律基本一致,故本次只选取最不利情况(仰拱下水压为0.5 MPa时),裂缝长度工况取为200,400,600,800,1 000 mm进行计算。计算结果共有Ⅰ型、Ⅱ型和Ⅲ型(张开型、滑开型和撕开型)3种类型的应力强度因子,并以a、b分别表示裂缝的两个尖端。

4.1.1 均布荷载下裂缝扩展分析

图6为均布荷载作用下,裂缝长度为对道床板裂纹扩展的影响。由图6可知,均布荷载作用下,裂缝尖端的Ⅰ型应力强度因子远大于Ⅱ型、Ⅲ型应力强度因子,道床板裂缝以张开型裂缝为主,故在判断裂缝扩展时只需考虑Ⅰ型应力强度因子的影响。从图6(a)可以看出,裂缝深度为60 mm时,随着裂缝长度增加,a、b尖端的应力强度因子逐渐增大。当裂缝长度为600 mm时,应力强度因子KIa=50.32 N·mm-1.5,KIb=48.27 N·mm-1.5,接近混凝土断裂韧度的临界值,这表明当裂缝长度大于600 mm时,裂缝尖端将沿道床板中部向两边发生横向失稳扩展。图6(b)展现了裂缝深度为80 mm时,应力强度因子随裂缝长度的变化趋势,当裂缝长度为200 mm时,a、b尖端的应力强度因子分别为KIa=53.24 N·mm-1.5,KIb=48.10 N·mm-1.5,接近混凝土断裂韧度的临界值,这表明当裂缝长度大于200 mm时,裂缝尖端将沿道床板中部向两边发生横向失稳扩展。

图6 均布荷载下裂缝长度对道床板裂缝扩展的影响Fig.6 Effect of crack length on crack propagation of pavement slab under uniform load

4.1.2 三角形荷载下裂缝扩展分析

图7为三角形荷载作用下,裂缝长度为对道床板裂纹扩展的影响。仍取KI进行分析,比较图6可知,同等条件下三角形荷载作用时裂缝尖端的应力强度因子小于均布荷载作用。由图7(a)可知,裂缝深度为60 mm时,随着裂缝长度增加,a、b尖端的应力强度因子逐渐增大。当裂缝长度为1 000 mm时,应力强度因子KIa=51.88 N·mm-1.5,KIb=51.37 N·mm-1.5,接近混凝土断裂韧度的临界值,这表明当裂缝长度大于1 000 mm时,裂缝尖端将沿道床板中部向两边发生横向失稳扩展。图7(b)代表了裂缝深度为80 mm时,裂缝尖端应力强度因子随裂缝长度增大不断增加。当裂缝长度为800 mm时,a、b尖端的应力强度因子分别为KIa=53.42 N·mm-1.5,KIb=54.48 N·mm-1.5,其值接近于混凝土断裂韧度的临界值,故认为当裂缝长度大于800 mm时,裂缝尖端将沿道床板中部向两边发生横向失稳扩展。

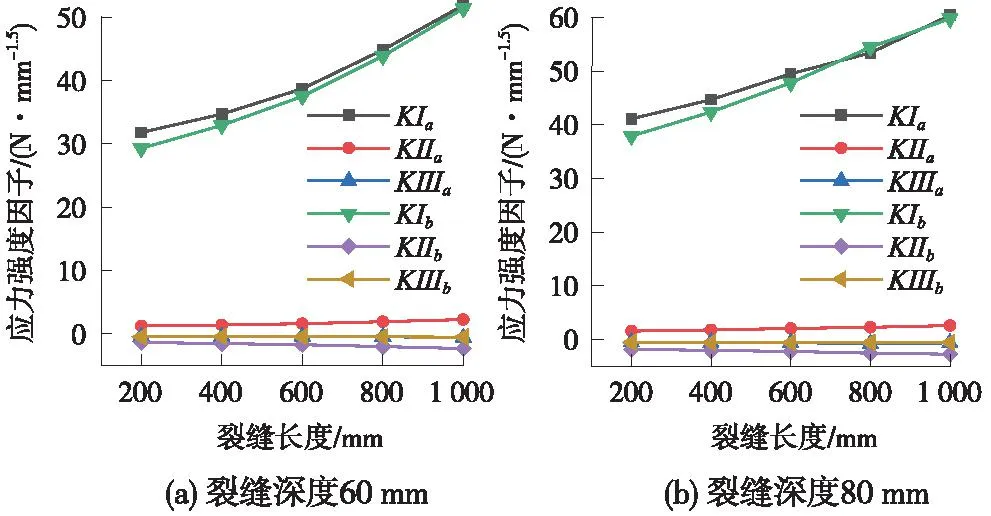
图7 三角形荷载下裂缝长度对道床板裂缝扩展的影响Fig.7 Effect of crack length on crack propagation of pavement slab under triangular load

从图6、图7可知,随着裂缝深度增加,裂缝的临界断裂长度逐渐减小,裂缝更容易发生失稳扩展。当裂缝的初始长度从200 mm增加至1 000 mm时,裂缝扩展速度增大,裂缝尖端应力强度因子很快到达裂缝失稳临界点。由此可见,裂缝的长度是裂缝失稳扩展的控制性因素,对裂缝的失稳扩展起关键性作用,均布荷载作用下若道床板产生裂缝,建议将裂缝长度控制在200 mm以内;三角形荷载作用下,若道床板产生裂缝,建议将裂缝长度控制在800 mm以内。

4.2 水压对裂缝扩展的影响

为研究不同水压下道床板裂缝尖端随裂缝长度的变化规律,选取最不利情况(裂缝深度80 mm)进行分析,由于道床板裂缝以张开型裂缝为主,故在判断裂缝扩展时仅考虑Ⅰ型应力强度因子的影响。

4.2.1 均布荷载下裂缝扩展分析

图8代表了裂缝深度为80 mm、不同水压条件下,裂缝长度对裂缝尖端应力强度因子的影响。由图8可发现,裂缝尖端的应力强度因子随水压增大而增大,当水压为0.3 MPa时,裂缝临界断裂长度接近800 mm,此时a、b尖端的应力强度因子为KIa=55.27 N·mm-1.5,KIb=57.14 N·mm-1.5,大于混凝土断裂韧度的临界值,道床板裂缝将沿尖端失稳扩展。当水压为0.4 MPa时,裂缝的临界断裂长度接近600 mm,此时a、b尖端的应力强度因子为KIa=56.85 N·mm-1.5,KIb=58.26 N·mm-1.5,大于混凝土断裂韧度的临界值,道床板裂缝将沿尖端失稳扩展。当水压为0.5 MPa时,裂缝的临界断裂长度约为200 mm,此时a、b尖端的应力强度因子为KIa=53.24 N·mm-1.5,KIb=48.10 N·mm-1.5,接近混凝土断裂韧度的临界值。由此可见,随着仰拱下水压增大,裂缝的临界断裂长度在逐渐减小,一旦裂缝长度大于其临界失稳长度,道床板中部区域裂缝将直接向两边发生失稳扩展。

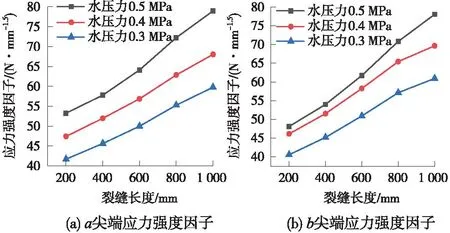
图8 均布荷载下水压对道床板裂缝扩展的影响Fig.8 Influence of water pressure on crack propagation of pavement slab under uniform load

4.2.2 三角形荷载下裂缝扩展分析

图9代表了裂缝深度为80 mm、不同水压条件下,裂缝长度对裂缝尖端应力强度因子的影响。对比图8可知,当沿线排水管未堵塞时,道床板裂缝尖端的应力强度因子有所减小,这表明排水管的泄压作用使得仰拱下水压减小,道床板结构受力得到了明显改善。由图9可发现,裂缝尖端的应力强度因子随水压增加而增大,当水压为0.3 MPa、裂缝长度达到1 000 mm时,此时a、b尖端的应力强度因子为KIa=48.47 N·mm-1.5,KIb=48.01 N·mm-1.5,小于混凝土断裂韧度的临界值。这表明当裂缝长度大于1 000 mm时,道床板裂缝尖端才会向两边发生失稳扩展。当水压为0.4 MPa时,裂缝的临界失稳长度约为1 000 mm,此时a、b尖端的应力强度因子为KIa=53.88 N·mm-1.5,KIb=54.42 N·mm-1.5,接近混凝土断裂韧度的临界值。当水压为0.5 MPa时,裂缝的临界失稳长度约为800 mm,此时a、b尖端的应力强度因子为KIa=53.42 N·mm-1.5,KIb=54.48 N·mm-1.5,接近混凝土断裂韧度的临界值。此时,道床板裂缝尖端不会向两边发生失稳扩展。

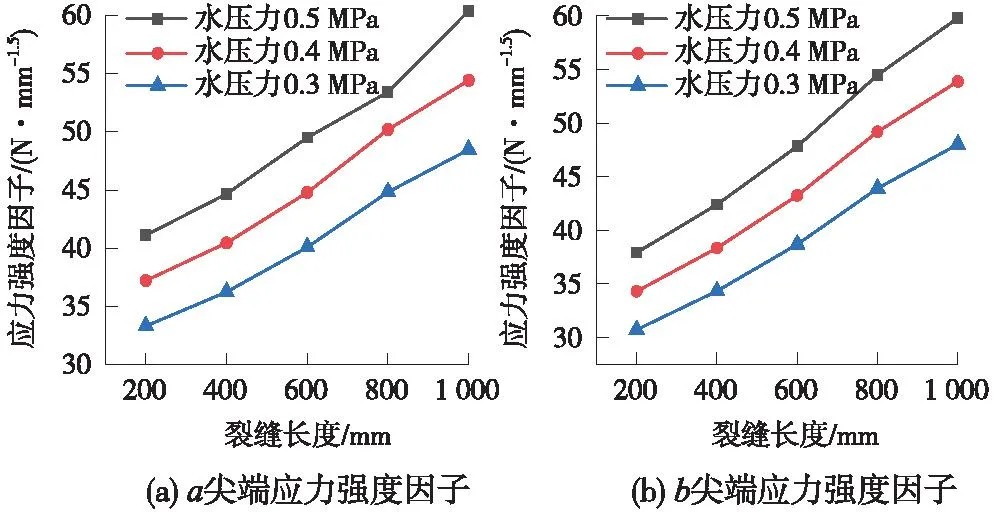
图9 三角形荷载下水压对道床板裂缝扩展的影响Fig.9 Influence of water pressure on crack propagation of pavement slab under triangular load

从图8、图9可知,随着水压增加,裂缝尖端的应力强度因子不断增大,裂缝更容易发生失稳扩展。此处不难发现,水压越大,道床板裂缝扩展越迅速。相同条件下,均布荷载作用时道床板裂缝尖端应力强度因子是对应三角形荷载作用时的1.2～1.4倍。综上所述,裂缝长度及水压大小是双块式无砟轨道道床板裂缝失稳扩展的关键影响因素,在仰拱下水压及道床板初始裂缝影响下,道床板极易隆起开裂,影响行车的平稳与安全性。

5 结论

以隧道内双块式无砟轨道为例,运用有限元软件,建立施工阶段双块式无砟轨道有限元模型,研究了水压作用下道床板的受力特性。并结合FRANC3D软件分析了水压、裂缝长度对道床板裂缝扩展的影响,主要结论如下。

(1)三角形荷载作用(排水系统未堵塞时)相较于均布荷载作用(排水系统完全堵塞时),道床板结构的位移隆起量均有所减小,但地下水压的反复作用始终会加速道床板裂缝的扩展,甚至会影响轨道结构的平顺性。

(2)裂缝长度是裂缝失稳扩展的控制因素。以均布荷载作用下排水管完全堵塞为最不利工况,在道床板养护维修时,应将裂缝长度控制在200 mm以内。

(3)同等条件下,水压越大,道床板裂缝扩展越迅速,均布荷载下道床板裂缝尖端应力强度因子是对应三角形荷载下的1.2～1.4倍。由此可见,排水系统堵塞失效会使道床板服役状态严重恶化。