基于3 m波长地铁钢轨焊缝接头不平顺的轮轨响应分析

徐 舟，从建力，赵铭洋，王 平，陈 嵘

(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031)

引言

钢轨接头是轨道结构中最薄弱的环节之一[1],接头会破坏轨道钢轨结构的连续性。地铁车辆通过接头时会产生频率高、幅值大的轮轨冲击力,一方面引起轨道结构的振动,对轨道结构造成损伤,另一方面也会产生噪音[2]和车体振动[3],影响乘客的乘坐体验,因此,对钢轨接头进行精确测量,研究钢轨接头不平顺激扰下的轮轨响应是十分必要的。

研究焊缝短波不平顺对轮轨系统的影响以及焊缝不平顺的发展演化规律对焊接头评估和管理有重要意义。杨云帆等[4]对实测钢轨焊接头1 m弦测数据进行统计分析,归纳焊接头不平顺波形主要包括谐波形、马鞍形、叠合形和多谐波形四种,并基于车辆-轨道垂向耦合动力学模型,提出了各类型接头不平顺的安全限值和打磨界限。高建敏等[5]则针对高速行车条件下焊缝不平顺的波长波深对轮轨系统的影响,提出了1 m直尺矢度条件下的高速铁路焊缝不平顺幅值安全限值。张克平[6]、翟婉明[7]、陈春俊等[8]基于车辆-轨道垂向耦合动力学模型,研究了钢轨焊缝接头的波长和波深对轮轨动力响应的影响,并通过改善轨道弹性减弱了轮轨响应。STEENBERGEN等[9]则通过研究焊缝几何形状和轮轨动态响应之间的关系,提出一个近似公式计算最大轮轨接触力。ZHANG等[10]根据实测1 m弦测值,在轮轨垂向耦合动力学模型的基础上考虑了轮轨接触模型和钢轨磨耗模型,探讨了车辆轴重、车速、焊缝硬度和长波不平顺对钢轨焊缝不平顺演化的影响。而牛留斌等[11]则基于有限元模型考虑车速和焊缝不平顺幅值的影响,分析发现,轮轨垂向力受焊接头不平顺幅值影响程度随车速增加而增大。陈嵘等[12]基于有限元方法建立了三维轮轨滚动接触模型,研究了钢轨焊接接头几何不平顺演变对轮轨接触行为的影响以及循环荷载作用下钢轨接头处的应力-应变响应。XU等[13]从实测出发,对重载线路的钢轨焊接接头跟踪测量,分析焊缝几何演化对轮轨相互作用的影响,描述了接头不平顺的几何演化过程。WEN[14]和LI等[15]将动力学模型和有限元模型结合,研究了轮轨作用力下钢轨焊缝接头处的材料变形特性。

但上述研究均采用焊缝不平顺的1 m弦测值,采用1 m长电子直尺测量,连续采样间隔5 mm,本文借助基于一弦N点弦测法制作的波磨仪16-18,连续采样间隔1 mm,可测波长范围2～3 000 mm,相较之下测得接头不平顺更接近真实的焊接头形态。将实测3 m波长焊缝接头不平顺数据激励输入车辆-轨道垂向耦合模型中,与传统1 m弦测值激扰下的轮轨动态响应进行对比,并分析车速和焊缝位置对轮轨响应的影响。

1 车辆-轨道垂向耦合动力学模型

车辆-轨道垂向耦合模型包含车辆模型和轨道模型(图1),二者依靠轮轨相互作用关系耦合,输入外部激励后,通过数值积分方法对系统进行求解。

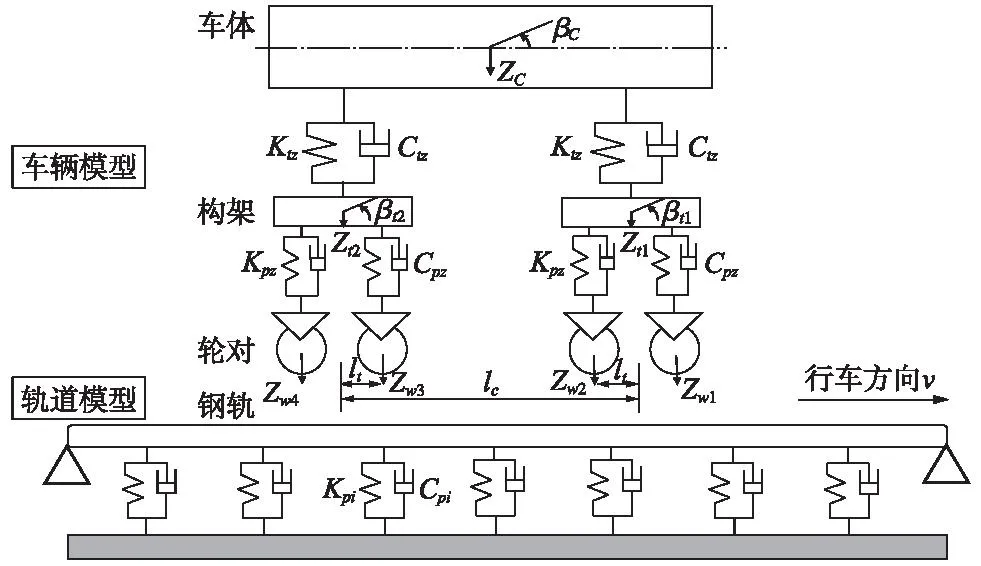
图1 车辆-轨道垂向耦合动力学模型Fig.1 Vehicle-track vertical coupling dynamics model

车辆系统视为一个多刚体系统,具有10个自由度,包括车体、构架的点头和沉浮运动以及4个车轮的沉浮运动,车辆模型的动力学方程可以参照文献[19]。

轨道模型考虑为整体道床式轨道,不考虑轨枕道床的自由度,钢轨视为连续弹性离散点支撑的Euler梁,截取轨枕支承点数一半的钢轨模态,钢轨的振动方程为

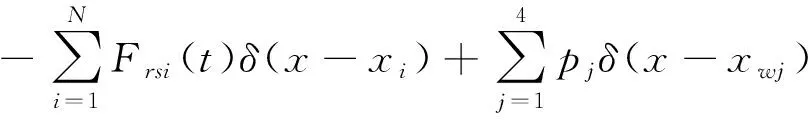
(1)

式中,EIY为钢轨抗弯刚度;mr为钢轨的单位长度质量;xwj(j=1～4)为车轮的运动坐标;pj(j=1～4)为轮轨相互作用力。

Frsi(t)=Kpi[Zr(xi,t)-Zsi(t)]+

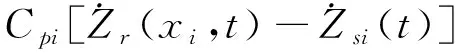
(2)

式中,Kpi和Cpi分别为轨下垫层的刚度和阻尼;Zsi(t)为轨枕振动位移,取为零。

引入钢轨的正则形坐标,整理得到Euler梁模型的钢轨振动微分方程如下

(3)

式中,qk(t)为钢轨正则形坐标;Zk(x)为钢轨的垂向振型函数。

基于Hertz非线性弹性接触理论,通过对轮轨垂向接触力的模拟仿真,确定轮轨之间的垂向作用力。

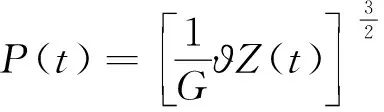
(4)

式中,G为轮轨接触常数;ϑZ(t)为轮轨之间的弹性压缩量。

G取磨耗形踏面车轮常数

G=3.86×R-0.115×10-8

(5)

在轮轨接触面上存在不平顺时,ϑZ(t)取

ϑZ(t)=Zwj(t)-Zr(xwj,t)-Z0(t)

(6)

此时,轮轨力表达式为

(7)

式中,j取值范围1～4;Zwj(t)为t时刻第j位车轮的位移;Zr(xwj,t)为t时刻第j位车轮下的钢轨位移;Z0(t)为界面不平顺。

整个车辆-轨道耦合系统的动力学方程可表示如下

[M]{A}+[C]{V}+[K]{X}={F}

(8)

式中,[M]为系统质量矩阵;[C]为系统阻尼矩阵;[K]为系统刚度矩阵;{A}为系统广义加速度矢量;{V}为系统广义速度矢量;{X}为广义位移矢量;{F}为系统广义荷载矢量。

选用快速显式积分法 (翟方法)[19]求解上述动力学方程,用前两步的位移、速度、加速度预测下一步位移量,并根据系统运动方程求解下一步加速度量。积分公式如下

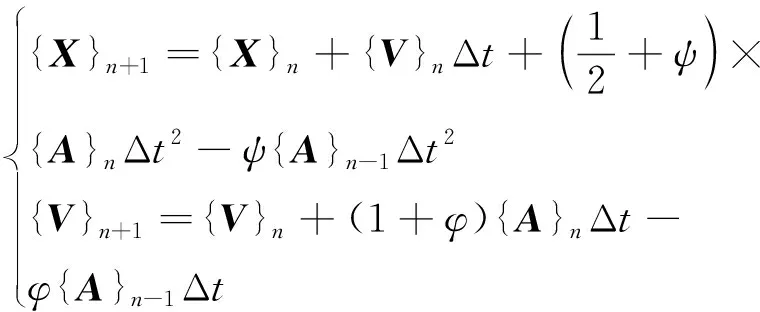
(9)

2 钢轨焊接接头实测与分析

为深入分析钢轨接头状态,需要对钢轨接头进行精确测量,本文利用基于一弦N点弦测法研制的波磨仪对地铁线路的钢轨接头进行了测量,图2为现场钢轨接头不平顺测量示意,图3为钢轨接头测量结果,图3中的青色曲线为样本接头不平顺,红色曲线为样本不平顺平均值。

图2 钢轨焊接接头不平顺现场测量Fig.2 Field measurement of irregularity of welded rail joints

测量接头共计720个,被测量接头中包含钢轨有缝接头和焊接接头。钢轨有缝接头在轮轨长期冲击荷载作用下,存在明显错台,如3(a)所示,占测量接头总数的5.18%;钢轨焊接接头可以分为“M”形和“W”形,“M”形焊接头形态如3(b)所示,接头不平顺波形呈“M”形,平均中心波深0.19 mm,平均中心波长1.93 m,在焊缝中心有一段低于轨面的下凹区域,焊缝中心两侧有对称的高于轨面的凸起,“M”形焊接头数量占测量接头总数的18.63%;“W”形焊接头如图3(c)～图3(f)所示,接头不平顺波形呈“W”形,平均中心波深0.33 mm,平均中心波长2.01 m,焊接头中心有一段高于轨面的凸起,焊缝中心两侧有对称的低于轨面的下凹,4种“W”形焊接头数量占测量接头总数的76.19%。

从波长和波深的角度分析,“W”形焊接头的中心波长和“M”形焊接头接近,但“W”形焊接头的平均中心波深大于“M”形焊接头。“M”形焊接头和W-1形焊接头的中心波深较小,幅值接近0.18 mm;W-2和W-3形焊接头的中心波深较大,幅值约0.32 mm;W-4形焊接头的中心波深最大为0.48 mm。分析焊接接头不平顺波形的对称性发现,M形焊接头、W-1形焊接头和W-4形焊接头,具有良好的对称性,W-2形焊接头偏向于右对称方向,W-3形焊接头偏向于左对称方向。

基于弦测理论模拟1 m弦测过程,对实测的3 m波长焊缝接头不平顺数据重新采样结果如图4所示。3 m波长焊缝不平顺幅值比重新采样得到的1 m弦测值幅值稍小,“M”形接头重新采样后接头不平顺幅值增大7.7%;4种“W”形焊接接头重采样后不平顺幅值分别增大11.9%、3.2%、3.4%、4%。

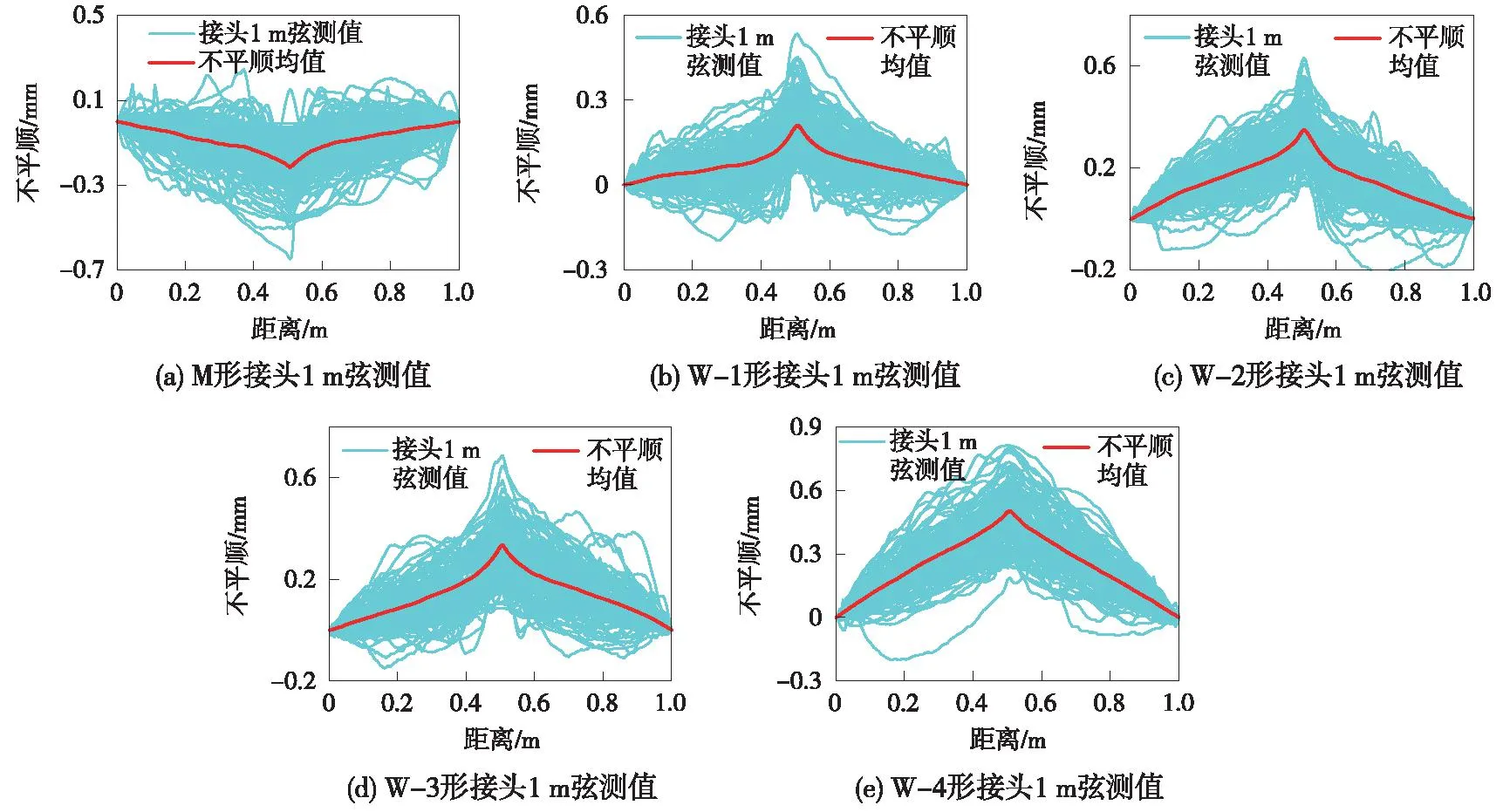
图4 焊接头1 m弦测值Fig.4 1m chord measurement of rail join

3 实测焊缝接头不平顺激扰下轮轨系统动态响应分析

为对比3 m波长焊缝接头不平顺和传统1 m弦测值对轮轨系统动态响应的影响,分别将3 m波长焊缝接头不平顺和1 m弦测值作为车辆-轨道垂向耦合模型的激励,对模型进行求解。每种类型接头选取60个样本,车速为40 km/h,考虑单个样本具有特殊性,所以计算每个样本下的轮轨响应后取平均值进行分析。

列车经过“M”形接头时,两种激励下轮轨系统响应如图5所示。1 m弦测值下的轮轨力和轮重减载率幅值分别为92.41 kN和0.07,轮对振动加速度和钢轨振动加速度分别为0.70g和6.69g;3 m波长下的轮轨力和轮重减载率幅值分别为92.76 kN和0.08,轮对振动加速度和钢轨振动加速度幅值分别为0.76g和6.81g。相比1 m弦测值的轮轨响应,3 m波长焊缝不平顺下的轮轨力变化很小,轮重减载率增大14.3%,轮对振动加速度增大8.6%,钢轨振动加速度增大1.8%。

图5 M形焊缝对应的轮轨动态响应Fig.5 Dynamic wheel-rail responses corresponding to M-shaped welds

图6～图9为列车经过4种“W”形接头的轮轨动态响应。由图6中列车经过W-1形接头时的轮轨响应可知,1 m弦测值的轮轨力和轮重减载率幅值分别为90.37 kN和0.12,轮对振动加速度和钢轨振动加速度幅值分别为0.79g和7.75g;3 m波长焊缝不平顺的轮轨力和轮重减载率幅值分别为90.39 kN和0.13,轮对振动加速度和钢轨振动加速度幅值分别为0.94g和9.08g。与1 m弦测值的轮轨响应相比,3 m波长焊缝不平顺的轮轨力幅值差异小,轮重减载率幅值增大8.3%,轮对振动加速度幅值增大19.3%,钢轨振动加速度幅值增大17.2%。

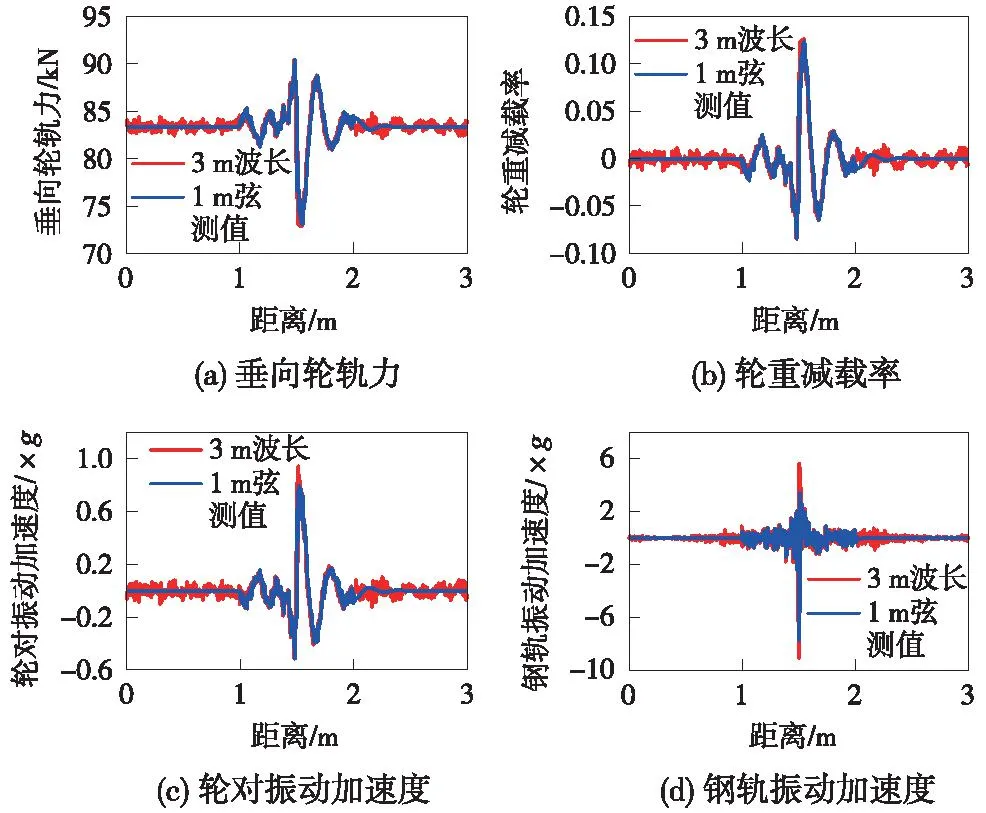
图6 W-1形焊缝对应的轮轨动态响应Fig.6 Dynamic wheel-rail responses corresponding to W1-shaped welds

从图7～图9可知,两种激励下,列车通过W-2、W-3和W-4形的焊缝中心处轮轨力幅值差异不明显,主要差异表现在轮重减载率和轮轨系统振动加速度上:对比通过W-2形接头时两种激励下的轮轨响应,3 m波长焊缝不平顺的轮重减载率幅值增大10.6%,轮对振动加速度幅值增大40.4%,钢轨振动加速度幅值增大75.7%;通过W-3形接头时,相比1 m弦测值的轮轨响应,3 m波长焊缝不平顺的轮重减载率幅值增大20.9%,轮对振动加速度幅值增大44.3%,钢轨振动加速度幅值增大72.8%;通过W-4形接头时,两种激励下的轮轨响应差异最明显,相比于1 m弦测值的轮轨响应,3 m波长焊缝不平顺的轮重减载率幅值增大25.3%,轮对振动加速度幅值增大80.96%,钢轨振动加速度幅值增大129.9%。

图7 W-2形焊缝对应的轮轨动态响应Fig.7 Dynamic wheel-rail responses corresponding to W2-shaped welds

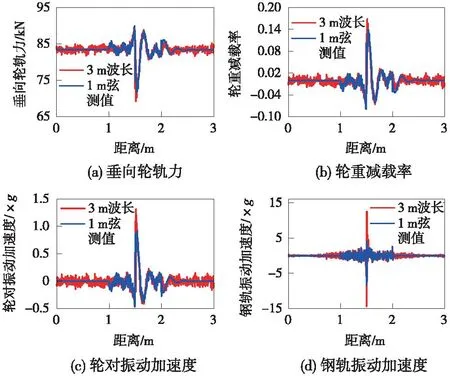
图8 W-3形焊缝对应的轮轨动态响应Fig.8 Dynamic wheel-rail responses corresponding to W3-shaped welds

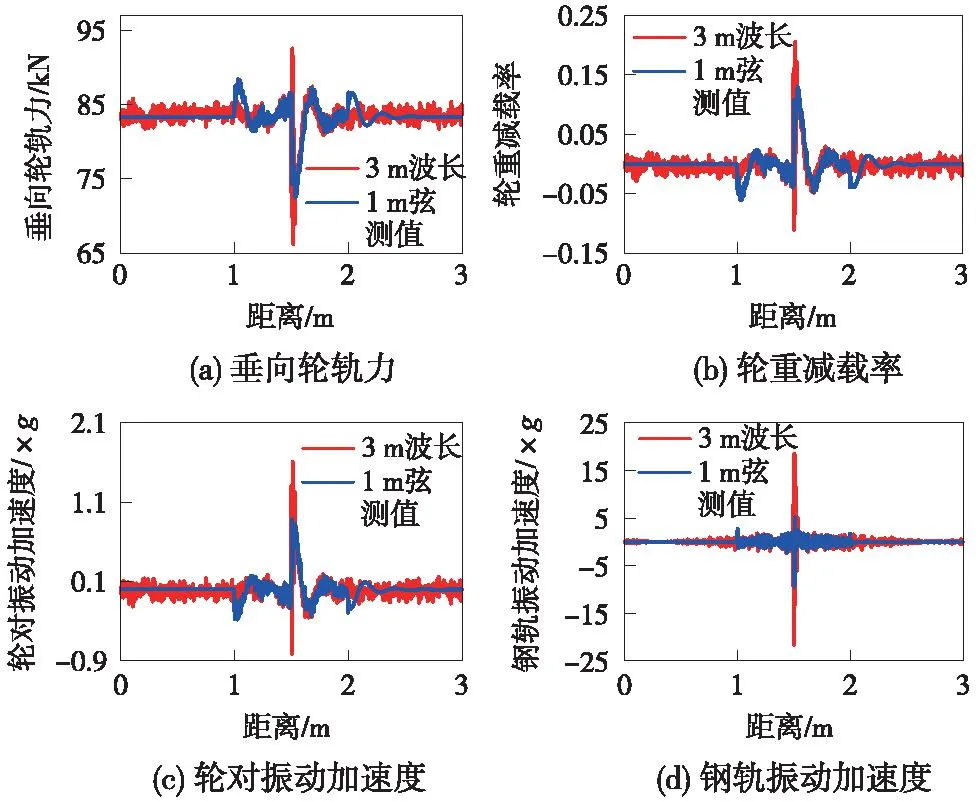
图9 W-4形焊缝对应的轮轨动态响应Fig.9 Dynamic wheel-rail responses corresponding to W4-shaped welds

将各个类型接头响应的对比结果加权计算之后,发现相对1 m弦测值的轮轨动力响应结果,3 m波长焊缝不平顺的轮轨力幅值变化不明显,轮重减载率幅值增大15.57%,钢轨加速度幅值增加54.05%,轮对振动加速度幅值增加37.67%。

图10(a)～图10(e)每列分别为“M”形和4种“W”形焊接接头的3 m波长焊缝不平顺和1 m弦测值激励下,轮轨力和钢轨振动加速度的功率谱密度。图中的功率谱密度曲线存在两个明显的频率范围,一个在中频段反映了轮轨共同弹性变形的耦合振动,另一个在高频段反映了由焊缝短波不平顺引起的高频振动。从图10(a)可知,列车通过“M”形接头时,两种激励下的轮轨力和钢轨振动加速度响应的两个频带基本一致,中频范围在40～85 Hz,高频范围在670～850 Hz,但相比3 m波长,1 m弦测值激扰下的响应功率谱密度的值略小。列车通过“W”形接头时,从图10(b)～图10(e)中可以发现,两种激励下的轮轨力和钢轨振动加速度响应的振动频率范围基本一致,中频振动范围在30～60 Hz,高频振动范围在650～880 Hz,同样相比3 m波长,1 m弦测值激扰下的响应功率谱密度的值略小。

<1)，且各件产品是否为不合格品相互独立．

图10 各接头轮轨力和钢轨加速度的功率谱密度Fig.10 Power spectral density of wheel-rail force and rail acceleration of each rail joint

4 车速和焊缝位置对轮轨力的影响

4.1 车速对轮轨力的影响

本节研究了列车分别以40,80,100,160,200 km/h速度通过3 m波长焊缝接头时的轮轨力响应,每类接头取60个样本计算轮轨力取平均值,在保证其他条件不变的情况下分析车速对轮轨力的影响。图11分别为列车经过M形接头、W-1形接头、W-2形接头、W-3形接头、W-4形接头的轮轨力响应和轮重减载率变化。

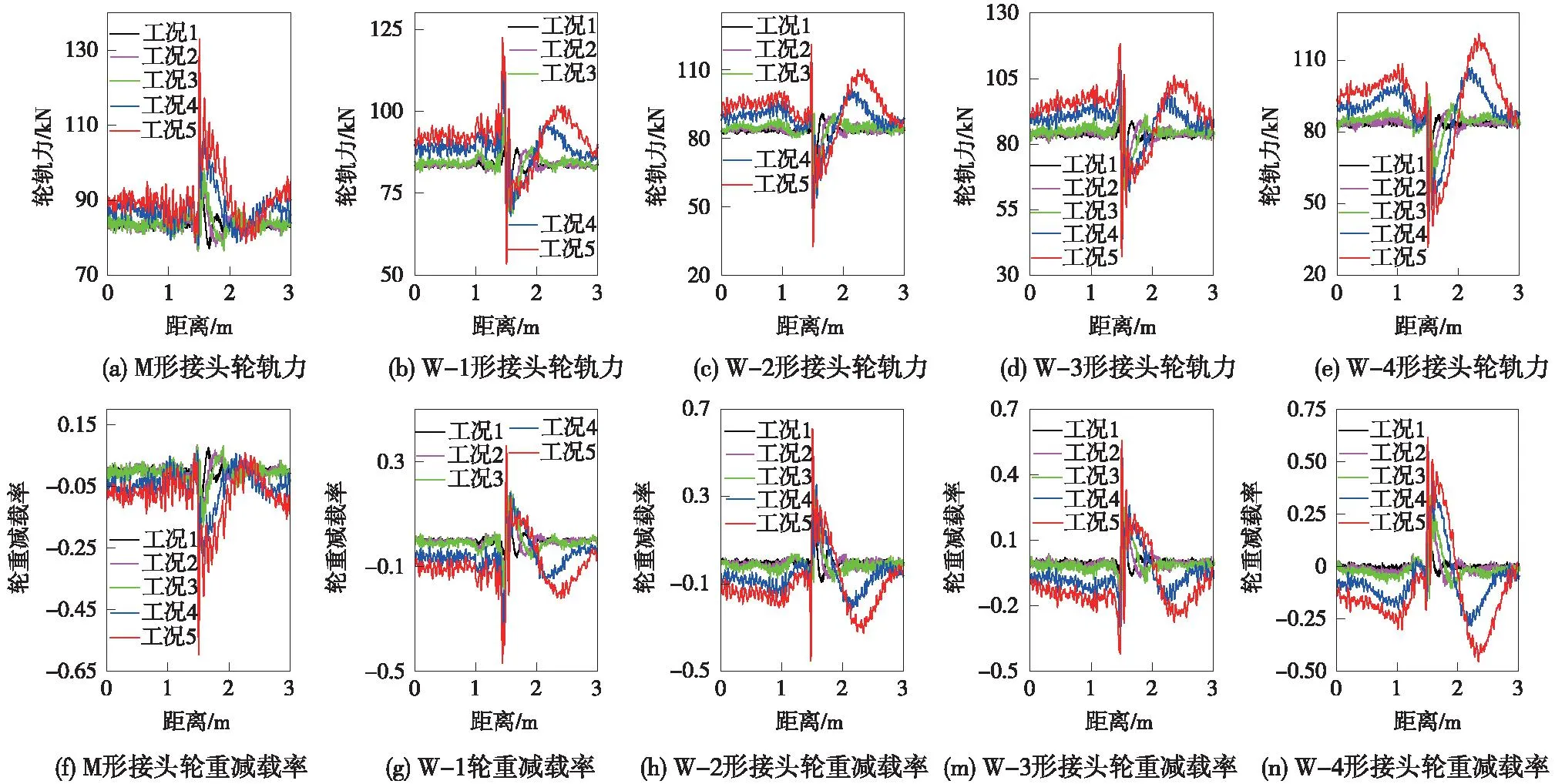
图11 不同车速下轮轨力和轮重减载率变化Fig.11 Changes of wheel-rail force and wheel load reduction rate at different speed

从图11(a)～图11(e)可知,随着车速提升,轮轨力波动更明显,轮轨力响应幅值增大,幅值变化情况见表1,同时从图中可以发现,列车经过接头中心1 m范围后的轮轨力还会增大。从图11(f)～图11(n)可知,列车提速同样会导致轮重减载率幅值变大。

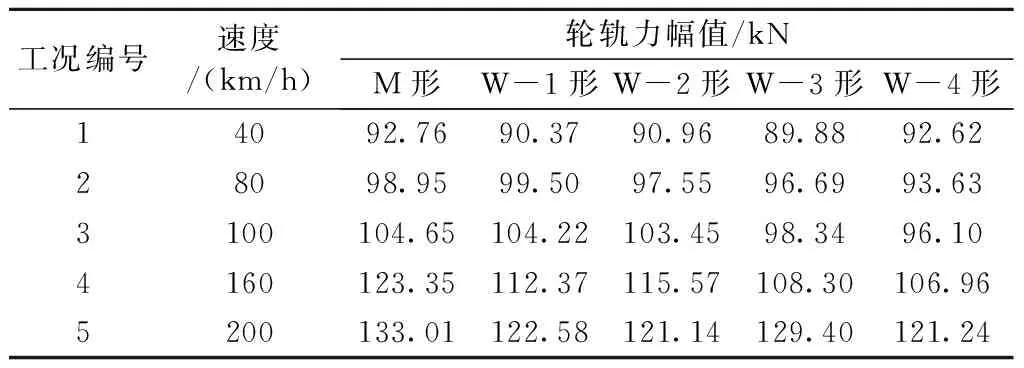
表1 各车速下的轮轨力幅值Tab.1 Amplitude of wheel-rail force at each speed

4.2 焊缝位置对轮轨力的影响

文献[20]指出,当焊缝在轨枕间不同位置处时,列车经过焊接接头的轮轨力会存在差异。将3 m波长焊缝不平顺分别施加在距离第170根轨枕0,0.1,0.2,0.3,0.4,0.5 m处,计算列车经过焊缝接头时的轮轨力变化情况。

图12(a)～图12(e)为各个工况下,列车以80 km/h速度通过每种接头时的轮轨力响应曲线,可以明显看出,随着焊缝中心里程后移,轮轨力的幅值及其出现的位置也会改变。各工况下列车通过接头时的轮轨力幅值如表2和图12(f)所示,随着焊缝中心位置改变,“M”形接头和“W”形接头的轮轨力幅值变化情况相反,当“W”形接头焊缝中心距轨枕越近,轮轨力幅值越大,当“M”形接头焊缝中心距轨枕越远时,轮轨力幅值越大;在焊缝中心位置保持不变时,工况1～工况5中W-4形的轮轨力幅值最大,工况6中“M”形接头轮轨力幅值最大。

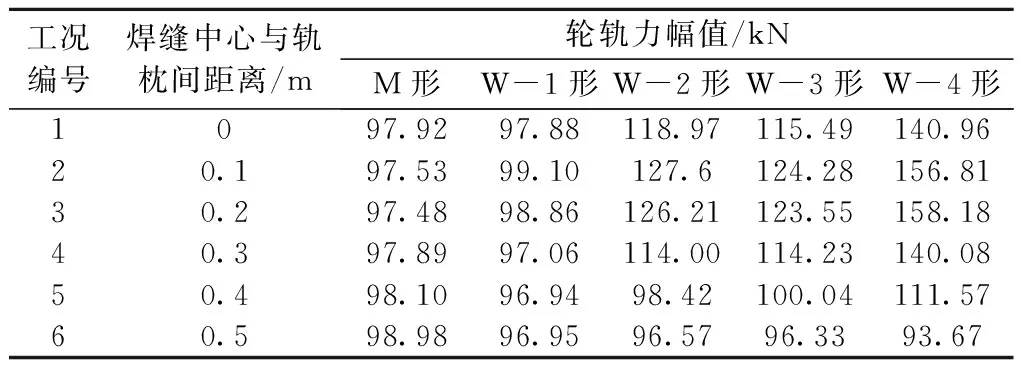
表2 焊缝在不同位置时轮轨力幅值Tab.2 Wheel-rail force amplitude of rail joint at different positions

图12 焊缝在轨枕间不同位置处的轮轨力Fig.12 Wheel-rail forces of the weld at different positions between sleepers

综合考虑列车双向行驶,当焊缝中心距轨枕0.1 m时,轮轨力的幅值最大。因此,在轨道铺设过程中应该考虑焊接中心的位置,同时后期在对接头养护维修时需要考虑不同位置处的接头损伤程度不一样,提高对距离轨枕两端较近接头的养护维修频率。

5 结论

本文借助基于一弦N点弦测法研制的波磨仪对线路接头进行测量,可获取2～3 000 mm波长范围的接头短波不平顺,结合车辆-轨道垂向耦合模型,对比3 m波长焊接头不平顺和1 m弦测值激扰下的轮轨响应,并考虑车速和焊缝中心位置对轮轨力的影响,分析结果得到如下结论。

(1)在地铁线路现场实测了6种接头,共计682个焊接头,其中“M”形焊接头134个,4种“W”形焊接头548个。

(2)3 m波长焊缝接头不平顺激扰下的轮轨响应相比1 m弦测值更大。3 m波长焊缝接头不平顺激扰下的轮轨力幅值变化不明显,轮重减载率幅值增大11.52%,钢轨加速度幅值增大54.05%,轮对振动加速度幅值增大37.67%;在频域上,两种激励下轮轨力和钢轨振动加速度的主频分布一致,但3 m波长焊缝接头不平顺激扰下的轮轨力和钢轨振动加速度功率谱密度值更大。

(3)列车在经过3 m波长焊缝中心后,轮轨力先减小后增大,车速提高会导致轮轨力变化幅度更明显,同时轮轨力幅值和轮重减载率幅值增大。

(4)随着焊缝中心与轨枕间距离增加,轮轨力幅值先增加后减小,当焊缝中心距轨枕0.1 m时,轮轨力幅值最大。

后续将开展5种焊缝接头的轮轨响应现场试验,研究3 m波长焊缝不平顺特征与轮轨响应的映射关系,为3 m波长焊缝的特征(幅值,波长)限值管理与服役状态评估提供数据支撑。