GNSS/INS 组合导航中自适应抗差KF 算法研究*

吴 昕 ，刘 超

（安徽理工大学空间信息与测绘工程学院，安徽 淮南 232001）

0 引言

全球导航卫星系统（Global Navigation Satellite System, GNSS）能够提供全天候的导航、定位以及授时服务，且定位误差不随时间累积[1]。但在复杂城市环境下，由于高大密集建筑物、茂密树木和高架桥等的遮挡，卫星信号频繁受到干扰，此时的观测值会受到影响，用户的定位精度也会受到影响[2]。惯性导航系统（Inertial Navigation System, INS）是一种完全自主的且被广泛使用的导航定位技术，但随时间增长其误差会快速积累，导致精度快速下降，因此无法满足长时间、高精度的导航定位需求[3-4]。因此，将GNSS和INS 结合起来可较好地满足用户的需求[5]。近年来，将两者融合以弥补单一系统的技术缺陷成为研究热点之一[6-7]。

在组合导航领域最常用的一种最优数据融合方法便是卡尔曼滤波（Kalman Filter, KF），其已经被广泛应用于数据处理领域。而标准卡尔曼滤波的状态参数想要得到最优估计，就需要准确获取状态模型参数、状态噪声协方差矩阵以及观测噪声的统计特性等信息[8]。然而，在实际应用中，状态模型参数及噪声统计特性是难以准确确定的，在很多情况下以上两类参数的获取都会存在一些误差，致使卡尔曼滤波的精度降低，严重时还可能会引起滤波发散，进而不能正确地反映载体运动状态[9-10]。

众多学者针对随机系统的系统噪声协方差矩阵Q和测量噪声协方差矩阵R进行在线估计，或者采用自适应抗差卡尔曼滤波（Adaptive and Robust Kalman Filter, ARKF）对其进行参数优化[11-12]。目前常用的构建自适应因子统计量的方法有状态不符值、速度不符值、方差分量比和量测新息。前三个构建方法要求在该时刻有多余观测信息，即该时刻的观测数据个数要多于待估状态参数的个数，否则在求解状态最优估计值时，使用最小二乘原理的方法会出现秩亏现象，所以这两个构建方法不适用于GNSS/INS 松组合[13]。在提出的改进的卡尔曼滤波算法中，使用量测新息构建马氏距离作为检验统计量，以判定观测数据是否存在异常，最后基于马氏距离构造调节因子，来调节观测噪声协方差矩阵和新息协方差矩阵，进而调整卡尔曼滤波的增益，以此减小动力学模型扰动和观测异常对滤波结果的影响。

1 GNSS/INS组合导航卡尔曼滤波模型

1.1 卡尔曼滤波模型

卡尔曼滤波是组合导航系统中大多数状态估计常用的方法，其采用递推的方法进行状态参数的预计算，使用前一时刻的状态估计值和状态估计均方误差矩阵来估计状态参数，再结合当前时刻的观测值，估计当前时刻的状态估计值和状态估计均方误差矩阵，按照“预测—修正”的形式进行递推，如此便能够实时估计系统中的状态参数。

卡尔曼滤波随机系统的动力学模型和观测模型为：

式中，Xk和zk分别是k时刻的状态向量和量测向量，Φk,k-1和Hk分别称为状态一步转移矩阵和量测矩阵，ωk-1和vk是互不相关的动力学模型误差向量和量测噪声向量，且两者都是零均值的高斯白噪声向量序列。

经过推导可以得到更为一般的状态一步预测和状态一步预测均方误差矩阵，即卡尔曼滤波的时间更新：

根据递推最小二乘估计方法，可以得到当前时刻的状态估计及其均方误差矩阵：

式（3）称为卡尔曼滤波的量测更新，式中第一个等式的Kk是在状态方差最小的约束准则下得到的，称为卡尔曼滤波的增益矩阵，从式（3）的第二个等式可以看出其能够调节状态预测值与观测值之间的权重。式（3）的第三个等式称为协方差量测更新的Joseph 稳定形式，这种形式可以提高系统解算的稳定性和鲁棒性。

1.2 自适应抗差卡尔曼滤波模型

在实际GNSS/INS 组合导航系统中，理论滤波模型与实际情况存在一定的偏差，随机动态系统的结构参数和噪声统计特性参数难以准确估计，导致先验协方差矩阵即状态一步预测均方误差矩阵的计算存在偏差，严重时甚至会导致标准卡尔曼滤波发散。在滤波过程中，滤波器发散时，误差协方差矩阵的理论计算值与实际估计相差较大，实际使用时一般采用量测新息构造的协方差矩阵，以此比较其理论计算值与实际估计。

量测新息的定义从式（3）中可以得出：

此时基于量测新息zk,k-1的协方差矩阵的理论计算值和实际估值分别为：

实际计算时，式中第二个等式中的m一般取1，此时=。由此可以构造如下基于量测新息的统计量：

其中，“tr”表示矩阵的迹。构造两段函数模型自适应因子如下：

其中，c为调整系数，可取1～1.5，最优值是1。

可以看出，自适应因子α会随着量测新息的增大而减小，但并不会减小为0。

当随机系统的动力学模型存在偏差且观测模型存在异常时，使用杨元喜在贝叶斯估计的基础上推导的M-LS 抗差滤波算法[13]。即对观测值序列进行M 估计、对状态参数进行LS（Least Square）估计。由此可得M-LS 估计的抗差滤波解的等价递推形式解为：

式中，¯Kk称为等价增益矩阵，可表示为：

量测噪声向量vk的协方差矩阵¯Rk的逆矩阵即为等价权矩阵¯Pk，因此在卡尔曼滤波中应用等价权抗差估计方法就可以得到参数的抗差解。而三段降权因子中IGGⅢ法能够充分考虑到观测数据的实际情况，因此使用IGGⅢ等价权函数构造等价权因子βk如下：

其中，k0和k1是阈值，k0的取值范围是2.5～3.5，k1的取值范围是3.5～4.5，表示第i个标准化残差，且zk,k-1(i)是量测新息的第i分量和其标准差矩阵对角线的第i个分量。

2 改进的自适应抗差卡尔曼滤波模型

式中，n表示统计量的自由度，α是显著性水平，表示显著性水平为α和自由度为n时的χ2临界值。观测信息故障检测的判别准则为：当(n)时，观测信息无异常；当γk＞时，观测信息异常。若观测值中存在粗差，则需要调节观测噪声协方差矩阵Rk。此时可以引入调节因子λk，可得调节后的观测噪声协方差矩阵¯Rk：

而此时的卡方检验统计量为：

将调节后的观测噪声协方差矩阵¯Rk代入写成函数形式后可得：

上式是关于λ的非线性方程，使用牛顿法进行迭代求解可得：

迭代i次后可以得到λ的解为：

基于上述理论，可以再引入一步预测观测协方差矩阵调节因子τk调节新息协方差矩阵Pzk,k-1，则调整后的新息协方差矩阵即出现观测粗差时的实际新息协方差矩阵可表示为：

其中，τk的表达式可以根据γk与(n)的关系解算得到，如下所示：

在下节实验中会使用自由度n为6 和显著性水平α为0.005 的卡方分布即(6)的临界值作为判定标准。最后得到卡尔曼滤波的增益为：

综上所述，在构建两个调节因子后，可以有效抑制观测值异常带来的影响。

3 算例分析

使用车载移动测量系统采集数据分析所提算法性能，车辆上装备GNSS 接收机和惯性测量单元IMU（Inertial Measurement Unit），可获取动态载体（实验车辆）在城市环境中的GNSS 数据和IMU 数据。实验中使用GNSS伪距单点定位数据计算得到的数据与IMU惯性导航数据经机械编排后得到的数据以松组合模式进行GNSS/INS组合，GNSS采样频率为5 Hz，IMU采样频率为200 Hz，组合采样频率为1 Hz，将IE（Inertial Explorer）软件差分后处理解算结果作为参考值。实验设置三种方案，分别是：1）GNSS/INS组合标准卡尔曼滤波（KF）；2）GNSS/INS组合自适应抗差卡尔曼滤波（ARKF）；3）GNSS/INS组合改进自适应抗差卡尔曼滤波（IARKF）。三种方案对应的卡尔曼滤波算法解算得到的结果分别与IE解算的参考值对比，得到的位置误差分别如图1、图2、图3 所示，三种方案所得误差的均方根如表1所示。

表1 三种方案均方根比较

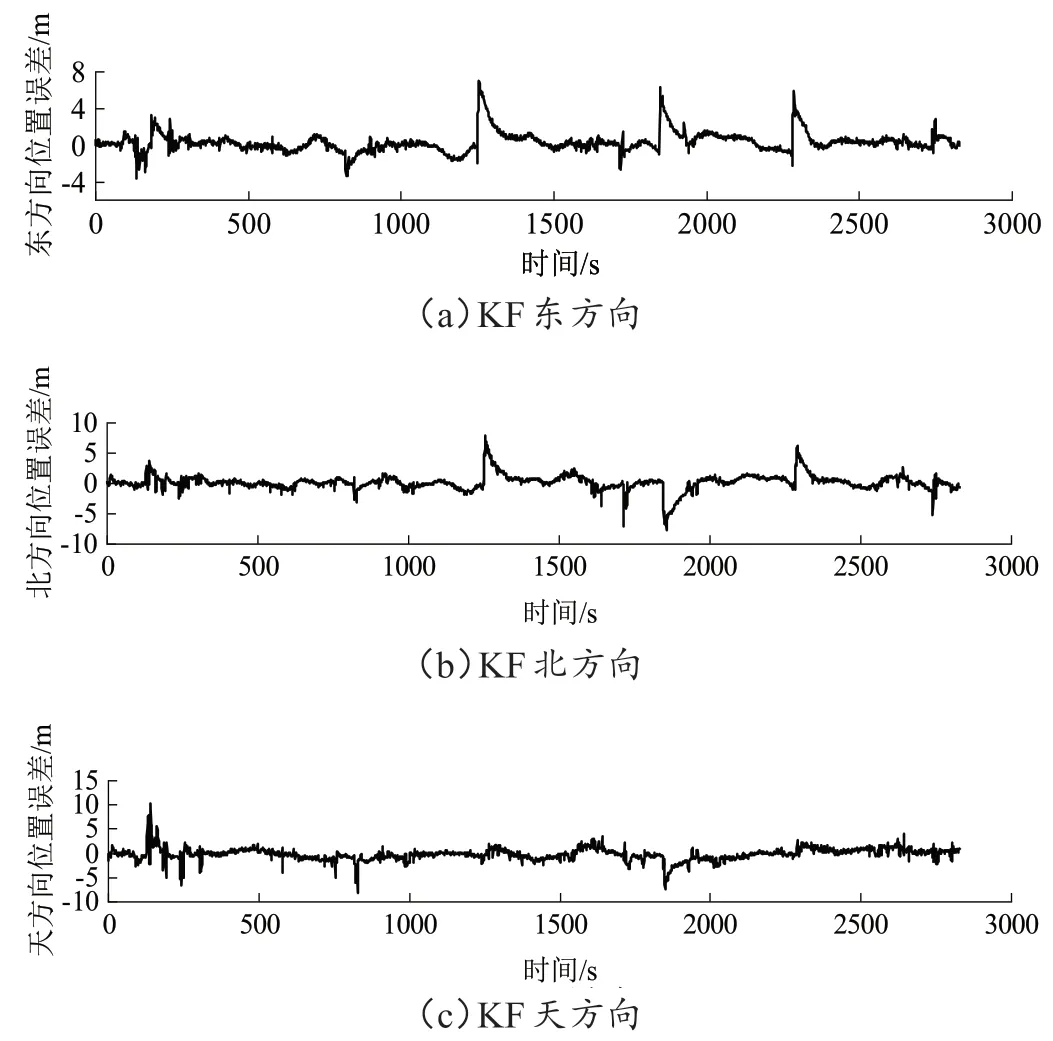
图1 标准卡尔曼滤波（KF）位置误差

图2 自适应抗差卡尔曼滤波（ARKF）位置误差

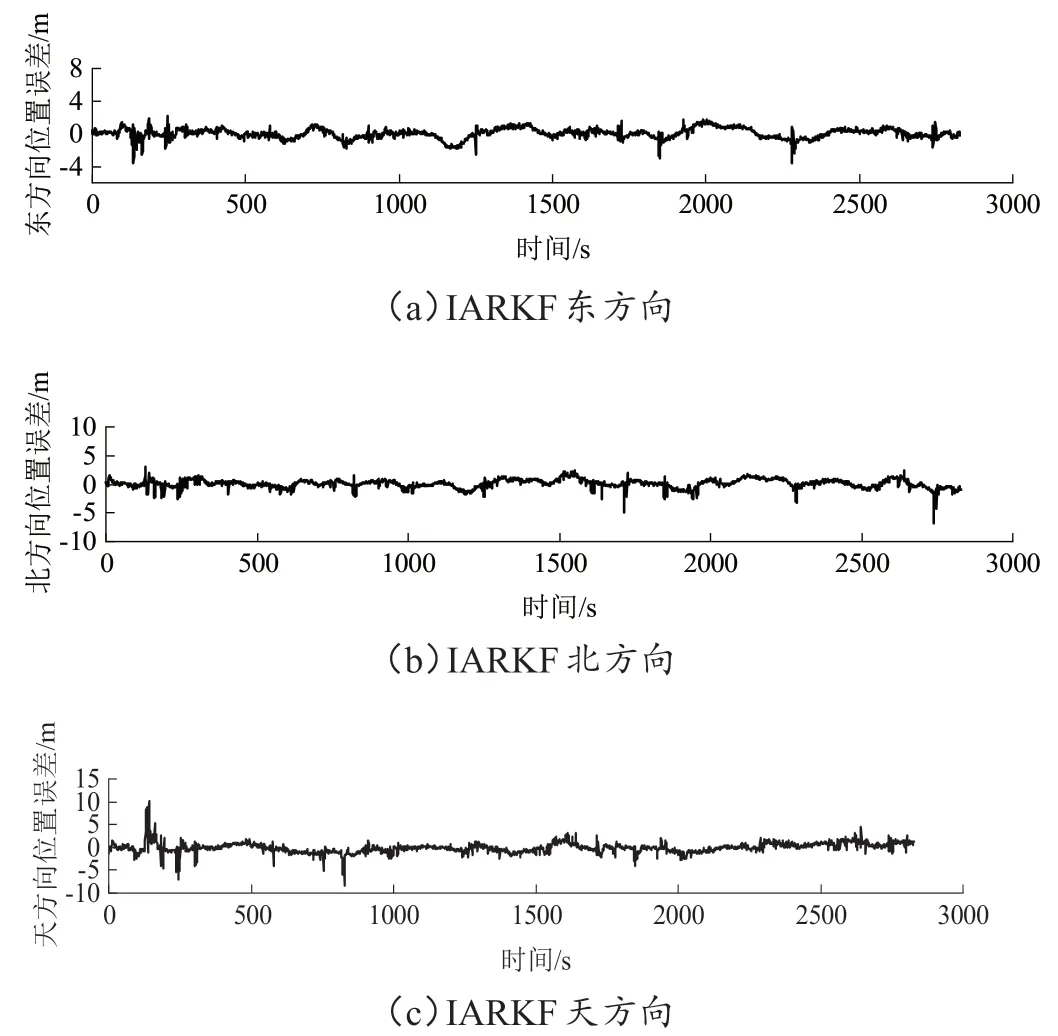
图3 改进自适应抗差卡尔曼滤波（IARKF）位置误差

对比图1、图2、图3可以看出，相比于方案2、3的ARKF 算法和IARKF 算法，方案1 的KF 算法在东方向、北方向、天方向三个方向的位置误差更大，说明方案2 和方案3 的算法可以有效抑制随机动态系统的不确定性对滤波结果的影响；从图2中可以看出方案2算法的定位结果仍然存在个别位置误差较大的点，而从图3 中可以看出方案3 算法将方案2 中误差较大的点平滑掉了，由此可见，方案3 算法能够对存在的观测值异常进行较为准确的判断调节，可以得到更准确的滤波结果，因此方案3算法要优于方案2算法。

对比表1 中三种方案误差的均方根，可以更直观地比较三种滤波算法的性能。当存在噪声干扰时，与方案1 相比，方案2 解算的位置误差均方根分别减小了0.340 3 m、0.159 8 m、0.134 2 m，方案3 解算的位置误差均方根分别减小了0.490 8 m、0.499 9 m、0.139 0 m。 结合上述对图1、图2、图3 的分析可知，在对GNSS/INS 组合导航数据进行抗粗差处理后，ARKF 和IARKF 解算得到的位置精度均高于 KF，其中IARKF 略有优势，在数据处理过程中通过假设检验对粗差进行判断，在模型异常时应用改进的自适应因子调节位置向量，有效避免了粗差和观测异常对系统带来的影响。

4 结语

针对城市环境中动力学模型异常扰动和GNSS 观测值存在粗差等因素影响，导致GNSS/INS 组合的数据滤波解存在误差，在给出的改进自适应抗差卡尔曼滤波算法中，使用量测新息构建马氏距离作为检验统计量，与卡方分布的临界值比较，以此判定观测数据是否存在异常。通过解算实际跑车数据对算法进行分析，结果表明改进的算法能够控制模型误差和测量异常值对导航结果的影响，提高GNSS/INS 组合导航性能。