仿生鳄鱼游动推进机制动力学分析*

冯创新， 蒋建平， 白宏磊， 何俊轩， 曾钦， 卓志钦

中山大学航空航天学院，广东 深圳 518107

鳄鱼是研制仿生水陆两栖机器人的重要仿生对象。鳄鱼在水中游动时，主要使用身体/尾鳍推进模式（梁建宏等，2002；王安忆等，2016），通过躯干和尾巴的周期摆动实现向前的游动。对于身体/尾鳍推进模式的机理有很多相关研究。Taylor（1952）采用静态流体理论，通过准静态逼近的方法建立了微小生物体的抗力水动力学模型。该模型着重考虑粘性力，而忽略了流体运动惯性力，适合雷诺数较小的情况。在Taylor 的基础上，Hancock 建立了大摆幅抗力理论，但也忽略了流体运动惯性力，只适用于雷诺数较小的水生生物（Taylor，2011）。Lighthill（1960）基于小振幅位势理论建立了鲹科鱼类推进模式的数学模型，并将空气动力学中的细长体理论用于鱼类小振幅摆动方式游动的水动力学分析，进一步提出了大摆幅细长体理论（Lighthill，1970）。Wu（1961）提出了二维波动板理论，将鱼体看作一块二维弹性板，分析了扁平月牙尾鱼类的游动规律。Chopra（1974）提出了一种可用于大摆幅、月牙形尾鳍推进的二维抗力理论。文献（Candelier et al.，2011）将细长体理论推广到三维情况，获得了作用于细长鱼体上的压力表达式和动量表达式。

鳄鱼在水中游动表现出隐匿性高、机动灵活、高效快速等卓越的游动特点，具有优异的水动力学特性。因此，国内外学者对于鳄鱼或仿鳄鱼机器人游动的水动力学进行了研究。王田苗等（2010）对仿鳄鱼机器人水中游动速度进行实验研究，分析了摆动频率、摆动幅值对游动速度的影响，但其运动模式和真实鳄鱼的游动有较大差距；游鹏（2022）基于中枢模式发生器控制方法，对仿鳄鱼机器人进行了水上运动控制仿真分析，该研究主要着眼于机器人的运动控制，但水动力学模型简单。Jia et al.（2015）建立了短吻鳄机器人的水动力学模型，但没有对其摆尾推进的动力学规律进行研究。文献（Seebacher et al.，2003）通过生物观察，研究不同体型鳄鱼的游动速度，分析了真实鳄鱼游动速度随摆幅和频率的变化规律。但目前对鳄鱼摆尾推进的动力学规律、推进效率和影响因素等的研究，还未见诸相关报道。针对鳄鱼水中摆尾游动问题，本文采用适合大Re问题的大振幅细长体理论，参考真实鳄鱼游动的姿态，用鱼体波幅包络线和行波曲线来描述鳄鱼游动的身体曲线，建立鳄鱼游动的运动学方程和动力学模型，用以揭示鳄鱼摆尾游动的规律，分析了鳄鱼稳态巡游过程中游动速度、加速度、推力功率以及游动效率随摆动频率、幅值和波长的变化情况，并给出游动效率随雷诺数（Re）和斯特劳哈尔数（St）的变化规律，为研制仿鳄鱼水陆两栖机器人提供理论参考。

1 动力学建模

1.1 鳄鱼摆尾的运动学模型

本文采用的鳄鱼模型为小型湾鳄，通过3D 扫描获得其物理模型，如图1（b）所示。该鳄鱼体长2 m、体宽0.35 m、体高0.17 m，尾巴长度为1 m。鳄鱼在水中稳态游动时，为了稳定和保持身体平衡，四条腿并拢在身体两侧（Manter，2005），如图1（a）所示（Allen et al.，2009）。将鳄鱼物理模型的外表面简化为连续曲面，以鳄鱼鼻子尖为坐标原点，建立固联于鳄鱼的随体坐标系（X，Y，Z）。其中，X轴为从头指向尾的方向，Y轴为体高方向，Z轴为鳄尾横向摆动方向，其简化模型和坐标系的示意如图1（c）所示。

图1 鳄鱼简化模型Fig.1 Simplified model of a crocodile

以鳄鱼体厚方向的对称中心线来描述鳄鱼游动的运动学关系，建立如图2所示的鳄鱼游动坐标系，(x，y，z)为绝对坐标系，以鳄鱼的体干中线弧长a作为拉格朗日广义坐标，设鳄鱼身体总长为l，在尾巴末梢点a=l，则体干中线上任一点的空间坐标可以用a表示为

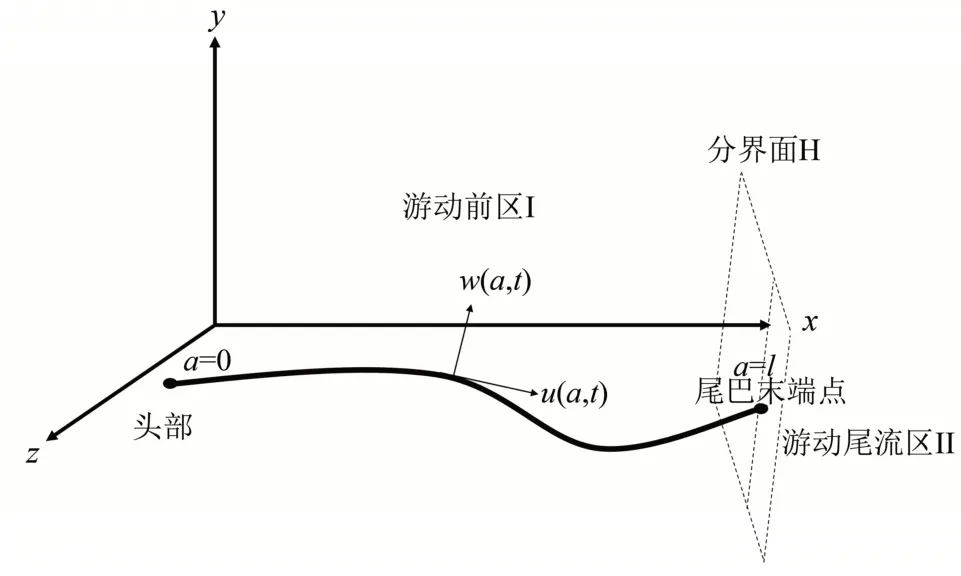
图2 鳄鱼游动坐标系Fig.2 The coordinate system for a swimming crocodile

假设鳄鱼体干中线上某点沿曲线的切向向量为，法向向量为，则体干中线上各点的切向速度为u(a，t)，法向速度为w(a，t)，体干中线某点的合速度矢量为。分界面H将鳄鱼游动的流场分为游动前区Ⅰ和游动尾迹区Ⅱ，且分界面H 始终垂直于切向速度u(a，t)，如图2所示。

根据笛卡尔坐标系和拉格朗日广义坐标系的空间几何关系，得

采用鱼体波幅包络线和行波曲线来描述鳄鱼游动的身体曲线（陈宏，2006）。在随体坐标系(X，Y，Z)中，鳄鱼在Y方向上没有运动，则鳄鱼游动时身体曲线表示为

其中Z(X，t)为身体横向位移，c为波幅包络线系数（等于鳄鱼的最大摆幅），f为摆动频率，λ为摆动波长。根据实验观测可知（Lindsey，1978），波幅包络线系数c= 0.2～0.5，摆动频率f= 0.5～1.5 Hz。当取c= 0.3、f= 0.5 Hz、λ= 1 m 时，鳄鱼的体干波动曲线族如图3所示，图中横轴表示体长。

图3 体干波动曲线族Fig.3 Body curves of a swimming crocodile

1.2 鳄鱼摆尾的动力学模型

鳄鱼体长一般是体厚的6 倍以上、体高的10倍以上。因此，鳄鱼可视为一个细长体，采用大振幅细长体理论（Lighthill，1971）建立其动力学模型。鳄鱼身体横向运动的虚质量很大，而纵向运动虚质量较小。因此，相对于法向速度w(a，t)的虚质量的动量，体干运动的切向速度u(a，t)对于体干某点的虚质量的动量，可以忽略不计。则单位弧长的动量矢量为

其中m(a)是鱼体某一截面的单位长度虚质量，可采用具有同样截面形状的水柱计算，即

其中ρ为鳄鱼周围流体介质的密度；S(a)为体干横截面的面积；β为无量纲的虚质量修正系数（陈宏，2006），取β= 0.95.将上述参数代入式（4）中，可得鳄鱼的虚质量分布如图4 所示。图4 中，在前腿体厚最宽处m(a)达到最大值，在头部顶端和尾巴末端m(a)为零。

图4 体干截面的虚质量分布Fig.4 The distribution of virtual mass from a crocodile nose to tail tipction

则

将式（6）-（7）代入式（5）中，得到鳄鱼所受周围流体的反作用力矢量

鳄鱼在水中游动的力学机理与惯性力、粘性力的相对大小有关，用Re=来表示两者的相对比例。其中，U表示游动速度，υ表示流体的运动粘度，l表示鳄鱼尾巴的最大摆幅。

鳄鱼在稳态巡游时，处于高Re范围，粘滞阻力相对很小，形体阻力占主导作用（Salazar et al.，2018）。此时，鳄鱼的四肢并拢于身体两侧，由鱼体主干产生形体阻力。因鳄鱼的物理模型是连续的且体干截面积变化率较小，为了简化计算，阻力D可以等价于具有相同Re的刚性体在相同流速所受到的流体阻力（夏丹等，2013），即

其中CD为流体阻力系数，ρ为周围流体介质密度，S为鱼体与周围流体的接触面积。且

设M为鳄鱼总质量，根据牛顿第二定律建立鳄鱼的动力学方程

将式（12）代入式（10）-（11），得

利用鳄鱼的有效功率和损耗功率来综合评价其游动效率。基于Froude 流体效率理论（王睿等，2016），瞬时有效功率为推进力P与游速U的乘积，瞬时损耗功率为尾迹区Ⅱ单位时间的动能ΔE，总瞬时输出功率等于有效功率与损耗功率之和，则鳄鱼的瞬时推进效率η为

一般认为水无粘性，则鳄鱼尾巴末端的邻近区域单位长度动能为尾巴末端的切向速度为u(a，t)|a=l，尾迹区Ⅱ的单位时间动能

2 鳄鱼游动效率的影响因素分析

鳄鱼自主游动过程中，身体主动变形对周围流体产生激励，使周围的流场发生变化，对身体产生反作用力（崔祚等，2020），游动速度和作用力逐渐达到稳态巡游的状态（白发钢等，2022）。本节将讨论鳄鱼游动过程中速度、加速度、作用力和游动效率的变化规律，分析摆动幅值、摆动频率等参数对游动性能的影响，揭示鳄鱼自主游动的力学机理，同时探讨Re和St对鳄鱼游动效率的影响。

2.1 摆尾频率、波长和幅值对运动特性的影响

初始时刻鳄鱼和流体均处于静止，鳄鱼身体逐渐摆动并加速到稳态巡游，分析该过程中摆动频率、波长和幅值对游动性能的影响。波长λ= 1 m，摆动幅值c= 0.3 时，不同摆动频率下鳄鱼游动过程中位移、速度和加速度如图5所示。

图5 c = 0.3，λ = 1 m时的位移、速度和加速度Fig.5 Displacement, velocity and acceleration of c = 0.3, λ = 1 m

在0.5、0.7、0.9 Hz 三种摆动频率下，鳄鱼游动速度从初始时刻经过大概12个周期达到稳态值，三种频率下的平均稳态游动速度分别为0.45、0.69、0.95 m/s；不同摆动频率下，鳄鱼加速度随频率的增加而增加。在0.9 Hz 时，加速度最大为0.41 m/s2；在0.7 Hz 时，加速度最大为0.24 m/s2；f= 0.5 Hz 时，加速度最大为0.11 m/s2；且加速度峰值随着时间增加而不断减小，最终达到稳定状态。

图6给出了鳄鱼稳态平均速度随摆动频率、最大摆幅和摆动波长的变化趋势。图7给出了稳态平均速度随摆动频率、最大摆幅和摆动波长的变化。可以得出结论，摆动频率对稳态平均速度的影响最大。在波长λ= 1 m，摆动系数c= 0.3 时，摆动频率从0.3 Hz 逐渐增加到1.2 Hz，稳态平均速度从0.24 m/s 逐渐增加到1.36 m/s，稳态平均速度和摆动频率几乎呈线性变化。在波长λ= 1 m，摆动频率f= 0.5 Hz 时，当最大摆幅从0.2 m 逐渐增加到0.6 m 时，稳态游动速度从0.30 m/s 逐渐增加到0.83 m/s，稳态平均速度和最大摆幅同样是几乎呈线性变化，但对稳态游动速度的影响不如摆动频率大。在摆动系数c= 0.3，摆动频率f= 0.5 Hz时，摆动波长λ从0.3 m 逐渐增大到2 m，稳态平均速度从0.26 m/s 逐渐变化到0.50 m/s，波长的变化对稳态平均速度的影响较小。λ从0.3 m 增大到1 m，稳态平均速度略微增大，λ从1 m 增大到2 m，稳态平均速度几乎没有变化。

图6 速度随摆动频率、幅值和波长的变化Fig.6 Ⅴelocity change with swinging frequency, amplitude and wavelength

图7 速度变化云图Fig.7 Ⅴelocity variation cloud map

2.2 摆动频率、波长、幅值对推进力的影响

图8 是f= 0.5 Hz，c= 0.3，λ= 1 m 时，鳄鱼瞬时作用力、瞬时作用力功率和瞬时游动效率随无量纲时间的变化趋势。随着鳄鱼尾巴开始摆动，瞬时阻力和推力都不断增大，同时呈现完整的周期性变化。刚开始时，瞬时阻力和推力的变化都较大，随着游动趋于稳定状态，瞬时阻力和推力的增大变缓，最终达到动态平衡。在此工况下，稳态游动的平均推力和平均阻力约为6.3 N，两者具有相同的频率，但阻力的波峰比推力滞后0.1 个周期。瞬时推力功率和阻力功率呈现周期性波动，瞬时推力功率在整个时间进程中始终大于瞬时阻力功率，达到稳态游动时的平均功率约为3 W。鳄鱼的瞬时游动效率在10%～99%之间周期性波动，鳄鱼的平均游动效率为60.33%。

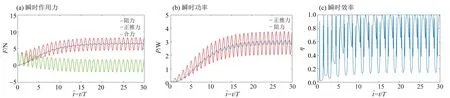
图8 f = 0.5 Hz，c = 0.3，λ = 1 m时的瞬时作用力、功率和效率Fig.8 Ⅰnstantaneous force, power and efficiency of f = 0.5 Hz, c = 0.3, λ = 1 m

鳄鱼游动过程中的推力功率和游动效率是很重要的水动力学参数。图9给出了稳态平均推力功率和平均游动效率随频率、波长和最大摆幅的等高线图。可以得出如下结论：1）频率是影响稳态平均推力功率的主要因素。对于给定的波长和最大摆幅，稳态平均推力功率随着频率的增加而增加，并且增加的梯度很大。在摆幅为0.6 m，波长为1 m 时，稳态平均推力功率从3 W 增加到最大200 W 左右；最大摆幅同样影响着稳态平均推力功率，对于给定的波长和频率，稳态平均推力功率随着最大摆幅的增加而增加，增加的梯度不如频率大。波长对稳态平均推力功率的影响最小。2）鳄鱼的平均游动效率随着频率、波长、幅值的变化而改变，总体在40%～64%的范围内变化；在频率为0.7 Hz，幅值为0.2 m，波长为1.2 m 附近取得最大的平均游动效率。这对于生物学的现象有一个良好的解释，当鳄鱼需要长时间游动时采用游动效率最高的方式，尽可能的节省体力；当鳄鱼对游速要求较高时，例如捕食时，通过增大摆动频率和摆动幅值，牺牲游动效率来获得较高的推进力和游速（Taylor et al.，2018）。

图9 平均推力功率和平均游动效率云图Fig.9 Average thrust power and average swimming efficiency cloud map

2.3 Re和St对平均游动效率的影响

Re和St对鳄鱼水中游动效率的影响如图10 所示，其中St=在图10中，鳄鱼的Re为3×104～1.4×106，St为0.52～0.85，鳄鱼的游动属于大雷诺数范围，惯性力远大于粘性力。鳄鱼游动过程中的非定常惯性力和惯性力处于同一量级，其非定常的作用力是不可忽略的。鳄鱼的平均游动效率随Re的增大先增大后减小，约在Re为3×105时取得最大值，这是由于随着鳄鱼的频率和幅值增加，其游动速度得到提升，Re也随之增大；当频率和幅值较小时，鳄鱼侧向摆动的功率较小，由游动前区作用于尾迹区的能量占比较大，此时在尾迹区中损耗的能量较多，平均游动效率较小；当鳄鱼处于最优摆动时，Re约为3×105，由游动前区作用于尾迹区的能量占比最小，此时在尾迹区中损耗的能量较少，平均游动效率最大；当鳄鱼的尾巴摆动愈加剧烈，Re继续增大，由游动前区作用于尾迹区的能量占比增大，此时在尾迹区中损耗的能量增多，平均游动效率不断减小。鳄鱼的平均游动效率随St的增大逐渐趋近于55%。这表明随着非定常惯性力占比的增大，鳄鱼平均游动效率最终趋于一个稳定值。基于大振幅细长体理论建立的水动力学模型下，这个稳定值和鳄鱼的外形结构以及运动学参数有关。

图10 平均游动效率随Re和St的变化Fig.10 The average swimming efficiency varies with Re and St

3 结 论

基于鳄鱼游动的运动学模型和Lightthill 细长体理论，本文提出了鳄鱼游动动力学模型，并系统研究了不同摆尾参数下鳄鱼游动的动力学特性及规律。主要结论如下：

（1）鳄鱼摆动频率、幅值和波长对鳄鱼游动加速度、稳态游动速度等都有影响，但摆动频率对加速度和稳态速度的影响最大。随频率、幅值和波长的增大，稳态游动速度逐渐增大、推力功率逐渐增加、功率损耗也逐渐增加。

（2） 存在一个最优的摆动参数。频率为0.7 Hz、幅值为0.2 m、波长为1.2 m 时，鳄鱼的平均游动效率达到最大值64%。

（3）Re和St对鳄鱼平均游动效率有较大影响，平均游动效率随着Re数的增大先增大后减小，约在Re=3×105时取得最大值，此时鳄鱼在尾迹区中损耗的能量占比最小。平均游动效率随St的增大逐渐趋近于55%。这表明随着非定常惯性力占比的增大，鳄鱼的平均游动效率最终趋于一个稳定值。