互通立交入口匝道大型车加速车道长度研究

李 敏，苏莉晓，李纳纳，陈婷婷

（山东省公路设计咨询有限公司，山东 济南 250102）

0 引言

据统计，在高速公路变速车道上发生的交通事故中，大型车事故率占20%以上[1]，由于合流时主线车速快，入口匝道的事故数占比较大，其中加速车道长度不足是导致事故率高的主要原因之一。同时由于大型车车身长且重、加速慢，合流时间长，合流所需要的加速车道长度要比小型车长。我国现行《公路路线设计规范》（JTG D20—2017）（简称“规范”）[2]中规定的不同设计速度下最小加速车道长度不能满足比功率较小、坡度较大时大型车的加速合流需求，存在一定安全隐患。因此分析互通立交入口匝道大型车交通特性，研究更加合理、人性化的大型车加速车道长度至关重要。

国内外很多学者对于变速车道长度及车辆合流特性进行了深入研究。Mohsen 等[3]通过对大、小型车加速行为进行研究，从而发现在合流区加速车道的长度不能满足大货车的加速要求，应结合大型车的运行特性增加加速车道的长度以保证车辆安全汇入。Weng 等[4]通过研究车辆合流影响因素，发现大型车汇入主线需要的可插入间隙大。张亚坤等[5]研究了大型车比功率、坡度与加速车道长度的关系，推导出符合我国互通立交车辆运行状况的加速车道长度推荐值。

1 合流影响区交通特性研究

如图1 所示，合流影响区指主线车道1、车道2及加速车道合流鼻上游150 m，下游760 m 的范围[6]。

图1 合流影响区范围示意图

1.1 车头时距分布模型

不同车流量服从不同的车头时距分布模型。受车辆加速合流行为的影响，车道1 在整个合流影响区不同区段的车流量不同，因此车头时距分布模型不同。合流影响区上游，车辆行驶相对自由，车道1 车流量分布在0～250 veh/h 范围内，此时车头时距服从1 阶爱尔朗分布；在合流影响区内及下游，受车辆合流行为的影响，车道1 车流量增加，基本保持在250～500 veh/h 范围内，此时车头时距服从2 阶爱尔朗分布[7]。

1.2 可插入间隙特性

可插入间隙是指匝道车辆顺利汇入主线时利用的最小车头时距[8-9]。合流车辆从匝道经过加速车道驶入主线，在行驶过程中跟随道路条件及周围车辆行驶状况来适当调整车辆行驶的速度，寻找主线合适的可插入间隙。大量的调查统计资料和研究表明，大型车可插入间隙一般在4.5～5 s[10]。

2 加速车道长度计算模型及关键参数取值

2.1 计算模型

经实地调研发现，当前大多数互通立交入口匝道采用单车道平行式，因此本文研究的加速车道形式为单车道平行式。如图2 所示，加速车道长度包括加速段L1、等待段L2和渐变段L3，净加速车道长度L12=L1+L2。

图2 单车道平行式加速车道长度示意图

根据如图2 所示的车辆在加速车道每段的驾驶特性，结合1.1 节分析，本文以二阶爱尔朗车头时距分布模型为基础，建立合流车辆在坡度-2%≤i≤2%的加速车道长度计算模型。

坡度-2%≤i≤2%的的大型车加速车道长度计算模型如下：

式中：vn为汇流鼻初速度，km/h；vm为汇流点末速度，km/h；u 为车辆行驶速度，km/h；ai为车辆加速度，m/s2；a 为车辆平均加速度，m/s2；a0为车辆重力分力沿坡面产生的反向加速度，m/s2；tw为平均等待时间，s；t 为横移时间，s。

2.2 模型关键参数取值

2.2.1 汇流鼻初速度vn

图3、图4 为实测坡度-2%≤i≤2%的互通立交汇流鼻平均运行速度[7]。结合车辆实际汇流情况，以汇流鼻平均运行速度作为加速车道长度计算的汇流鼻初速度。

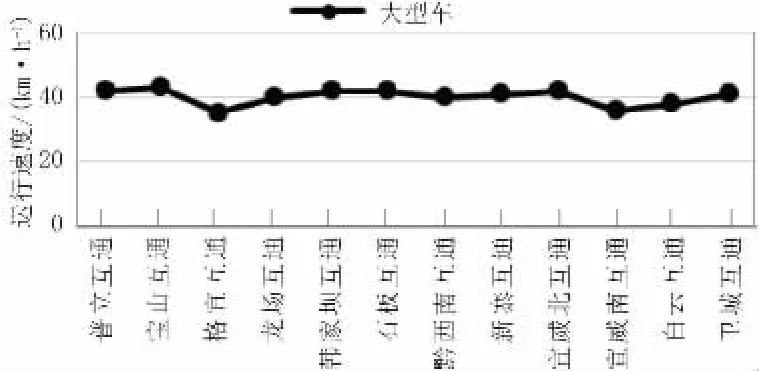
图3 匝道设计速度40 km/h 的汇流鼻平均运行速度曲线图

图4 匝道设计速度60 km/h 的汇流鼻平均运行速度曲线图

结合实际调研数据并参考规范等相关规定，推荐大型车在坡度-2%≤i≤2%的汇流鼻初速度的取值如表2 所列。

表2 汇流鼻初速度取值表

2.2.2 汇流点末速度vm

参考日本、美国相关规范及国内观测统计资料[11]，推荐主线设计速度80 km/h、100 km/h、120 km/h 时的汇流点末速度取值，见表3 所列。

表3 汇流点末速度取值表

2.2.3 车辆加速度ai

结合汽车理论，以东风EQ-140 车型为研究对象，分析大型车在爬坡过程中的受力，可知车辆在坡度为i 的坡道上行驶时，车辆主要受力有空气阻力Fw、坡度阻力Fi、滚动阻力Ff、加速阻力FI，根据汽车运动方程可知[7]：

通过计算可得：

式中：A 为车辆迎风面积，m2；v 为行驶速度，m/s；a为加速度，m/s2；i 为纵坡，%；G 为车辆总重力，N；P为发动机功率，kW；M 为车辆总质量，kg；P/M 为比功率，kW/kg；ηT为传动系统的机械效率；Ca为空气阻力系数；δ 为惯性力系数；f 为滚动阻力系数；g 为重力加速度，m/s2[7]。

根据公式（3）可以看出，大型车加速度与车辆的速度v、坡度i 及比功率P/M 有关；车辆在加速行驶过程中，随着坡度、比功率的变化，加速度也在发生变化。

3 大型车加速车道长度

3.1 不同坡度下大型车加速车道长度

3.1.1 加速段长度

由公式（3）分析可知，大型车的加速度是实时变化的，因此通过积分计算方法对加速车道长度进行计算，见公式（4）。

式中：L1为加速段长度，m；v 为运行速度，km/h，取值范围为vn～vm；vn为汇流鼻初速度，km/h；ai为加速度，m/s2，2%≤i≤2%；式中其它字母代表的含义同公式（3）。

以实际调研中的东风汽车EQ-140 货车为例，公式（4）中参数取值见表4 所列。

表4 汽车运动方程中参数取值表

通过表4 中参数计算出东风汽车EQ-140 的比功率为10 kW/t。结合实际情况，当坡度小于0 时，有利于车辆加速，所需加速车道长度比上坡时小。因此以此车型为例，利用MATLAB 软件编程，绘制出比功率10 kW/t，坡度0%≤i≤2%时的大型车的速度与加速段长度的关系曲图线见图5 所示。

图5 坡度0%～2%的大型车运行速度- 加速段长度曲线图

从图5 中可以看出，坡度0%≤i≤2%时，坡度越大，车辆加速所需的加速车道长度越长。由于坡度0%～2%的加速段长度相差很小，为保证大型车行车安全，计算出坡度i=2%时大型车需要的加速段长度作为坡度-2%≤i≤2%时的大型车加速段长度的推荐值。具体推荐值如表5 所列。

表5 坡度-2%≤i≤2%的大型车加速段长度表

3.1.2 等待段长度

通过1.1 节分析可知，合流影响区范围内车道1的车头时距服从2 阶爱尔朗分布。车头间距至少为一个车身长加上一定的安全车距。因此需要对2 阶爱尔朗分布进行修正。修正后的2 阶爱尔朗分布的概率密度函数为：

车头时距大于等于t 的概率为：

汇流车辆在等待m 个不可插入间隙后汇入主线的概率为：

则平均等待个数为：

该级数绝对收敛：

则平均每个间隔的等待时间为：

平均等待时间等于H 与n 的乘积，所以有：

车辆在等待段以汇流点末速度vm匀速行驶，因此等待段长度L2为：

式中：Qmax为单车道二级服务水平最大交通量；λ 为车辆单位时间的平均到达率，λ=Q/1800，veh/s；τ 为目标车道最小车头时距，τ=1800/Qmax；n 为平均等待个数，个；tw为平均等待时间，s；tc为可插入间隙值，s，大型车的可插入间隙值一般取4.5～5 s[7]。

具体的大型车等待段长度计算结果如表6 所列。

表6 大型车等待段长度表

3.1.3 渐变段长度

车辆在渐变段以汇流点末速度vm匀速行驶，因此渐变段段长度L3为：

式中：t 为横移时间，s，取4 s.

综上，经过计算，纵坡-2%≤i≤2%的大型车加速车道长度L 如表7 所列。

表7 坡度-2%≤i≤2%大型车加速车道长度表

从表7 中可以看出大型车加速过程需要的单车道加速车道的长度比《规范》中规定的长。大型车在v匝道=40～50 km/h 时需要的加速车道长度是《规范》中规定长度的1.2～1.8 倍。

3.2 不同比功率的大型车加速车道长度

通过公式（4）、公式（12）及公式（13）可知，大型车加速段长度与比功率成反比，大型车等待段、渐变段长度与比功率无关。通过MATLAB 编程，研究大型车在不同比功率下加速段长度和比功率的关系，以坡度i=2%为例，计算出比功率为8～12 kW/t 的大型车加速段长度，见表8 所列。

4 结 论

计算结果发现：（1）主线设计速度一定时，匝道设计速度越小，需要的加速车道越长。（2）匝道设计速度一定时，主线设计速度越大，需要的加速车道越长。（3）考虑到大型车加速车道长度受坡度的影响较大，对大型车从坡度2%≤i≤2%建立相应加速车道长度计算模型，计算出在坡度-2%≤i≤2%时，大型车在匝道设计速度=40～50 km/h 时需要的加速车道长度是《规范》中规定的长度的1.2～1.8 倍。（4）一定坡度下，比功率越大，车辆加速性能越好，合流需要的加速段越短，加速车道长度越短。