Numerical analysis of moving train induced vibrations on tunnel,surrounding ground and structure

Swati Srivastav, Sowmiya Chawla and Swapnil Mishra

1.Department of Applied Geophysics, Indian Institute of Technology (ISM), Dhanbad 826004, India

2.Department of Civil Engineering, Indian Institute of Technology (ISM), Dhanbad 826004, India

3.Department of Mining Engineering, Indian Institute of Technology (ISM), Dhanbad 826004, India

Abstract: This study is focused on the effect of vibration induced by moving trains in tunnels on the surrounding ground and structures.A three-dimensional finite element model is established for a one-track railway tunnel and an adjacent twelvestorey building frame by using commercial software Midas GTS-NX (2019) and Midas Gen.This study considered the moving load effect of a complete train, which varies with space as well as with time.The effect of factors such as train speed, overburden pressure on the tunnel and variation in soil properties are studied in the time domain.As a result, the variations in horizontal and vertical acceleration for two different sites, i.e., the free ground surface (without structure) and the area containing the structure, are compared.Also, the displacement pattern of the raft foundation is plotted for different train velocities.At lower speeds, the heaving phenomenon is negligible, but as the speed increases, both the heaving and differential settlement increase in the foundation.This study demonstrates that the effect of moving train vibrations should be considered in the design of new nearby structures and proper ground improvement should be considered for existing structures.

Keywords: moving train load; tunnels; vibration effect; finite element method (FEM); wave propagation

1 Introduction

In recent decades, the increase in population density has necessitated the development of more sophisticated and efficient modes of transportation.As population density rises, the demand for transportation infrastructure rises, but the land surface area continues to shrink,making it more challenging to construct surface railway tracks.Therefore, the development of underground tunnels can serve as a solution to the problem of limited land usage.Nevertheless, underground traffic has its own unique complexities.

India currently operates semi-high-speed trains with an operational speed between 150 km/h and 180 km/h and aims to upgrade its rail transit structure to highspeed trains, whereas high-speed trains around the world operate at speeds greater than 300 km/h.As train speed increases, the vibrations along railway lines become a major concern, as they will propagate through the soil layers to the surface of the ground.If this vibration exceeds the limit, it will have the potential to affect the existing structure’s foundation and will also influence the design of newly planned structures.Lamb’s groundbreaking research compared the response of isotropic and homogeneous elastic half-spaces to different harmonic and impulsive loads (Kourossiset al., 2014).Three types of waves are generated when an oscillating point load is applied to an elastic half space.Rayleigh waves (surface) attenuated at a rate inversely proportional to the square root of the surface’s distance in the far field.The other two were body waves, namely the primary wave and the shear wave, which attenuated at a rate that was inversely proportional to the distance from the surface (speed in the orderCP＞Cs＞Cr).The Rayleigh wave is typically the dominant surface wave.However,the concept of wave propagation is generally applicable to an elastic half-space, whereas in the real world the ground consists of multiple soil strata.Consequently,if the elastic and linear behavior of each soil stratum is maintained, it is possible to extend this method to each layer or soil stratum, which is defined by its Young’s modulusEi(or shear modulusGi), Poisson’s ratiovi,densityρi(ibeing the layer index), and damping ratio.

The vibration was transmitted from the underground tunnel entrance to the superstructure via the contact between the train wheel and rail.Figure 1 is a graphical representation of the wave transmission through the soil layers caused by the movement of the train in the underground tunnel.

Fig.1 Propagation of ground vibration into the building from underground tunnel railway (FTA, 2006)

The potential of the transmitted wave is highly dependent on the dynamic properties of the soil layers and the rail wheel contact characteristics (Gutowskiand and Dym, 1976).The train tunnel system’s vibration excites the ground surrounding the tunnel and propagates through the soil layers to the foundations of buildings and other systems on the ground surface.The effect will become more hazardous if the natural frequency of the structure exceeds the wave frequency, i.e., if the structure is in a resonance state.

There are various methods such as field experiments,analytical methods, empirical prediction models and numerical simulations that have been used by many researchers to predict the ground vibration responses in the past.Most of the initial key research on ground borne vibration has been done by field experiment (Pan and Xie,1990; Vadilloet al.,1996; Degrandeet al.,2006;Fenget al.,2021) and empirical prediction (Kurzweil,1979; Melke, 1988; Trochides, 1991; Hoodet al.,1996)because of their reliability and simplicity.But in these methods, the parametric study is not easily performed.To overcome this limitation, studies have been carried out by analytical method to study the railway induced vibration phenomenon (Krylov and Ferguson, 1994).The effect of quasi static load is represented by the analytical beam model, in which the load is transmitted to soil through the rail and sleeper (Krylov and Ferguson, 1994).Metrikine and Vrouwenvelder (2000) extended the model to study the soil-track interaction.This method generally requires complicated calculations, and this drawback was overcome by the numerical method based on finite element, where the moving train is more conveniently simulated and train-induced vibration and propagation could also be predicted.Yanget al.(2007) studied the ground vibrations due to underground trains considering soil-tunnel interaction and gave a brief review of the research works on ground vibrations caused by trains moving in underground tunnels.Yang and Hung (2008)developed a 2.5D finite or infinite element approach for assessing the wave propagation problem caused by underground moving trains.Hung and Yang (2010)presented the details for implementing the 2.5D finite/infinite element approach.Linet al.(2016) presented a procedure for the seismic analysis of underground tunnels by 2.5D finite/infinite element approach.Linet al.(2017) studied the 2D seismic response of horizontally aligned twin tunnels by using the finite/infinite element approach.Feiziet al.(2022) studied the seismic ground amplification induced by box-shaped tunnels.Yanget al.(2017) did a comparative study of 2D and 2.5D responses of long underground tunnels to moving train loads.The dynamic response of a tunnel embedded in layered foundation soil with different saturated conditions have been analytically evaluated by Diet al.(2022).The train movement simulation and calculation of ground surface vibration induced by train movement was studied on Tehran’s subway tunnel by Realet al.(2015).Numerical analysis of ground surface vibration induced by underground train movement was also performed by Nejatiet al.(2012).Centrifuge modeling of ground-borne vibrations induced by railway traffic in tunnels was also studied by Yanget al.(2022).

Zhanget al.(2022) studied the dynamic response analysis of a multiple-beam structure subjected to a moving load.Most of the previous researchers studied the 2D and 3D numerical model for surface railway track and surrounding structures (Zouet al., 2016), but very few models have been developed with an underground structure (Hong and Liu, 2006; Wanget al., 2013) to study the direct effect of tunnel vibration on the surface structure and its foundations.

In this study, a parametric study is carried out using a finite element method (FEM) based numerical model that included tunnel, soil layers, and ground structure with a pile raft foundation was generated by using commercially available software Midas GTS-NX (2019)and its direct effect has been studied on the ground surface and on nearby structure and its foundation.The Mohr-Coulomb elastoplastic constitutive model has been used to simulate the soil behavior.The viscous boundaries have been considered to ensure that there was no reflection of waves from the boundaries and Rayleigh damping was also simulated to ensure reliable results.

2 Analysis details

2.1 Tunnel cross-section

A circular tunnel of diameter 6.26 m was modeled at a depth of 16.87 m from the ground surface.The Tunnel opening was supported with a reinforced concrete lining with a thickness of 0.28 m.The elastic modulus of reinforced concrete (RC) liners,Ecwas 3.16 × 107kPa and the Poisson’s ratio was 0.15.One railway tracks Indian gauge 1435 mm embedded in the concrete slab rested on a concrete layer inside the bottom of the tunnel was considered in this study (Fig.2).

2.2 Soil properties

Delhi is located in Zone Ⅳ of India’s earthquake zoning maps.This study analyzes a typical section of the Delhi Metro Rail Corporation (DMRC) tunnel between the Rajiv Chowk and Patel Chowk metro stations.The DMRC tunnel was excavated through deposits of alluvium, also known as Delhi silt.In this study, the engineering properties of alluvium were taken from Yadav (2005) and Soni (2015), and the variation in elasticmodulus of Delhi silt with depth is summarized in Fig.3 and Table 1.Each of layers 1, 2,and 5 is 10 m thick, while layers 3 and 4 are 15 m thick(Fig 2.2.1).The in situ unit weight,γbulk, and saturated unit weight,γsat, were assumed to be 18 and 20 kN/m3respectively for all layers (layer 1, layer 2, layer 3, layer 4,layer 5 (Fig.3).During the analysis, the entire soil domain was considered to be dry.Cohesioncof Delhi silt was assumed to be zero (cohesionless silt), and the values of friction angle (φ) and dilatational angle (ψ)were determined to be 35° and 5°, respectively (Singhet al., 2017).Damping in the soil and RC liners was accounted for as 10% and 2%, respectively (Singhet al.,2017).

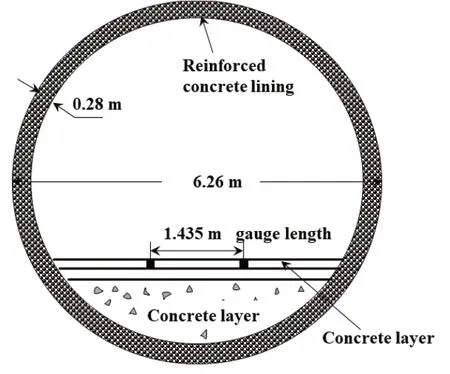
Fig.2 Tunnel section (after Real et al., 2015)

Fig.3 Geometry of nominal model (front view)

2.3 Structure specification

A twelve-storey building with a pile raft foundation and structure of M20 concrete, column with cross-section 0.45 m × 0.45 m and beams of cross-section 0.3 m × 0.2 m,nine piles of diameter 1 m and length of 10 m embedded in raft of thickness 0.3 m was considered for this analysis.The complete structure was modelled at a distance of 25 m from the center of the ground surface.

2.4 Vehicle characteristics

In this study, the effects of moving train were studied for which EL- 18 standard, 6 car vehicle, axle load 180 kN,having 24 axels moving in the metro tunnel has been considered.The train axle and other dimensional details areL= 17.7 m,a= 2.1 m,b= 10 m (Fig.4).The train load varies with time as well as space, and the load vs.time graph is shown to better represent its initial state,i.e., the starting point of the railway track (Fig.5).

3 Three-dimensional numerical modelling

3.1 Geometric modelling

Consideration is given to the three-dimensional(3D) modelling of a metro tunnel embedded in five distinct soil strata with a twelve-storey building at the ground surface.The width of the model to be taken was 140 m in the globalX-direction, the total depth in the globalY-direction was 60 m, and the depth of the soil consisted of five soil layers (Fig.3).The modified constitutive Mohr-Coulomb model and the elastic model were used to simulate the behavior of the soil and structural component, respectively.Water depth was not taken into account when calculating the total soil depth.Hatzigeorgiou and Beskos (2010) have observed that a minimum of 6-10 nodes per wavelength must be present in a model for it to generate reliable results.This studyutilized 12 noded hybrid elements to discretize the entire domain (Fig.6).

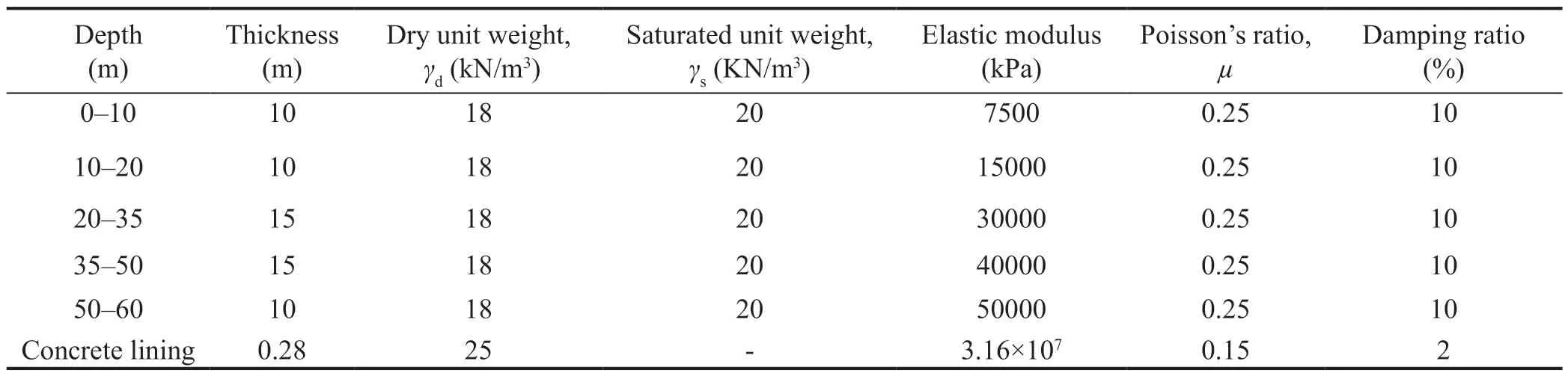
Table 1 Material properties

Since the hybrid element is a combination of tetrahedral and hexahedral elements, it must utilize the properties of both types (Midas, 2019).As hexahedral elements produce more precise results, tetrahedral elements are best suited for stress-concentrated regions.In this study, the tunnel openings fall within a region of stress concentration; therefore, hybrid elements were used to improve precision.

3.2 Load application

The effect of the moving train was considered in this study despite the fact that quasi static load, as in dynamic load inertial force, is considerable which causes structure to vibrate.Conversely, in quasi static load, the inertial force consideration is minimal.However, it has been observed that the results obtained are similar at low strain.The total axel load of 180 kN was divided into two halves and acts on the nodes of the two the parallel rails.The effect of 24 axels has been considered as moving simultaneously at the speed of 60 m/s in the nominal model.

Fig.4 Geometry of wheel axle load distribution of a train

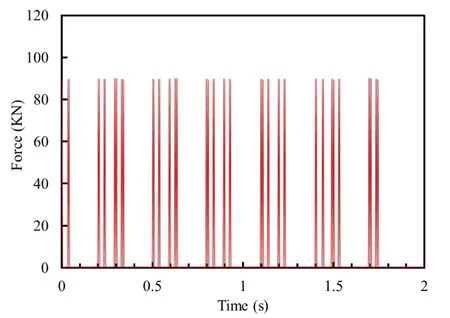
Fig.5 Moving train load

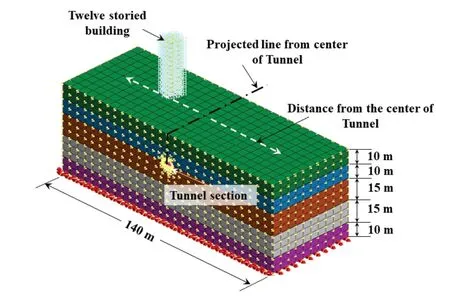
Fig.6 Isometric view of Discretized Nominal model

3.3 Analysis

The eigenvalue analysis was performed first to obtain the main vibration mode or the characteristic frequencies and the period of the given system.Eigenvalue extraction using normal mode analysis has been performed and formulation of the same, neglecting the damping, have been shown in Eq.(1).

where,Mis the mass matrix,Kis the stiffness matrix,uis the displacement vector andüis the second derivative of the displacement vector (acceleration vector).

Whereas in the linear system free vibration is represented by the harmonic function (Realet al.,2015)

From Eq.(2),φiis the eigen vector associated with the mode shape of theωinatural frequency.By combining Eqs.(1) and (2), Eq.(3) can be obtained.Equation (3)has been used for the eigenvalue analysis herein.

As this eigenvalue problem is dependent on the mass and stiffness of the system and if any static load is to be considered, these loads should be converted into masses.In this study, all the floor loads on the buildings were converted into masses to be considered in the eigenvalue analysis.

Equation (3) is computed fornvalues of the natural circular frequencies of the systemωiand eigenvectorsφi.Natural frequenciesfiwere also computed by Eq.(4).

For analysis purposes, the elastic boundaries at the surface of the soil layers were provided; their stiffness is calculated as follows:

where,E0is the elastic modulus of soil andais a coefficient that depends on the test conditions.

The subgrade reaction modulusKv(=Kh) is recalculated using the computedK0v(see the online help manual of Midas GTS-NX (2019)).

The predominant periods obtained from the eigenvalue analysis were 1.682663 s and 1.61263 s.

These predominant periods were further utilized while performing linear time history analysis and ignoring the response from the moving train load vibration.Linear time history is solved by using Eq.(7)

where,Mis the global mass matrix,üis the vector of acceleration,Cis the damping matrix,uis the vector of velocity,Kis the stiffness matrix,uis the vector of displacement andFa(t) is the time dependent force vector.Where,MandKdepend on the material and stiffness properties, butCis not directly related to these properties.The damping effects in the linear time history analysis were applied to the damping matrixCin the following form:

where,αis the mass proportional damping coefficient,βis the stiffness proportional damping coefficient,Mis the mass matrix of the element,Kis the stiffness matrix of the element andBis the damping matrix due to the damping element (damper) (Midas GTS-NX (2019)manual).

The damping ratio is then calculated by orthogonal transformation of the damping matrix and results in Eq.(9)

in this equationξi,ωiare the damping ratio and the frequency of the system..

Here,αandβwere calculated by using the predominant frequencies obtained from eigenvalue analysis.While considering the dynamic analysis,boundaries of the soil surface are such that it should not reflect the waves generating during the movement of the train.Therefore, to counteract this phenomenon, viscous boundaries were assigned at the surface of the soil layers to make it act as infinite boundaries.The coefficient of viscous boundaries stiffness was computed with the help of input data such as elastic modulus and Poison’s ratio,etc.

3.4 Validation of literature

An attempt was made to validate some of the significant findings from the previous literature and to ensure the reliability of the software used in this study with respect to the moving train load analysis.The insitu vertical vibrations that were generated due to the movement of vehicle “RENFE CIVIA 465” running at a speed of 55 km/h in the tunnel, located in a Spanish commuter train line near Madrid, has been observed at the middle of the slab (Realet al., 2015).The same had been attempted in this study for the validation of the vertical time history.The comparison of recorded vertical acceleration in the study of Realet al.(2015)and calculated acceleration in the validation is shown in Fig.7.The average difference of amplitude has been observed as 10.3 %.

3.5 Parametric study

A comprehensive parametric analysis was carried out to examine the effects of various parameters on the ground surface vibration, such as the fluctuation in train speed, the depth of the cover, and the elastic modulus.Engineers can improve their knowledge of complex models through the use of a parametric study.

The analysis has been performed for the speeds,i.e., 20, 40, 60, 80, and 100 m per second.On the other hand, because there was a large amount of data, and because an effort was made to simplify the study, it was condensed.Some of the outcomes, such as horizontal acceleration and pile deformation, have been compared for very low, medium, and very high speeds, which are 20, 60, and 100 m per second, respectively.The analysis was performed at a shallow depth of tunnel (at low overburden pressure); i.e., at 6 m from the ground surface,which was 16.87 m in nominal conditions.The results were also observed after changing the elastic modulus of the upper two layers to the lower value (Table 2).

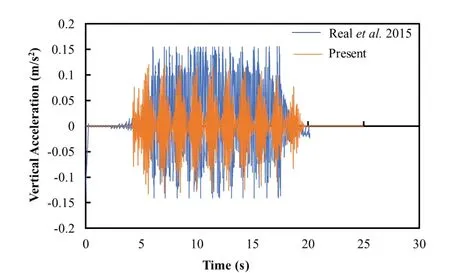
Fig.7 Comparison of vertical acceleration at middle of slab

Although the load speed of 60 m/s (equivalent to 216 km/h) and 100 m/s (equivalent to 360 km/h) is common for a surface high-speed train, it is too high for an underground (subway) train and the variation of the stress wave speed and load speed (c) affects the propagation of vibration in the media.It has been observed in past studies that in the sub-critical case,c＜Cr(Cr= the velocity of Rayleigh wave), since the velocity of the wave is larger than that of the moving load, the stress waves propagate to the observation point before the load arrives.For the super-critical case,c＞Cr, the reverse is true (Yanget al., 2019; Hung and Yang, 2010;Linet al., 2016, 2017).The velocity of Rayleigh waveCr, primary waveCp, and secondary wave was found to be 50.4, 54.77 and 94.86 m/s, respectively, in this study.It has been found that the load speed of 60 m/s and 100 m/s is lying in the super-critical case asc＞Cr.Therefore, the motivation for including such a high speed in this study is to account for future development.The purpose of this analysis is to determine how the ground will react when a train travelling at such a high speed is brought into a real-world situation or the extent to which speed can be increased.

4 Results and discussion

Generally, humans are more sensitive to velocity and acceleration rather than displacement during vibration.Accordingly, in this study, an attempt is made to depict the level of vibrations.To examine the human suffering and the factor of vulnerability created by ground vibrations, two methods were adopted: (1) particle peak velocity (PPV), (2) root mean square velocity (Vrms).Vrmsprovides the result from the entire velocity time history and is computed as:

The vibration level in decibels was calculated using thisVrmsvalue:

where,Lvis the velocity level in decibels (dB),Vrefis the reference velocity amplitude and its value is generally adopted as equal to 1×10-5in/s in the American standard and 5×10-5mm/s in all other places (Nejatiet al., 2012)accordingly,Vrefwas assumed as 5×10-5mm/s.Table 3 shows the human and structural response to different vibrations levels.Here three models were considered,Model 1: with all nominal conditions (Table 2), Model 2:overburden pressure height is reduced to 6 m from 16.87 m, and Model 3: the elastic modulus of the upper two layers has been reduced,E1(Layer 1) was reduced to 1.5 MPa andE2(Layer 2) was reduced to 15 MPa.Horizontal acceleration, vertical acceleration,and vertical displacement of the raft was obtained for different train speeds for Model 1, Model 2 and Model 3.Accordingly, the results have been observed and are discussed.

4.1 Velocity level attenuation

The influence of train speed on attenuation of vibrations at various distances from the center of the ground surface were studied for three different models(Fig.8).The increase in train speed was accompanied by the increase in velocity level.The velocity level was attenuated at a higher rate for a train speed of 40 m/s,whereas the attenuation rate decreased after 20 m from the middle of the ground surface for a train speed of 20 m/s in Model 1.From the results, it has been observed that the depth is inversely proportional to frequency, where high velocity waves dissipated their energy while traveling through the soil medium at a higher rate and traveled less distance.Conversely, the low velocity waves lose energy at a slower rate, so their effect persisted for a longer distance from the origin.This trend became more intense for Model 2, where at some distance it matched the rate of attenuation for a 60 m/s train speed.A different trend in velocity attenuation was observed for Model 3, where the stiffness of the soil relaxed the damping to a higher degree.From Fig.8(c), it is seen that the values of the velocity level are substantially lowerwhen compared to other models.The velocity level was attenuated at a faster rate for the 20 m/s train speed,whereas the attenuation rate was observed to be similar for all other train speeds.The train speeds of 40 m/s and 60 m/s exhibited almost the same velocity level in this case.

Table 2 Parameters of present study

Table 3 Typical ground-borne vibration level (FTA, 2006)

It has further been observed that at higher velocity,there was gap in velocity attenuation rate and the attenuation rate exhibited a similar trend at higher train speeds.Hence, the trend of the velocity attenuation at different distances from the center of the metro tunnel is a key factor to observe for safety and reduced the factor of vulnerability for the inhabitants living in that region.The velocity level should be in the prescribed limit as suggested by the FTA (Federal Transit Administration)2016 guidelines (Nejatiet al., 2012).From Fig.8, it is seen that the velocity level reached 83.1 dB, 88 dB and 89.09 dB for the three models.It was also observed that these velocity levels were greater than the prescribed limit suggested by FTA (2006), under human/structural response to infrequent 80 rapid transit the upper range is 80 dB (Table 3).

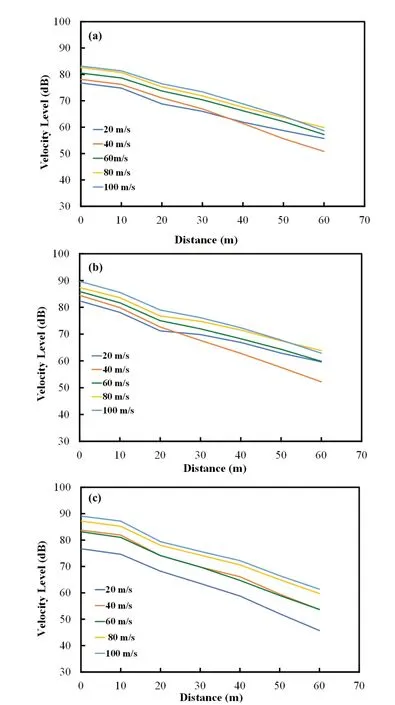
Fig.8 Variation of velocity attenuation at different train speed for different cases: (a) nominal model Model 1; (b) when reduction in depth of tunnel Model 2; (c) when reduction in elastic modulus of soil layers Model 3

4.2 Vertical acceleration

Vertical acceleration at the middle of the ground surface for three different models has been compared.For the nominal model (Model 1) (Table 2), a maximum of 11.97 mm/s2vertical acceleration has been observed at 100 m/s of train speed (Fig.9(a)) but this effect becomes magnified as 24.7 mm/s2.This is because when the tunnel depth is reduced to 6 m, the frequency of vibration increases, and the waves travel faster with sufficient energy associated with them (Fig.9(b)).Further, the reduction of the soil layer modulus (E1=1.5 MPa,E2= 5 MPa), i.e., in Model 3, also affects the vertical acceleration.It increased up to 17.11 mm/s2for 100 m/s of train speed, since the waves travelling in the soft soil had greater amplitude to carry the same energy.However, with the damping properties of the soil, the energy was absorbed in soft soil and its effects decayed with time, whereas the frequency decreased when compared to Model 1 (Fig.9(c)).Hence, a metro tunnel at shallow depth and in soft soil drastically affected the vertical acceleration.Accordingly, more caution should be given to design new structures or existing structures that are located near shallow metro tunnels with prevailing soft soil conditions nearby.

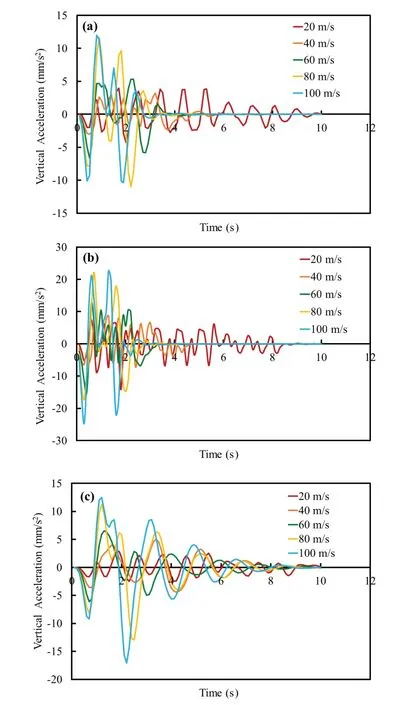
Fig.9 Comparison of the vertical acceleration at the middle of ground surface for (a) Model 1; (b) Model 2; (c) Model 3

4.3 Horizontal acceleration

The effect of the train speeds on three numerical models, i.e., Model 1, Mode 2 and Model 3, on two zones, i.e., on the ground surface that contains the structure (shown by the left arrow) and the ground area without a structure, i.e., the free surface (shown by right arrow) are shown in Fig.6.

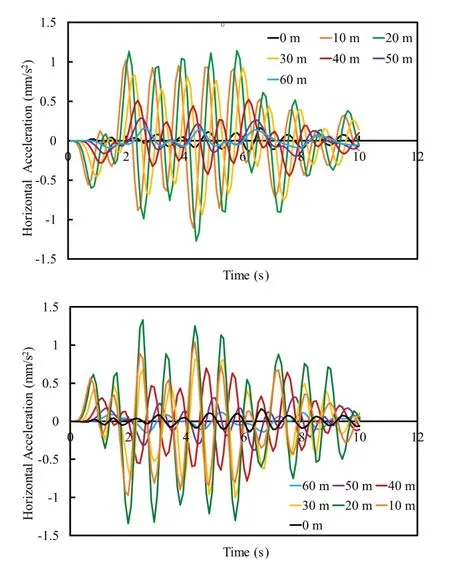
Fig.10 Case 1: Model 1 horizontal acceleration at middle cross-section of ground surface at 20 m/s (a) right side without structure, (b) left side with structure

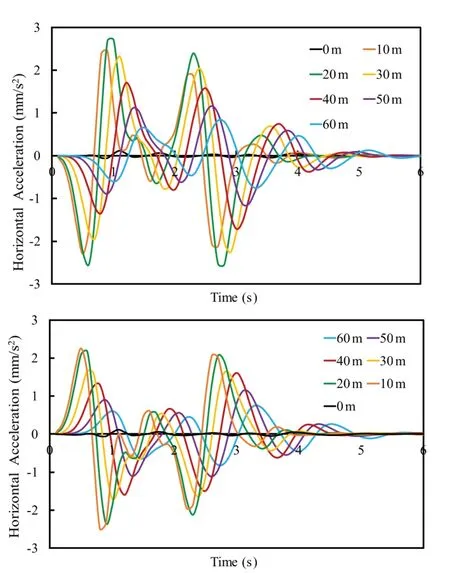
Fig.11 Case 1: Model 1 horizontal acceleration at middle of ground surface at 60 m/s (c) right side without structure,(d) left side with structure

The effect of vibrations has been observed with the help of horizontal acceleration at these two zones,as the vertical acceleration was counterbalanced by the weight of the structure and horizontal acceleration and its amplification was more adversely affect the structure(see Fig.10, Fig.11 and Fig.12).

The effect of train speed at different locations from the right of the center of the ground surface (without any structure) and from the left of the center of the ground surface (with structure) is represented in Figs.10(a), 10(b)for 20 m/s, Figs.11(c), 11(d) for 60 m/s, and Figs.12(e),12(f) for 100 m/s.

The horizontal acceleration was observed more on the left side of center (i.e., with structure) at low train speeds but this effect was reversed at higher train speeds.The effect of the horizontal acceleration was more predominant at a distance of 10 m to 40 m from the center, where at lower speeds, the time period for wave response was primarily due to its low frequency, which was one of the reasons it affected the nearby structure.Therefore, higher structures/skyscrapers which are to be constructed near high-speed metro tunnels in the range of 40 m should be designed and analyzed with proper consideration of vibrational effects.This effect should be reversed for the reduction in overburden pressure and for reduction of the elastic modulus for soil layers.

4.4 Effect of change in overburden pressure

Horizontal acceleration was observed more on the right side of center (i.e., without structure) at low train speeds, but the effect was reversed at higher train speeds, i.e., more horizontal acceleration was observed at the left of the center of the ground surface at higher train speeds as shown in Figs.13, 14 and 15.This trend of horizontal acceleration was the reverse from that in nominal model (Model 1).The horizontal acceleration was more predominant at a distance of 10 m to 40 m from the center.Hence, high structures which are close to the metro tunnels and are in the range of 10 m to 40 m should be provided with proper ground improvement techniques, if the acceleration value reaches beyond consideration at the time of design.

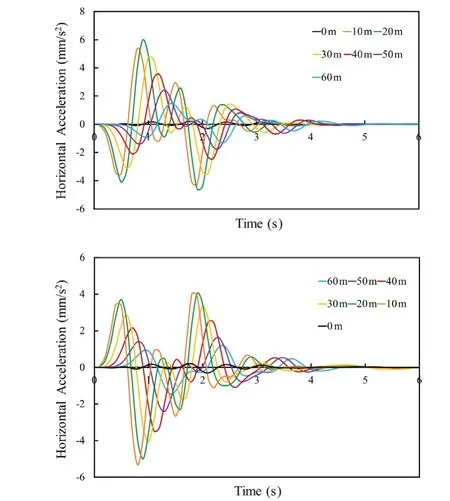
Fig.12 Case 1: Model 1 horizontal acceleration at middle of ground surface at 100 m/s (e) right side without structure,(f) left side with structure

4.5 Effect of elastic modulus of soil layers

Fig.13 Case 2: Model 2 horizontal acceleration at middle cross-section of ground surface at 20 m/s (a) right side without structure, (b) left side with structure

Fig.14Case 2: Model 2 horizontal acceleration at middle cross-section of ground surface at 60 m/s (c) right side without structure, (d) left side with structure

The pattern or variation of horizontal acceleration was observed to be same as that of the nominal model;i.e., at low velocity vibrational effects were more on the left side (with structure) but had higher values for the condition where the elastic modulus of the soil layers have been reduced.As the stiffness of soil reduced, the amplification occured in the acceleration values, but on the other hand, the vibrational effect also dampened at a faster rate (see Figs.16, 17 and 18).

4.6 Effect on pile raft

Three points, two on the extreme left and right and one on the middle at the edge of the raft shown as Points A, C and B, respectively, (see Fig.3) were selected to observe the results.Greater differential settlement and

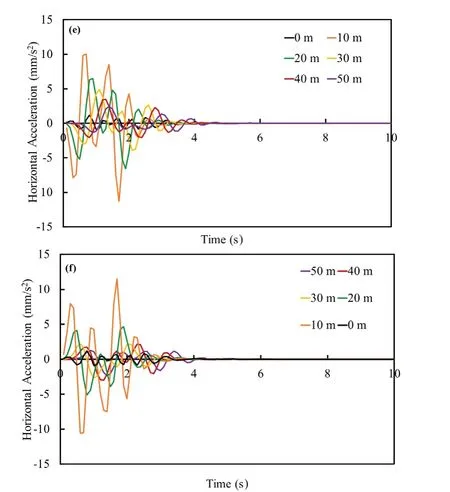
Fig.15 Case 2: Model 2 horizontal acceleration at middle cross-section of ground surface at 100 m/s (e) right side without structure, (f) left side with structure

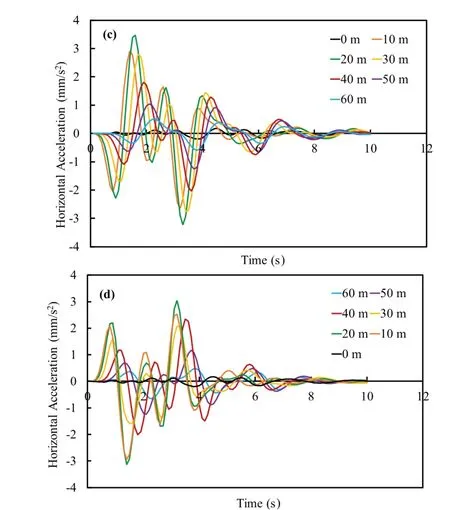
Fig.17 Case 3: variation of soil modulus (E1, E2) (Model 3)effect on horizontal acceleration at speed 60 m/s(c) without structure, (d) with structure

Fig.18 Case 3: variation of soil modulus (E1, E2) (Model 3)effect on horizontal acceleration at speed 100 m/s(e) without structure, (f) with structure

Fig.16 Case3: variationofsoilmodulus (E1,E2)(Model3)effecton horizontalacceleration atspeed20 m/s(a) without structure, (b) with structure the heaving effect was observed at higher train speeds.For the nominal model (Model 1), the max differential settlement observed was 0.123 mm for the 80 m/s train speed, while the max differential settlement observed was 0.136 mm and 0.671 mm for the 100 m/s train speed for Model 2 and Model 3, respectively.The tension zone was also observed at a later time period.Differential settlement was calculated (see Figs.19, 20 and 21) by subtracting the peak values of the higher and lower value curves of the two extremes points on the raft.

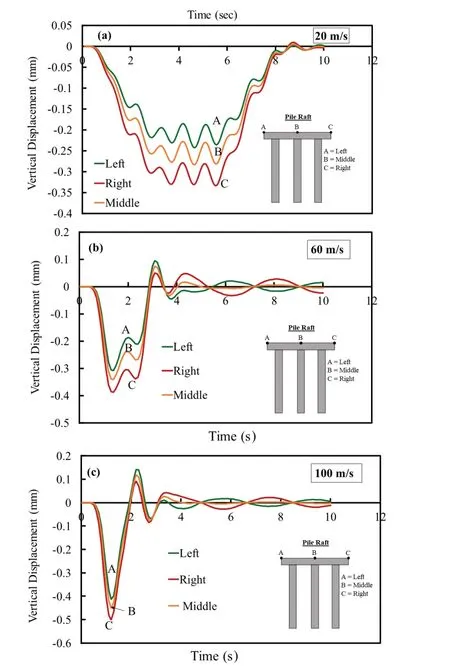
Fig.19 Effect on vertical displacement at left, middle and right point on raft at (a) 20 m/s, (b) 60 m/s, (c) 100 m/s for Model 1

Fig.20 Effect on vertical displacement at left, middle and right point on raft at (a) 20 m/s, (b) 60 m/s, (c) 100 m/s for Model 2

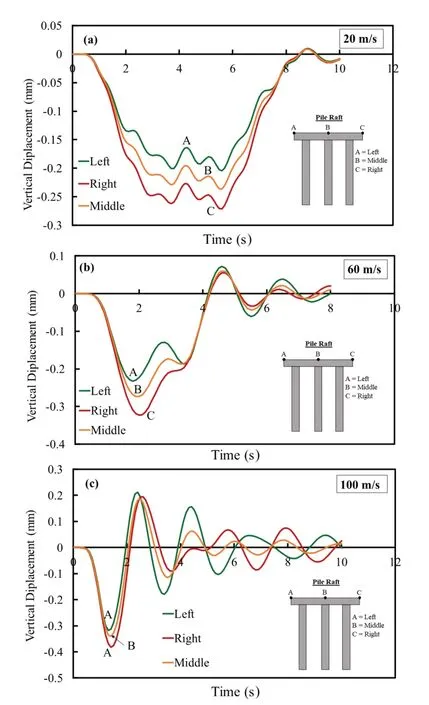
Fig.21 Effect on vertical displacement at left, middle and right point on raft at (a) 20 m/s, (b) 60 m/s, (c) 100 m/s for Model 3

Displacement contours for various speeds and for various models were also observed.Displacement contours were generated for the vertical displacement in the globalZ- direction.A comparison of displacement contours were observed (see Figs.22, 23 and 24) where the maximum displacement represents the downward settlement and the minimum displacement represents the heaving.

4.7 Displacement contours

From Figs.21, 22 and 23, the images in the left column represent the heaving and those in the right column represent the downward settlement.Figure 22 shows the response for all three models for the speed of 20 m/s.Similarly, Figs.23 and 24 show the response for 60 m/s and 100 m/s, respectively.

It was seen that by lowering the stiffness, the affected zone area also increased and by lowering the tunnel depth, the affected zone was shifted towards the structure.Figures 21, 22 and 23 illustrate the effect on the ground and the surface structure at different train speeds.

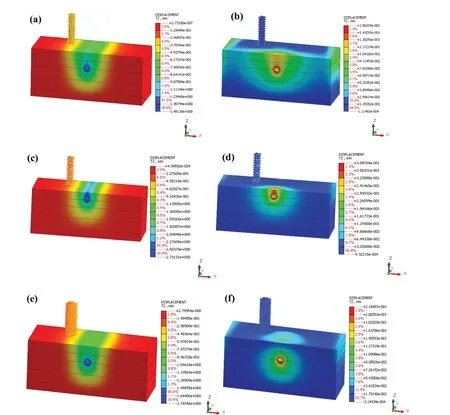
Fig.22 Left column ((a), (c), (e)) min displacement; right column ((b), (d), (f)) max displacement at 20 m/s.(a), (b) Nominal model;(c), (d) for reduction in overburden pressure; and (e), (f) for reduction in elastic modulus

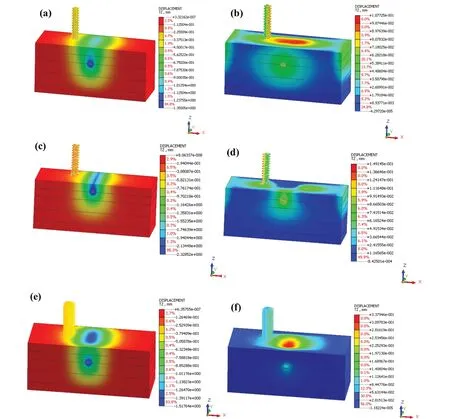
Fig.23 Left column ((a), (c), (e)) min displacement; right column ((b), (d), (f)) max displacement at 60 m/s.(a), (b) Nominal model;(c), (d) for reduction in overburden pressure; and (e), (f) for reduction in elastic modulus

5 Conclusions

This study concentrates on the simulation of moving train dynamic load, measurement of ground surface vibrations and their effects on nearby structures.It was performed by using finite element based numerical analysis.The results were recorded on the middle horizontal cross-section of the model.The conclusions given below are valid for the conditions assumed in the analysis.

(1) The maximum velocity level at the mid-point was found for different cases at levels sufficient to cause human annoyance.Velocity levels of 83.1 dB, 88 dB and 89.09 dB were found in Model 1, Model 2 and Model 3, respectively.Hence, a decrease in the overburden pressure and a reduction in the strength of the soil media increases the annoyance level.However, as the distance from center increases, these values were reduced.The limit of the velocity level was also confirmed to be within the guidelines of the Federal Transit Administration and Indian standard noise pollution.

(2) It was observed that reduction in overburden pressure affects the vertical acceleration and vertical velocity at the center; i.e., if the tunnels are to be constructed at shallow depth with less stiffsoil, then the effects of vibration will be larger in magnitude.This may be due to lack of cushioning effect, provided by the thick soil cover which can absorb vibrations and distribute it uniformly thereby avoiding any collateral damage.

(3) It was found that the effect of horizontal acceleration was magnified in the periphery of 10 m to 40 m distance from the point of load application.This could be due to attenuation of waves and their superimposition, thereby increasing the magnitude of deformations manifolds.Hence, horizontal acceleration and its effects should be considered when constructing any new structure in this zone and proper ground improvement techniques should be applied to the existing structures.The tunnel was analyzed at shallow depth with existing nearby structures; it was also observed that at higher velocity, the horizontal acceleration increased.Hence, the train induced vibrational analysis becomes more important in preventing the failure of existing structures and the design of new structures.

(4) In the analysis, heaving was not observed at lower train speeds in the raft foundation, but as the speed increased, the heaving effect and the differential settlement also increased.Heaving occured mainly due to accumulation of the energy at a point due to higher train speed.As soon as the train passed through the tunnel, a large number of vibrations were dissipated across and along the structure.Soil structure interaction played an important role.At higher train speeds, the induced vibrations were accumulated in a very small span of time.However, with lower train speeds, differential settlement and heaving decreased.

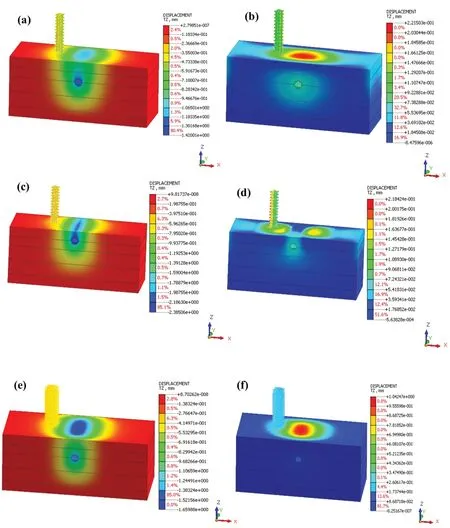
Fig.24 Left column ((a), (c), (e)) min displacement right column ((b), (d), (f)) max displacement at 100 m/s.(a), (b) Nominal model;(c), (d) for reduction in overburden pressure; and (e), (f) for reduction in elastic modulus

(5) This study will assist in the design of underground as well as ground structures.The effect of moving train vibrations needs to be considered while designing new structures, since for nearby tunnels, even a minute amount of differential settlement can lead to great devastation.The effect of moving train vibrations should also be analyzed to provide suitable ground improvement techniques to reduce the vibrational effects on existing structures near the tunnels and to provide safety for nearby inhabitants.