Reliability-based life-cycle cost seismic design optimization of coastal bridge piers with nonuniform corrosion using different materials

Wu Xiangtong, Yuan Wenting and Guo Anxin

1.Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters of the Ministry of Industry and Information Technology, Harbin Institute of Technology, Harbin 150090, China

2. Key Lab of Structures Dynamic Behavior and Control of the Ministry of Education, Harbin Institute of Technology,Harbin 150090, China

3.Institute of Transportation, Inner Mongolia University, Hohhot 010070, China

Abstract: Reinforcement corrosion is the main cause of performance deterioration of reinforced concrete (RC) structures.Limited research has been performed to investigate the life-cycle cost (LCC) of coastal bridge piers with nonuniform corrosion using different materials.In this study, a reliability-based design optimization (RBDO) procedure is improved for the design of coastal bridge piers using six groups of commonly used materials, i.e., normal performance concrete (NPC) with black steel (BS) rebar, high strength steel (HSS) rebar, epoxy coated (EC) rebar, and stainless steel (SS) rebar (named NPC-BS,NPC-HSS, NPC-EC, and NPC-SS, respectively), NPC with BS with silane soakage on the pier surface (named NPC-Silane),and high-performance concrete (HPC) with BS rebar (named HPC-BS).First, the RBDO procedure is improved for the design optimization of coastal bridge piers, and a bridge is selected to illustrate the procedure.Then, reliability analysis of the pier designed with each group of materials is carried out to obtain the time-dependent reliability in terms of the ultimate and serviceability performances.Next, the repair time of the pier is predicted based on the time-dependent reliability indices.Finally, the time-dependent LCCs for the pier are obtained for the selection of the optimal design.

Keywords: reliability-based design optimization (RBDO); life-cycle cost (LCC); nonuniform corrosion; coastal bridge pier; repair

1 Introduction

Chloride-induced corrosion of reinforcements is a major causes of deterioration of reinforced concrete (RC)structures (Otienoet al., 2019; Val, 2007); this effect has been widely recognized and may cause significant consequences (Limet al., 2016).It is reported that in 2002, the annual direct cost of RC bridge corrosion was more than $8.3 billion in the United States, and almost 15% of the bridges were structurally deficient due to reinforcement corrosion (Kochet al., 2002),which was mainly caused by the use of deicing salt and the marine environment.For coastal bridges, corrosion is serious and widespread due to exposure to severe corrosive environments.The chloride from external environments penetrate to the surface of steel embedded in the RC structures, and corrosion starts immediately when the chloride ion concentration reaches the chloride threshold concentration.Due to the expansion property of corrosion products, cracks and spalling (Shekharet al., 2018; Vidalet al., 2004) will occur on the surface of the concrete cover with the accumulation of corrosion products, which will lower the serviceability performance of the structures.Moreover, corrosion will reduce the cross-sectional area of the reinforcement(Apostolopouloset al., 2013) and the bond strength between the reinforcement and the surrounding concrete(Coronelliet al., 2012; Zhanget al., 2017).Thus, the load-bearing capacity of the structures will be weakened,and the failure pattern may change from ductile failure to brittle failure (Maet al., 2012).

Maintenance or repair activities need to be conducted when the performance of the structure reaches the limit states.Patching and overlay are commonly used methods for the repair of chloride-contaminated RC structures.Patching is used to replace small areas of deteriorated (i.e., cracked and spalled) concrete and clean the contaminated reinforcement, while overlay is used to replace the contaminated concrete and reinforcement to restore the structure to the original quality (Sohanghpurwala, 2006).Corrosion resistant materials, such as stainless steel (SS) rebar and highperformance concrete (HPC), are more expensive than ordinary materials, such as black steel (BS) rebar and normal performance concrete (NPC).However, due to the high critical chloride threshold (Clth) of SS and the low permeability of HPC, less frequent maintenance and repair activities are required for structures using these corrosion-resistant materials; thus, tremendous maintenance costs will be saved during the service life of the structures.In addition, due to the high yield strength of high strength steel (HSS), its application will reduce the amount of reinforcement required and carbon dioxide emissions, which may lead to a lower investment, although the price of HSS is higher than that of BS.Therefore, to compare the cost-effectiveness of using different design materials for a specified coastal bridge pier in the long run, the life-cycle cost (LCC)should be evaluated.

Past and current studies in the literature regarding theLCCof RC structures exposed to corrosive environments can be divided into two categories: one uses a deterministic-based method, and the other uses a reliability-based method (Sajedi and Huang, 2019).The main objective of deterministic-basedLCCresearch is to select the cost-effective design materials of structures without considering the randomness of parameters.For instance, Labi and Cope (2009) estimated theLCCof a bridge deck using SS and BS considering corrosion effects.The results showed that the use of SS significantly reduced theLCC, although it led to a higher initial construction cost (Cinitial).Daigle and Lounis (2006) compared the cost-effectiveness of using HPCs containing different supplementary cementitious materials to that of NPC for an RC bridge deck.These authors concluded that, in the long run, agency costs,user costs, and environmental impacts of the HPC deck were more cost-effective than those of the NPC deck.The main shortcoming of the deterministic-based method is that the variability of the parameters is not considered in the design process, which may lead to imprecise results.

The core of the reliability-basedLCCmethod is optimization, which simultaneously minimizes the cost and maximizes the reliability of the structures considering the variability of the key parameters relevant in the design process.Val (2007) investigated the influence of the uncertainties of corrosion parameters on theLCCof RC structures.Sajediet al.(2016) proposed a reliabilitybased multi-objective design optimization procedure for RC structures exposed to corrosion.The procedure uses a nondominated sorting genetic algorithm (GA) to maximize the reliability of the structures and minimize the associated material costs.These researchers illustrated the procedure for an interior T-beam with three types of materials, namely, normal strength concrete (NSC) with BS rebar (named NSC-BS), NSC with epoxy coated (EC) rebar (named NSC-EC), and HPC with BS rebar (named HPC-BS), considering the prevailing variables of the parameters.They concluded that, for a service life of 100 years, HPC-BS is the recommended material for the studied beam.Recently,Sajedi and Huang (2019) developed a reliability-based design optimization (RBDO) procedure to quantitatively compare theLCCof different design and repair materials.The procedure adopts the GA technique for optimization.As an illustration, six groups of materials were used for the design of an interior T-beam affected by deicing salt using the proposed procedure, andCinitialwas taken as the optimization objective.Then, the time-to-repair was predicted, and theLCCwas calculated.The main drawback of these studies is thatLCCis not taken as the optimization objective.On the other hand, the abovementioned studies mainly focus on RC bridge decks, and very few studies have been reported regarding the design optimization of coastal RC bridge piers.

To achieve an optimal design, it is extremely important to utilizeLCCas the optimization objective,that is, to include the recurrent expenditure after the construction of the structures.Using this approach,more accurate and reliable optimization results can be obtained.The RC bridge pier is the main component that supports the upper structures, and its corrosion is the most serious in coastal bridges.The coastal bridge pier is usually divided into three zones from top to bottom along its height according to the corrosion risk, i.e., the atmospheric zone, splash and tidal zone, and submerged zone.Usually, due to the wet-dry cycle, the corrosion in the splash and tidal zone is the most serious, followed by the atmospheric zone because of the simultaneous presence of chloride ions and humidity in the air, while the corrosion in the submerged zone can be negligible due to the lack of oxygen.Considering the complexity of the marine environment, nonuniform corrosion along the height of the pier should be taken into account when evaluating the corrosion degree of the piers.

The purpose of this study is to compare the costeffectiveness of six groups of commonly used materials for the design optimization of a coastal bridge pier and the difference in the design results between different optimization objectives.These six groups of materials are NPC with BS rebar, HSS rebars, EC rebar, and SS rebar (named NPC-BS, NPC-HSS, NPC-EC, and NPCSS, respectively), NPC with BS with silane soakage on the pier surface (named NPC-Silane), and HPC containing 30% fly ash as a replacement of cement in mass with BS (named HPC-BS).First, an RBDO procedure is improved, and a bridge pier is selected to conduct the procedure by minimizing the cost, given the corresponding constraints, in whichCinitialandLCCare taken as the optimization objectives in the design procedure to compare the difference in the design results.Then, reliability analysis of the pier designed with each group of materials is carried out to obtain the time-dependent reliability in terms of the ultimate and serviceability performance.Next, the repair time of the pier is predicted based on the time-dependent reliability indices.Finally, the time-dependentLCCs for both the pier withCinitialandLCCas optimization objectives are obtained to select the optimal design materials for the coastal bridge pier.It is hoped that this research will contribute to a deeper understanding of the design optimization of coastal RC bridge piers exposed to nonuniform corrosion.

2 Corrosion modeling in RC structures

The corrosion process of RC structures can be divided into three phases: the diffusion phase, the rust accumulation phase and the crack propagation phase(Suwito and Xi, 2004).However, it is difficult to describe the rust accumulation phase and the crack propagation phase since the corrosion rate of these two phases are influenced by various factors, such as the water-cement ratio of the concrete, humidity, chloride ion concentration,and pitting corrosion.To simplify the aforementioned problems and facilitate the modelling of corrosion for RC structures, some scholars divided the corrosion process into two phases: corrosion initiation phase and corrosion propagation phase with a constant corrosion rate (Sajedi and Huang, 2019; Tuutti, 1982).The assumption of two-phase corrosion is also adopted in this study in the numerical model of the deteriorated RC bridge piers.In the corrosion initiation phase, chloride ions from the external environment diffuse through the concrete cover to the surface of the reinforcement and accumulate until the chloride ion concentration reachesClth.For the reinforcements adopted in this research, the critical chloride thresholdsClth,BS,Clth,HSS,Clth,EC, andClth,SSof BS, HSS, EC, and SS are 1, 1, 4.6, and 16.7 kg/m3,respectively (O’Reillyet al., 2011; Sajedi and Huang,2019; Weyerset al., 1993).The above values ofClth,BS,Clth,EC, andClth,SSare used for RC bridge component(such as bridge decks), those values are also appropriate for the bridge piers.Then, the passive film is destroyed,and corrosion is initiated.After the corrosion initiation phase, the corrosion propagation phase starts, during which the cross-sectional area and mechanical properties of the reinforcement will be decreased.For the expansion property of the corrosion products, cracks and spalling will appear on the surface of the concrete cover, and the bond strength between the concrete cover and reinforcing steel bars will be decreased.In this study, an adequate development length of steel bars is assumed; thus, the influence of the reduction of the bond effect can be neglected.The quantitative calculation of these two corrosion degradation phases in RC structures is illustrated below.

2.1 Corrosion initiation phase

Due to the complexity of obtaining the time-varying chloride concentration on the bridge pier surface and the inhomogeneity of concrete materials, the chloride ion concentration on the pier surface and diffusion coefficient are assumed to be constant.The initial chloride concentration in the concrete is assumed to be zero.Based on the solution of Fick’s second law, the chloride ion concentration at a distancexfrom the nearest concrete surface at timet,C(x,t), can be calculated as follows (Alipouret al., 2013, Sohanghpurwala, 2006;Tuutti, 1982):

whereCsis the chloride ion concentration on the pier surface (kg/m3); erf()· is the Gaussian error function;andDcis the diffusion coefficient of chloride ions in concrete (cm2/s).Dcis influenced by many factors, such as the type of cementitious materials, water-binder ratio,and concrete quality.According to the previous research(Val and Stewart, 2003), theCsvalues in the atmospheric zone and splash and tidal zone are taken as 2.95 and 7.35 kg/m3, respectively.To simplify the calculation procedure, the chloride ion diffusion coefficient is assumed to be constant, i.e., 2×10-8for NPC (Vu and Stewart, 2000) and 0.3595×10-8cm2/s (Lenget al., 2000)for HPC with 30% fly ash in mass used as a replacement for cement.

As previously mentioned, corrosion is initiated when the chloride concentration on the surface of the steel rebar reachesClth.Thus, the corrosion initiation time of the reinforcementtincan be determined by settingx=Cb, in whichCbis the nearest distance between the rebar and the concrete surface (mm), andC(Cb,t) =Clthin Eq.(1).Then,tincan be obtained by solving Eq.(1),which is derived as Eq.(2).Due to the difference between the longitudinal reinforcement and stirrups in terms of the thickness of concrete over them, the value ofCbin Eq.(2), equals the concrete coverCfor stirrups,andCplus the stirrup diameterdst, for longitudinal reinforcement.

2.2 Corrosion propagation phase

The direct effects of corrosion propagation on RC structures include a reduction in the cross-sectional area and yield strength of the steel rebar and cracks on the concrete cover.These effects will diminish the bearing capacity and accelerate the degradation of the structures and are generally considered to be the time-dependent reinforcement diameter,d(t), time-dependent yield strength,fy(t), and time-dependent concrete surface crack width,wcr(t), which can be calculated as (Duet al., 2005; Sajedi and Huang, 2019; Webster and Clark, 2000):

whereQ(t) is the percentage mass loss of the reinforcement at timet;d0is the initial diameter of the reinforcement;fy0is the yield strength of the uncorroded reinforcement;αdis the volumetric expansion ratio of the corrosion products to the intact steel, generally assumed to be 2 (Shekharet al., 2018);tcris the first cracking time of the concrete cover, equal totinplus the duration from the beginning of corrosion to the first cracking,tcr0;xcris the reinforcement radius loss corresponding to initial corrosion-induced cracking (μm); andicorris the corrosion current density.According to the study of Rodriguez and Andrade (2001), the corrosion current densities in the atmospheric zone and splash and tidal zone are 0.5-5 μA/cm2and 1-10 μA/cm2, respectively.Within this parameter range, based on the previous research (Yuanet al., 2017), the average corrosion current density is assumed to be 3 μA/cm2and 6 μA/cm2for the atmospheric zone and splash and tidal zone,respectively.

3 Reliability-based design optimization procedure

Different materials may lead to different initial costs and maintenance costs.For example, the price of HPC is higher than that of NPC; SS, HSS and EC are more expensive than BS; and silane soakage treatment will also increaseCinitial.However, HPC has a smaller permeability than NPC, which can slow the diffusion process of chloride ions.SS, EC, and silane soakage are more corrosion resistant than BS.HSS has a higher yield strength than BS; thus, steel can be saved, and the construction costs can be reduced.These materials can delay the corrosion initiation time and reduce maintenance costs or construction costs.Optimization minimizes the cost of the structures while ensuring the performance requirements, and it is an effective way to select the optimal design material and maintenance strategies for RC structures exposed to corrosive environments.Sajedi and Huang (2019) proposed a single objective optimization procedure for RBDO under probabilistic and deterministic constraints and used it for the design optimization of an RC bridge interior T-beam exposed to deicing salt using different design materials.The proposed procedure is shown as follows:

whereyis the design parameter (e.g., bridge pier diameter,cover thickness, and amount of reinforcing bars);xis the input random variable (e.g., concrete compressive strength and steel yield strength); ˆyis the mean value ofy;βi(x,y) is theith reliability index;βTDiis the threshold value of theith reliability index for the design of the pier which is defined by the design code (e.g., the Chinese standard for reliability design (GB/T 50283-1999,1999) recommends a target reliability index of 4.2 for ductile components of highway bridge structures with secondary security level);Djis thejth deterministic constraint provided by the design codes (for example,the reinforcement ratio, the axial compressive ratio, and the horizontal displacement limit under E2 earthquake motion);Dmin,jandDmax,jare the minimum and maximum value ofDj, respectively;ykis thekth design parameter;andandare the lower and upper limit ofyk,respectively.

The GA techniques can be adopted to obtain an optimal design.The GA is effective at solving nonlinear problems, especially for the optimization of multiobjective problems, and has been widely applied to complex optimization problems (Denget al., 2017;Holland, 1992).In this study, the global search algorithm is applied to the design optimization.

The probabilistic constraint in Eq.(9) ensures the capacity and serviceability performance.The reliability indexβi(x,y) can be calculated by the first-order reliability method (FORM) on the basis of Eq.(10) (Afshariet al.,2022; Chenget al., 2008; Ghasemi and Nowak, 2017), in whichgi(x,t) is the performance measure, known as the limit state function for theith limit state (e.g., ultimate limit state and serviceability limit state).For example, in a simply supported beam,xcan be a vector of the beam’s span and load.And an increased span or load increases the failure probability (Chenget al., 2008).Next, sett=0 to calculate the reliability indices of the intact structure.Other methods, such as Monte Carlo simulation, which can obtain the failure probability of the corresponding limit state, can also be adopted to calculate the reliability index.However, a major drawback of Monte Carlo simulation is the huge amount of calculation work.

A brief flowchart of the proposed optimization design procedure is shown in Fig.1.The constraints such as the probabilistic constraint, the deterministic constraint, and the ranges of design parameters are used to test the design parameters.For example,βiandDjcan be obtained based on the design parameters.If the constraints are not met, the design parameters must be changed and recalculated until the constraints are met,and then the cost has to be calculated.In addition,yis the vector of design parameters and is selected from the range given in the optimization design program so that the constraints are automatically satisfied.In addition,minimizing cost is the optimization objective; in other words, finding the minimum cost under the constraints.The optimization design procedure is achieved by the self-written program, as shown in Fig.1.Thus, the optimal design parameters can be obtained until the cost is the lowest.

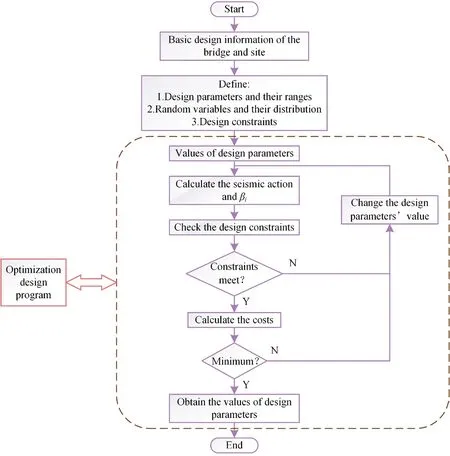
Fig.1 Proposed optimization design procedure

4 Seismic horizontal force calculation and deformation checking of the pier

Two-level fortification and two-stage design of bridges have been adopted in the code for the seismic design of bridges, namely, checking the strength of the bridges under slight earthquake action and checking the displacement of the bridge piers under great earthquake action.In this study, the seismic calculation of bridges is based on the seismic design code of China (JTG/T B02-01-2008, 2008), in which slight and great earthquake actions are named earthquake actions E1 and E2,respectively.Only the major parts of the calculation of seismic effects are illustrated below (see the “Guidelines for Seismic Design of Highway Bridges,” JTG/T B02-01-2008 (2008) for more details).

4.1 Seismic force calculation

The purpose of the first stage of bridge seismic design is to ensure the strength of the pier under a slight earthquake.Thus, the main goal is to obtain the seismic force demand on the pier.For regular bridges under earthquake action E1, the response spectrum method can be used to analyze the elastic seismic force.Simply supported bridges can be simplified to single-degreeof-freedom (SDOF) systems because the weight of the superstructure and cap beam is greater than that of the pier.The acceleration spectrum is expressed as

whereSmaxis the maximum value of the spectrum;Tis the natural period of the bridge;Tgis the characteristic period of the site;CE,iis the seismic significance coefficient;CE,sis the site coefficient;Cdis the damping modification coefficient; andAis the peak value of the basic ground acceleration in the horizontal direction.

Then, the horizontal seismic force acting on the top of the bearings can be calculated by

whereSh1is the value of the acceleration spectrum;Ctis the equivalent particle gravity at the top of the bearings;and g is the acceleration of gravity.The total maximum design seismic force,FE, requires a combination of the forces from the two horizontal directions.

4.2 Displacement demand and allowable displacement calculation

The objective of the second stage of bridge seismic design is to ensure that the displacement of the pier under a large earthquake is within the allowable displacement.Thus, the main goal is to determine the displacement demand of the pier under earthquake motion E2 and the allowable displacement of the pier.

The bridge pier enters the inelastic range under earthquake motion E2.According to the equal displacement rule (JTG/T B02-01-2008, 2008; Chopraet al., 2004; Vamvatsikos and Cornell, 2002; Veletsos and Newmark, 1960), the inelastic displacement is approximately equal to the displacement of the corresponding elastic model.Thus, the main objective is to calculate the displacement of the corresponding elastic model.When calculating the displacement of the elastic model, the section stiffness should be replaced by the effective section stiffness, which can be calculated as

whereEcis the elastic modulus of the pier;Ieffis the effective moment of inertia of the pier section; andMyandφyare the yield moment and equivalent yield curvature, respectively, which can be obtained through elastic sectional axial force-moment-curvature analysis.Then, the seismic force can be calculated by the response spectrum method, in whichCiequals that of earthquake motion E2.The displacement at the top of the pier in one horizontal direction can be obtained through the seismic force and the stiffness of the pier.

The allowable displacement,Δu, of the pier is given as

whereHis the height is the pier;Lpis the length of the equivalent plastic hinge;θuis the maximum allowable rotation of the plastic hinge;φuis the curvature of the ultimate state of the pier section; andKis the ductility safety factor and equals 2.

5 Life-cycle cost analysis (LCCA)

TheLCCof RC bridge piers exposed to coastal corrosive environments includesCinitial, the maintenance costs, and the failure costs (Frangopolet al., 1997).The failure costs are affected by many social factors and are difficult to consider.It is assumed for simplicity that the reliabilities of bridge piers using different design materials can be kept at the same level through design and maintenance.On the other hand, the main purpose of this study is to compare the relative costs of bridge piers using different materials and maintenance strategies.Thus, this assumption does not affect the qualitative nature of the final results.TheLCCpresented by the present value cost (PVC) can be calculated as

where the second term is the maintenance costs in whichCiis the expense at timei(years), which involves the costs of routine inspection, nondestructive evaluation, repair and overlay (Sajedi and Huang, 2019; Sohanghpurwala,2006) during the design service lifeof the structure,T;andris the discount rate, typically assumed to be 0.02(Kepleret al., 2000).

6 Case study

Sajedi and Huang (2019) applied the RBDO procedure to an interior T-beam of an RC bridge exposed to a deicing salt environment to compare the costeffectiveness of six groups of commonly used design materials.TakingCinitialas the optimization objective,these authors concluded that NSC-SS is the optimal design material for the selected T-beam.However,the expenditure after construction can significantly increase theLCCof the structure; thus, it is necessary to incorporate maintenance costs into the optimization process.In addition, bridge piers are significantly different from beams in terms of the form of the loads they are subjected to because piers bear not only the bending moment, which is caused by the horizontal force, such as the inertia force induced by earthquakes,but also the axial force.Furthermore, RC bridge piers in coastal environments may suffer more serious corrosion than bridge beams.In this study, a coastal bridge pier is selected to conduct the RBDO procedure to compare the cost-effectiveness of using six groups of materials.

The bridge pier in De Sortiset al.(1998) is adopted in this study.Figure 2 shows a schematic diagram of the bridge, including the dimensions of the pier.The height of the bridge pier is 14 m, and it is assumed that the heights of the submerged zone, splash and tidal zone,atmospheric zone, and bent cap are 2.1 m, 6 m, 3 m,and 2.9 m, respectively.The bridge span and diameter of the pier in the original bridge model are 50 m and 2.5 m, respectively.The dead load is 200 kN/m; thus, the concentrated load,F, is 10000 kN.According to the span of the bridge and the code, the design service life of this bridge is 100 years (JTG D60-2015, 2015).Assuming that the bridge in the area has a seismic fortification intensity of 8 degrees, the site category is Ⅱ, and the damping ratio is 0.05.Thus, according to the seismic design code of China (JTG/T B02-01-2008, 2008),Ais 0.2 g,Tgis 0.35 s, and theCE,ivalues for earthquake motion E1 and earthquake motion E2 are 0.43 and 1.3,respectively.

In this study, the following materials are used:concrete with a compressive strength offc= 43.05 MPa ,BS and EC with a yield strength offy= 377.54 MPa ,HSS with a yield strength offy,HSS= 676.2 MPa , and SS with a yield strength offy,SS= 563.5 MPa , and Young’s modulus of reinforcing steel,E, is assumed to be the same, i.e., 200 GPa.Assuming that the initial construction costs of the bent cap and the foundation for each group of materials are the same, no corrosion occurs during the design service life in these two zones.Thus, only the middle part of the pier, i.e., the part with the circular cross-section between the bent cap and the foundation, is considered in this study.

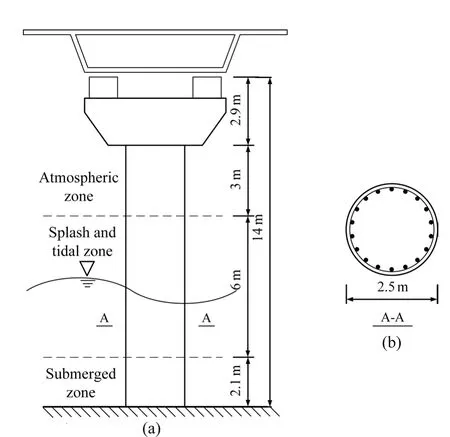
Fig.2 (a) Schematic diagram of the coastal bridge, and (b) cross section of the bridge pier

The bridge pier is redesigned in this study based on the RBDO procedure using six groups of materials: four groups of NPC with different reinforcements (i.e., NPCBS, NPC-HSS, NPC-EC, and NPC-SS), NPC with BS and silane soakage on the pier surface, and HPC with BS.The HPC used in this study contains 30% fly ash as a replacement for cement in mass corresponding to the chloride ion diffusion coefficient adopted in this study.The design variables in the pier are the pier diameter,D, concrete cover thickness,C, and total cross-sectional area of rebar,As.The stirrup spacing is 50 mm in the stirrup densification zone, which is assumed to be within 3 m from the bottom of the pier and 100 mm outside the stirrup densification zone.The diameters of the intact longitudinal rebardband stirrupdstare 32 mm and 16 mm,respectively.According to the seismic design code of China (JTG/T B02-01-2008, 2008), the reinforcement ratio of longitudinal rebar,ρ, should be in the range of 0.006 to 0.04; thus, the range ofAscan be calculated byDandρ, i.e.,As= πρD2/4.

7 Design optimization of the RC bridge pier using the RBDO procedure

Table 1 lists the variables used in the bridge pier design process, assuming thatD,As,s,db,dst, andFare deterministic variables and the other variables are random.The ranges of the design variables are given in Table 1, in which the range ofAsis determined byρandD.In particular, the range of values forDandCis based on practical applications.The mean values of the geometrical variables, strength variables, and load variable are as previously mentioned.Assuming that all random variables follow a normal distribution, the standard deviation (SD) forCis 10 mm.The coefficient of variation (CoV) of the yield strength of BS and the compressive strength of NPC are assumed to be 0.0685(GB/T 50283-1999, 1999), and 0.156 (Liet al., 2018),respectively.Additionally, it is assumed that theCoVof the compressive strength of HPC is equal to that of NPC and that theCoVs of the yield strength of EC,SS, and HSS are equal to that of BS.Thus, theSDs offy,fy,HSS,fy,SS, andfc,HPCcan be calculated, as shown in Table 1.Due to the large uncertainty of corrosion, theCoVof the corroded reinforcement is assumed to be 0.1.The horizontal earthquake load on the top of the pier is assumed to follow a normal distribution and has aCoVof 0.3.The unit price and critical chloride threshold value of the reinforcements, the unit price and diffusion coefficient of the concretes are listed in Table 2.Note that because the main purpose of this study is to select the optimal design materials for the bridge pier using the RBDO procedure and to compare the cost-effectiveness of the pier cost with different optimization objectives,a more appropriate distribution for the variables can be used.

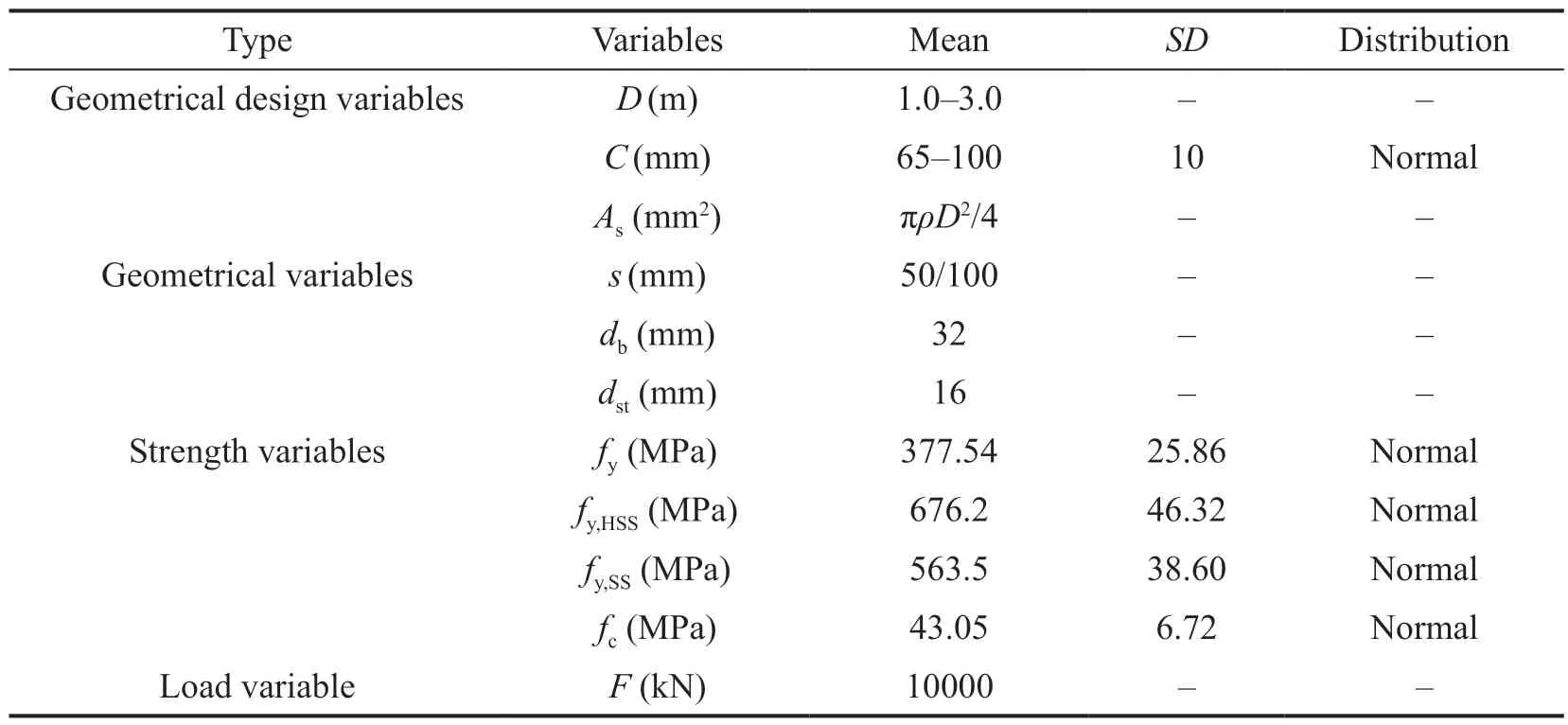
Table 1 Values of design variables

Due to the complexity of obtaining the bearing capacity of the bridge pier under axial and horizontal forces, in the RBDO procedure, the flexural failure mode of the bridge pier under constant axial force is regarded as the ultimate limit state for the design optimization.The bending capacity calculation of the RC bridge pier under constant axial force can be divided into two parts, i.e.,the capacities related to steel and concrete.The capacity related to reinforcement can be calculated using an integral operation by simplifying the longitudinal rebar to an equivalent steel ring, and the process is illustrated in detail as follows.Figure 3 shows the schematic diagrams for the calculation of the bending capacity, whereεyis the yield strain of the reinforcement and is equal to the yield strength divided byE;εcuis the ultimate compressive strain of concrete;Ris the radius of the bridge pier cross section;x0is the distance between the neutral axis and the edge of the tension side of the cross section;ris the radius of the equivalent steel ring;tis the thickness of the equivalent steel ring and is calculated byAsandr;θis the radian value in polar coordinates; andηand dAare the abscissa values and area of the differential element,respectively.To calculate the bending capacity of the section under constant axial force, the position of the neutral axis of the cross section needs to be determined.Because the axial compression ratio of the pier is less than approximately 0.1, the failure mode of the pier is close to flexural failure.Thus, it is assumed that the stress of the outermost longitudinal rebar on the tensile side just reaches the yield strength at the ultimate limit state.Based on the plane-section assumption and if the strain on the compression edge of the section reachesεcu, the critical position of the neutral axis,0x′, can be calculated as

whereC′ =C+dstis the distance between the longitudinal reinforcement and the pier cross-sectional edge.

Figure 3(a) shows the assumed strain distribution in the pier cross section.Then, the strainε(x) at positionxcan be calculated by Eq.(19), given the position of the neutral axisx0.The constitutive models of reinforcement rebar and concrete can be expressed as follows:

whereεis the strain of steel or concrete;is the concrete compressive strength; andε0andεcuare the peak and ultimate compressive strain of concrete, which are assumed to be 0.002 and 0.0033, respectively.Thus,the capacity of the cross section can be obtained based on the strain distribution and the constitutive models of reinforcement rebar and concrete.Figures 3(b) and 3(c) show the schematic diagrams for the calculation of the resultant forces of longitudinal reinforcement and concrete, respectively.In particular, in this study,the tensile strength of concrete is not considered in the calculation process due to its limited effect.In addition,as the core concrete is not in the three-dimensional compression state, the constraint effect of stirrups is not involved in the constitutive models for the core concrete.

For a given position of the neutral axis, the crosssectional bending moment and axial force can becalculated by integration based on the strain distribution and constitutive models of reinforcement and concrete given above, as expressed in the following equations

Table 2 Unit price and corrosion parameters of reinforcement and concrete

whereNsandNcare the axial forces related to the reinforcement rebar and concrete, respectively;MsandMcare the bending moments related to the longitudinal reinforcement and concrete, respectively; andNandMare the section axial force and moment, respectively.For the capacity calculation of the corroded pier,fyin the constitutive model of reinforcement should be replaced by the yield strength in Eq.(4).By adjusting the location of the neutral axis from0x′ to the compressive edge of the section, when the difference betweenNandFis smaller than 1% ofF, the correspondingMcan be regarded as the bending capacity of the pier, and the corresponding neutral axis is named the critical neutral axis.In this study, to improve the calculation efficiency, the bisection method is used to find the critical neutral axis.

The ultimate limit state function for the flexural failure mode can be expressed as

in which the variables can be expressed by random variables to calculate the reliability index as

whereM(t) is the bending capacity of the pier underF,which can be calculated by Eqs.(22)-(27);Wc=Mcfc′andWs=Msfsare the flexural moduli of the concrete and steel of the pier section, respectively;fc′andfsare the concrete compressive strength and steel yield strength, respectively;MEis the moment of the section caused by the horizontal earthquake force at the top of the pier;his the distance between the top of the pier cap and the pier section corresponding toME; and the meanings of the other variables are as mentioned above.For the case and random variables involved in this study,the reliability indexβifor the flexural failure mode of the pier under constant axial load can be calculated based on the limit state function.The corresponding limit state function ofβ1is Eq.(29), soβ1can be computed as follows:

For the calculation ofCinitialof the bridge pier, the transportation and installation costs are assumed to be included in the material costs.Thus,Cinitialin Eq.(17) can be calculated as follows:

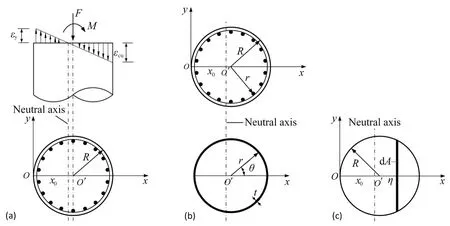
Fig.3 Schematic diagrams for bending capacity calculation: (a) strain distribution; (b) equivalent steel ring; and (c) concrete

To obtainLCCs, the costs of routine inspection and nondestructive evaluation and the expenditures of maintenance and repair due to reinforcement corrosion should be considered.The reliability index,β(t), as mentioned earlier, is used to evaluate the performance of the pier.Two limit state functions are used.One function is the ultimate limit state in terms of the flexural capacity of the pier under constant axial force,g1(x,t), as given in Eq.(28).The other is the serviceability limit state in terms of crack width,g2(x,t), which can be defined as follows:

wherewcr,limitis the serviceability capacity of the crack width andwcr(t) is the serviceability demand of the crack width caused by the expansion of the corrosion products, which can be determined by Eq.(5).Due to the complexity ofwcr(t) in calculating the crack width,the design checkpoint method (Zhang, 2009) is adopted to calculate the reliability indexβ2, taking into account the probability distribution of the random variables.Additionally, the calculation ofβ2is performed iteratively in the design optimization program.

For the variables used in the time-dependent reliability analysis,wcr,limithas a normal distribution with a mean value of 0.5 mm andSDof 0.1 mm (Sajedi and Huang, 2019); the other variables are given in Table 1.Assuming silane soakage on the bridge pier can provide a 10-year protection, i.e., within 10 years, the chloride ion concentration on the concrete surface beneath the soakage is 0 and immediately reaches the environment chloride ion concentration at the end of the 10th year.

In this study, the design service life is 100 years for the bridge pier.The reliability index,β(t), will decrease with time due to corrosion.Before corrosion initiation (t＜tin),the reliability index for the ultimate limit state,β1(t),equals the value of the intact pier.For the serviceability limit state, according to a previous study (fib, 2012), the target reliability index,βTD2, is recommended as 1.5.By settingt=0 in Eq.(32), the serviceability reliability index can be calculated asβ2=5 for all designed piers.Thus,both the reliability indices for the serviceability limit state and ultimate limit state satisfy the requirements.

As mentioned in Eq.(17), theLCCcontainsCinitialandCi, which involves the costs of routine inspections,nondestructive evaluation, repair and/or overlaying(Sajedi and Huang, 2019).It is assumed that the cost of routine inspection is ¥4/m2and an inspection is carried out every two years for all designed piers.The cost of nondestructive evaluation is assumed to be ¥80/m2starting at the 5th year, and this evaluation is carried out every 5 and 10 years for NPC and HPC piers, respectively.The time interval of nondestructive evaluation for HPC is longer than that for NPC because the permeability of HPC is lower than that of NPC,leading to a remarkable delay of the corrosion initiation phase.The repair activities of the pier are assumed to be conducted when eitherβ1orβ2reaches the specified threshold values ofβT1orβT2.In this study,βT1is assumed to be 3.7, andβT2is assumed to be 1.28 (Sajedi and Huang, 2019).Note that the degradation ofβ1andβ2is due to the corrosion of the longitudinal rebar and stirrups, respectively.Whenβ1reachesβT1orβ2reachesβT2, restoration measures are needed to maintain the performance of the pier.As mentioned above, patch repair and overlay are adopted for the restoration of the serviceability performance and ultimate performance with a cost of ¥400/m2and ¥1200/m2, respectively.Note that for patch repair, assuming that only 10% of the surface needs to be repaired, this repair only restoresβ2to the corrosion initiation state (i.e.,β2=5) and has no effect onβ1, while the overlay will restore not onlyβ1but alsoβ2to the value when the pier is just built (i.e., whent=0).Due to the difference in chloride ion concentration on the pier surface between the atmospheric zone and the splash and tidal zones, the corrosion initiation phase and corrosion propagation phase will be different between these two zones; thus, the patch repair and overlay of these two zones are considered separately in this study.It is also worth mentioning that no corrosion will occur on SS within the design service life due to its high corrosion resistance, and thus, except for the routine investigation,other maintenance actions are not required.

Based on the aforementioned corrosion parameters of the materials and environment and the calculation ofCinitialandCi, for a pier with given geometric parameters using the materials mentioned herein,CinitialandLCCcan be calculated.In this study,CinitialandLCCare taken as optimization objectives in the RBDO in Eq.(9) to compare their difference on the design results.Taking into account the features of the optimization case adopted in this research, such as the constraints considered,nonuniform corrosion and different optimization objectives, a more detailed and specific optimization design procedure is given, as shown in Fig.4.

The design parameters and the correspondingβ1,Cinitial, andLCCof the two optimization objectives for the six groups of materials obtained from the RBDO procedure are shown in Table 3.For the design optimization results withCinitialandLCCas optimization objectives (Group A and Group B, respectively), theCinitialvalues of the NPC-HSS pier based on the RBDO procedure is ¥37137 and ¥38407, respectively, which are the lowest among the six groups of materials.TheCinitialvalue of the NPC-BS pier for Group A and Group B are ¥82997 and ¥88694, respectively.As the effect of corrosion is not considered in the design process in Group A, theLCCof NPC-HSS is ¥84716, which is 2.28 times itsCinitialvalue and much higher than that in Group B.Because SS will not be corroded during the design service life, theCinitialandLCCof NPC-SS in Group A and Group B are the same.The results in Table 3 also indicate that the cover thickness in Group A is close to the lower-bound value, which is similar to the results of the optimal design of an RC bridge T-beam (Sajedi and Huang, 2019).However, the cover thickness of NPCBS and NPC-Silane piers in Group B equals the upperbound value, and the cover thickness of NPC-HSS is close to the upper-bound.This is not always the case, as the design results depend on the applied loads, the limits of geometric parameters, the properties of the materials and environment, and the price of the materials.

Based on the geometric parameters of the piers and the specified corrosion parameters, the time-dependent reliabilities,β1andβ2, can be obtained.As the cover thickness of the NPC-BS, NPC-HSS and NPC-Silane piers in Group B is greater than that of Group A, the corrosion of the piers in Group B is not as serious as that of Group A.Thus, only the time-dependent reliability of the piers in Group A is displayed, as shown in Fig.5,where the solid black line and dashed black line refer toβ1andβ2in the splash and tidal zone, respectively, the solid blue line and dashed blue line refer toβ1andβ2in the atmospheric zone, respectively, and the solid red line and dashed red line refer toβT1andβT2, respectively.The NPC-EC pier and NPC-SS pier are not corroded during the design service life due to the high critical chloride threshold of EC and SS; that is, the reliability indices of the pier remain constant, as shown in Figs.5(e) and 5(f).The first time-to-repair of the NPC-BS pier with respect to the serviceability and ultimate performance in the splash and tidal zone is 19.2 and 45.8 years, respectively.Due to the smaller moment value and the lower chloride content in the atmospheric zone compared with those in the splash and tidal zone,β1in the atmospheric zone during the design service life is greater thanβT1; thus,no repair is required for the capacity in the atmospheric zone, and the first time-to-repair of the serviceability performance in the atmospheric zone is 45.1 years, as shown in Fig.5(a).It is obvious that the serviceability performance controls the first time-to-repair.

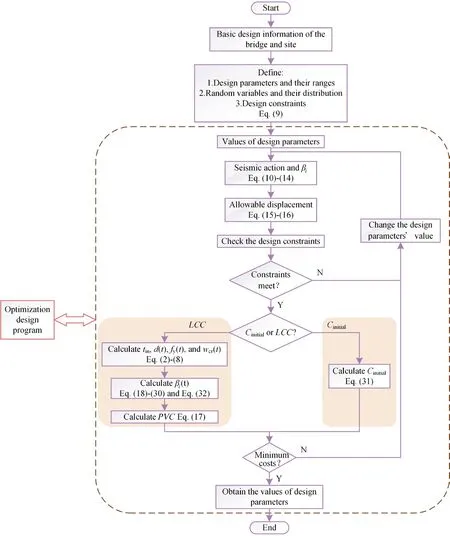
Fig.4 Reliability-based design optimization procedure for nonuniform corrosion bridge

Table 3 Rounded optimal design results with Cinitial and LCC as optimization objectives

The application of silane soakage to the NPC-Silane pier surface postpones the corrosion initiation and propagation phase.The cover thickness of the NPCSilane pier and NPC-BS pier is the same, and 10 years is assumed for the effective protection time for silane soakage; thus, there is a 10-year delay in the first timeto-repair between the NPC-Silane pier and NPC-BS pier for both the atmospheric zone and splash and tidal zone, as shown in Figs.5(a) and 5(c).Due to the lower permeability of HPC in this study, corrosion occurs only on the stirrups in the splash and tidal zone, which means that only patch repair is required in the splash and tidal zone, as shown in Fig.5(d).Figure 5 also indicates that the use of HPC, EC or SS will dramatically reduce the corrosion effects on both the serviceability and ultimate performance of the pier in this study.

Figure 6 shows the time-dependent reliability index of the pier considering the repair of Group A.As no corrosion occurs for the NPC-EC pier and NPC-SS pier during the design service life, as mentioned above, their time-dependent reliability index considering repair is the same as that in Figs.5(e) and 5(f), respectively, which is not shown in Fig.6.The results in Fig.6 show the pier needs as follows: eight patch repairs and zero overlay and 16 patch repairs and two overlays for the NPC-BS pier in the atmospheric zone and splash and tidal zone,respectively; seven patch repairs and zero overlay and 16 patch repairs and one overlay for the NPC-HSS pier in the atmospheric zone and splash and tidal zone,respectively; seven patch repairs and zero overlay and 13 patch repairs and one overlay for the NPC-Silane pier in the atmospheric zone and splash and tidal zone,respectively; and 3 patch repairs for the HPC-BS pier in the splash and tidal zone.In particular, Fig.6 indicates that the number of repairs for the NPC-BS, NPC-HSS and NPC-Silane piers are considerably greater than that of the others.

Fig.5 Time-dependent reliability index of the pier in Group A: (a) NPC-BS; (b) NPC-HSS; (c) NPC-Silane; (d) HPC-BS;(e) NPC-EC; (f) NPC-SS

Fig.6 Time-dependent reliability index of the piers in Group A considering repair: (a) NPC-BS in atmospheric zone; (b) NPC-BS in splash and tidal zone; (c) NPC-HSS in atmospheric zone; (d) NPC-HSS in splash and tidal zone; (e) NPC-Silane in atmospheric zone; (f) NPC-Silane in splash and tidal zone; (g) HPC-BS in atmospheric zone; (h) HPC-BS in splash and tidal zone

Figure 7 shows the time-dependentLCCs of the pier in Group A and Group B.For Group A, which takesCinitialas the optimization objective in the RBDO procedure,theCinitialandLCCof the NPC-HSS pier are the lowest.AlthoughCinitialof the NPC-BS pier is the lowest, except for NPC-HSS, itsLCCis the highest due to its regular repair, which leads to a substantial repair cost.On the other hand, for Group A, althoughCinitialof the NPCSS pier is the highest, it does not require repair actions;thus, itsLCCis much lower than that of the NPC-BS pier.For Group B, which takesLCCas the optimization objective in the RBDO procedure, the routine inspection and maintenance costs are taken into account in the design process, which results in theCinitialof NPC-BS,NPC-HSS, and NPC-Silane in Group B being slightly higher than that in Group A due to the increase in the amount of longitudinal rebar and concrete.On the other hand, the increase in the cover thickness reduces the repair frequency and the corresponding maintenance costs of NPC-BS, NPC-HSS, and NPC-Silane in Group B, which results in theLCCof these piers being lower than that in Group A.In particular, theLCCvalues of the NPC-BS, NPC-HSS and NPC-Silane piers in Group B are 7.8%, 6.8% and 1.6% lower, respectively, than those in Group A.HPC-BS, NPC-EC, and NPC-SS piers in Group A and Group B are the same in terms of the design parameters,CinitialandLCC, because during the design service life, for the HPC-BS pier, only slight corrosion occurs in the splash and tidal zone.For the NPC-EC and NPC-SS piers, no corrosion occurs, the routine evaluation and nondestructive inspection cost decreases with decreasing pier diameter, and the earthquake force decreases with decreasing pier diameter, which will lead to a reduction in the amount of longitudinal reinforcement and concrete and then reduces the cost.The decrease in the pier diameter will increase the axial force ratio and the pier top lateral displacement.These conflicting constraints lead to a rational outcome; that is,the same design parameters of HPC-BS, NPC-EC, and NPC-SS piers between Group A and Group B.Figure 7(b)also indicates that theLCCof NPC-Silane and NPC-EC piers is close to that of NPC-BS because the use of silane soakage or epoxy-coated steel increases theCinitialvalue of the pier, although it can delay the corrosion initiation and propagation phases and reduce the maintenance costs.

Fig.7 Time-dependent LCCs of: (a) Group A and (b) Group B

TheLCCof the NPC-HSS pier is the lowest in both Group A and Group B, which is due to the high strength of the steel, which can reduce the diameter of the pier under the constant axial load and further reduce the seismic force.Although the unit price of HSS is slightly higher than that of BS, the use of HSS will reduce the amount of steel and concrete and the corresponding seismic force; thus,CinitialandLCCwill be significantly reduced.Notably, the results obtained in this study are highly dependent on the values of the parameters (e.g.,the chloride concentration, chloride diffusion coefficient,chloride threshold value of the steel, material price,repair price, discount rate, and seismic parameters of the field).

8 Conclusions

To compare theLCCof different design materials for RC bridge piers under coastal corrosive environments and the difference in the design results by using different optimization objections, an RBDO procedure was conducted for the pier using six groups of materials,i.e., normal performance concrete (NPC) with black steel (BS) rebars, high strength steel (HSS) rebar,epoxy coated (EC) rebar, and stainless steel (SS) rebar(named NPC-BS, NPC-HSS, NPC-EC, and NPC-SS,respectively), NPC with BS with silane soakage on the pier surface (named NPC-Silane), and high performance concrete (HPC) containing 30% fly ash as a replacement of cement in mass with BS (named HPC-BS).A coastal RC bridge pier is selected to illustrate the procedure.According to the chloride concentration at different heights in the coastal environment, the pier is divided into three zones along its height: the submerged zone,splash and tidal zone, and atmospheric zone.The horizontal seismic force is considered as the lateral force acting on the top of the pier in the design process.

The selected bridge pier with a design service life of 100 years is designed for each group of materials using the RBDO technique.Considering probabilistic and deterministic constraints, the design optimization technique minimizes the cost while ensuring the performance.The reliability indices for the ultimate limit state related to the flexural capacity under constant axial load and serviceability limit state related to the concrete surface crack width are used in the RBDO procedure.In this study, the initial construction cost (Cinitial) andLCCare taken as the optimization objectives to design each group of materials and the design results of these two optimization objectives are named Group A and Group B, respectively.The design results of each group of materials are obtained, including the values of the design parameters,Cinitial, and time-dependentLCC.Based on theLCCfor each group of materials in Group A and Group B, the optimal design materials for the RC bridge pier in a coastal corrosive environment are determined,and the main conclusions are summarized as follows:

(1) The serviceability performance controls the first time to repair, thus increasing the cover thickness is an effective way to improve the corrosion resistance of the pier and reduce maintenance costs andLCC.

(2) Corrosion in the splash and tidal zone of piers is more severe than in the atmospheric zone, therefore more frequent repair is required.Furthermore, when EC and SS are used in the design, due to their high corrosion resistance, no corrosion will occur.

(3) Compared with usingCinitialas the optimization objective, usingLCCin the RBDO can reduce theLCCof the pier exposed to the coastal environment,especially for the NPC-BS, NPC-HSS and NPC-Silane piers, with a reduction inLCCof 7.8%, 6.8% and 1.6%,respectively, and with a slight increase inCinitial.

(4) TheLCCof NPC-HSS is the lowest among the six groups of materials in both Group A and Group B in this study, therefore NPC-HSS should be selected for the case in this research consideringCinitialorLCC.Note that the results of the optimization design strongly depend on the given parameters and constraints, such as the height of the submerged zone of the pier, the price of the materials, and the constraints, etc.

(5) The RBDO procedure withLCCas the optimization objective is an appropriate method for design and decision-making in corrosion management for piers in coastal environments.

This study focuses on the serviceability and strength issue of bridge piers with corroded reinforcement.Since corrosion not only reduces the yield stress but also the ultimate strain of reinforcing bars, the ductility issue needs to be considered in reliability analysis.As a continuation of this study, the ductility issue will be considered in a more comprehensive reliability-based design of the corroded bridge piers in future research.

Acknowledgement

The financial support from the National Natural Science Foundation of China (51921006, 51725801),Fundamental Research Funds for the Central Universities(FRFCU5710093320) and Heilongjiang Touyan Innovation Team Program are greatly appreciated.