粒子偏转的另类无穷解——带电粒子在匀强正三角磁场内外偏转问题研究

贾 平

(苏州科技城外国语高级中学 江苏 苏州 215000)

1 引言

带电粒子在磁场中运动的周期性回归问题(即带电粒子在不同形状的磁场中做周期性运动后回到初始位置的问题)是高中磁场类题目中的一个难点[1],因其能有效考查学生数理结合能力,读图形画图形能力、空间思维能力,此类问题成为高考的热点[2].命题人在命制带电粒子在磁场中的周期性运动问题时,需要明晰粒子运动轨迹,以确保命题准确和严谨.本文以2022年苏州高三上学期期末试卷压轴题为例,着重阐述带电粒子在三角形磁场区域中的运动轨迹,为高中物理教学提供有价值的参考.

【例题】如图1所示,边长为a的正三角形PMN区域内存在匀强磁场,磁感应强度大小为B、方向垂直于纸面向外,在PMN区域外存在足够大的匀强磁场,磁感应强度大小也为B、方向垂直于纸面向里.大量质量为m、电荷量为q的粒子,以大小不同的速度从MN的中点O垂直射入正三角形PMN区域内部,不计重力及粒子间的相互作用,一部分粒子经过磁场偏转后垂直MN回到O点.求:垂直MN回到O点的粒子速度的最大值.

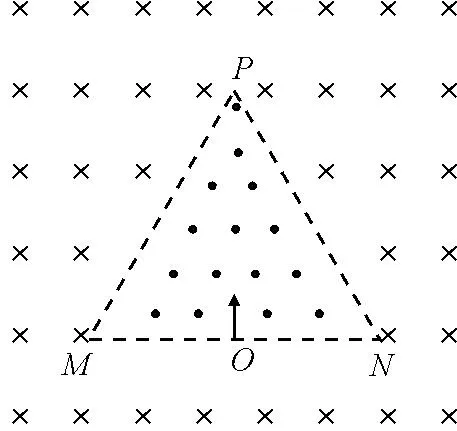
图1 例题题图

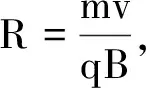
2 粒子的常规偏转情况

本节讨论θ为60°、120°、240°、300°的粒子常规偏转情况.

(1)θ=60°

当θ=60°时,粒子可能的偏转轨迹如图2所示.

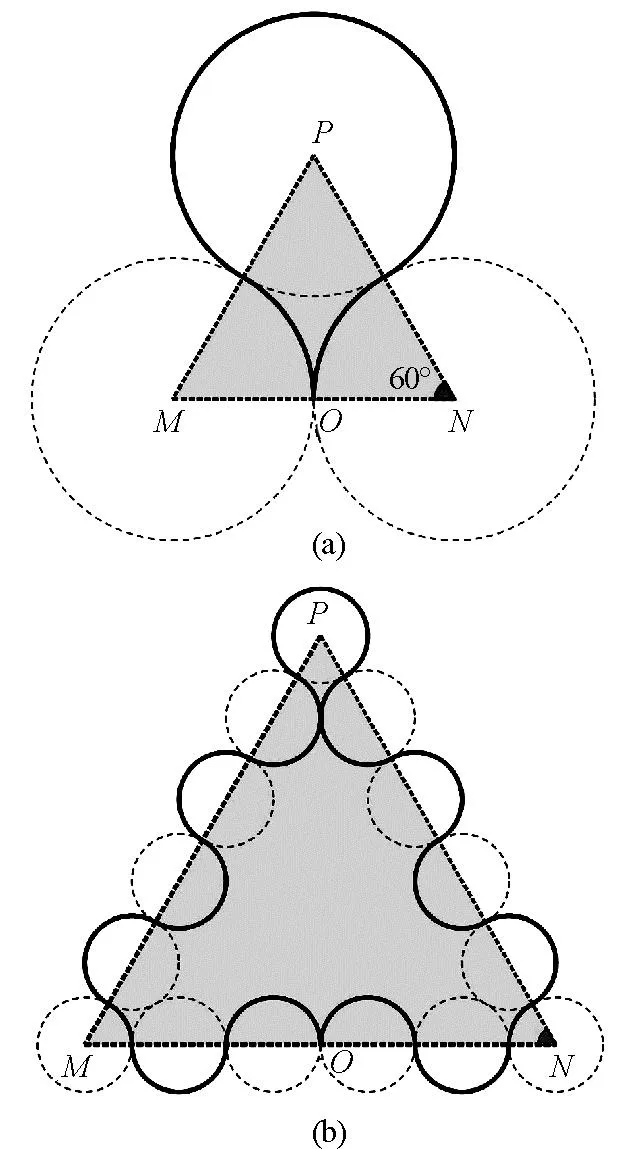
图2 偏转圆心角为60°时粒子的3次和15次偏转轨迹示意图

粒子运动半径R满足

该粒子可以垂直回到O点.运动半径为

粒子的初射速度为

粒子在磁场中的偏转总时间

轨迹与磁场边界的交点个数均为4n+1,粒子共有12n+3次偏转.

(2)θ=120°

当θ=120°时,粒子可能的偏转轨迹如图3所示.

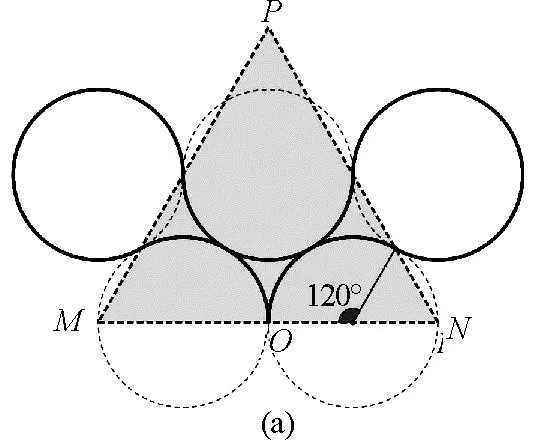
图3 偏转圆心角为120°时粒子的5次和25次偏转轨迹示意图

如图3(a)所示,粒子共有5次偏转,轨迹与磁场底边交点个数为1(不计回到O点),与侧边的交点个数为2.如图3(b)所示,粒子共有25次偏转,轨迹与磁场底边交点个数为5,与侧边的交点个数为10.

粒子运动半径R满足

该粒子可以垂直回到O点,运动半径为

粒子的初射速度为

粒子在磁场中的偏转总时间

粒子轨迹与三角形区域底边有4n+1个交点,与侧边的各有2(4n+1)个交点,共5(4n+1)次偏转.

(3)θ=240°

当θ=240°时,粒子的轨迹刚好能经过三角形区域底边M、N,如图4所示.

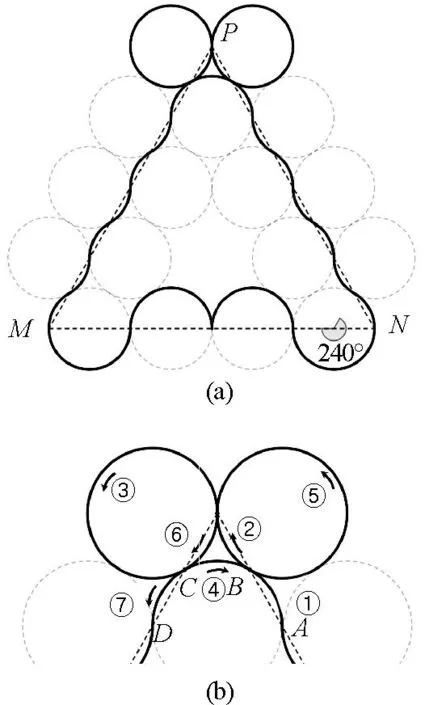
图4 偏转圆心角为240°时粒子的21次偏转轨迹示意图

粒子运动半径R满足

该粒子可以回到O点,运动半径为

则粒子的初射速度为

粒子在磁场中的偏转总时间

共(20n+21)次偏转.

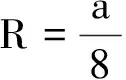
(4)θ=300°

当θ=300°时,粒子可能的偏转轨迹如图5所示.

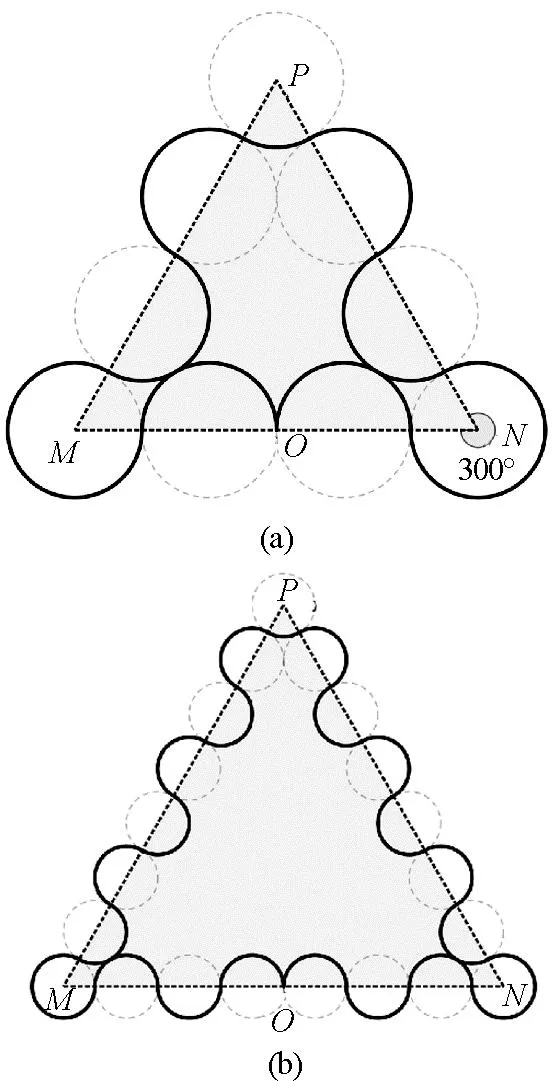
图5 偏转圆心角为300°时粒子的9次、21次偏转轨迹示意图

粒子运动半径R满足

粒子可以垂直回到O点,此时粒子运动半径为

则粒子的初射速度为

粒子在磁场中的偏转总时间

粒子与三边的交点数均为(4n+3),共3(4n+3)次偏转.

综上所述,当粒子运动半径满足

即三角形区域边长a与粒子运动半径R的比值为偶数倍时,带电粒子经过若干次偏转后总能垂直回到O点,但运动轨迹有所不同.

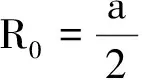
3 粒子的非常规偏转情况

本节首先分析带电粒子在磁场区域中5次偏转的其他情况,再构建模型,将该模型拓展到更多次偏转,考虑到偏转圆心角均不是特殊角度,因此称为非常规偏转.

(1)5次偏转情况分析

除了图3(a)给出粒子在磁场区域偏转5次的情况外,图6给出带电粒子偏转5次的其他情况.

图6 带电粒子经过5次偏转回到O点的非常规偏转

图6中,带电粒子从A1(O)点出发,经过①轨迹首次到达PN边A3点,而后沿着②的轨迹到达PM边的A5,再经过③轨迹到达A2,再经过④轨迹到达A4,最后经过⑤轨迹垂直回到A1点.粒子偏转轨迹与磁场侧边的交点数均为2,与底边交点数为1.粒子的偏转轨迹依次通过A1→A3→A5→A2→A4→A1.

假定正三角形区域边长a=1,通过Geogebra绘制图像,θ为28.377°,粒子的运动半径R≈1.267,即该情况下带电粒子能垂直回到O点且粒子偏转半径R大于3次偏转时的运动半径R0,此时粒子的出射速度大于v0.

(2)模型构建

带电粒子与三角形区域发生n次偏转(n为奇数),偏转轨迹与磁场区域的交点数记为:s-b-s,s表示轨迹与邻边交点个数,b表示轨迹与底边交点个数(不计粒子最后垂直回到O点),满足2s+b=n.

以5次偏转为例(n=5),底边交点个数b为1或3,则偏转轨迹交点有两种可能的类型:2-1-2和1-3-1.对于1-3-1型,由于粒子在三角形区域内外的运动半径相同,当粒子在底边有3次交替穿越时,不可能在两邻边只穿过1次,因此1-3-1类型的偏转轨迹不存在.有以下推论:轨迹与磁场邻边、底边交点个数差不大于2,即有|b-s|≤1.对于2-1-2类型,粒子以以下两种方式偏转:

1)A1→A2→A3→A4→A5→A1,如图2(a)所示,θ为120°,为常规偏转.

2)A1→A3→A5→A2→A4→A1,如图6所示,θ为28.377°,为非常规偏转.

(3)多次非常规偏转讨论

带电粒子在三角形区域内外经过7次非常规偏转情况为2-3-2型,即与底边有3个交点,与邻边各有2个交点,粒子轨迹与磁场区域3边交点的共有3种可能情况:1)A1→A2→A3→A4→A5→A6→A7→A1,粒子无法以该路径运动;2)A1→A3→A5→A7→A2→A4→A6→A1,如图7(a)所示,粒子运动半径R≈0.407,θ≈71.459°;3)A1→A4→A7→A3→A6→A2→A5→A1,如图7(b)所示,粒子运动半径R≈1.622,为7次偏转的最大半径,θ≈23.197°,此时粒子的出射速度大于v0.

图7 带电粒子经过7次偏转的非常规偏转轨迹

带电粒子9次非常规偏转情况为3-3-3型,粒子偏转共有4种可能情况:

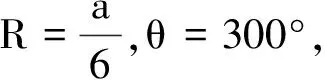
2)A1→A3→A5→A7→A9→A2→A4→A6→A8→A1,粒子的偏转轨迹如图8(a)所示,粒子运动半径R≈0.275,θ=105.184°;

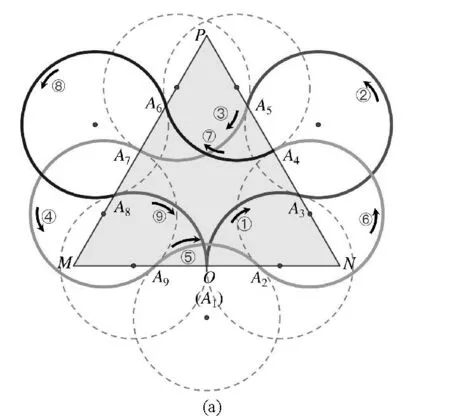
图8 带电粒子经过9次偏转的非常规偏转轨迹

3)A1→A4→A7→A1,该情况恰好变成3次偏转情况,θ=60°,如图2(a)所示,为常规偏转;

4)A1→A5→A9→A4→A8→A3→A7→A2→A6→A1,粒子的偏转轨迹如图8(b)所示,粒子的运动半径R=2.049,θ=19.107°,为9次偏转的最大运动半径.

当带电粒子在三角形区域内外发生11、13、15次非常规偏转时,偏转路径、偏转半径和偏转圆心角如表1所示.

表1 带电粒子在磁场中11、13、15次非常规偏转参数

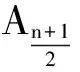
4 结论

本文根据带电粒子首次偏转到PN边界的圆心角是否为特殊角,将偏转轨迹分成常规和非常规两类,对粒子的非常规偏转进行建模并归纳总结:若正三角形内外分布着两个方向相反但磁感应强度相同的匀强磁场,当带电粒子从正三角形底边垂直出射时,不存在能垂直回到原点的最大粒子速度.

本题模型符合命题设计要求,具有创新性,切入角度新颖,能够很好地考查学生的思维和学科素养.但在命制三角磁场内外偏转问题时,需要对带电粒子可能的运动轨迹有所明晰,以确保命题准确和严谨性.对该问题的研究也为教师开展教学研究和思考提供一定的借鉴.