缺失数据下区间数据均值的估计与检验

赵志文,于 月,姜 珊

(吉林师范大学 数学与计算机学院,吉林 四平 136000)

0 引言

随着大数据时代的到来,数据也变得更加多元化,对于一些实际问题,所获得的观测数据通常只能用某一取值范围来表示,例如某城市一天的气温和湿度的变化范围、股票的涨幅情况等,该数据称之为区间数据.区间数据的统计推断一直也是统计学家关心的热点问题之一.

针对区间型数据的建模及模型的统计推断问题,尹逊汝[1]研究了区间数据下线性模型的参数估计问题,同时证明了估计量的相合性;王金婵等[2]针对区间数据建立了区间数据回归模型并给出了模型参数的估计方法;邓文丽等[3]讨论了区间数据下指数分布参数的矩估计问题,通过矩方法得到了区间截断情况下参数的两个矩估计,并通过这两个矩估计的关系得到了一个更优的估计,最后利用矩估计的渐近性质,进一步得到了两种区间截断情况在大样本下参数的置信区间;Blanco-Fernández等[4]讨论了自变量和因变量均为区间值数据时简单线性回归模型的参数估计问题,并给出了模型参数的最小二乘估计,同时证明了估计量的强相合性;Calcagnì等[5]基于符号回归分析方法,提出用新的回归模型来对区间值变量进行分析;2012年,Blanco-Fernández等[6]基于最小二乘估计的渐近分布,讨论了区间值线性回归模型参数置信集的构造问题;此外,Sinova等[7]基于区间值数据的运算性质建立了区间值回归模型,并且利用最小二乘方法考虑模型参数的估计问题.

由于在实际观测中经常存在数据缺失,因此缺失数据的估计和检验问题一直是统计学家们关心的热点问题之一.田萍等[8-9]利用EM算法,研究了缺失数据条件下零均值AR(p)模型和ARMA(1,1)模型的参数估计问题;马明月等[10]讨论了部分缺失数据两个双参数指数总体的参数估计问题;赵志文等[11]研究了具有部分缺失数据的两个几何分布总体中的参数估计问题以及两总体参数相等的假设检验问题;陈菲等[12]讨论了部分数据缺失时两个Weibull总体的参数估计和关于总体相同的似然比检验问题;龙兵等[13]研究了在样本数据缺失下Pareto分布的参数估计和假设检验问题;刘银萍等[14]针对于缺失数据情形下两个泊松总体的参数估计问题以及两总体参数相等的假设检验问题进行了进一步的讨论;徐圣楠等[15-16]利用矩估计的方法,研究在缺失部分数据的情况下混合瑞利分布总体及混合拉普拉斯分布中总体参数的估计问题;王敏会[17]在此基础上,讨论了具有部分缺失数据混合几何分布总体的参数估计问题.本文进一步考虑数据存在缺失并且缺失概率未知时的区间数据均值的估计与检验问题.

1 缺失数据下区间均值的估计

设X是随机区间总体,{X1,…,Xn}是独立同分布的随机样本,令

证明由独立同分布的大数定律可知

(1)

同理可证

(2)

下面的引理给出了证明极限分布为正态分布的随机向量函数依分布收敛于正态分布的方法.

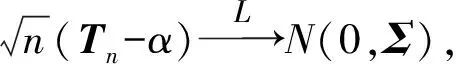
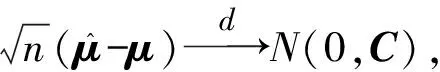
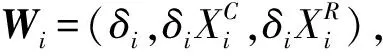
E(Wi)=(P,PμC,PμR).

由独立同分布的多元中心极限定理可知

记

其中

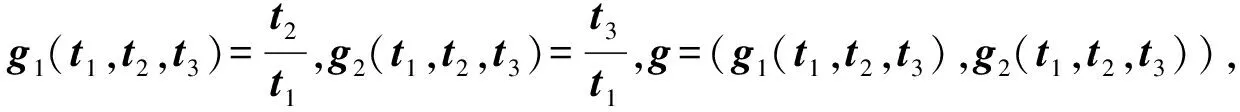
易知

令

θ=(θ1,θ2,θ3)=(p,pμC,pμR),

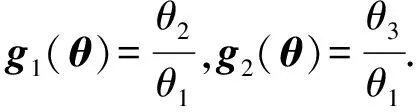
注意到

进而可得

利用引理1,经过简单的代数运算可知

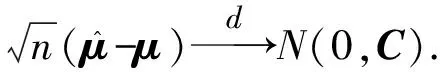
2 缺失数据下区间均值的检验

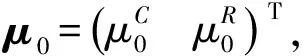
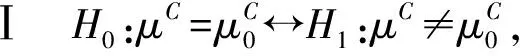
检验ⅢH0:μ=μ0↔H1:μ≠μ0,

检验Ⅰ和检验Ⅱ分别考虑区间中心和区间半径是否等于某一常数的检验问题,检验Ⅲ则是同时考虑区间中心和区间半径是否等于某一常数的检验问题.

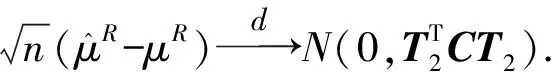
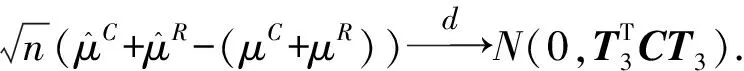
利用Cramer-wold定理易知推论1、推论2和推论3成立.为对上述检验问题构造检验统计量,考虑C的估计,令

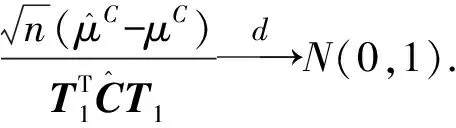
首先考虑区间中心是否等于某一常数的检验问题Ⅰ.构造检验统计量

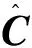
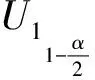
其次考虑区间半径是否等于某一常数的检验问题Ⅱ.构造检验统计量

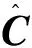
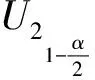
最后同时考虑区间中心和区间半径是否等于某一常数的检验问题Ⅲ.构造检验统计量

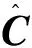
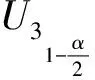
3 随机模拟

对于检验问题Ⅰ,表1给出了原假设为真时接受原假设的概率,表2给出了备择假设为真时拒绝原假设的概率.对于检验问题Ⅱ,表3给出了原假设为真时接受原假设的概率,表4给出了备择假设为真时拒绝原假设的概率.对于检验问题Ⅲ,表5给出了原假设为真时接受原假设的概率,表6给出了备择假设为真时拒绝原假设的概率.

表1 缺失概率为0.1时原假设成立的条件下接受原假设的概率

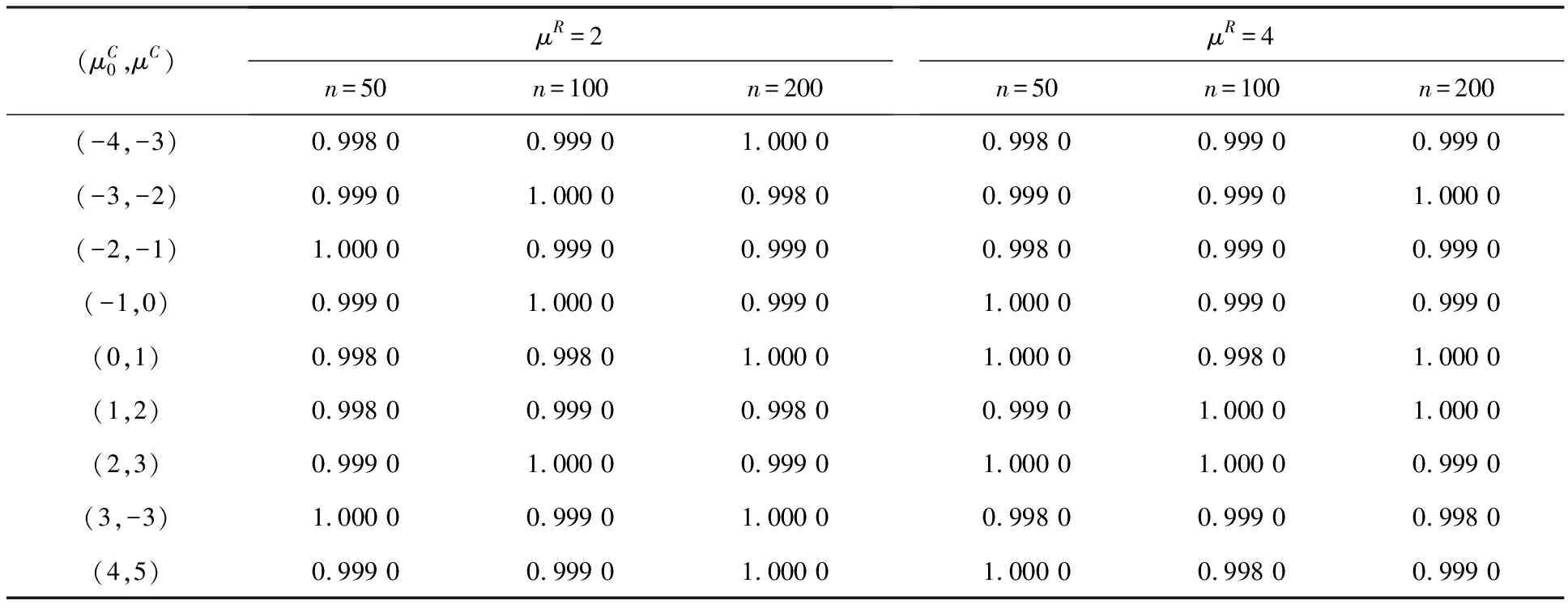
表2 缺失概率为0.1时备择假设为真时拒绝原假设的概率

表3 缺失概率为0.1时原假设成立的条件下接受原假设的概率

表4 缺失概率为0.1时备择假设成立的条件下拒绝原假设的概率

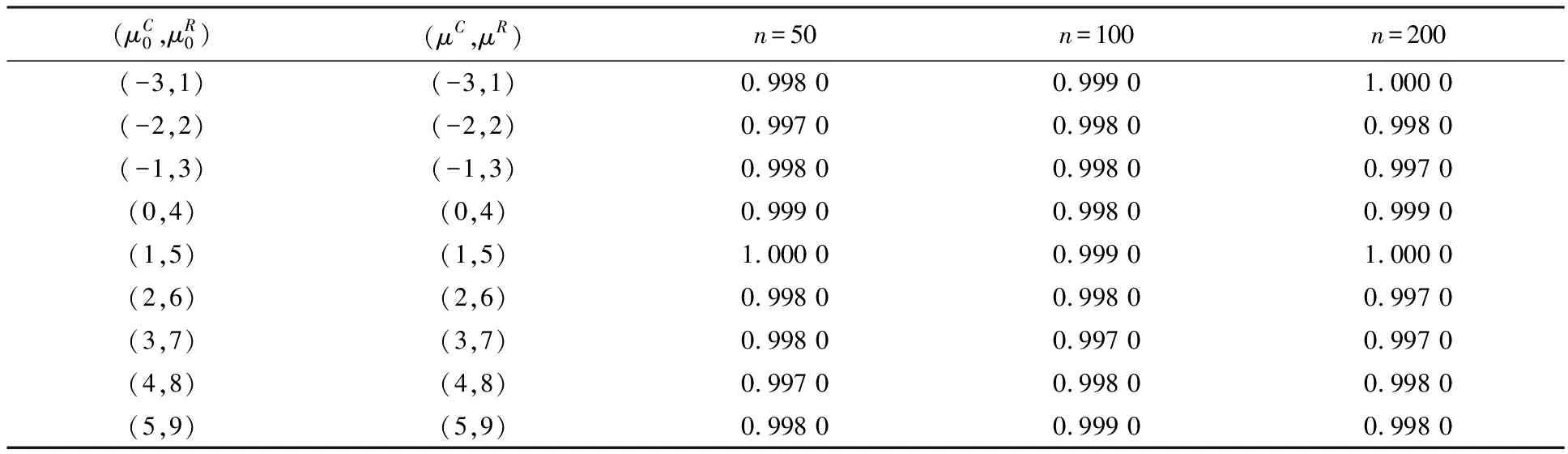
表5 缺失概率为0.1时原假设成立的条件下接受原假设的概率

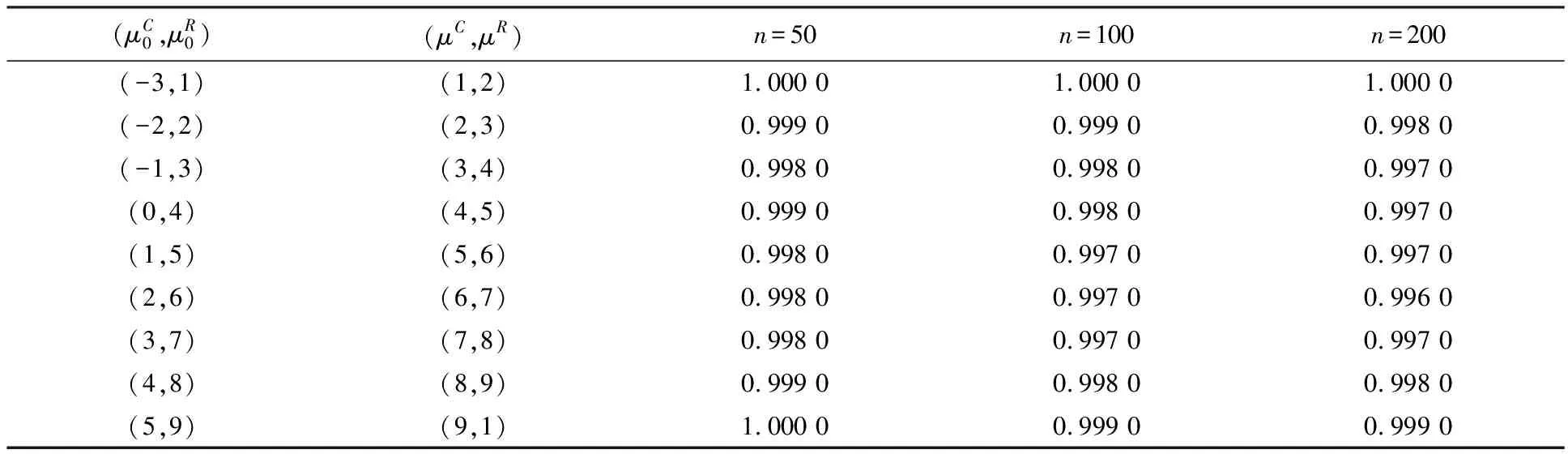
表6 缺失概率为0.1时备择假设成立的条件下拒绝原假设的概率

从表1—6的模拟结果可以看出,随着参数取值的变化,无论原假设成立的条件下接受原假设的概率还是备择假设成立的条件下拒绝原假设的概率都是接近1的,因此说明上述三个检验方法具有可行性.此外,从模拟结果可以看出,模拟结果不受参数变化的影响,这说明所给出的检验方法具有一定的稳健性.

4 结语

本文讨论了缺失数据下区间数据均值的估计与检验问题,利用矩估计方法给出区间中心和半径均值的估计,在此基础上进一步对区间中心均值、区间半径均值相关的检验问题进行研究,与以往研究不同的是该统计推断方法可以在数据存在缺失的条件下使用.该研究结果进一步丰富和发展了区间数据的统计推断理论,为进一步研究缺失数据下区间数据的统计推断问题奠定了基础.