基于力觉伺服轨迹规划的磨抛工业机器人曲面跟踪控制研究

胡建玥

(福建省特种设备检验研究院,福建 福州 350007)

0 引言

工业机器人在自由曲面进行磨抛作业时,工业机器人的运动轨迹往往会受到一些附加约束条件的限制,需要控制末端工具中心点TCP(tool center position)精确跟踪曲面上规划的既定轨迹来保证磨抛工件的表面加工质量。然而在实际应用中,工件在磨抛前往往存在尺寸误差,工业机器人末端工具需要随着磨抛曲面实时调整工业机器人运动轨迹,使末端工具与工件之间的作用力始终保持在一定范围,以保证工业机器人磨抛过程的磨抛质量[1]。

在工业机器人磨抛应用中基于STL模型生成加工轨迹的方法已被广泛使用[2]。当前,对自由曲面的加工轨迹的规划主要包括投影法、等参数法、截平面法等[3]。WALCZYK等[4]针对STL曲面模型,采用截面法生成加工轨迹,探讨了轨迹的处理算法并生成连续的加工轨迹。徐金亭等[5]在STL曲面模型中,对模型曲面进行局部拟合并利用等残留高度法生成连续的加工轨迹。赵萍等[6]则面向数控机床加工,重点研究了STL模型的刀具加工轨迹、刀具路径规划等问题。

上述方法对于曲面模型的轨迹规划问题有一定的借鉴意义,但是无法避免产生曲线偏置的干涉情况,并且未结合轨迹运动控制对工业机器人磨抛运动系统进行全面系统研讨。本文基于工件的STL模型,拟合生成了工业机器人的磨抛轨迹,另外结合力/位置控制方法,对工业机器人磨抛作业进行自由曲面跟踪控制研究,并通过实验平台进一步验证了该方法的准确性和稳定性。

1 实验方法

本文采用的工业机器人磨抛系统包括一台链式串联工业机器人、多维力传感器、电动主轴、磨抛工具、待磨抛工件以及相应的固定底座(图1)。此外,工业机器人磨抛作业平台还包括主机控制系统和力信号采集装置。其中,6D力传感器采集的力信息利用数据采集卡传输至控制主机,控制主机与工业机器人双向连接;工业机器人的工作状态实时反馈给控制主机,控制主机综合处理工业机器人的状态信息和末端受力信息,计算出工业机器人的位姿调整值并实时将轨迹运动指令传输至工业机器人,控制工作台沿运动轨迹作业。

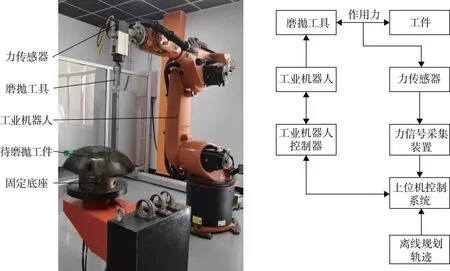
图1 磨抛系统平台及原理

1.1 自由曲面轨迹规划

对曲面拟合的方法主要包括Bezier曲面、B样条曲面、NURBS曲面、Coons曲面等[7]。考虑到单个三角平面片中信息有限,仅有3个顶点的位置及所在位置的法向矢量估计。因此本文将采用多种Bezier三角自由曲面无限拟合的方法对三角平面片进行自由曲面拟合,如图2所示。

图2 Bezier三角曲面拟合

图2中,三角区域内任意一点都可以利用面积坐标来表示,G为自由三角区域ABC任一点,其面积坐标(u,v,w)与面积值s,求得三角形GBC面积为

(1)

由多个三角平面片拟合成的三角自由曲面方程为

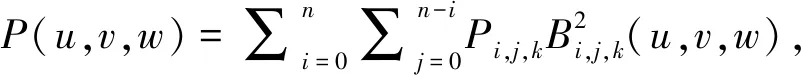
(2)

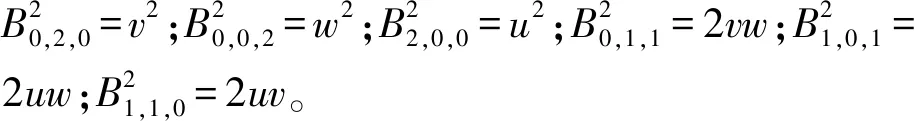
考虑到STL三角平面片中的原始数据包括顶点坐标和法向矢量,如图3所示;通过对曲线Hermite插值生成许多中间点,进而构造二次曲面片的拟合点P1,1,0、P0,1,1和P1,0,1。对于曲线上的两个端点及其切向量P0、P1,则曲线方程的三次Hermite形式为

图3 Bezier曲面的拟合点

P(t)=(2t3-3t2+1)P0+(-2t3+3t2)P1+(t3-2t2+t)P′0+(t3-t2)P′1,t∈[0,1]

(3)

位置点的切向量估计可以通过两点之间的连线及法向矢量进行求解,已知轨迹上的两点P0和P1及其法向量n0和n1,v12为P0指向P1的单位向量,则P0和P1的切向量为

(4)

将式(4)代入式(3)后,求解出曲线的中点P1,1,0、P0,1,1、P1,0,1,将曲线的端点及中点代入式(2),求解出拟合的三角曲面的曲面方程,实现对三角平面片的曲面拟合。

通过Beizer三角曲面拟合方法对STL模型进行曲面拟合获得对原始曲面的近似拟合,进而在拟合曲面上生成磨抛轨迹。常用的加工自由曲面轨迹生成方法包括等截面法和等参数法等,其中,等参数法由于计算简单、轨迹生成速度快等优点被广泛应用于加工轨迹的生成过程[8]。如图4所示,等参数法的本质是:在已知曲面上的一个点Pi沿某一方向ti,在曲面上找到一点Pi+1,使得与Pi的Pi+1空间直线距离为S。

图4 轨迹生成原理

在传统的曲面轨迹规划中,一般采用轨迹偏置的方法生成全部轨迹[8],但这种方法常会出现偏置曲线相互干涉的问题,处理复杂。针对曲线偏置方法的不足,本文根据曲线路径曲率的变化,自适应调节控制点的间距,同时避免曲线偏置时的干涉问题,具体实现方式如下。

在曲线偏置中,曲线的局部形状可以近似为圆弧,相邻曲线近似为同心圆。如图5所示,已知曲线Ci偏置获得曲线Ci+1,曲线Ci上一点Ci(tj)偏置设定距离l获得曲线Ci+1的曲线控制点Ci+1(tj)。由Ci+1(tj)沿切向偏置控制点距s获得Ci+1(tj+1)′,由Ci+1(tj+1)′寻找Ci上的最近点Ci(tj+1),再由Ci(tj+1)偏置l获得Ci+1(tj+1)。

图5 偏置曲线生成机理

为便于利用计算机的计算优势,对参考曲线Ci进行曲线离散化,由曲线上的密集点集代替曲线作为有序参考曲线点集,Ci(tj)生成Ci+1(tj)后可将Ci(tj)之前的子点集删除,简化计算。由于轨迹生成过程是按点生成的,每个点生成过程中都已经确保不与其他轨迹产生干涉,进而生成无干涉的轨迹。本文基于螺旋式轨迹生成磨抛轨迹,如图6所示,螺旋式磨抛轨迹实现了自由曲面轨迹规划,加工完成仅需抬刀处理,加工轨迹连续且满足轨迹规划要求,通过三维重构减小了模型误差。

图6 螺旋式磨抛轨迹

1.2 工业机器人曲面跟踪控制

为了使工业机器人磨抛时保持一个恒定的接触力,选择图7所示的间接力/位置混合控制结构[9]。

图7 力/位置混合控制

为了获得更快的工业机器人磨抛系统响应速度,位置控制环采用PD控制,同时为进一步有效地消除稳态误差,力控制环采用PI控制,因此:

(5)

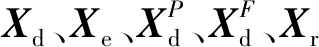
当工业机器人采用速度控制模式,可得:

(6)

设工业机器人当前末端的位置和速度分别为P0和v0,工业机器人跟踪的目标点位置为P1(图8),则期望的速度矢量为v01、verr为v0与v01的速度矢量偏差。若磨抛位置控制器采用PD控制,将速度矢量偏差verr作为PD控制器的输入信号,输出的偏差信号v′err与期望速度矢量v01合成为位置速度控制量v;通过每个控制周期重新计算v,工业机器人末端将沿图8中的虚线移动至目标点。

图8 工业机器人末端位置的速度控制示意

工业机器人末端点实时姿态可通过固连在末端点的坐标系来表示。本文讨论单个坐标轴的姿态跟踪控制算法,如图9所示,工业机器人末端TCP当前的姿态坐标轴为n0,目标姿态的坐标轴为n1,等效转轴矢量为f0,则工业机器人末端姿态运动的期望等效转轴矢量为f01。等效转轴矢量为姿态坐标轴当前的转动轴和转动速度合成:

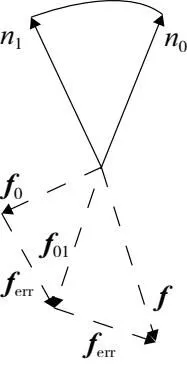
图9 末端姿态的速度控制

(7)

为实现磨抛机器人的力/位置混合控制,需要对磨抛机器人末端的运动进行分解,在作用力控制空间上采用力的作用位置控制方式,而在位置控制空间仍采用位置控制的方式,通过速度控制方式实现工业机器人末端的力/位置混合控制。如图10所示,在工业机器人末端TCP坐标系下,z轴设为力控制空间,其余空间为位置控制空间。当前位置跟踪控制系统的计算速度矢量为v,将速度矢量向力控制空间z轴和其余空间xOy平面分解为vz和vxy;由于z轴为力控制空间,根据当前接触力信息计算出TCP轨迹的修正速度vFz。因此z轴的速度矢量被替换为速度矢量vFz;将z轴矢量vFz和矢量vxy合成为力/位置混合控制,矢量v′,实现工业机器人末端的力/位置混合控制,其中力控制速度矢量vFz可由式(7)求得。

图10 位置速度在力空间的分解与合成

类似于位置速度在力空间的分解与合成,在工业机器人末端TCP坐标系中,设y轴为力控制空间。将姿态跟踪控制器计算的矢量f向力控制空间的y轴分解为fy和fxz,用实时接触力信息计算的姿态速度矢量fFy与位置控制的姿态速度矢量合成为姿态的力/位置混合控制矢量f′,如图11所示。

图11 姿态速度在力空间的分解与合成

因此,本文通过设计位置跟踪控制器和姿态跟踪控制器,在引入力控制后的姿态与位置控制器上实现对磨抛轨迹上点的跟踪,针对磨抛过程中的恒力控制要求,采用间接力/位置混合控制算法,保证机器人的轨迹跟踪。针对机器人控制器一般不对外开放的特殊性,采用上位机+机器人控制器的控制架构,利用机器人速度控制指令实现机器人的轨迹跟踪控制。

2 实验结果与讨论

2.1 轨迹跟踪实验验证

在工业机器人磨抛作业的脚本指令中,提供一种通过实时规划机器人末端的运动速度,保证工业机器人末端速度恒定的一种控制指令speedl,speedl运动控制指令格式为“speedl(xd,a,t)”。其中:“xd”为工业机器人末端TCP的速度值,包括末端空间位置移动速度“xdp(m/s)”和姿态调节速度“xda(rad/s)”;“a”为加速度;“t”为指令运行时间。实际跟踪的轨迹一般是非规则曲线,对于非规则曲线可以通过分段圆弧对曲线进行近似[10-11]。为此,对圆弧轨迹进行轨迹跟踪实验,实验的圆弧轨迹参数如表1所示,设置跟踪进给速度为10mm/s。实验结果如图12所示,工业机器人的运动速度控制在10mm/s,跟踪误差只有不到0.3mm,控制效果与精度良好。

表1 圆弧轨迹的参数

图12 速度与跟踪误差

2.2 力/位置混合控制实验验证

根据力/位置混合控制方法,将工业机器人的加工运动轨迹空间分解成位置控制和力控制两个空间。工业机器人在力控制空间上对接触摩擦力、平台抖动等外力误差的响应直接影响工业机器人磨抛加工过程中的恒力控制性能。通过对外界力误差反馈为工业机器人末端工具的速度修正值,实现工业机器人的对运动轨迹和作用力误差的修正。实验过程中,将工业机器人工具坐标系的z轴设为力控制轴,目标接触摩擦力设置为20N。对工业机器人磨抛作业进行单轴的力控制实验,工业机器人在单轴力控制模式下,工业机器人末端工具与工件接触并保持接触力稳定的响应时间在0.5s以内。稳定后的接触摩擦力值大部分集中在目标期望接触摩擦力的±3N区间内,实验表明力控制方法具有稳定性,如图13所示。

图13 目标接触力为20N的力响应

2.3 曲面跟踪控制实验验证

通过规划出工业机器人加工轨迹,使控制机器人跟踪规划的轨迹,进而实现加工自由曲面跟踪控制,如图14所示。图中黑色轨迹是加工过程的轨迹位置,而蓝色的是轨迹上的指向向量,即工具的主轴轴向;绿色和红色轨迹分别为开始及结束时的轨迹引导点,防止工业机器人与工件产生不必要的干涉接触(本刊黑白印刷,相关疑问咨询作者)。

图14 离线规划的部分加工轨迹

在加工过程中,通过沿轨迹点的法向方向偏置一定距离,使得工业机器人加工轨迹与工件产生接触,进而产生加工过程的接触力。设加工的目标接触力F=20N,工具的弹性模量为k=5 000N/m2则轨迹的偏置量为D=F/k=0.004m=4mm。

将轨迹点沿各自的法向负方向偏置4mm获得新的轨迹,作为工业机器人预期的加工轨迹。为了保证加工过程中的接触力恒定,引入力控制技术对工业机器人加工轨迹进行修正,同时保证工业机器人进给速度的恒定。在工业机器人加工轨迹的z轴上(即电动主轴方向)采用力控制,而在其余自由度上采用位置控制,实验结果如图15所示。加入工业机器人力控制技术后,z轴末端的受力能够控制在±4N范围内,但是加工过程中仍有几个波峰。对加工轨迹进行分析,可知这几处的波峰主要是加工轨迹有6处曲率变化较大轨迹,工业机器人在恒定速率的加工过程中,作用力响应延迟使得机器人末端受力变小。

图15 工业机器人末端z轴力

3 结语

本文就工业机器人提出一种自由曲面磨抛轨迹自动生成方法,重点对工件STL模型进行Bezier三角曲面拟合,进而得到拟合曲面方程。其次,利用等参数法和曲线偏置的方法,得到工业机器人进行跟踪控制的全部轨迹,并对加工工件的自由曲面生成了螺旋式磨抛轨迹。同时,补充了曲面偏置的方法,通过轨迹的转换算法生成了机器人加工过程中磨抛轨迹位移曲线,解决了曲线偏置时的干涉问题,并通过间接力/位置的控制方法进行曲面跟踪控制。最后通过磨抛实验平台对机器人力觉伺服轨迹规划方法进行实验验证,一是在跟踪进给速度为10mm/s的情况下曲面跟踪误差只有不到0.3mm,证明了利用机器人速度控制指令实现机器人的轨迹跟踪控制效果与精度良好;二是工业机器人在单轴力控制模式下,目标接触摩擦力为20N时,工业机器人末端工具与工件接触并保持接触力稳定的响应时间在0.5s以内,稳定后接触摩擦力值在目标接触摩擦力的±3N区间内,证明了力控制方法具有稳定性;三是加入工业机器人力控制技术后,z轴末端的受力能够控制在±4N范围内,证明了本文方法的有效性。本文对机器人力控制的轨迹规划展开的研究,对于曲面跟踪控制的研究具有一定意义。