基于二次摄动法的SMA层合梁非线性自由振动分析

张配

(西安铁路职业技术学院 机电工程学院,陕西 西安 710026)

0 引言

复合材料有着优异的力学特性,使得复合材料制成的结构部件被广泛应用于机械工程的各个领域,如交通运输、制造和汽车等领域[1]。形状记忆合金(SMA)在受热的情况下会表现出很大的形变,因而可以将SMA应用到复合材料领域,实现材料刚度的调节。研究显示,内嵌SMA的层合板减小了变形挠度[2-3]。SHIAU等[4]的研究得到SMA的体积分数和预应变的增加会产生更多的恢复应力,从而增加层合板的刚度。ASADI等[3]的研究显示夹层板的热惯性稳定性可以通过SMA丝的体积分数和SMA纤维中的预应变来控制。MAHABADI等[5]的研究显示方形SMA层合板比有相同长度的矩形板具有更高的基频。

二次摄动用于结构的屈曲与振动分析,有不少文献关于二次摄动法的应用。张大光[6]得到高次摄动解适于描述梁的深度后屈曲和深度非线性弯曲。佘桂林[7]对比了KBM法和二次摄动法在求解大幅振动时的差异,得到二次摄动法更加符合工程实际。BABAEI等[8]用二次摄动法研究了3种不同的剪切变形梁在弹性支承上的振动特性。文献[9] 中二次摄动法的引入可以不增加计算量,得到结构动力响应的较精确估计。GAO等[10]用二次摄动法得到非局部应变理论和应变梯度理论对线性和非线性有相反的影响频率。SHEN、HUI等[11-14]研究表明FGM材料的FG-X对称分布可以显著提高频率,得到当温度升高或基础刚度降低时,固有频率降低,但非线性频率比增加,且Voigt与Mori-Tanaka模型间的结果差异更小。BABAEI等[15]分析了受热传导、线性温度变化、均匀温升等不同类型热环境的FGM管。

通过对现有文献的梳理,可知尚没有研究使用二次摄动法分析SMA层合结构的非线性振动特性。本文考虑了温度变化和不可移动简支边界条件的SMA层合梁。使用Von-Karman大变形理论描述梁位移与应变的关系,用Brison模型描述了不同温度下SMA的恢复应力和马氏体体积分数。使用Hamilton原理建立了SMA层合梁的动力学方程。采用二次摄动法求解这些方程。研究了SMA不同初始应变、体积分数、铺设角度不同时频率比的变化。

1 系统建模

1.1 SMA本构方程

根据Brison模型,使用Reuss方法计算SMA的Young′s模量[2]。考虑零初始条件下,SMA丝恢复应力为

σr=ES(ξ)(ε-εLξS)+ΘΔT

(1)

式中:σr是SMA丝恢复应力;ES(ξ)为弹性模量;ε、Θ分别是SMA的应变和热弹性系数;εL为SMA最大残余应变;ξS为应力诱发的马氏体相变体积分数;ΔT(相对温度)是加热温度与初始温度的差值。

1.2 系统控制方程

图1为SMA的层合梁示意图。使用Vigot模型描述SMA/石墨/环氧树脂层的物性参数。需要说明的是,材料物性参数的下标“m”和“s”分别表示基体材料(石墨/环氧树脂)和SMA。梁的横截面为矩形,宽度为B,总厚度为H,梁的长度为L,层数为Nl,各层纤维是对称布置的。层合梁受到横向均布载荷q,梁在弹性地基上,并处于热环境中。

图1 SMA层合梁示意图

依据Reddy高阶剪切理论以及Hamilton原理,可得系统动力学方程为:

(2)

(3)

式中:I是广义惯量;X是梁的无量纲坐标;W是梁的无量纲横向位移;Φ是梁的无量纲截面转角;t是无量纲时间;NT是SMA的热力;Nr是SMA的恢复力。

2 振动分析

本节采用分析法推导出SMA层合梁非线性屈曲和自由振动的响应。在本节中,采用二次摄动法进行分析[16],解为

(4)

式中:ε是一个小扰动参数,有τ=εt;n是级数的项数,在本文中取n=3。依据摄动参数εi合并同类项,获得如下微分方程。

一阶摄动方程表示为

(5)

(6)

二阶摄动方程表示为

(7)

(8)

三阶摄动方程表示为

(9)

(10)

由满足简支边界条件的解,并使用Galerkin法得到:

Γ3(εA10)3+…

(11)

上式的系数分别为:

(12)

对于自由振动λq=0,可得系统固有频率为

(13)

式中:ωNL为非线性固有频率;ωL是线性固有频率;wmax为变形位移的最大值。

3 数值计算

层合梁的长度L=0.2m,宽度B=0.1m,厚度H=0.01m。每一层的厚度是相等的。SMA的材料参数见文献[2] 。初始情况下ξT0=0,T0=20 ℃,σ0=0,ε0=0.2%,VS=2%。式(13)可以计算出系统的线性固有频率,非线性频率与线性频率之比。

表1显示不同算法所得SMA梁的无量纲线性频率。可知本文方法所得的线性频率与Ritz[16]、GDQ[17]的结果差值很小,本文方法和Ritz法相差很小,与GDQ相差较大。当VS较小时频率随温度的增大而减小,当VS较大时线性频率先减小后增大再减小,其变化趋势与文献[3] 一致。通过不同方法的对比,证明本文方法是正确的。

表1 不同求解方法的无量纲线性频率

SMA层合梁的中部挠度与频率比(非线性频率与线性频率之比)如图2所示。SMA体积分数VS=2%,初始应变ε0=0.4%,长高比L/H=20,不考虑地基的刚度。结果和预期的一样,温度增加时频率比增加,线性固有频率减小。这是因为所选取的温度范围内,热应力比SMA恢复应力大得多,结构的刚度主要受热应力的影响,而热应力使梁的刚度减小。

图2 温度变化时的频率

图3中SMA体积分数VS=10%,初始应变T=120 ℃,长高比L/H=30,不考虑地基的刚度。SMA初始应变增加,频率比减小,线性频率增加。温度不变时结构热应力不变,结构刚度的变化主要受SMA恢复应力的影响,初始应变越大,SMA恢复应力越大,导致系统刚度增加。

图3 初始应变变化时的频率

图4中SMA初始应变ε0=0.4%,T=150 ℃,长高比L/H=30,不考虑弹性地基的作用。SMA体积分数增加,频率比减小,线性频率减小,主要原因是SMA体积分数越大,结构中的金属相组分越多,系统的刚度越大,等效密度也增大,这样广义惯量的增加对系统频率的影响大于刚度。

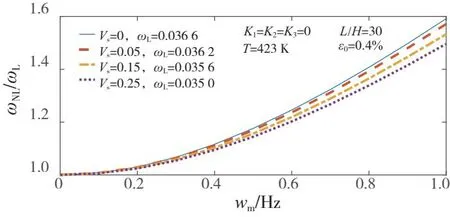
图4 体积分数变化时的频率

图5是长高比对频率的影响曲线。长高比L/H增大时频率比增大,线性频率减小。这是由于SMA梁跨度增大使柔度增加所导致的。L/H越大时系统的非线性特性越显著。观察到L/H比对频率比的影响在较低的长高比下更为明显。

图5 长高比变化时的频率

图6是SMA角度对频率的影响曲线,可以看出SMA铺设角度越大,梁的线性固有频率越小,而频率比越大。这是由于随着SMA铺设方向与主方向之间角度的增加,系统的总刚度降低导致的。

图6 SMA角度对频率的影响

4 结语

利用Hamilton变分原理,建立了SMA层合梁的动力学方程。使用二次摄动法研究了系统的自由振动特性,得出如下结论。

1)较低的温度下,热应力占主导,温度上升使得线性固有频率下降。

2)初始应变越大SMA恢复应力越大,系统刚度越大;SMA体积分数越大,系统的刚度、惯量同时增加,惯量的增加大于刚度的增加。

3)长高比增大时,频率比增大,线性频率减小;SMA铺设方向与主方向夹角的增加,导致线性频率下降,而频率比上升。