基于三周期极小曲面的多孔结构力学性能研究

张曦,丁力平,吴沛豪

(南京航空航天大学 机电学院,江苏 南京 210016)

0 引言

三周期极小曲面(triply periodic minimal surfaces,TPMS)是一种基于数学模型表达的隐式曲面,具有三维周期性、零曲率、几何形状多样等特点[1]。基于TPMS设计的多孔结构相较于传统点阵结构(如体心立方结构)具有高表面积与体积比、表面光滑、孔隙连通性优越、孔隙特征可控等优点[2],在医学植入物、结构轻量化设计等领域得到广泛应用。

在多孔结构实际应用场景中,多孔结构往往需要满足一定的强度要求,Gibson-Ashby 模型是评估多孔结构力学性能最为经典的模型。Gibson-Ashby模型表达了多孔结构孔隙率与力学性能之间的关系[3],但是除了孔隙率这一影响多孔结构力学性能的主要因素外,孔隙形状、尺寸及空间分布也会对其力学性能产生影响[4],而且由于多孔结构具有复杂的结构特征,其成形实体与设计模型之间往往存在较大误差[5],在多孔结构的设计阶段难以准确地评估其真实孔隙率,因此采用Gibson-Ashby 模型预估的力学性能与实际值相差较大,如吴先哲等[6]采用Gibson-Ashby 模型预测的多孔结构弹性模量与实际值相差高达96%;张国庆等[7]采用Gibson-Ashby 模型预测的正八面体结构的力学性能与实际值相差高达68.3%。为了解决这一问题,国内外研究人员对Gibson-Ashby 模型进行了修正。JHA等[8]根据多孔结构的孔隙特征修正了Gibson-Ashby 模型的系数,并提出了修正后系数的取值规律;阮文超等[9]修正了孔隙率的计算方式,进而完成了对Gibson-Ashby 模型的修正;韩春光[10]分析了开孔泡沫材料的变形机制,对Gibson-Ashby 模型进行了推广;HU等[11]通过分析结构的宏观特征,引入有效相对密度这一概念来修正Gibson-Ashby 模型。

尽管国内外许多研究人员针对Gibson-Ashby 模型做了一定的修正,但是这些研究主要是通过进行大量的试验和理论计算,依据多孔结构的孔隙特征修正Gibson-Ashby 模型的系数,修正过程繁琐。此外,由于难以定量地描述多孔结构的结构参数对孔隙特征的影响,因此未能建立多孔结构的结构参数与力学性能之间的关系模型,在设计多孔结构时不能直观地预估其力学性能。针对在多孔结构设计阶段难以直接预测其力学性能的问题,本文以TPMS模型中的Schwarz_P结构为研究对象,采用选区激光熔化(selective laser melting,SLM)技术制备了不同结构参数的Schwarz_P结构,进行了压缩试验,研究了其力学性能,建立了力学性能与结构参数之间的关系模型。

1 试验方法、材料及设备

1.1 Schwarz_P结构

本文以TPMS模型中的Schwarz_P曲面为研究对象,Schwarz_P曲面方程φΡ(x,y,z)如式(1)所示。

(1)

式中:k为单元大小;c为形状因子。

图1为不同结构参数的Schwarz_P结构的图像。由图1可知,改变单元大小k值, Schwarz_P元胞单元大小随之改变,Schwarz_P结构的孔隙大小发生改变;改变形状因子c值,Schwarz_P曲面偏移值随之改变,Schwarz_P结构的形状进而发生变化。因此通过调控单元大小和形状因子的取值可实现对Schwarz_P结构孔隙特征的精确化控制。

图1 Schwarz_P结构图像

需要指出的是,形状因子c存在阈值,即当c达到一定值时,Schwarz_P结构上下层连接线过细,产生夹断现象,夹断现象的产生导致Schwarz_P结构不连续,因此需要对形状因子的取值做出限制。张明康[12]对Schwarz_P结构的夹断行为做了一定研究,研究结果表明当形状因子c为1时,Schwarz_P结构会出现夹断现象,因此形状因子c最大值应小于1。

1.2 基于加工轨迹构造的多孔结构设计方法

本文采用基于加工轨迹构造的多孔结构设计方法完成Schwarz_P结构的设计,该设计方法相较于多孔结构传统设计方法的显著区别是无需构建多孔结构的CAD模型,仅仅需要构建为多孔结构的设计提供空间尺寸约束的壳体模型,通过隐式函数方程或者自然规则来完成多孔结构的隐式表达,依据隐式表达构造多孔结构加工轨迹,最后生成打印文件[13]。Schwarz_P结构设计的主要流程如下:1)对壳体模型切片,在切片得到的二维轮廓内生成点阵区域,将点阵区域划分为二维轮廓内部点、边界点和外部点,舍弃外部点,保留内部点和边界点;2)依据Schwarz_P曲面方程生成元胞单元轨迹;3)将点阵与元胞单元轨迹求交,边界点和内部点与元胞单元轨迹的求交结果分别为Schwarz_P结构的边界轨迹和内部轨迹;4)合并边界轨迹和内部轨迹,完成一层Schwarz_P结构的轨迹构造;5)重复上述步骤,完成所有二维轮廓的轨迹构造,生成打印文件,即完成Schwarz_P结构的设计。

1.3 试验设计

本文以Schwarz_P结构的单元大小k和形状因子c为因素,设计两因素五水平的全因子试验,Schwarz_P结构的三维尺寸为(10×10×20)mm3,并采用SLM技术制备,全因子试验参数设置如表1所示。为了保证试验结果的准确性,每组结构参数制造3个样品。在制备不同结构参数的Schwarz_P结构时,SLM工艺参数保持一致,SLM工艺参数如表2所示。

表1 全因子试验参数设置

表2 SLM工艺参数

1.4 试验材料及设备

Schwarz_P结构成形试验选用的粉末是某公司生产的Ti6Al4V粉末,成形设备为某公司研发的Ti150打印机。本文参照《GB/T7314—2017金属材料室温压缩试验方法》和《GB/T1453—2005夹层结构或芯子平压性能试验方法》[14-15],在室温下采用cmt505电子万能试验机进行压缩试验,同一组结构参数的Schwarz_P结构进行3次压缩试验,试验机载荷加载速度为2mm/min,载荷加载方向与Schwarz_P结构成形方向一致。

2 试验结果与分析

2.1 试验结果

图2为本文制备的Schwarz_P结构样品。由图2可知,本文制备的Schwarz_P结构表面无宏观缺陷,成形效果良好。图3为Schwarz_P结构的应力-应变曲线(本刊黑白印刷,相关疑问咨询作者)。由图3可知,Schwarz_P结构的应力-应变曲线呈现周期性上升和下降的现象,这是由于Schwarz_P结构具有周期性,在压缩过程中多孔单元逐层被压溃,因此其应力-应变曲线为周期性上升和下降的曲线。

图2 Schwarz_P结构样品

图3 Schwarz_P结构应力-应变曲线

本文对Schwarz_P结构弹性变形阶段的应力-应变曲线进行线性拟合,以拟合直线的斜率作为Schwarz_P结构的弹性模量,以应力-应变曲线中的应力峰值作为Schwarz_P结构的抗压强度,Schwarz_P结构的力学性能如图4所示。本文取3次压缩试验得到的弹性模量和抗压强度的平均值作为Schwarz_P结构的等效弹性模量和抗压强度,如图5所示。由图5可知,本文制备的Schwarz_P结构的最大弹性模量为2.175GPa(k=1、c=0.6),最小弹性模量为0.097GPa(k=5、c=0.2),最大抗压强度为101.663MPa(k=1、c=0.6),最小抗压强度为2.442MPa(k=5、c=0.4)。

图4 3次压缩试验得到的力学性能

图5 Schwarz_P结构的等效力学性能

2.2 主因子分析

本文采用Schwarz_P结构的结构参数与力学性能的交互作用图和主效应图来分析其结构参数对力学性能的影响,如图6、图7所示。由图6(a)和图7(a)可知,交互作用图中的直线近乎重合,单元大小k和形状因子c未发生交互作用;由图6(b)和图7(b)可知,弹性模量和抗压强度均随单元大小k的增加而显著减少,形状因子c的变化对弹性模量和抗压强度影响甚微,单元大小k为影响Schwarz_P结构力学性能的主要因素。综合对结构参数与力学性能的交互作用图和主效应图的分析可知,Schwarz_P结构的力学性能由单元大小k决定,与形状因子c无关。

图6 弹性模量因子图

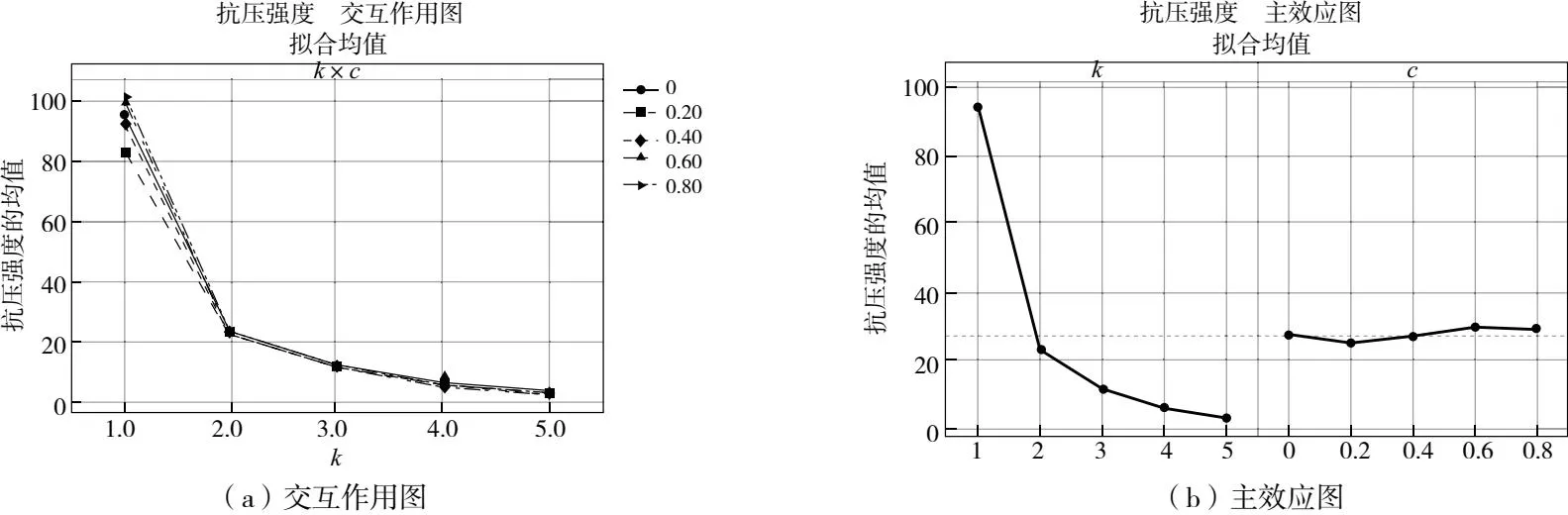
图7 抗压强度因子图

2.3 模型拟合

为了对Schwarz_P结构的力学性能进行直观的预测,结合2.2节关于Schwarz_P结构参数的主因子分析,本文建立变量为单元大小k的统计学模型描述结构参数与力学性能之间的关系,分别如式(2)、式(3)所示。

E=a+b×k+c×k2+d×k3

(2)

σ=e+f×k+g×k2+h×k3

(3)

式中:E为弹性模量;σ为抗压强度;k为单元大小;a、b、c、d、e、f、g、h均为待拟合的常数。拟合结果如图8所示。由图8可知,弹性模量与单元大小k之间的关系模型的拟合优度R2为0.996 86,抗压强度与单元大小k之间的关系模型的拟合优度R2为0.988 14,拟合效果良好。此外,由图8可知,存在个别样品(样品结构参数分别为:k=1,c=0.4;k=2,c=0.8)的力学性能明显偏离拟合曲线的情况。这是因为在SLM成形过程中,这些样品表面附着了大量未完全熔化的粉末颗粒[16],因此其力学性能与拟合曲线之间存在较大的偏差。

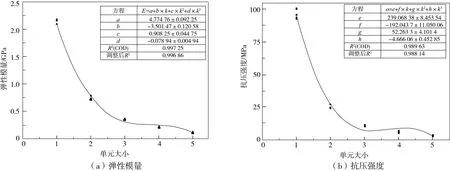
图8 Schwarz_P结构力学性能关系模型拟合结果

2.4 模型验证

为了验证本文建立的关系模型的有效性,本文采用相同的设计方法设计了5组不同于1.3节全因子试验结构参数的Schwarz_P结构,采用SLM技术制备,SLM成形工艺参数与表2相同,并在相同的试验条件下测试其力学性能,与采用本文建立的模型预测的力学性能进行对比,对比结果如图9所示。由图9可知,采用本文建立的模型预测的力学性能与实际力学性能基本保持一致,弹性模量预测值与实际值的最大误差为9.5%,最小误差为3.9%,抗压强度预测值与实际值的最大误差为7.9%,最小误差为4.6%。此外,由于本文建立的关系模型直接描述了Schwarz_P结构的结构参数与力学性能之间的关系,因此该模型可在多孔结构设计阶段直观地预测多孔结构的力学性能,能够为Schwarz_P结构的设计提供指导。

图9 力学性能验证试验对比结果

3 结语

本文选取TPMS模型中的Schwarz_P曲面,采用基于加工轨迹构造的多孔结构设计方法设计了不同结构参数的Schwarz_P结构,利用SLM技术成功制备,通过压缩试验研究了Schwarz_P结构的力学性能,建立了弹性模量和抗压强度与结构参数之间的关系模型,模型拟合优度分别为0.996 86和0.988 14,力学性能验证试验结果表明本文建立的模型能有效预测Schwarz_P结构的力学性能,可在Schwarz_P结构的设计阶段直观地预估其力学性能。