车轮多边形磨耗参数对地铁车辆动力学性能影响分析

杨鹏军,李雪,蒲高,关红艳

(1. 兰州交通大学 机电工程学院,甘肃 兰州 730070; 2. 成都地铁运营有限公司,四川 成都 610066)

0 引言

随着铁道车辆大量运营,多边形车轮磨耗包括地铁车辆在内的许多轨道车辆中都可观测到。翟婉明等[1]指出,在轨道交通预防轮轨侧磨和剥离中,轮轨关系和高负荷轮轨匹配问题仍是首要问题。黄桢国等[2]从测力轮对和加速度传感器分析中发现,影响地铁动车和拖车运行平稳性的因素是速度和载重。王伟等[3]研究轮轨接触发生周期性脱落,提出延缓车轮不圆顺策略是采用柔性轮对和小刚度轨道。李伟等[4]在车辆各零部件研究中发现地铁车轮多边形发生主要是轮对弯曲共振引起,通过加粗轮轴可有效减少多边形发生。PENG等[5]认为,在小半径曲线和牵引力矩大的轨道上轮轨接触黏着振动可激发轮对扭转模态,导致接触参数波动,影响车轮原始磨耗和车辆动力学性能。温士明等[6]研究地铁车轮多边形对浮置板轨道影响,表明多边形磨耗使浮置板轨道减振效果变差。张茉颜等[7]研究地铁小半径曲线车轮多边形对列车安全影响,表明轮重减载率为安全限值评判更符合实际。宋小林等[8]研究地铁线路钢轨波磨对轮对振动加速度影响,提出波深时变率钢轨打磨标准和轮轨力极值。宋志坤等[9]研究了轮轨非均匀磨耗与轮轨力、速度的相近关系,发现钢轨波磨波长和多边形幅值对振动特性影响较大并呈现周期性变化。另外,有建立旋转轮对来分析车轮多边形演化,并有等频可分的规律且来源于轮轨接触振动[10-11]。有砟轨道相比无砟轨道引起车轮多边形磨耗更加剧烈,减缓车轮多边形磨耗可从扣件和阻尼着手[12]。本文通过CAD软件建立车轮、钢轨三维模型,用ABAQUS有限元模型联合SIMPACK建立轮轨柔性某地铁B型车辆刚柔耦合动力学模型,研究多边形不同阶数、谐波幅值对动力学的影响。

1 计算分析理论

1.1 轮轨接触计算模型

在刚柔耦合动力学模型中,轮轨滚动接触主要计算轮轨接触区中法向力和切向力。赫兹理论可确定椭圆接触面形状和接触区半空间压力分布状态,而轮轨接触近似椭圆接触,故用赫兹理论求解轮轨法向力。Kalker理论[13]考虑车轮滚动中的蠕滑和自旋,所提的FASTSIM算法求解速度快,故切向力采用Kalker的FASTSIM算法计算,其中轮轨赫兹接触计算数学模型为

(1)

式中:Fz为接触斑垂向载荷;a为接触斑网格的半长轴;b为接触斑网格的半短轴;x为接触斑单元网格节点横坐标;y为接触斑单元网格节点纵坐标。

1.2 车轮多边形数学模型

针对车轮多边形磨耗,通过输入简谐调和函数对车轮施加不同谐波幅值(以下简称幅值)和阶数来模拟车轮多边形,阶数为车轮转动1圈内波长个数,通常车轮偏心、椭圆化由1阶、2阶多边形引起,当列车速度为v时,引起轮轨系统振动频率为fn,其计算数学公式如下:

(2)

(3)

ΔR(α)=Tsin[n(α+α0)]

(4)

r=R-ΔR

(5)

式中:n为阶次;λn为谐波幅值;α和α0是车轮转动角和初始相位角,rad;ΔR为车轮轮径差、R为车轮名义滚动圆半径、r为车轮实际滚动圆半径,m;T为不圆度波深幅值,m。

1.3 刚柔耦合动力学理论

轨道车辆系统建模分上部、下部、外部,建立轮对、钢轨柔性能更真实地反映轮轨力及动力学性能,故轨道车辆系统动力学方程为

(6)

在无约束情况下车辆刚柔耦合动力学方程为[11]:

(7)

(8)

2 计算分析仿真模型

2.1 刚柔耦合动力学仿真模型

本文为研究车轮多边形磨耗参数对动力学性能的影响,用CAD软件建立LM型车轮和CHN60轨三维模型,车轮材料密度7.85×10-3kg/m3,弹性模量2.1×105MPa,泊松比0.3;钢轨材料密度7.85×10-3kg/m3,弹性模量2.06×105MPa,泊松比0.3。利用ABAQUS建立有限元模型,用Lanczos算法进行模态求解,省略前6阶自由模态,部分结果见表1。

表1 轮、轨缩减前后模态频率对比

表1中,轮、轨缩减前后模态频率变化率最大在4.88%、0.22%以内[14],根据刚柔耦合理论,变化率在10%以内说明子结构模态缩减正确,故该缩减模型可用于计算,且具有较好的准确性。

根据某B型地铁车辆建模参数,利用SIMPACK建立拖车车辆多体动力学模型[15],参数如表2所示。该模型由4个轮对、2个转向架、1个车体、8个轴箱组成。轮对、构架、车体有伸缩、横移、沉浮、侧滚、点头、摇头6个自由度 ,包括牵引拉杆、止挡、减震器等,考虑止挡非线性,模型如图1所示。

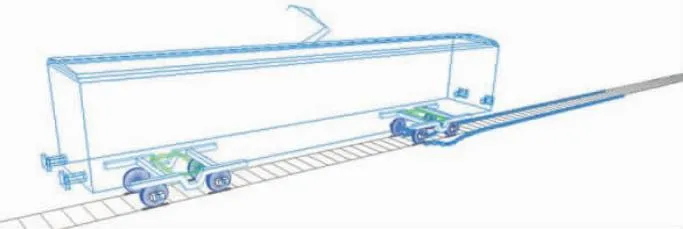
图1 车辆刚柔耦合动力学模型

表2 车辆部分建模参数

2.2 模型的对比与验证

柔性轮对动力学模型主要考虑轮对柔性变形。时域中,让车辆以速度70km/h通过一段理想轨道工况,对比一位轮对右翼车轮轮轨垂向力和纵向蠕滑力。刚性轮轨垂向力与纵向蠕滑力几乎平稳,没有上下波动,柔性轮轨垂向力与纵向蠕滑力有上下波动,轮对旋转引起固有频率增大波动,故用柔性轮对能更精细模拟动力学变化,其对比如图2、图3所示(本刊黑白印刷,相关疑问请咨询作者)。

图2 轮轨垂向力

图3 纵向蠕滑力

验证如下:让车辆以一定速度行驶在包含一段激励和无激励线路上,看轮对横移量是否收敛到0.01mm来判断模型是否达到稳定[15],如图4所示;采用降速法看出刚性轮车辆非线性临界速度较柔性轮小,大致在173km/h之内,而柔性轮车辆非线性临界速度在209km/h内,故说明该车辆模型稳定,可用于计算。

图4 非线性临界速度

3 多边形磨耗参数对车辆动力学影响

3.1 车轮多边形磨耗参数对轮轨垂向力影响

基于柔性轮对车辆刚柔耦合动力学模型和多边形数学模型,不考虑左右车轮相位差,取阶数22阶,幅值0.03mm,分析速度不同情况下仿真有无多边形对轮轨垂向力的影响。如图5所示,随速度增加含多边形会加快轮轨垂向力演化,上下波动较大,无多边形轮轨垂向力增速基本在平稳状态,波动不大。

图5 不同速度下轮轨力时域图

如图6、图7所示,当车辆运行以10km/h速度从50km/h增加到80km/h时,有车轮多边形轮轨垂向力最大值增幅分别为24%、22%、29%;无车轮多边形最大值增幅分别为0.36%、0.12%、0.02%;车轮多边形对应主频从115Hz增加到190Hz,到80km/h时,主频与轮对子结构计算2阶弯曲振动模态相近出现共振,导致轮轨垂向力最大值急剧增大到191kN。与标准规定对比可知[16],最大轮轨垂向力已超过其限值170kN的12%,而轮轨共振引起车轮微弱跳轨,导致轮轨垂向力最小值逐渐减小到18.3kN,故车轮多边形对轮轨垂向力影响极大,这时应注意车轮璇修并降低行驶速度。

图6 不同速度下轮轨力最值图

图7 不同速度下轮轨力PSD图

3.2 车轮多边形磨耗参数对轮对、轴箱振动影响

取随机阶数2、6、10、14、18,幅值0.01～0.04mm,速度80km/h,如图8所示,当幅值固定,轴箱振动加速度随阶数增大而增大,其最大相差21m/s2,到14阶时出现增长峰值,增长速率为53%,幅值0.03mm时,随阶数增大轴箱振动加速度呈先增大后减小趋势;当阶数固定,轴箱振动加速度随幅值增大而增大,其最大相差19.5 m/s2,18阶时随幅值增大轴箱振动加速度呈先减小后猛增趋势。如图9所示,当幅值固定,轮对振动加速度随阶数增大呈先增大后减小趋势,其最大相差4.4 m/s2,到14阶出现增长峰值,增长速率为69%,到18阶略有下降趋势;当阶数固定,轮对振动加速度随幅值增大而增大,其最大相差4.6 m/s2,到14阶时,轮对振动加速度先平缓再剧烈增加后有下降趋势。综上对比,轮对和轴箱振动加速度同在14阶随幅值的变化规律呈现一致性,18阶则波动最大,类似跳跃性激振,故主要振动诱因在14阶和18阶,车轮多边形对轴箱振动加速度影响略大。

图8 轴箱振动加速度RMS图

图9 轮对振动加速度RMS图

3.3 车轮多边形磨耗参数对动力学指标影响

研究车轮多边形对轮轨动力学有极大工程应用价值,根据我国《GB5599—2019机车车辆动力学性能评定及试验鉴定规范》[16]确定脱轨系数安全标准为0.8,轮重减载率在实验速度小于160km/h时限值为0.65。取随机阶数2、6、10、14、18,幅值0.01～0.04mm,速度80km/h,如图10所示,脱轨系数随阶次和幅值的增大呈先平缓后增大,幅值0.01～0.03mm和阶数2～14阶时变为稳定状态,当幅值0.04mm、18阶时脱轨系数快速上升到最大值0.71,但仍小于上述脱轨系数安全限值0.8,阶数和幅值变化对脱轨系数有影响,但不会超过安全范围;轮重减载率在阶数2、6、10阶、幅值0.01～0.04mm时影响小,在阶数14、18阶大幅增长,当阶数18阶、幅值0.03mm和0.04mm时轮重减载率迅速增大分别为0.87、1.00,并超过上述轮重减载率安全限值0.65,故车轮多边形对轮重减载率影响最大。根据国家标准,车辆运行品质评定等级如表3—表4所示[16]。

图10 动力学性能指标图

表3 车辆舒适性指标评定等级

表4 车辆平稳性指标评定等级

如图10所示,阶数2、6、10阶、幅值0.01～0.03mm时,车轮多边形对舒适性影响很小,舒适性值在2.694～2.705之间;18阶、0.03mm时舒适性出现最大值3.087;18阶、0.04mm时又降到2.782。综上全区间舒适性在2.694～3.087之间,与表3评定等级对比,车轮多边形对舒适性整体影响等级为3级(一般舒适)。当阶数和幅值逐渐增大时垂向平稳性基本平稳,总体在1.883～1.887之间,横向平稳性呈略微上升趋势,总体在2.373～2.680之间,在18阶、0.01～0.04mm时横向平稳性出现最大值2.680。综上所述全区间平稳性在1.883～2.680之间,与表4评定等级对比,车轮多边形对平稳性整体影响等级为2级(良好),基本在优向良好过渡。

3.4 车轮多边形磨耗对钢轨位移及振动影响

考虑到车轮多边形磨耗对轨道动力响应,建立柔性轨道计算车轮多边形参数对钢轨位移与振动的影响。为验证结果正确性,通过表2车辆参数,计算车辆在以下速度通过柔性轨道时,前后转向架通过钢轨过程需0.62s并会使钢轨产生凹陷峰值,对比图11峰值区间,车辆运行与钢轨凹陷峰值时间区间基本一致,故提高了以下结果正确性。设车辆速度70km/h,幅值0.03mm,车轮多边形阶数2、6、10、14、18,如图11—图13所示,钢轨垂向动位移随阶数增大呈先增大后减小现象,波形受阶数影响较大,垂向动位移2阶时0.368mm, 10阶达到最大0.423mm,18阶垂向动位移下降到0.397mm,位移出现小峰绕主峰现象,同时,阶数增大钢轨垂向振动加速度从2阶的垂向振动加速度5.613m/s2上升到18阶的23.478m/s2,阶数增大使车轮多边形与钢轨固有模态发生激振,钢轨振动加速度PSD值逐渐增大,故阶数对钢轨垂向动位移和振动加速度均有影响,10阶对钢轨垂向动位移影响最大,18阶对钢轨振动加速度影响最大。设阶数为18,幅值0.01mm、0.02mm、0.03mm、0.04mm,随幅值增大,钢轨垂向动位移变化呈缓慢增长至最大0.408mm,波形受幅值影响较小,同时钢轨振动加速度从0.01mm的8.148m/s2增加到0.04mm的30.935m/s2,由于多边形与柔性轨模态共振,如图13所示,主频周围出现倍频现象。综上,阶数对钢轨垂向动位移影响大于幅值的影响,幅值对钢轨振动加速度影响大于阶数的影响,故阶数、幅值的增大使车轮多边形与钢轨共振激烈,加快了振动速率。

图11 钢轨垂向动位移图

图12 钢轨振动加速度图

图13 振动加速度功率谱密度(PSD)图

4 结语

1)不同速度级下随速度增大含车轮多边形磨耗对轮轨垂向力影响由小增大,由于车轮多边形振动频率与轮对子结构二阶弯曲模态产生共振,在80km/h时轮轨垂向力最大值超过限值170kN的12%,这时要注意璇修车轮,限制轮轨垂向力增长。

2)轮对和轴箱振动特性随阶数和幅值增大、逐渐增大。在14阶随幅值的变化规律呈现一致性,18阶则波动最大,类似跳跃性激振,形成主要振动诱因,车轮多边形对轴箱振动加速度影响略大。

3)随阶数和幅值增加脱轨系数逐渐增加但在安全限值之内,轮重减载率受其影响最大,在18阶增长剧烈超过安全限值0.65,增长速率最高,故可用轮重减载率为评判安全标准。车轮多边形对舒适性整体影响等级为3级(一般舒适),对平稳性整体影响等级为2级,基本在优向良好过渡。

4)车轮多边形磨耗参数中阶数相比幅值对钢轨垂向动位移更有影响,幅值相比阶数对钢轨振动加速度更有影响,当阶数一定,幅值增大时,车轮多边形与钢轨出现明显拍振现象。