声像系统中数字信号滤波器的设计与实现

时静依 李冰石 张硕

63850部队 吉林 白城 137000

引言

现代数字通信技术的发展日新月异，频带逐渐不够用的问题也日益严重，所以要充分利用信道，那么在传输信号前，对信号进行频谱压缩就成为至关重要的环节。

但是，一旦限制信号的带宽，接收机端的误码率就会增加。为了减少误码率，提高频带利用率，我们采用数字信号调制技术，让信号的带宽尽可能匹配信道的带宽。

以前，我们用模拟滤波器实现脉冲整形技术，但模拟滤波器的响应会受到各元器件数值波动的影响，这种波动会因公差范围、温度和老化等一系列的参数来标定，容易出现感应、振荡、杂散等现象，同时它的制作和修改较复杂，而且体积非常大，不便于使用。 与此相比，基带数字成形滤波器便于大规模集成，且具有可靠性高，灵活性高，精度高的优势。

数字滤波器由低通滤波器、加法器、转换器、数字乘法器、加法器和延时单元等组成。数字滤波器的核心功能是对输入的离散信号进行运算处理，主要将输入信号通过低通滤波器，去除信号中的高频分量，信号经过平滑后再用于采样，以达到改变信号频谱带宽的目的，从本质上来说它是完成了信号从输入到输出过程，并进行了特定的运算。数字滤波器由IIR(infinite Impulse Response)和FIR(finite Impulse Response)滤波器两大类构成[1]。FIR滤波器的相位是严格线性的，而且其单位冲击响应h（n）是有限长的、稳定的、能通过快速运算法则实现的，而IIR滤波器没有这方面的优势。所以实际应用起来，FIR滤波器实现信号滤波功能更为广泛。我们通常用窗函数法、频率抽样法、最优等波动法等设计FIR滤波器。

1 滤波器硬件结构设计

1.1 FIR滤波器

在移动通信的实际应用中，升余弦滚降滤波器为应用最普遍的成形滤波器，它的频率分布曲线满足奈奎斯特准则，它对正弦输入信号的稳态输出响应满足升余弦特性：

式中：

滤波器的升余弦特性，就是说将信号进行平滑，这种平滑需要有一定的条件，专业术语称这样的平滑为“滚降”，平滑程度用系数来表示，从公式可以看出，滚降因子越大，信号带宽就越宽，滚降因子越小，信号带宽就越窄。如果滤波器没有任何滚降，我们记录它的截止频率为，当滤波器有滚降时，滚降部分的截止频率为，滚降因子的计算公式为。滚降不特指出来波形的具体的形状，只是指在频谱过渡中，在过渡方面的特征。

升余弦滤波器的响应特性可以通过滚降因子来进行调节，该因子由来表示，。将规律总结如下：

一般情况下，用FIR滤波器，有这几个方面的原因：

IIR数字滤波器的相位非线性，会随着截止频率变化，不好把控，而设计FIR滤波器时，设计的方法是线性的，易获得线性相位响应，硬件上易实现，虽然设计起来较IIR滤波器较复杂，但这有利于保证恒定的延迟，在需要恒定延迟的应用中优势明显。

FIR滤波器没有反馈回路，相对来说比较稳定，稳定性是IIR滤波器设计的难点，但却是FIR滤波器的突出优势。对IIR滤波器而言，它有反馈回路，历史的输出会参与实时的反馈，会出现微弱的寄生振荡。

在使用IIR滤波器过程中，极点有时候会杂散到稳定区域之外，IIR滤波器有经济高效的特点，但在研究图像、视频处理，数据传输等有波形携带信息的系统中，采用FIR滤波器较好[2]。

在实际应用中，需要综合考虑多种方面的因素去选择滤波器，而本论文主要讨论数字基带脉冲的成形滤波，故采用FIR结构的滤波器。

1.2 窗函数法设计FIR滤波器

FIR数字滤波器设计方法的基础就是要求所设计的滤波器频率响应逼近性能指标要求的频率响应，窗函数设计法是FIR数字滤波器设计方法之中最常用的设计方法之一。

傅里叶变换研究了时域和频域的关系，用窗函数设计FIR数字滤波器时，一般由要求的理想滤波器的频率响应，通过傅里叶变换的反变换，导出系统在时域上的信息，即：

按照复卷积公式，在时域上相乘，则频域上是周期卷积关系，即：

用卷积公式将截取的信号片段进行周期延展处理，这样就能进行相关的数学运算，设计的好坏就取决于窗函数的频率特性。

而将无限长的信号截断后，信号的频谱会发生变化，原来能量集中的部分被分散到两个较宽的旁瓣频带中去了，产生频谱能量泄露，所以现实情况中要根据不同的设计要求去选择相应的窗函数。

常用的窗函数有：矩形窗（Rectangle Window）、三角窗(Triangular Window)、汉宁窗（hanning Window）、海明窗（hamming Window）、布莱克曼窗（Blackman Window）、凯塞窗（Kaiser Window）。

实验中不能保证不会有泄露发生，所以需要使用窗函数，可以参考表1的指标来选择窗函数。

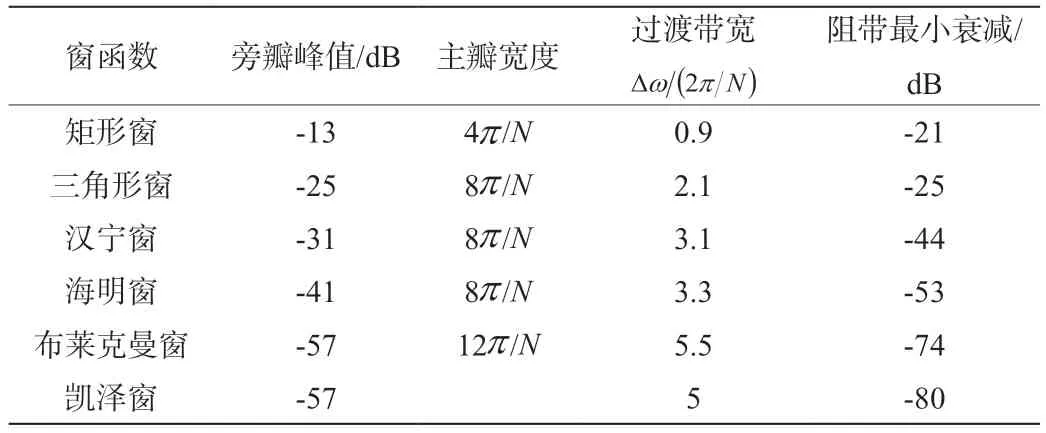
表1 六种窗函数基本参数比较

为避免更多的卷积时的频谱泄露，选择窗函数时要选择尽量窄的主瓣宽度，及较大的旁瓣衰减以更多地压制旁瓣能量。因为频谱分辨率和主瓣宽度是成正比的，与窗长是成反比的，旁瓣衰减和窗长无关。

对于实验中频谱复杂的情况，对频率点的观察要求高，对能量大小的观察要求不高，可选择主瓣宽度非常窄的窗函数，汉宁窗（Hanning Window）可供选择，如果实验中更多地关注幅度响应，则可以选择一个主瓣稍宽的窗函数[3]。

实验中，采样频率为1000Hz，截止频率为200Hz，滚将系数为0.35，滤波器阶数为8，通过FDATool查看各窗函数的幅频响应。由于各窗函数幅频响应图片较多，不再一一展示了，本文中选用的是海明窗（Hamming Window）。

2 仿真与分析

2.1 仿真

本文中所设计的滤波器为8阶升余弦滤波器，采样频率为1000Hz，截止频率为200Hz，滚降系数为0.35，分别进行了直接型结构、直接型对称结构、转置式结构、8倍过采样结构、多相结构的仿真。

2.2 开发环境和工具

本文中成形滤波器的设计使用的是MATLAB软件，利用ISE在FPGA上进行滤波，通过仿真，查看基带脉冲信号成形滤波的传输特性及传输对信号误码率的影响，比较仿真结果，分析仿真中出现的问题，最后得出各种设计结构优缺点的结论，得出各种设计结构实际适合的应用场合。

2.3 分析与心得

综上，虽然各种结构均可达到整形滤波的效果。但是其中多相结构所得波形与其他结构所得波形有所不同，因为唯独它是非对称的。

仿真发现，产生信号混叠的原因是滤波器截止频率与信号源频率之比太小了，当滤波器截止频率小于信号源频率时，就会产生信号混叠的波形，当滤波器截止频率等于信号源频率时，混叠就会逐渐减少，当截止频率大于信号源频率时，混叠会逐渐消失，输出波形边缘也会变得越来越光滑、越来越清晰。不同结构所占用的资源也是不一样的，表2为不同结构滤波器所占用的资源比较：

表2 不同结构滤波器占用资源比较

由上表，对称型结构因为比其他结构少用了一个乘法器，因此占用芯片数最少，同时因为计算量小，需要占用的查找表也就少；而转置式结构的延迟功能在后面执行，因此它的触发器数量多。

3 结论

现实通信中，传输的信号一般是带通信号，即它的中心频带远大于频带宽度，而它的频谱结构基本只取决于等效低通信号的频谱，等效低通信号即本文所说的基带数字信号。基带数字信号的带宽是无限长的，需要限制带宽，研究基带数字信号的成形滤波不仅要研究基本信号的频谱，也要研究脉冲信号间的相关性。

实际仿真实现中发现，信号的发送端用基带成形滤波器，信号的接收端用匹配滤波器，可发挥升余弦滚降信号的最大效用。采用传输系统的传递函数的乘积，并将发射和接收端都设计成平方根升余弦滚降滤波器可降低滤波器的实现难度，因为这样设计能使抽样时的信噪比达到最高，同时能在限制带宽的信道中消除一定的码间串扰。

在声像信号传输中，设计滤波器时，要考虑的因素有提高基带信号传输可靠性和节省带宽。本文讨论了常用的成形函数在现代传输中的频谱特性和各种成形滤波函数的仿真实现，实际实验过程中，还存在一些条件限制，得出的结论也许存在偶然性，有待进一步的研究。