容重器测量结果不确定度评定

龙锋 黄龙飞 韦小华

柳州市计量技术测试研究所 广西 柳州 545006

引言

容重器测量不确定度是指测量结果的不确定性或误差范围，反映的是测量结果的可信程度。虽然目前采用的容重器在测量结果方面能够反映相关情况，但在可靠性方面还有待提升。并且，应用场景的多样化也需要对容重器测量结果的不确定度进行科学评定，以指导相关实践。基于此，探索容重器测量结果不确定度的评定方法，就成为重点内容。

1 容重器测量概述

1.1 测量环境

此次容重器测量的温度为（20±5）℃，室温变化不得大于1℃/h。

1.2 测量标准

此次容重器测量中，二等标准玻璃量器1000mL，A级分度吸量管2mL，F2等级标准砝码10mg～2kg，深度游标卡尺，外径千分尺，内径百分表。

1.3 测量方法

此次测量主要使用两种方法。第一种是采用容量比较法进行检定，这种方法可以准确测量物体的密度或比重，并为容重器的准确性提供参考数据[1]。第二种是采用几何测量法进行检定，这种方法具有适用性广泛、精确性高、不受液体限制、可重复性强等优势。

1.4 被检对象

容重器GHCS-1000型。

2 容重器测量结果评定模型

在此次容重器测量结果评定中，主要选择使用以下模型：

2.1 方差和灵敏系数的确定

首先，根据下面公式得出灵敏系数。

2.2 标准不确定度分量的分析

2.2.1 容量筒容积的不确定度u(V)。

（1）标准玻璃量器引入的不确定度

①误差引入分析。根据相关标准，在假设服从三角分布的情况下，计算出的不确定度：

②变动性引入分析。表1是在重复性条件下10次连续定容测量的结果。

表1 测量结果（单位：mL）

由贝塞尔公式得到标准偏差为：

据此进一步计算出平均值的标准不确定度为：

③温度系数引入分析。在此次研究中，考虑到液体体积膨胀系数远大于玻璃的实际情况，只对水的体积变化进行考虑[3-4]。最终计算出温度系数引入的不确定度为：

根据上述计算结果，这里可以计算出标准玻璃量器引入的不确定度为：

（2）分度吸量管引入的不确定度。

相关标准中明确，在假设服从三角分布的情况下，计算出：

（3）容量筒容积引起的不确定度。

根据上述计算结果，这里可以计算出：

2.2.2 几何法测量容量筒容积不确定度评定。这里计算使用的公式为：

2.2.3 不确定度分量的来源和评定。

①测量重复性引入分析。表2是在重复性条件下对容量筒内径连续10次测量所得出的结果。

表2 测量结果（单位：mm）

根据表2数据，这里可以得出实验标准偏差为：

进而得出：

②内径百分表示值误差引入分析。计算得出：

③内径百分表读数（估读误差）引入分析。计算得出：

④内径百分表调整量块引入分析。根据相关标准可得内径百分表的调整用88.5mm四等量块长度变动量最大允许误差对应测量不确定度为：=0.0004mm。

①输入量引入分析。

深度游标卡尺重复性引入分析。表3是在重复性条件下对容量筒顶部到排气锤高度进行连续10次测量的结果。

表3 测量结果（单位：mm）

结合表3的数据，可以计算出：

深度游标卡尺示值误差引入分析。计算得出：

深度游标卡尺读数(估读误差）引入分析。计算得出：

深度游标卡尺重复性引入分析。表4是在重复性条件下进行10次测量得到的结果。

表4 测量结果（单位：mm）

（3）输入量H3引入分析。

①外径千分尺重复性引入分析。

表5是在重复性条件下对插片厚度连续进行10次测量的结果。

表5 测量结果（单位：mm）

表6 标准不确定度分量汇总表

根据表5测量的结果，可以计算出实验标准偏差=0.015mm，进而计算出

②外径千分尺示值误差引入分析。

③外径千分尺读数(估读误差)引入分析。

（4）合成标准不确定度评定。

①标准不确定度分量汇总。

②合成标准不确定度计算。

2.2.3 容量秤测量引起的不确定度。

表7是在重复性条件下1kg称重量点进行10次试验得到的结果。

表7 测量结果（g）

（2）标准砝码引起的不确定度分量。

对于1kg 测量点，F2等级1kg砝码的最大允许误差MPE为：16mg，则其扩展不确定度为：则其扩展不确定度为：。

（4）容量秤合成标准不确定度。

2.3 标准不确定度一览表

2.3.1 容量比较法标准不确定度一览表（如下表8所示）。

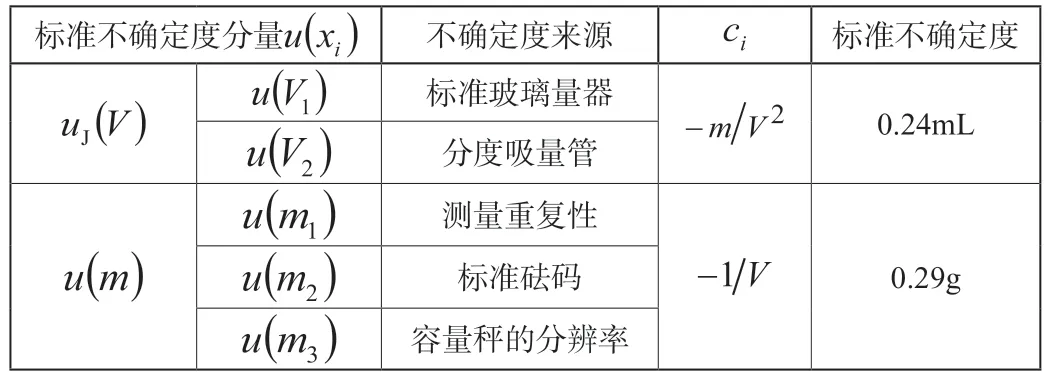
表8 容量比较法标准不确定度一览表

2.3.2 几何测量法标准不确定度一览表，如表9所示。

表9 几何测量法标准不确定度一览表

2.4 容重器的合成标准不确定度

以容积比较法测量容量筒时，容重器的标准不确定度为：

则以几何测量法测量容量筒时，容重器的标准不确定度为：

2.5 扩展不确定度的评定

以容积比较法测量容量筒时，容重器的扩展不确定度为：

以几何测量法测量容量筒时，容重器的扩展不确定度为：

3 结束语

综上所述，文章采用设计的评定模型，对以容积比较法和几何测量法两种方法测量的容重器结果的不确定度进行了评定，得出了相应的结果，这种评定方法为其他相似的容重器测量结果不确定度评定提供了相关内容参考。