具有疫苗接种和标准发生率的ZIKV感染模型

王 霞,李 洁

(信阳师范大学 数学与统计学院, 河南 信阳 464000)

0 引言

寨卡病毒病(ZVD),也被称为寨卡热或简称寨卡,是一种由寨卡病毒(ZIKV)引起的蚊媒疾病,近年来已成为一个新兴的公共卫生问题。寨卡病毒主要通过受感染伊蚊(包括埃及伊蚊和白纹伊蚊)的叮咬传播给人类。此外,寨卡病毒还会通过输血、器官移植和实验室泄漏传播。寨卡病毒病的常见症状包括发烧、皮疹、结膜炎和头痛[1]。尽管目前还没有针对寨卡病毒的正式疫苗,但美国国立卫生研究院(NIH)下属的国家过敏和传染病研究所(NIAID)已于2016年8月初启动了一项疫苗试验,以控制寨卡病毒的传播[2]。值得注意的是,文献[3-4]研究了一些关于寨卡病毒疾病传播及其影响的工作,而这些工作都不包括疫苗接种。有许多方法可以缓解和接种实验性寨卡病毒疫苗,这些疫苗已经在动物身上进行了测试,但在进入市场之前仍在试验中[5-6]。因为疫苗仍处于研发和临床试验阶段,可能不完全有效,即接种者可能会失去疫苗的效力。因此,为了提供一种对所有人都安全有效的疫苗,应该对灭活和减弱寨卡病毒毒性进行更多的实验研究。2021年,SHARMA等[7]提出了一个带有疫苗接种的寨卡病毒感染动力学模型, 采用的是双线性传染率,但当人口数很大时,单位时间内一个染病者所能接触他人的数目是有限的,通常采用标准发生率比双线性发生率更符合实际[8]。

1 模型建立

为了简单描述寨卡病毒传播的基本特征,将总人群分为易感者、接种者、染病者和恢复者;蚊子总群分为易感蚊子、潜伏蚊子、染病蚊子。假设所有的新生儿都是易感的,感染寨卡病毒的蚊子永远无法康复,康复者会被再次感染。因此,考虑如下具有疫苗接种的ZIKV感染动力学模型:

(1)

式中:Sh=Sh(t)、Vh=Vh(t)、Ih=Ih(t)和Rh=Rh(t)分别为t时刻的易感者、接种者、染病者和恢复者的数量;Nh=Sh+Vh+Ih+Rh;Sv=Sv(t)、Ev=Ev(t)和Iv=Iv(t)分别为t时刻的易感蚊子、潜伏蚊子、染病蚊子的数量;Nv=Sv+Ev+Iv;参数λh、μh、δh、λv、μv分别表示人群的出生率、自然死亡率、由疾病诱导的死亡率、蚊子的出生率和自然死亡率;寨卡病毒通过人与人之间的传播速度为βh,通过蚊子与人之间的传播速度为βv;易感者以有效接种率φ接种疫苗;接种者可能会因为接种不完全有效而以η的速度失去疫苗的效力;αh表示人群恢复率;bv表示蚊子叮咬染病者后被感染的速率且潜伏的蚊子以αv的速率变成染病类蚊子;γh表示恢复者丧失免疫力的速率(感染示意图如图1所示)。

模型(1)具有以下初始条件:

Sh(0)>0,Vh(0)>0,Ih(0)≥0,Rh(0)≥0,

Sv(0)>0,Ev(0)≥0,Iv(0)≥0。

由模型(1)可得

容易证明

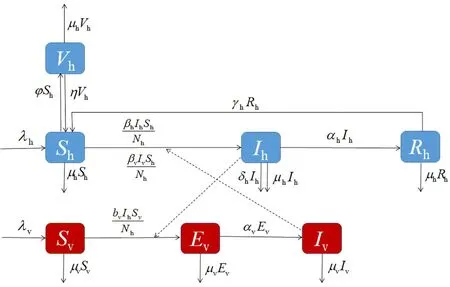
图1 模型(1)的感染示意图

2 基本再生数与平衡点的存在性

记

ρ1=αh+δh+μh,

2.1 模型的基本再生数

为计算模型(1)的基本再生数[10],定义

R0=ρ(FV-1),

式中:

因此,模型(1)的基本再生数为

(2)

式中:

由于无法将Rhh从式(2)表示的R0中分离出来,所以不方便评估性传播和媒介传播的相对贡献。为此定义

式中:R0h=Rhh和R0v=RhvRvh分别表示性传播和媒介传播所对应的基本再生数,即

(3)

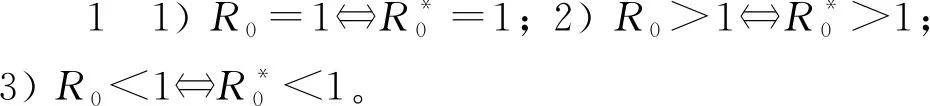
证明1) 由式(2)可得

可得

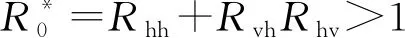
则Rhh>1-RvhRhv。

只需考虑RvhRhv<1,否则

是显然的。由Rhh>1-RvhRhv,可得

当Rhh≥2时,R0<1是不可能的。当Rhh<2时,由RvhRhv<1-Rhh,可得

2.2 地方病平衡点的存在性

除了无病平衡点E0外,当R0>1、δh=0时模型(1)还存在唯一的地方病平衡点E*。设

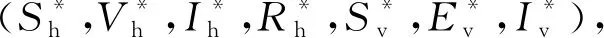
经计算可得到

式中:

k1=αv+μv,

ρ4=αh+μh,

ρ5=βvαvλvbv+βhμvk1ρ6,

式中:

ρ8=βvαvλvbv+βhμvk1ρ7。

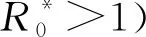
由介值定理可知,F(x)=0至少有一个正根,即模型(1)至少存在一个地方病平衡点[11]。接下来证明模型(1)具有唯一的地方病平衡点。注意到

F′(x)=1+k0+

因此,当R0>1时,模型(1)有唯一地方病平衡点E*。

3 稳定性分析

3.1 无病平衡点的局部稳定性

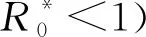
定理2 若R0<1,则模型(1)的无病平衡点E0是局部渐近稳定的;否则,E0是不稳定的。

证明设λ为特征根,则E0处所对应的特征方程为

(λ+μv)(λ+γh+μh)(λ+

μh)(λ+φ+η+μh)Δ(λ)=0,

(4)

式中:

Δ(λ)=(λ+ρ1)(λ+αv+μv)(λ+μv)-

βhρ3(λ+αv+μv)(λ+μv)-αvβvρ2ρ3。

(5)

显然E0的稳定性由Δ(λ)=0的特征根实部的符号决定。Δ(λ)=0可以写成

(λ+ρ1)(λ+αv+μv)(λ+μv)=

βhρ3(λ+αv+μv)(λ+μv)+αvβvρ2ρ3。

(6)

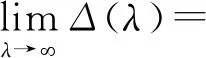
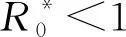
3.2 地方病平衡点的局部稳定性

本节将讨论疫苗效应完全作用和人体永久免疫的理想情况下地方病平衡点的局部稳定性。

定理3 若R0>1且γh=η=0,则模型(1)的地方病平衡点E*是局部渐近稳定的。

证明若γh=η=0,设λ1为特征根,则E*处所对应的特征方程为

(λ1+μv)(λ1+μh)2[(λ1+k1)(λ1+k2)·

(λ1+k3)(λ1+ρ4)-

式中:

k4=φ+μh。

显然E*的稳定性由下式方程特征根实部的符号所决定:

(λ1+k1)(λ1+k2)(λ1+k3)(λ1+ρ4)=

(7)

对于R0>1,只需证明式(7)的所有根都具有负实部。否则,设λ′为式(7)的根且Re(λ′)≥0,通过除以(λ′+k1)(λ′+k2)(λ′+k3)(λ′+ρ4),并对等式两边同时取模可得

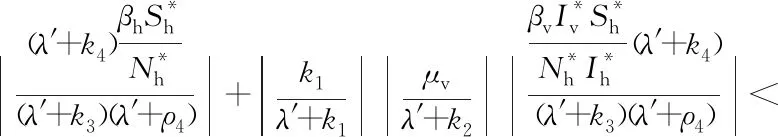
这产生了矛盾。因此,当R0>1、γh=η=0时,E*是局部渐近稳定的。证毕。

4 数值模拟

选取模型(1)的初值:Sh(0)=800,Vh(0)=900,Ih(0)=50,Rh(0)=250,Sv(0)=10 000,Ev(0)=200,Iv(0)=200,Nh=2000;选取参数βh=0.015,βv=0.36,λh=0.1,φ=0.106,η=0.05,γh=0.05,μh=5×10-5,αh=0.3,δh=3×10-4,λv=1000,bv=0.145,μv=0.1,αv=0.1[3,12],可以计算得到R0=1.409 6>1。由定理3可知,模型(1)的解趋向于地方病平衡点E*=(478,1013,72,432,9503,248,249) ,其时间序列如图2所示。

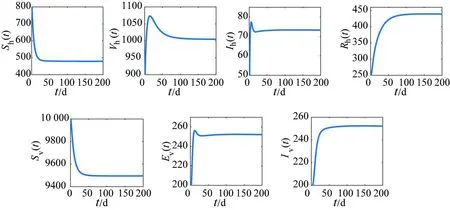
图2 当R0=1.409 6>1时,模型(1)的时间序列图

5 结束语

建立了具有疫苗接种和标准发生率的ZIKV感染模型。该模型包含两种传播方式,即蚊媒传播和性传播。定义了模型的基本再生数R0。分析结果表明:当R0<1时,无病平衡点E0是局部渐近稳定的;当R0>1、疫苗接种完全有效且人体永久免疫时,地方病平衡点E*是局部渐近稳定的。本文的不足之处在于仅考虑疫苗效应完全作用且人体永久免疫的理想情形,一般情形的研究较为困难。此外,使用各种干预措施(使用驱虫蚊帐、避孕套等)控制疾病传播是将来工作的研究方向。