非线性抛物型积分微分方程Galerkin有限元方法超收敛分析

石东洋,张林根

(郑州大学 数学与统计学院, 河南 郑州 450001)

0 引言

抛物型积分微分方程有很强的物理意义,它在具有记忆性质材料的热传导问题、核反应堆中热交换过程、多孔结构黏弹性体的压缩问题、金融数学和期权定价模型、生物学中传染病模型等领域有着广泛的应用。当磁场渗透到物质中时会产生电场,从而产生电流,电流做功导致物质温度升高,进而促使物质的电阻变化。这个过程可用以下的偏微分方程组表示[1]:

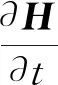
(1)

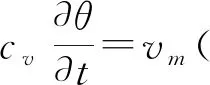
(2)

式中:H=(H1,H2,H3)为磁场强度,θ为温度,cv和cm分别为材料的热容和电导率。当cv和cm与温度θ有关时,方程(1)和(2)可表示为[2]:

(3)

进一步地,若整个物质的温度与空间变量无关,仅与时间变量相关时,则方程(3)可表示为平均积分微分方程[3]:

(4)

式中:|Ω|是区域Ω的体积,t>0。

对于平面磁场H=(0,0,u)的情况,u=u(X,t),X∈R2为标量函数,方程(4)可表示为:

(5)

本文考虑如下的非线性抛物型平均积分微分方程[4-5]:

(6)

u=0,(X,t)∈∂Ω×(0,T],

(7)

u(0)=u0,X∈Ω,

(8)

式中:Ω是R2中边界为∂Ω的有界凸区域,f=f(X,t)和u0=u0(X)是已知函数。

由于非线性系统(6)—(8)存在积分项,往往难以精确求解,故一般使用数值方法计算其近似解。例如:文献[6-7]利用有限差分方法分别研究了磁场H=(0,0,u)和H=(0,u,v)情况下,一维问题数值解的稳定性和收敛性;文献[8]利用线性元研究了一维问题时线性化Backward Euler(BE)有限元格式,推导出了L∞(L2)模的次最优阶误差估计。针对二维问题,其主要工作集中于线性三角形元,文献[4-5]分别研究了它的线性化θ方法和线性化BE格式,仅得出了L∞(L2)模的次最优阶误差估计;文献[9]研究了文献[5]中相同的有限元格式,通过对非线性项的精细估计,得出了L∞(L2)模和L∞(H1)模的最优阶误差估计。文献[10]讨论了最低阶Raviart-Thomas(RT)扩展混合元方法的线性化BE格式,给出了L∞(L2)模的次最优阶误差估计和L∞(H1)模的最优阶误差估计。对于抛物型积分微分方程的研究方法,还可参阅文献[11-13]等。

另一方面,在有限元方法研究中,使用投影算子和插值算子相结合的方法有时会得到更加理想的收敛结果和降低对解的正则性要求。特别是对非线性Schrödinger方程的各向异性三角形线性元半离散格式,单独使用投影算子时无法判断其各向异性特征,到目前为止尚无法构造其插值后处理算子;而单独使用插值算子时甚至无法得到收敛性结果。为解决这一困难,文献[14]提出了将上述两者相结合的方法,在降低对解的时间导数的光滑度的前提下,得到了L∞(H1)模超收敛误差估计。之后引发了一系列有关双线性元的研究工作。例如:文献[15]利用该元研究了线性Schrödinger方程CN格式,导出了L∞(H1)模超收敛结果;文献[16-17]分别利用该元研究了非线性Schrödinger方程线性化BE和CN格式,获得了无网格比约束的L∞(H1)模超收敛结果;文献[18]利用该元研究了非线性四阶Rosenau方程CN格式的混合元方法,获得了无网格比约束的L∞(H1)模超收敛结果;文献[19-20]利用该元分别研究了半线性抛物方程BE格式和非线性双曲方程一个二阶格式的二重网格方法,推出了L∞(H1)模超收敛结果;文献[21-22]分别利用该元和文献[14]中的三角形线性元研究了时间分数阶扩散方程,推出了L∞(H1)模超收敛结果。

本文的主要目的是研究方程(6)—(8)的双线性元CN-Galerkin全离散格式,并借助于插值与投影相结合的思想,再利用插值后处理技术,推导出L∞(H1)模意义下的超收敛结果。

1 全离散格式及超收敛分析

(∇(u-Ihu),∇vh)=O(h2)‖u‖3‖∇vh‖0。

(9)

(∇(u-Rhu),∇vh)=0。

(10)

‖Rhu-u‖0+h‖∇(Rhu-u)‖0≤Ch2‖u‖2。

(11)

‖∇(Rhu-Ihu)‖0≤Ch2‖u‖3。

(12)

设{tn:tn=nτ;0≤n≤N}是[0,T]的一个均匀划分,时间步长为τ=T/N。对于函数序列σn=σ(X,tn),记

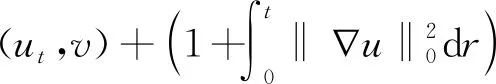
(13)

u(X,0)=u0,X∈Ω。

(14)

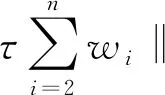
(15)

(16)

(17)

为了方便起见,引入下面的记号:

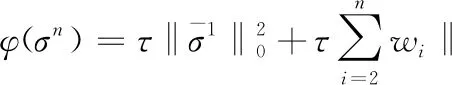
(n=1,…,N),

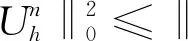
(18)

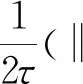
两边同时乘以2τ,将n换成i,并将i从2到n求和,可得

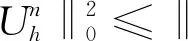
(19)

(20)

结合式(19)和(20)即得式(18)。证毕。

(21)

式中:C是与n、h、τ无关的正常数。

证明由方程(6)和(16),有如下的误差方程:

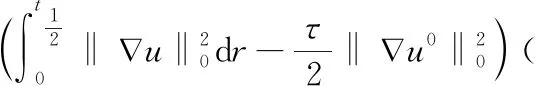
(22)

在式(22)中取vh=η1,0,可得

(23)

下面对式(23)右端逐项进行估计。显然

|A1(η1,0)|≤Cτ2‖uttt‖0,∞‖η1,0‖0≤

|A2(η1,0)|≤Ch2‖ut‖2,∞‖η1,0‖0≤

|A5(η1,0)|≤Cτ2‖∇utt‖0,∞‖η1,0‖0≤

由于

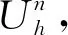
(∇un,∇(un-Rhun))+

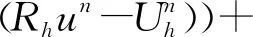
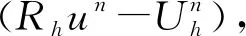
(∇(un-Rhun),∇(un-Rhun))+

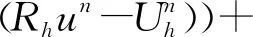
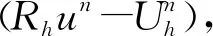
可知

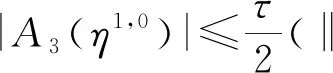
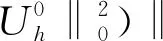
利用文献[25]中截断误差的估计,可得

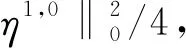
所以式(23)可估计为

(24)

另外,由方程(6)和(17),有如下的误差方程:

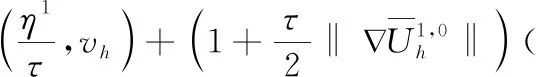
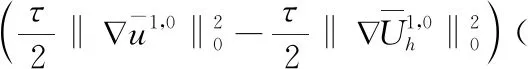
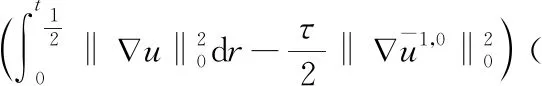
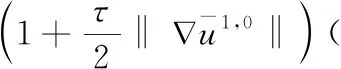
(25)

在式(25)中取vh=η1,可得

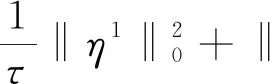
(26)

类似于Ai(η1,0),对式(26)右端各项进行估计,并利用式(24)即得

(27)

另一方面,由方程(6)和(15),可得如下的误差方程:

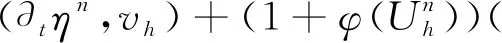
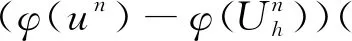
(28)

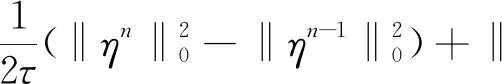
(29)

对式(29)中右端各项进行估计:

再利用式(18),有

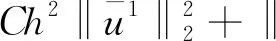
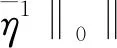
故有

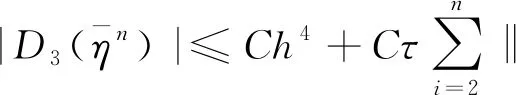
利用数值积分的截断误差的估计有

将以上误差估计代入式(29)即得

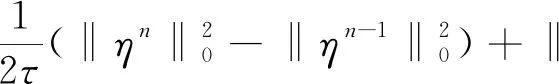
将n换成i,将i从2到n求和,有

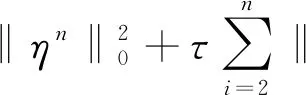
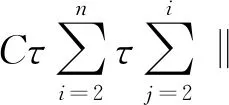
由离散的Gronwall不等式和式(27),可得

(30)

接下来,在式(28)中取vh=∂tηn,有

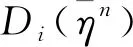
利用式(27)和(30)有

类似地,有

综合上述误差估计,可得

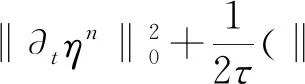
将n换成i,将i从2到n求和有

(31)

从而利用式(27)有

‖∇ηn‖0≤C(h2+τ2)。

利用三角形不等式和式(12),可得

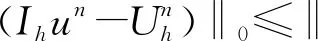
‖∇(Ihun-Rhun)‖0≤C(h2+τ2)。

证毕。

2 数值算例

考虑方程(6)—(8),其中Ω=(0,1)×(0,1),u=e-tsin(πx)sin(πy),由此可以唯一确定f(X,t)。计算中,对每个方向上采用m+1个节点的均匀剖分,并用双线性元进行求解。

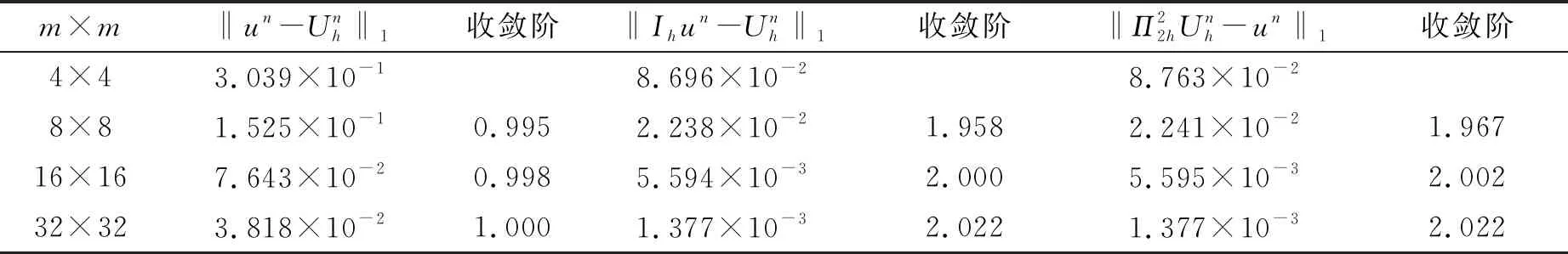
表1 当t=0.5, τ=h时误差结果

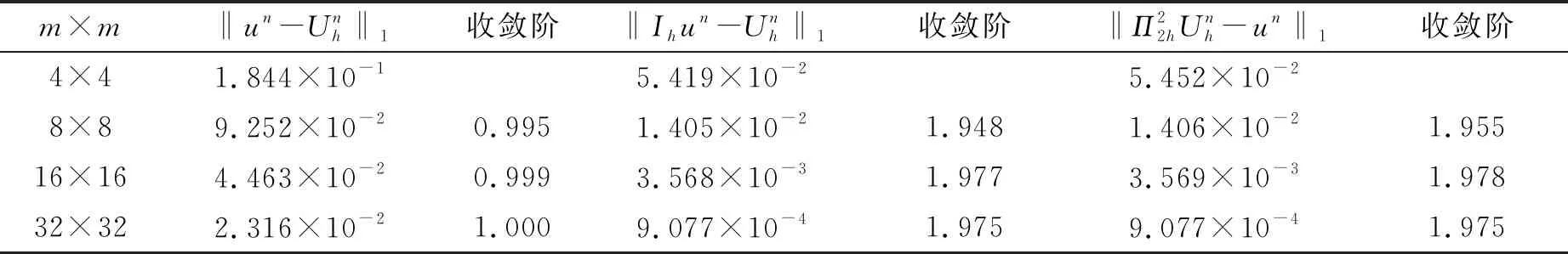
表2 当t=1, τ=h时误差结果

3 结束语

针对二维磁场中所出现的非线性抛物型积分微分方程,利用协调双线性元提出了一种CN格式的Galerkin有限元方法。借助于该元的高精度结果,并采用插值与投影相结合和插值后处理技术,导出了L∞(H1)模的超逼近和超收敛估计。同时通过数值例子验证了理论分析的正确性和方法的有效性。该结果改进和完善了以往文献中只有次最优或者最优误差估计的结论。关于此问题的其他有限元方法诸如混合元方法、H1-Galerkin方法、二阶的BDF2格式等其他逼近格式、非协调元方法的应用等,将在以后的研究中予以进一步的讨论。