基于椭球面共形相控阵的卫星可见性仿真分析

史鹏程，吴海洲，孔永飞，武昭希

(中国电子科技集团公司 第54研究所，石家庄 050081)

0 引言

近年来，全球在轨航天器数量急剧增加。国外大规模星座系统“星链”[1]“亚马逊Kuiper”[2]等项目的建设与国内“鸿雁”“虹云”[3]等卫星星座计划的实施向多目标卫星可见性提出了更高的测控需求[4]。面对庞大的卫星系统，通过全空域波束覆盖技术的进一步提升来实现高效的测控管理已经成为当前航空航天事业发展的必然趋势。

高效的测控管理取决于地面站与卫星的交互。当卫星保持对地面站可见时才能有效地调度任务数据、遥测数据和相关命令[5]。随着近年来卫星数量的不断增加，以单星单站、多星多站分时测控为主的航天测控设备[6]已经难以解决多颗卫星飞越地面站时可能导致的可见性冲突。因此，优化地面站选址，决定卫星何时给定地面站可见，能很大程度在控制设备数量和降低使用成本的前提下解决这一问题，实现全空域内同时多目标的测控和地面站测控管理能力的提升。

就技术层面而言，当前技术途径中传统抛物面天线与平面相控阵天线的测控系统均存在无法突破全空域内同时多目标测控的技术难题，而球面相控阵天线能够实现这一目标[7]。国外早在2005年就已经开始对网格球顶相控阵天线(GDPAA，geodesic dome phased array antenna)在卫星领域的应用进行了讨论[8]，国内于2013年也展开了对于全空域同时多波束测控技术[9]的研究。国内外研究表明，通过球面相控阵天线实现对地基多目标测控管理能力的优化，发展全空域多目标同时测控系统很有必要[10-12]。

本文是基于多目标共形相控阵测控技术展开的重点讨论。主要选用椭球体内接子阵作为地面站数学模型，通过Matlab软件调度，利用当前已经成熟的卫星工具包(STK，satellite tool kit)进行联合仿真分析，以此讨论地面站选址与中国现役卫星之间的可见性关系。在STK/Matlab联合仿真中，设计分段式算法并应用早期终止循环策略，对算法进行优化，以此来处理庞大的卫星轨道数据。同时针对全国范围内的地面站测控工作，形成历史数据方法，为后续相控阵阵列天线最大化利用提供数据基础与应用支持。

1 地面站仿真建模与目标库建立

GDPAA技术被广泛应用于各种军事和科学任务中，采用这种技术建成的天线站通过大量的平面子阵拼接而成，能够提供高效率、宽视角和灵活的波束扫描能力[13]。本文基于GDPAA技术及现有地面测控站数学结构，提出了一种符合实际工程需求的半椭球面共形相控阵阵列地面站模型。

1.1 地面站建模

本文选用椭球体内接子阵作为相控阵数学模型进行探讨。设计椭球的长轴为5.1 m，短轴为4.9 m，短轴所在平面为地球表面，呈圆形。设置内接子阵为0.78 m的正方形，每个子阵的阵元数量为3×3，子阵之间的间隔为0.1 m。根据椭球的几何架构使整体保持椭球面而局部子阵呈平面，使得正方形子阵的四个顶点均内接于半椭球体内。该模型中共有188个小子阵面，分为9层，表1中列出了每层中子阵的个数，每个子阵所在层号用K表示，该层的子阵总个数用M表示。

表1 相控阵布阵层号及每层子阵个数

这种将子阵内接于椭球面形成相控阵的建模方式，对比共形阵，从实际工程角度更容易实现，加工成本低且可以实现模块化[14]。而对于通过少数几个平面阵拼接形成的阵列而言，椭球内子阵的均匀分布保证了阵列在全空域范围内的增益平滑性，并且子阵的间距有效抑制了副瓣和栅瓣。其模型仿真结果如图1所示。

图1 椭球面共形相控阵

1.2 目标库建立

本文所导入数据皆为卫星两行轨道数据。卫星星历，又称为两行轨道数据(TLE，two-line orbital element)，是由北美航空航天防御司令部(NORAD，north American aerospace defense command)开发的一种用于传输卫星轨道根数的数据格式[15]。其以开普勒定律的6个轨道参数之间的数学关系确定飞行体的时间、坐标、方位、速度等各项参数，具有极高的精度。卫星、航天器或飞行体一旦进入太空，即被列入NORAD卫星星历编号目录。列入NORAD卫星星历编号目录的太空飞行体将被终生跟踪。

卫星星历能精确计算、预测、描绘、跟踪卫星、飞行体的时间、位置、速度等运行状态；能表达天体、卫星、航天器、导弹、太空垃圾等飞行体的精确参数；能将飞行体置于三维的空间；用时间立体描绘天体的过去、现在和将来[16]。卫星星历的时间按世界标准时间(UTC，universal time coordinated)计算，并定时更新。

下面以近期发射卫星“风云三F”为例，对于TLE两行数据进行解读。风云三F(FY-3F)气象卫星是2023年8月3日11时47分在酒泉卫星发射中心搭载长征四号丙运载火箭发射升空。其TLE数据如表2所示，两行轨道参数各项参数的意义如表3所示。

表2 卫星FY-3F两行轨道参数

表3 卫星FY-3F 两行轨道参数意义

2 卫星可见性分析

2.1 基于卫星两行轨道报的轨道推算

NORAD将空间目标分为近地周期和深空周期两类，其中近地周期小于225分钟，而深空周期不小于225分钟[17]。根据不同的周期，可以在卫星工具包中设定相应的轨道模型。由于常规的相控阵天线探测不到深空目标，因此本文选用SGP4模型。SGP4采用的主要摄动模型包括地球非球形引力摄动、大气模型摄动和日月引力摄动的一阶项。利用SGP4模型推算卫星目标位置和速度的方法流程如图2所示。

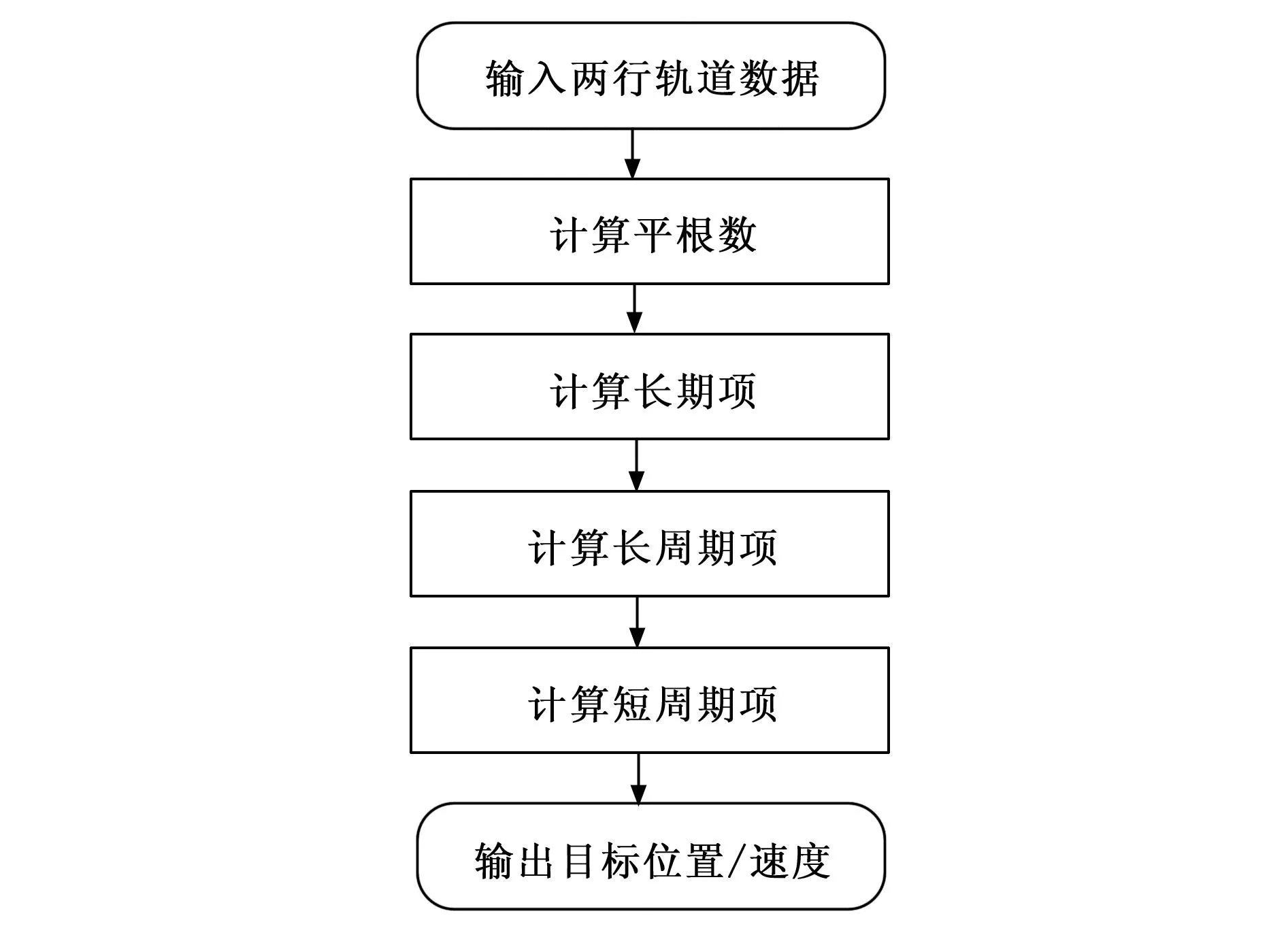
图2 SGP4模型推算卫星轨迹流程图

2.2 坐标系定义

在本文地面站选址与卫星可见性仿真分析中，采用的坐标系主要包括五种，分别是真赤道平春分点坐标系、地心惯性坐标系、地心地固坐标系、地平坐标系与子阵视线坐标系。

真赤道平春分点坐标系(TEME，true equator mean equinox)OE-xEyEzE是一种天球坐标系，其原点位于地球的质心，xE轴指向真春分点，zE轴指向真北天极，yE轴垂直于xE轴和zE轴，组成一个右手直角坐标系。由于春分点和北天极的位置会随着时间而改变，因此在这个坐标系中xE轴的指向是变化的。真春分点指的是考虑了岁差和章动影响后，春分点在真天球坐标系中的位置。

地心惯性坐标系(ECI，earth-centered inertial frame)OI-xIyIzI是在一个惯性空间中，相对于一个“固定的”恒星来说是不动的。ECI坐标系为直角坐标系，坐标系原点处在地球中心处，xI轴为在赤道平面与黄道面的交线，指向春分点，zI轴垂直于赤道平面指向北极。yI轴与xI轴，zI轴构成右手笛卡尔坐标系[18]。

地心地固坐标系(ECEF，earth-centered-earth-fixed frame)OF-xFyFzF随地球同步旋转，是一个相对于地球固定的坐标系。ECEF坐标系为直角坐标系，坐标原点处在地球中心处，xF轴在赤道平面内指向格林威治天文台所在的子午线，zF轴垂直于赤道平面指向北极。yF轴与xF轴，zF轴构成右手笛卡尔坐标系。地心惯性坐标系与地心地固坐标系关系如图3所示，其原点都为地心[19]。

图3 ECI与ECEF坐标系

椭球面共形相控阵地平坐标系OH-xHyHzH以相控阵底部圆形的圆心为原点，基本面为坐标原点处的大地水平面，xH为基本面内由原点指向南为正，yH轴指向东，zH轴垂直于基本面，xH轴与yH轴，zH轴构成右手笛卡尔坐标系。在本篇论文中，定义仰角EH为目标在地平坐标系中的位置矢量和基本面的夹角，方位角AH为-xH方向与目标位置矢量在基本面上投影线之间顺时针方向的夹角，地平坐标系如图4所示。

图4 地平坐标系

子阵视线坐标系是用来定义子阵中各个阵元的具体位置信息以及波束指向相对于子阵的方向信息。该坐标系原点位于子阵的中心，基本面为子阵平面，zv轴与子阵法线方向重合，xv、yv轴位于子阵平面内，xv轴位于椭球面与其过Ov剖线的交线的切线方向，yv轴位于椭球面与其过Ov横截面的交线的切线方向，三个坐标轴符合右手定则，如图5所示。

图5 子阵视线坐标系

2.3 坐标转换及可见性判定

依据2.1中推算出来的位置序列值，进行坐标转换。卫星与椭球面共形相控阵地面站的初步坐标转换将通过卫星两行轨道数据导入，利用真赤道平春分点坐标系、地心惯性坐标系和地心地固坐标系进行。与椭球面共形相控阵天线单元位置及波束形成关系比较密切的坐标系为地平坐标系和子阵视线坐标系，其中椭球面共形相控阵使用的整体坐标系为地平坐标系，相对子阵的位置关系使用的局部坐标系为子阵视线坐标系。

下面对各个坐标的定义如下：(xE，yE，zE)为目标的真赤道平春分点直角坐标；(xI，yI，zI)为目标的地心惯性直角坐标；(xF，yF，zF)为目标的地心地固直角坐标；(xH，yH，zH)为目标的地平直角坐标；(xV，yV，zV)为目标的子阵视线直角坐标；(R，AV，EV)为目标的子阵视线极坐标。

由轨道卫星两行报推算出的结果是真赤道平春分点坐标系下的位置，转换到椭球面共形相控阵子阵极坐标并进行可见性判定需要如下6个步骤：

1)真赤道平春分点坐标与地心惯性坐标的转换：

(1)

Rx(εA)Rz(-ZA)Ry(-θA)Rz(-ξA)

(2)

其中：Δψ为黄经章动 ，ε为黄赤交角，εA为平黄赤交角，Δε为交角章动，ZA、θA、ξA岁差参数，矩阵Rx(θ)、Ry(θ)、Rz(θ)分别为绕x，y，z坐标轴按右手系旋转θ角。

2)地心惯性坐标与地心地固坐标的转换：

假定在初始时刻两个坐标系是重合的，从初始时刻经过t时间后，x轴间的夹角是ω*t，其中ω=7.292×10-5rad/s，为地球自转的平均角速度。两个坐标系间的关系如图所示，地心惯性坐标系绕z轴逆时针旋转ω*t角度即可得到地心地固坐标系，其转换关系为：

(3)

3)地心地固坐标与地平坐标的转换：

(4)

(5)

其中：XG、YG、ZG为椭球面共形相控阵的坐标，λ、ϑ分别为地面站的经度、纬度。

4)地平坐标与子阵视线坐标的转换：

地平坐标系OH-xHyHzH与子阵(N，M)的视线坐标系OV-xVyVzV的对应关系如图4所示。通过椭球面共形相控阵仿真计算出子阵(N，M)的视线坐标系xV轴与水平面zH=0的夹角，定义为θNM，xV轴在水平面投影与xH轴的夹角，定义为φNM。

天线单元在地平坐标系和子阵视线坐标系中的位置存在一一对应关系，这种一一对应关系可以通过坐标旋转和平移进行相互转换，由地平坐标到子阵视线坐标的转换关系如式(6)：

(6)

其中：(x0，y0，z0)为子阵视线坐标系原点OV相对地平坐标系原点OH的平移值。A为坐标旋转矩阵，该矩阵为：

(7)

5)子阵视线直角坐标与子阵视线极坐标的转换：

子阵视线极坐标(R，AV，EV)表示子阵视线坐标系中的具体某位置信息，R表示坐标原点与某位置的距离。子阵视线直角坐标系与子阵视线极坐标系的转换关系如下：

(8)

(9)

(10)

6)椭球面共形相控阵阵面可见性判定：

对于不同空间方位的卫星，参与发射/接收的天线阵元通常不一样。在波束形成中，不参与合成波束的天线单元方向图应置零。本文采用1.1中提出的椭球面共形相控阵作为地面站模型进行可见性分析，其阵面作用判定如下：

综合步骤1)～5)，实现由卫星两行轨道报到子阵视线极坐标的转换，进而得到卫星对应于子阵视线极坐标系下的方位角AV和俯仰角EV。为了使平面子阵达到增益要求，本文设定最大扫描角Emax=60°。当E0≥Emax时，满足扫描角条件的阵元起作用，视为当前子阵对卫星可见，否则阵元增益置零。

3 STK/Matlab联合仿真

卫星工具包是由美国分析图形公司 (AGI，analytical graphic，inc.)开发的航天领域中先进的系统分析软件[20]，STK可以模拟和评估航天系统在真实或模拟环境下的性能，分析复杂的航天、航空、陆地及海洋任务[21]，其应用对象包括卫星、飞机、船舶、车辆、地面站和雷达等。

STK具有强大的功能，能够模拟各领域在任务周期内的全过程。它具有便捷的操作界面，可用于完成任务分析优化等工作，并具有强大的图文输出能力。此外，STK还拥有完善的数据库，可提供恒星、卫星、城市和地面站等数据，并可连接服务器进行在线更新。与此同时，STK还具有可视化功能，可用于提供逼真的二维和三维动态场景以及精确的图表。此外，它还具有良好的实时性和扩展性，可以通过预设的程序接口与Visual Studio和Matlab等软件互联，实现协同开发和优化。因此，STK在航天飞行任务的各个环节中都有广泛的应用，包括系统分析、设计制造、测试发射以及在轨运行等[22-24]。

STK无疑是个非常强大的分析工具，但它自身无法通过编程实现对某些复杂场景的分析，例如循环计算、复杂的迭代嵌套等，导致重复性操作十分花费时间，由此引入STK编程接口。STK编程接口主要由两部分组成：Connect模块接口和COM技术，通过使用STK编程接口，可以进行基于STK引擎的开发。

本文仿真环境搭建基于STK11，MatlabR2016a(64位)，通过STK编程接口实现对STK的调度，在调度时将同时使用Connect命令和COM技术。仿真算法分两个阶段执行：第一阶段，进行仿真环境建立并循环计算各卫星与地面站全天各时段可见性数据，在本阶段仿真中，将椭球面共形相控阵作为一个整体进行仿真；第二阶段，将一阶段所统计可见卫星数据导入椭球面共形相控阵模型中，实现地平坐标系与子阵视线坐标系转换，进而循环判断卫星与各个子阵的可见性关系。

3.1 仿真环境建立与初步筛选

本文截取2023年8月5日卫星两行轨道数据作为原始数据。下面即以2023年8月5日1时-2时漠河古莲机场(北纬52.92°，东经122.43°，海拔40 m)为例，通过STK/Matlab联合仿真的方式搭建场景，根据所采集卫星两行轨道数据建立空间卫星，同时建立以漠河古莲机场为坐标的椭球面共形相控阵地面站，从可见性方面进行仿真分析。进行主要流程说明，第一阶段算法流程如图6所示。

图6 第一阶段仿真流程图

1)STK与Matlab互连，在命令窗口输入“stkInit”出现警告语句如下，即为成功连接。

2)在STK中创建一个场景，命名为Model。设定场景时间，起始时间为5 Aug 2023 01：00：00.00，结束时间为5 Aug 2023 02：00：00.00，仿真时间设为一小时。

3)在STK中建立一个地面站。设定地面站纬度为52.92°，经度为122.43°，海拔为40 m，并同时设置传感器。

4)通过fopen函数读取卫星两行轨道报文件。设定卫星数据时间，起止时间与前文设定相同。

5)利用COM技术获取可见卫星数据，同时判定是否存在可视弧段。

后续循环导入卫星并进行可见性判定，在这里，将地面站模型视为一个整体。通过第一阶段算法对庞大的卫星数据进行初步筛选，将可见卫星数据统计输出。

3.2 可见卫星判定输出

将一阶段所统计可见卫星数据进行坐标系转换，循环导入椭球面共形相控阵模型中，以椭球面共形相控阵阵列为地面测控站模型进行可见性分析，进而循环判断卫星来波是否符合地面测控站模型中子阵的最大扫描角要求，将符合条件的卫星视为可见并进行数据导出。第二阶段算法流程如图7所示。

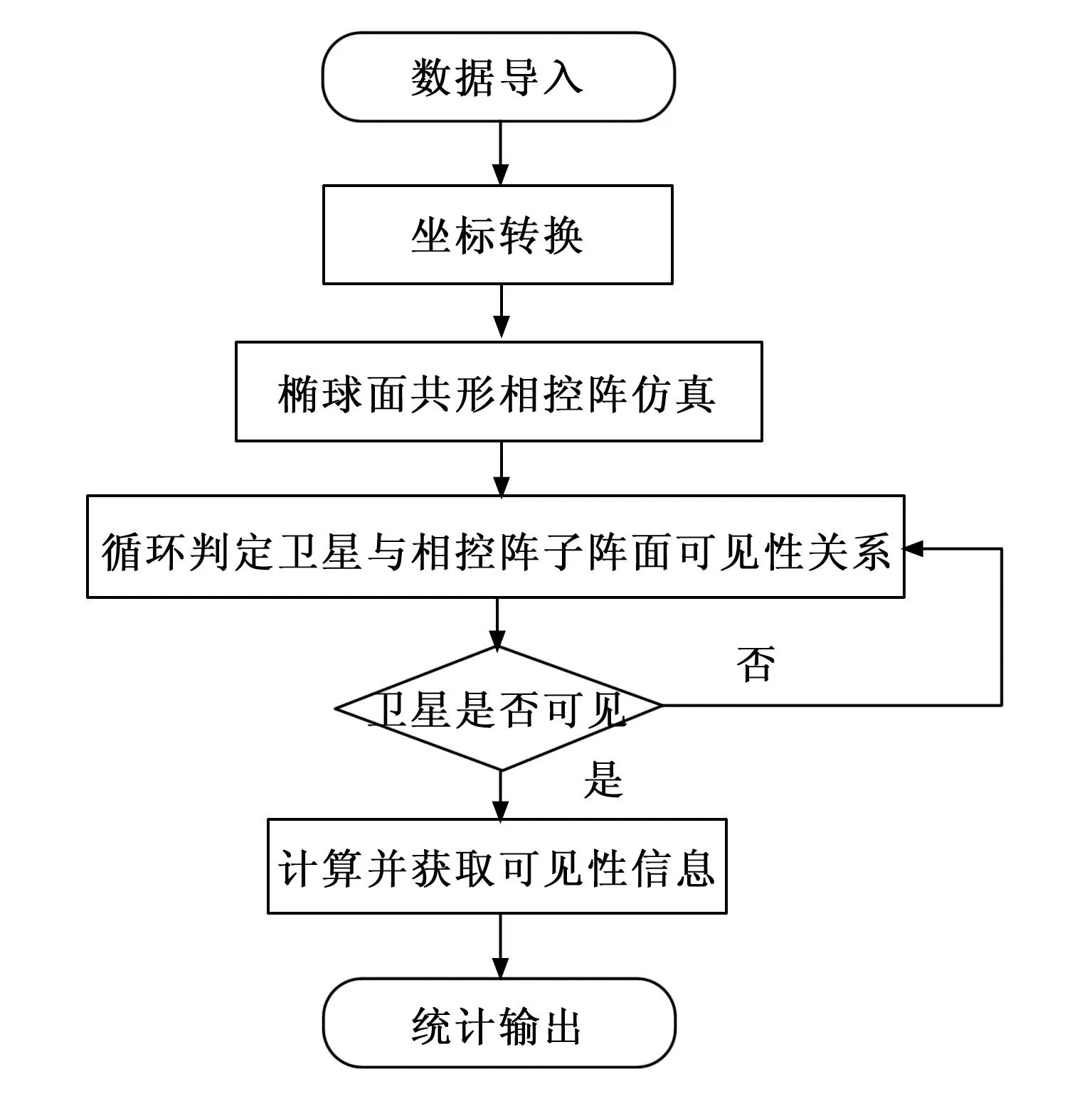
图7 第二阶段仿真流程图

1)数据导入，计算符合条件的卫星数据，为下一步信息提取做准备。

2)通过DataProviders获取卫星第一个可见弧段内的方位角。通过Exec获取场景开始时刻到场景结束的角度数据，设定间隔为60 s。

3)将提取到的卫星数据经过坐标转换导入椭球面共形相控阵的各个子阵面中，循环判定。在此场景中，为了提高算法效率，应用早期终止循环的策略。在可见子阵数量大于等于1时，将作用子阵进行标记，跳出循环并开始下一次迭代。将符合要求的卫星利用access计算提取其可见性的起止时间。

4)在循环结束后，对收集到的数据进行统计并输出。仿真完成，断开STK与Matlab连接。

这种设计方法在第一阶段通过对庞大卫星数据的初步筛选，将大部分无效卫星数据排除在外，将具有可见弧段的卫星导入到第二阶段的仿真中，可以大大减少数据处理的时间，同时也可以提高仿真结果的准确性和可靠性。在第二阶段中，由于只处理具有可见弧段的数据，因此可以让计算资源更加集中在核心的计算部分。应用早期终止循环的策略，从而提高了仿真过程的整体效率，实现算法的优化和性能的提升。

4 仿真实验与结果分析

本文通过上述流程进行STK/Matlab联合仿真，将一天的24个小时划分为24个时间段，每个时间段对应一小时，以此来实现对每个时段卫星可见性的仿真分析。通过每个时段的仿真，可以获取卫星的可见弧段准确时间，为地面站测控资源的最大化利用形成历史数据。

地面站测控站选址如下：首先对于中国国家版图进行概览，中国国家版图呈现雄鸡形状。选取西部喀什机场(北纬39.54°，东经76.02°)，北部漠河古莲机场(北纬52.92°，东经122.43°)，南部三亚站(北纬18.30°，东经109.49°)和中部西安北站(北纬34.38°，东经108.94°)作为四个地面站选址，海拔统一设定为40 m。以此来讨论在海拔统一的情况下，站址的地理位置选择和中国现役卫星之间的可见性关系。所选地面测控站在中国国家版图中的地理位置如图8所示。

图8 地面测控站选址

4.1 单站卫星可见性分析

选取2023年8月5日1时-2时漠河古莲机场仿真结果进行说明。在此次仿真中，该椭球面共形相控阵与卫星的可见数量是最多的，达到205颗。在STK仿真中3D模型为图9。

图9 STK/3D模型

其中有连接线即为地面站的可见卫星，取一小时为时间段，图9中显示卫星在这一时段内的运动轨迹，同时可以获取地面站对卫星的可视弧段数据，以报表的形式展示在STK软件中，截取部分如图10所示。

图10 部分可见弧段数据

myfac为所设定的地面站名称，分析报告即可得出，对于ID为28058卫星，其相对地面站可见的开始时间和结束时间，总可见时长为737.861 s。而28220卫星对地面站在此时段内没有可视弧段，不存在可见性。

椭球面共形相控阵地面站在该时段仿真模型如图11所示，其中黑色子阵即为该时段地面站对卫星可见所用子阵。与图1进行对比，整个共形相控阵的阵元都呈黑色。结果表明，在这个时段内，以漠河古莲机场为地面站选址坐标，其卫星来波包含各个方向，所有的阵元都被利用起来。

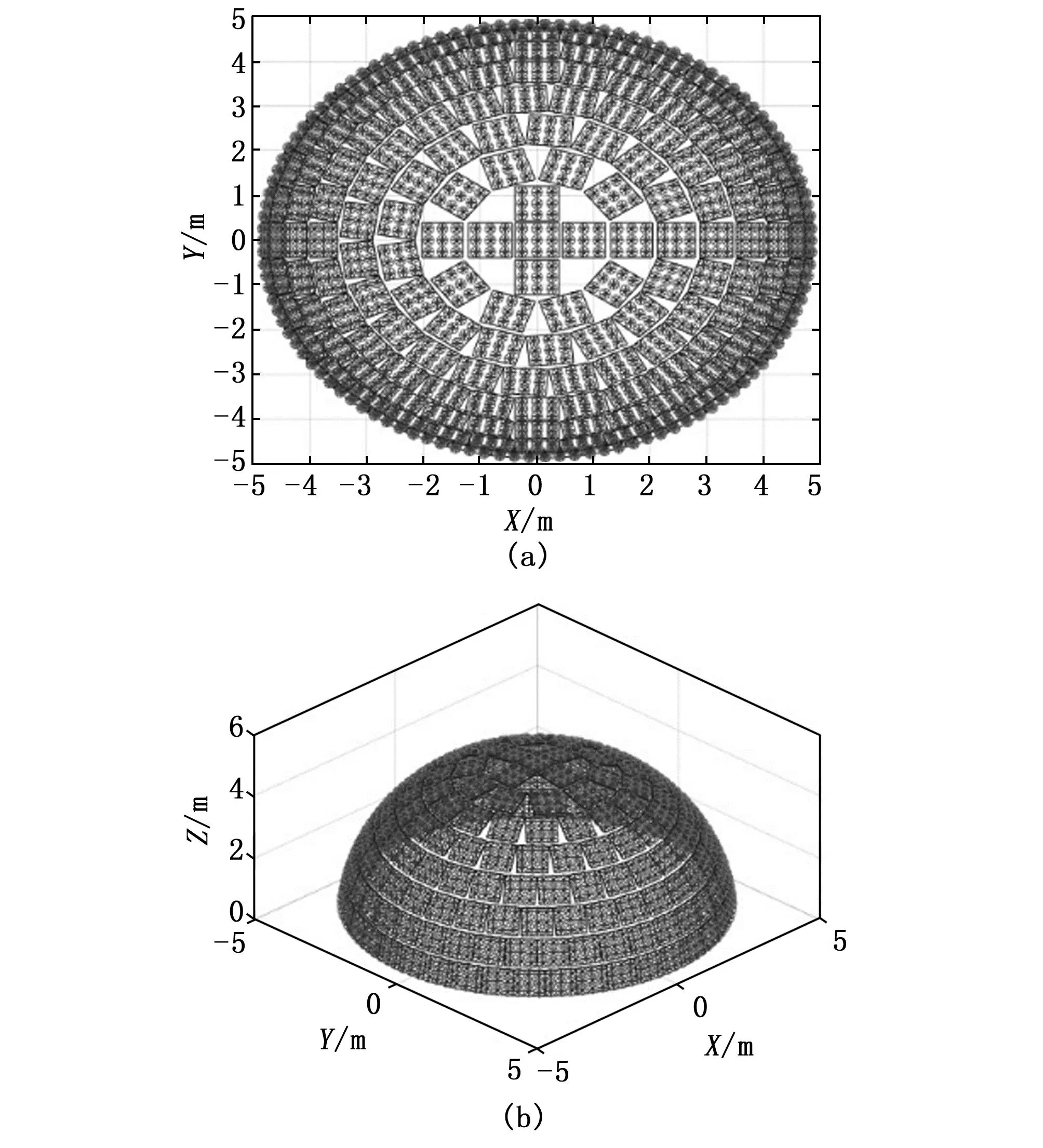
图11 仿真结果图

4.2 四站仿真结果分析

现对整体仿真数据进行分析讨论，以下分别为西部喀什机场，南部三亚站，中部西安北站和北部漠河古莲机场于2023年8月5日，以一小时作为参考时间段的可见卫星数量统计，如图12所示。

图12 四站仿真数据

分析数据，在0点到15点的时间区间内，北部漠河古莲机场地面站对卫星可见数量最多，此期间内存在本次仿真数据最大值，该最大值在1点到2点的时间区间内达到，其可见卫星的数量为205颗。在15点到16点的时间区间内，中部西安北站地面站对卫星可见数量最多，为163颗。在16点到20点的时间区间内，西部喀什机场地面站对卫星可见数量最多，在20点到24点的时间区间内，北部漠河古莲机场地面站对卫星可见数量最大。为了进一步分析，求得全天仿真可见卫星数量平均值并绘制簇状条形图，如图13所示。

图13 可见卫星数量平均值

可知，经度和纬度最大的漠河古莲机场地面站所能观测到的卫星数量最多，每时段平均为171.17颗。而南部三亚站最少，为138.88颗。由此分析在海拔一致的情况下，纬度和经度对地面站与卫星可见性关系。

1)对比中部西安北站和西部喀什机场数据，以西安北站作为基准，喀什机场的纬度为+5.16，经度为-32.92，两地观测卫星数量为+1.34。可以得出结论，纬度对于地面站可见性呈正相关关系，但不能排除经度对于地面站可见性成负相关的可能性。

2)对比南部三亚站和西部喀什机场站数据，以三亚站为基准，喀什机场站的纬度为+21.24，经度为-33.47，两地观测卫星数量为+10.54，

3)对比北部漠河古莲机场和中部西安北站数据，以西安北站为基准，漠河古莲机场的纬度为+18.54，经度为+13.49，两地观测卫星数量为+23.08，综合2可得，经度对于地面站可见性呈正相关关系，排除1中经度于地面站对卫星可见性成负相关的可能性。

综合1)，2)，3)可以得出纬度和经度地面站对卫星的可见性呈正相关关系。然而，这种正相关关系并不是同等强度的。纬度对地面站对卫星可见性的影响较大，而经度的影响相对较小。例如，在中部西安北站与西部喀什机场的比较中，尽管喀什机场的纬度比西安北站高5.16度，但两地观测卫星数量的差距只有1.34颗。而当比较范围扩大到南部三亚站和西部喀什机场站时，尽管喀什机场的纬度比三亚站高21.24度，两地观测卫星数量的差距却达到了10.54颗。

5 结束语

在现阶段仿真中，某地每时刻可见卫星数量较多，原因是仿真中除了地面站选址和子阵最大扫描角的约束外，没有加入任何其它约束，仅考虑在理想情况下地面站选址与卫星的可见性之间的关系。在后续研究过程中，应加入相关约束条件以此来模拟实际工程中的情况，这些约束包含地面站与卫星间最大距离约束、太阳视线角约束和最短观测弧长约束等。

本文提出了一种符合实际工程需求的半椭球面共形相控阵阵列地面站模型，以共形相控阵中子阵作为单元进行卫星可见性仿真分析。在设计大规模卫星可见性分析的STK/Matlab联合仿真算法流程中，处理大量数据和进行复杂计算是关键问题之一。为了解决这个问题，本文采用分段式算法并应用早期终止循环策略，极大地提高了仿真计算效率，从而更好地满足大规模卫星可见性分析的需求。

从可见性方面对地面站选址与中国现役卫星之间的关系进行了分析，结果表明，在海拔统一的情况下，地面站选址的纬度和经度都和卫星可见性成正相关关系，其中，地面站的纬度对于可见性的影响相对较大，而经度于卫星可见性的影响相对较小。同时，仿真结果为全国范围内地面站测控工作积累科学数据，为后续相控阵阵列天线最大化利用提供数据基础与应用支持。