面向DSP平台的CiSSA-CSP特征提取算法的移植与优化

刘哲贤，赵金库，赵玉峰，王 鹏

(1.清华大学 精密仪器系，北京 100084；2.黑龙江北方工具有限公司，黑龙江 牡丹江 157000)

0 引言

脑机接口(BCI，brain computer interfaces)是一种人与外部设备的交互系统，通过信号解析算法，解析人的大脑活动，从而根据人的大脑活动生成相应的控制信号，帮助人类在不通过神经与肌肉的情况下与外界实现交互[1-2]。BCI系统主要由四个部分组成，分别是信号监测、特征提取、控制信号输出和外部设备响应与交互。

从信号监测的手段来看，BCI系统主要分为两类，分别是侵入式与非侵入式。侵入式脑机接口通过外科手术将微电极阵列植入大脑中，而非侵入式则将电极布置在头皮上已检测神经活动。相比于非侵入式，侵入式BCI检测到的信号具有更高的信噪比，可用于病理分析、运动控制等领域；但侵入式BCI也面临成本高、有医疗风险、使用不便等问题，同时侵入式BCI的应用场景主要局限于瘫痪病人的协助，而非侵入式则具有更广阔的应用前景，不仅能用于运动障碍人士的康复治疗也能为健康人带来不一样的生活体验。非侵入式BCI中最常用的检测手段是脑电图(EEG，electroencephalography)[3]。

EEG信号为多通道数据，由紧贴在头皮上的若干个电极采集得到，是记录大脑皮层神经元活动的电生理信号[4]。EEG相比其他检测手段成本更低，便携性更好，但EEG的信号质量是困扰研究人员的问题[5]。由于神经元的电生理信号需穿过颅骨和头皮才能被位于头皮表面的电极检测到，因此EEG信号具有幅值低(微伏量级)、信噪比低、极易受外界干扰、信号存在伪影[6]等特点。

从信号类型来看，脑电信号主要分为自发脑电和诱发脑电。其中诱发脑电指人接收到外界刺激(视觉、听觉等)的情况下大脑特定部位产生的具有一定特征的脑电信号。自发脑电则由人类自身心理活动产生。

运动想象(MI，motor imagine)是一种典型的自发脑电信号。用户想象肢体运动时，大脑皮层中会产生感觉运动节律(SMR，sensorimotor rhythms)。SMR包含mu节律和beta节律，分别位于8～13 Hz和13～30 Hz。感觉刺激、运动行为和心理意象可以改变皮层内的功能连接，并导致mu节律和beta节律出现事件相关同步(ERS，event-related synchronization)和事件相关去同步(ERD，event-related desynchronization)现象[7]。运动想象任务主要包括左手运动想象、右手运动想象、以及想象脚和舌头的运动。因此常用的运动想象解析算法为二分类或三分类算法，一般为对左右手想象的分类，对手和脚想象分类，以及对左右手和舌头想象的分类。

典型的运动想象脑电(MI EEG)信号解析算法流程包括特征提取和分类。其中，由于MI EEG信号具有非平稳性和低信噪比的性质，特征提取具有一定挑战性，同时也是研究热点。最常见的算法是共空间模式算法(CSP，common spatial pattern)及其改进方法。CSP是一种空间滤波方法，用于将EEG数据转换到一个新空间中，其中一个类的方差最大化，而另一类的方差最小化。EEG信号的不同频带包含不同的信息，而CSP 能够从特定频带中提取这些信息。研究人员尝试了许多基于CSP算法的改进方法。共空间频谱模式(CSSP，common spatio-spectral patterns)将有限脉冲响应滤波器(FIR，finite impulse response)集成到 CSP 算法中[8]。共稀疏频谱空间模式(CSSSP，common sparse spatio-spectral patterns)是对CSSP的进一步改进，旨在找到不同通道间共同的频谱模式，而非各通道独立的频谱模式[9]。子频带共空间模式(SBCSP，sub-band common spatial pattern)将脑电信号花费为若干个子频带，再对不同的子带进行滤波并对每个子带用CSP提取特征，然后使用线性判别分析方法来降低子带的维数[10]。这些改进方法相比于原始CSP算法，都能适当提高分类准确度。

循环奇异谱分析-共空间模式(CiSSA-CSP)方法可以提取非平稳信号的最优时频空间特征，相比于其他特征提取方法，该方法可以显著提高MI EEG的分类精度[14]。CiSSA将信号分解为一系列频率成分已知的重构分量，然后对每一组分量分别用CSP提取特征。CiSSA可以去除相同频率中的噪声和伪影成分，因此CiSSA-CSP方法提取到的特征具有更好的分类效果。

当前大多数脑机接口系统都是基于计算机实现的，相比较于计算机，嵌入式系统具有体积小、功耗低、成本低、响应速度快和便携式等特点，因此脑机接口系统的嵌入式实现也是脑机接口系统应用化的必经之路。Bueno等人利用16位数字信号控制器实现了运动想象三分类(左右手想象和心里想一句话)，分类准确率约为60%[11]。使用SOMANN神经网络实现分类算法，从空间滤波到分类结果输出的完整算法耗时2 ms。Ma等人出了一种基于FPGA的EEG-MI分类的纯硬件系统[12]。EEG信号被处理为连续时域中的一系列多通道图像，显示受试者 MI 期间大脑皮层的能量变化。分类准确度达到80.5%，系统耗时为计算机的，功耗为计算机的。Belwafi等人利用Stratix-IV(FPGA)实现了用于运动想象分类的嵌入式脑机接口系统[13]。使用动态滤波算法对MI EEG信号进行预处理，动态滤波算法相比静态滤波算法复杂度更低，更有利于FPGA嵌入式实现，能有效降低延时与功耗。动态滤波算法通过选择包含最活跃 ERS/ERS 模式的时间窗口，为每个用户动态选择 EEG 试验的时期。其利用CSP进行特征提取，LDA完成分类。相比于SVM、KNN等方法，LDA具有更低的算法复杂度。公共数据库数据测试，离线训练时分类准确率为77%，在线训练分类准确度达到80.25%，单次实验计算耗时0.43 s(22通道，采样时间5 s，采样频率100 Hz)。

嵌入式脑机接口系统面临的挑战包括高分类精度、稳健性和自适应性、功耗、时间响应和成本效益。在运动想象分类任务中，分类准确度应当达到80%以上，才算是可靠的脑机接口系统。系统应当具有较好的稳健性和自适应性，需要有良好的预处理算法以消除伪迹、眼电等噪声，同时不同用户的脑电信号特征具有明显差异，系统应当能适用于不同用户的信号特征。

嵌入式DSP处理器专门用于信号处理，通过对系统架构和指令算法的特殊设计，实现高效率的编译效率和数字运算。相比于FPGA、ARM等其他嵌入式平台，DSP具有更强的信号运算能力，同时可使用C语言进行编译，易于实现。

本文通过优化CiSSA-CSP算法流程，合理使用DSP库函数和关键字等优化工具，成功将CiSSA-DSP特征提取算法移植实现在DSP平台中，并利用公共数据库数据验证了其分类有效性和低延时的特性。

1 CiSSA-CSP特征提取算法原理

1.1 CiSSA原理

循环奇异谱分析(CiSSA，circulant singular spectrum analysis)是对奇异谱分析算法(SSA，singular spectrum analysis)的改进，最初由Juan Bógalo等人[15]提出，其可以有效去除与有效信号频率重叠的部分噪声和伪影。CiSSA可以将信号分解为一系列频率成分已知的重构分量，其包含四个步骤：序列嵌入、分解、分组和对角线平均。

步骤1：序列嵌入

输入为单通道脑电时序数据(x1，x2，…，…，xN)，使用窗口长度为L的滑动窗口将输入数据映射到轨迹矩阵X上。其中K=N-L+1，一般有L≪K。

(1)

步骤2：分解

与SSA中的SVD分解所不同的是，CiSSA引入了循环矩阵CL，利用循环矩阵的特征向量将轨迹矩阵分解为一系列代表不同频段的秩为1的基本矩阵。

(2)

相比于一般矩阵需要进行SVD分解以计算特征向量和特征值，循环矩阵的特征向量和特征值计算相对简单，其第k个特征值及其对应的特征向量表达式为：

(3)

(4)

(5)

循环矩阵CL的值由序列样本协方差决定。

(6)

(7)

与SSA相同，改进SSA算法中轨迹矩阵X被分解为L个子矩阵相加。

X=X1+…+XL

(8)

Xi=wiwiHX，i=1，…，L

(9)

步骤3：分组

由于循环矩阵的特征向量为复向量，因此需要通过分组配对，将复矩阵Xi转化为实矩阵。配对方法如下：

(10)

(11)

由此将原有轨迹矩阵X分解得到了一组新的子矩阵XBk。

步骤4：对角线平均

(12)

(13)

(14)

依上所述，CiSSA的算法流程如图1所示。

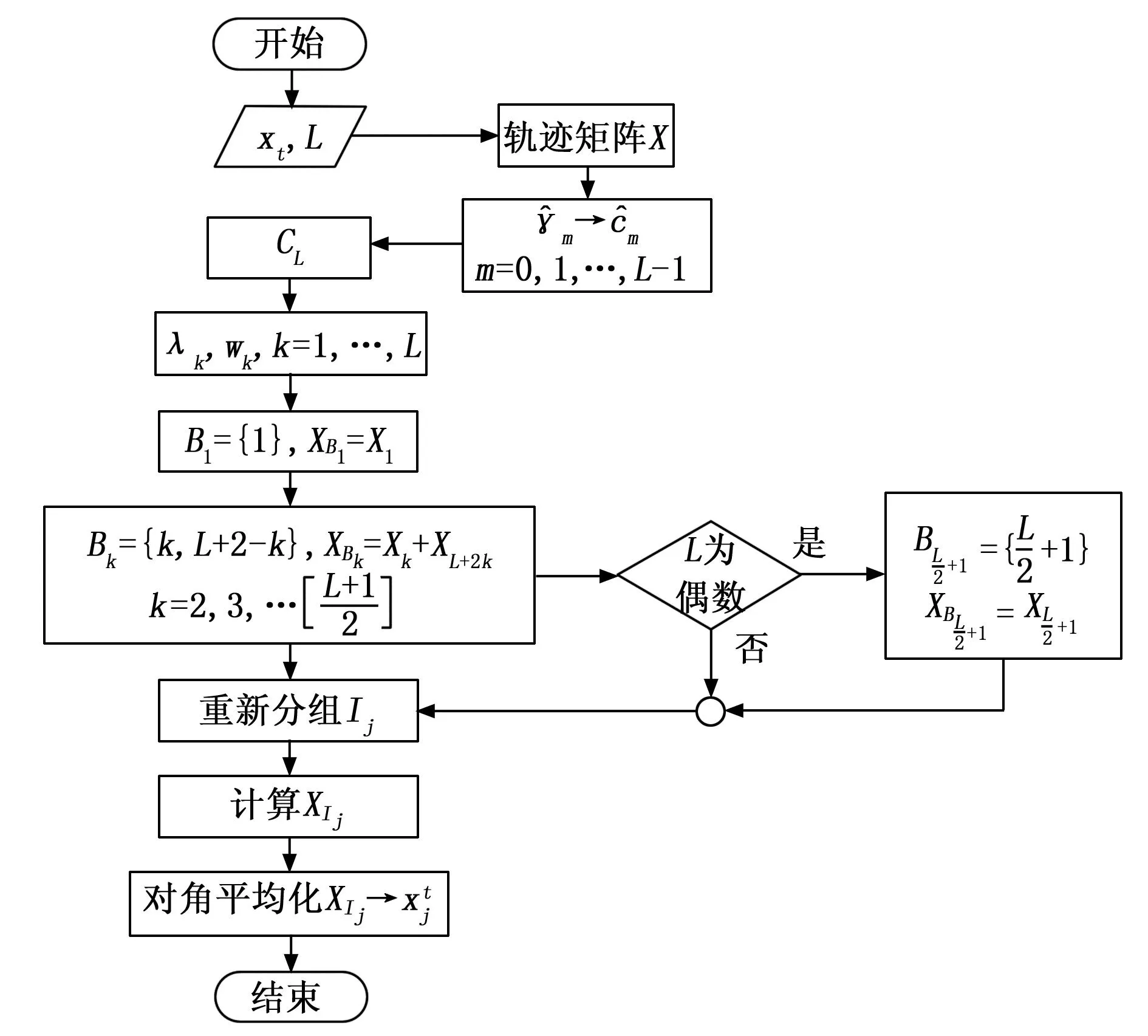
图1 CiSSA算法流程图

1.2 CSP原理

共空间模式算法(CSP，common spatial pattern)算法是一种专用于二分类的多通道信号特征提取方法，CSP通过最大化两类想象任务脑电信号方差的差异性，以提取出差异性较大的特征用于分类[16]。

首先计算各样本的协方差阵并继续归一化，然后按照所属任务类别，分别对两类任务信号的归一化协方差阵求均值，然后相加得到混合协方差阵。其中Xi为第i类样本数据，大小为NC*NS的矩阵。

(15)

(16)

通过白化矩阵P，将不同方向的特征值完成归一化。

PRPT=I

(17)

P=∑-1/2UT

(18)

R=U∑UT

(19)

UUT=I

(20)

此时两类任务的协方差阵特征值对应相加为1，因此某一类任务的方差大时，另一类任务的方差就小，接下来需要调整投影方向使得两类方差的差异尽可能大[17]。方法是将每类任务的平均协方差阵白化，并沿特征向量方向进行投影。其中特征向量的排序按照对应特征值降序排布。

(21)

Si=BΛiBT，i=1，2

(22)

BBT=I

(23)

白化矩阵沿特征向量方向投影即得到空间滤波矩阵W。空间滤波矩阵W的每一行对应一种空间投影模式，将W与样本X相乘得到空间滤波后的信号，再对该信号的每一行求方差并取对数[18]，即得到此种投影方式下的特征。

W=BTP

(24)

Z=WX

(25)

Z=[Z1，…，ZNC]T

(26)

Fi=ln(var(Zi))

(27)

其中：Λi应当按照特征值降序排布，因此Z1，…，ZNC的顺序与不同投影方向方差的差异性顺序一致，Z1代表的投影方向最大化了第一类样本投影后方差减第二类样本投影后方差，ZNC代表的投影方向则最大化了投影后第二类样本方差减第一类样本方差。因此一般选取Z的前m行和后m行来计算用于分类的特征，这2m行是将类间方差差异最大化的2m个投影方向。

(28)

依上所述，CSP算法流程图见图2。

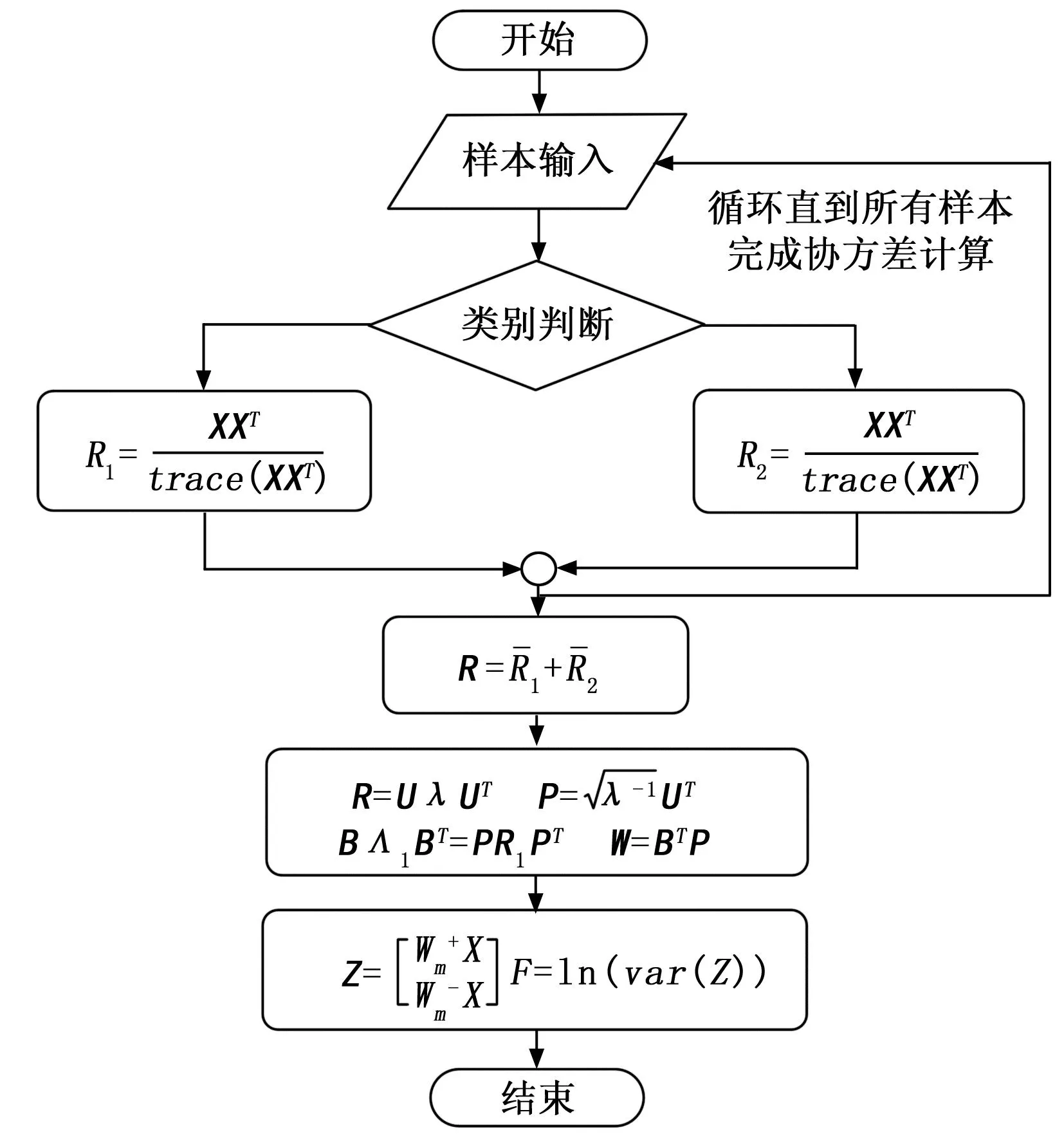
图2 CSP算法流程图

2 CiSSA-CSP特征提取算法的优化移植

2.1 移植平台和优化方法介绍

C66x系列DSP是德州仪器公司近年来推出的高端DSP芯片，具有强大的定点浮点运算能力，能用于图像处理、音频分析、信号处理等领域[20]。定点使用时，C66x核的乘加运算能力(MAC，multiply accumulate)为C64x核的4倍。同时集成了浮点运算能力和各核的原始运算能力，达到了行业领先的44.8 GMACS和22.4 GFLOPS(在1.4 GHz工作频率下)。单个周期内可以执行8次单精度浮点MAC操作，也可以执行双精度和混合精度操作。本文采用的是C66x系列的TMS320C6678DSP，C6678集成了8个C66x内核，其主频率最高可到1.4 GHz[19]。为方便实现，没有自己设计接口电路，直接选用现有的开发板以初步实现功能。本文选用的是广州创龙公司的TL6678-EasyEVM开发板。开发板上已预先烧入了初始化程序，并引出GPIO、SPI等外设接口，使用开发板可以大大方便我们的调试工作。

软件开发平台采用软件编译平台CCS(code composer studio)，版本为v5.5。CCS中集成了多个开发套件，同时支持C语言、C++等语言，且提供了方便的调试环境，利于用户调试代码程序。同时还需要仿真器用于连接电脑和DSP开发板。仿真器通过USB接口与电脑相连，通过JTAG接口与开发板相连。通过仿真器才可以将CCS中程序写入DSP并利用CCS控制调试DSP。选用的仿真器是创龙公司的TL-XDS200仿真器。

DSP软件优化主要包含两个方面，算法和编译。算法优化指重新设计算法流程，通过数学手段降低计算复杂度。编译优化指优化代码实现方式，通过合理编译，减少计算耗时。CCS中有编译器优化选项，分别为off，0，1，2，3五档，off代表无优化，0代表寄存器级别优化，1代表局部优化，2代表全局优化，3代表工程文件整体优化[21]。我们选用～2级别优化，其可以实现高效率的编译同时也方便进行程序调试。C语言优化也可以提高编译效率，其主要从两个角度着手，其一是使用各类关键字或编译指令告知编译器更多信息，让编译器能更好的对C语言进行编译；其二是使用专用于相应型号DSP的C语言函数，这些函数由德州仪器公司编写提供，已专门针对相应DSP做了特定优化[22]。

2.2 CiSSA算法优化

MI EEG信号的特征频段集中在mu节律和beta节律，同时我们并不需要各分量的功率谱信息，因此，我们无需计算循环矩阵的特征值。由式(3)～(5)可知，循环矩阵的特征向量只与L有关，而与循环矩阵中元素数值无关，因此在DSP上实现改进SSA实现时，无需计算cm，求出特征向量后，利用式(9)，即可求出子矩阵。但由于特征向量为复向量，因此子矩阵Xi为复矩阵，这在DSP硬件上实现并不划算。因此实际移植到DSP上时，希望跳过复矩阵的计算步骤，直接得到配对后的实矩阵。利用式(5)、(11)和(12)，计算得到XBk。XBk的公式如下：

(29)

(30)

(31)

(32)

由式(29)、(31)计算得到XBk后，对角平均化即可得到原时间序列的相应分量。由上述公式推得的改进SSA算法流程见图3。相比于图1，此处算法流程省去了计算循环矩阵和复特征向量的步骤，得到了显著简化，更适于移植到DSP上。

图3 CiSSA优化后算法流程图

2.3 CiSSA算法移植与复杂度分析

是MI EEG信号特征集中在mu节律(8～13 Hz)和beta节律(13～30 Hz)上，因此在利用改进SSA算法处理运动想象脑电信号时，只需要提取出8～30 Hz范围内信号分量，其他频段的信号都不需要。在DSP实现时，应当首先筛选出需要的分量，然后只用计算相应的分量即可，不用计算所有的分量，以降低运算量。设所需分量k的取值集合记为Range，由式(13)推得Range计算公式如下：

(33)

由式(31)注意到VBk的取值只与k和L有关，与待处理信号的值无关。因此在DSP上改进SSA算法时，首先根据上式计算出Range，再计算需要用到的VBk并保存。这样在处理不同信号样本时，VBk可以直接调用已有的数据，不用重复计算，以节省计算时间。

在实际应用中，有两个阶段：通过大量样本训练模型阶段和单次实验信号解析阶段。训练模型阶段指利用大量已有信号样本训练得到算法中的各类模型参数。

图4描述的是移植到DSP上的用于脑电信号预处理的改进SSA算法流程，用于对单个样本信号进行预处理。不过不论是单次实验信号解析还是大量样本训练分类模型，预处理都是必不可少的一步。因此在单次实验信号解析与训练分类模型过程中，预处理都按照图4的流程进行。

图4 CiSSA移植后算法流程图

假设运动想象脑电信号中包含Nc个通道数据，采样频率为fsHz，单次实验采样时间为T秒，则单次实验信号为Nc×Ns的数据矩阵。假设Range的元素个数为numK。

Ns=fs×T

(34)

Range的算法复杂度可忽略不计，计算numK个Vbk的复杂度为O(numK×L2)；嵌入轨迹矩阵的复杂度为O(L(Ns-L+1))=O(LNs)；计算numK个XBk的复杂度为O(numK×L2(Ns-L+1))=O(numK×L2Ns)，对角平均化的复杂度为O(numK×LNs)。

通过上述分析可知，移植到DSP上的改进SSA算法中，计算量最大的部分就是XBk的计算，这一步是单纯的矩阵乘法，共需要L2(Ns-L+1)次浮点乘加运算，而在单次实验信号处理中，对单通道下Range中每一个k要计算一次，因此其一共需要L2(Ns-L+1)Nc×numK次浮点乘加运算。

2.4 CSP算法移植与复杂度分析

为提高运行效率，在移植过程中应当多使用DSP的库函数，这些函数都专门针对DSP结构进行了优化，执行效率很高。CSP算法中有两步特征分解，而德州仪器公司所编写的dsplib库(3.4.0.0版本)中提供了单精度数值矩阵SVD分解函数，函数名为DSPF_sp_svd。而对于方阵而言，SVD分解就是特征分解，因此移植时使用该函数来完成特征分解的步骤。

如2.3节所述，实际应用中分为模型训练和单次实验信号解析两个阶段，模型训练阶段算法与2.2节所述一致。移植后算法流程见图5。而在单次实验信号阶段，已有空间滤波矩阵W，此时只需将W的前m行和后m行与样本相乘，并对结果的每一行方差取对数即可完成特征提取，移植后算法流程见图6。

图5 CSP移植后模型训练阶段流程图

图6 CSP移植后单次实验信号解析阶段流程图

模型训练阶段中，对nT个样本计算归一化协方差矩阵的复杂度为O(nT×Nc2Ns)，特征分解和矩阵乘法的复杂度为O(Nc3)，其余步骤算法复杂度可忽略不计。在MI EEG信号中，一般有Nc≪Ns，因此由上述分析可知，CSP整体算法复杂度为O(nT×Nc2Ns)。而在归一化协方差矩阵计算中，矩阵乘法XXT需要Nc2Ns次浮点乘加运算，trace(XXT)需要Nc次浮点加法运算，归一化需要Nc2次浮点除法运算。由于浮点除法运算相比于乘法更消耗时间，因此移植到DSP时，为节省时间，可以将除法运算转化为乘法运算，即先求出trace(XXT)的倒数，之后每次与该倒数相乘即可。这样只用计算1次除法和Nc2次乘法。单次实验信号解析阶段的算法复杂度为O(2m×Nc×Ns)，相比于2.3节所述CiSSA复杂度可忽略。

2.5 CiSSA-CSP整体算法移植与内存分配

模型训练阶段的CiSSA-CSP移植后整体算法流程如图7所示。注意到样本数据是存储在MSMCRAM中的，经过预处理后，再存储到DDR3上，这是因为CSP需要nT个样本的数据，而MSMCRAM可能无法提供足够的存储空间。以公开数据库数据为例，nT=280，Nc=17，Ns=350，假设Range={3，4，5，6，7，8}，即numK=6，于是280个样本经过CiSSA预处理后，有numK×nT×Nc×Ns=9 996 000个数需要存储。假设在DSP中把数据存为单精度格式，一个单精度数需要4B存储空间，则结果预处理得到的所有数据至少需要39 047 MB的存储空间，而在C6678上MSMCRAM只有4 096 MB的空间，而DDR3有1 GB空间，可以满足要求。因此需要将经过CiSSA预处理的数据存储到DDR3上。

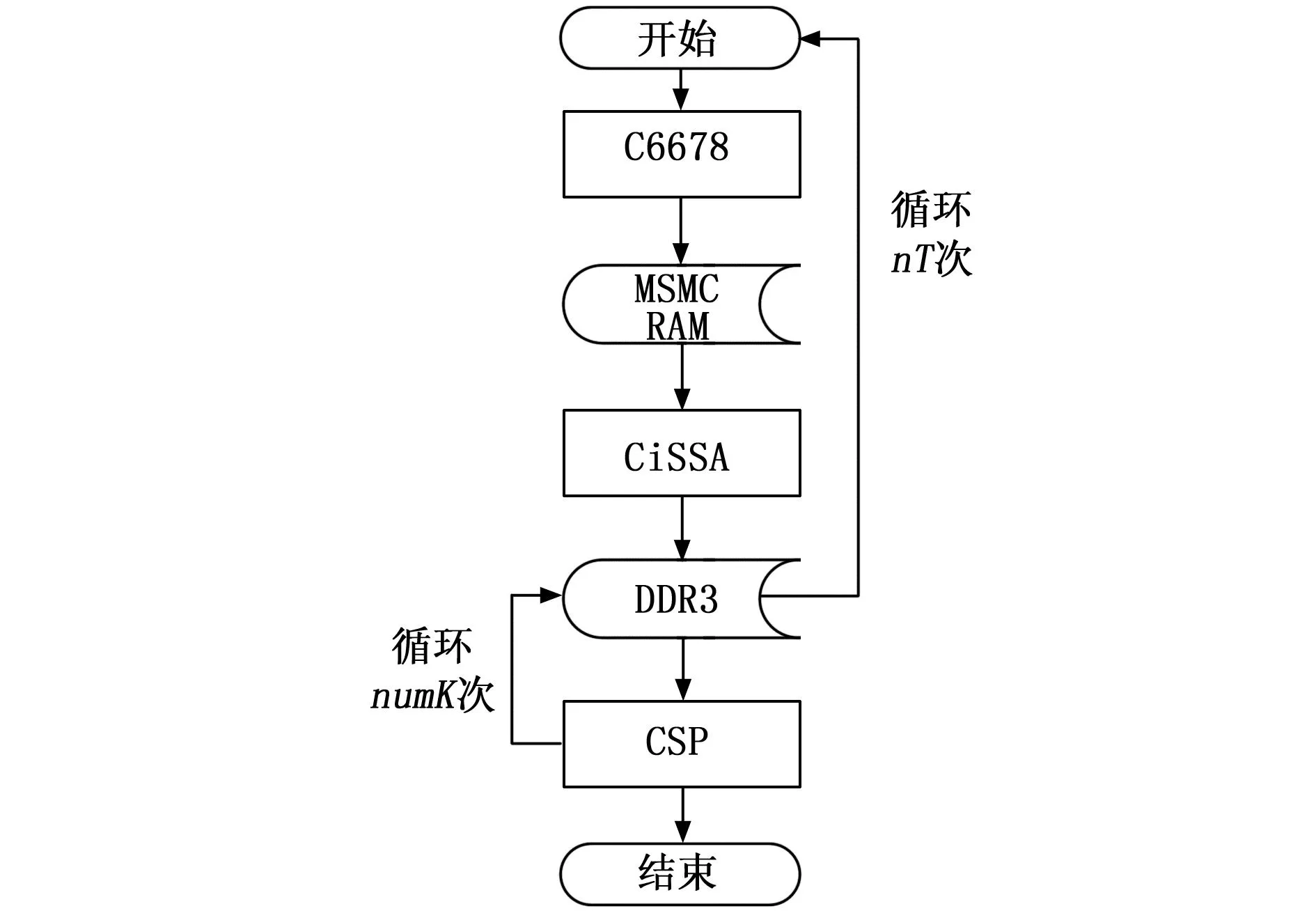
图7 模型训练阶段CiSSA-CSP移植后算法流程图

单次实验信号解析阶段中已有分类参数，CSP模块算法得到极大简化，而CiSSA模块的算法不变。此时整体算法流程图见图8。CiSSA模块中无需计算Range，Vbk，其已经计算好并存储在内存中了，同样的CSP模块中各分量的空间滤波矩阵Wk也已储存在内存中，需要时直接调用即可。单次实验数据处理中则无需使用DDR3存储空间，所有内存均存放在MSMCRAM上。

图8 单次实验信号解析阶段CiSSA-CSP移植后算法流程图

3 移植测试实验结果

C语言算法通过CCS平台编译并移植到C6678DSP开发板上，本节将对移植到DSP上的算法进行测试，一方面与在电脑上使用Matlab计算的结果对比以验证计算准确性，另一方面测试使用DSP完成计算所消耗的时间。其中PC端处理器为Intel i5-8250 CPU，机带RAM为8 GB，Matlab版本为2021b；C6678开发板上仅使用核0进行运算，另外7核未启动，芯片主频设定为1.0 GHz，信号存储及运算均在32位浮点数精度下实现。

3.1 数据来源

用于测试的数据来源于BCI Competition Ⅲ，选用的数据集是data set ⅠVa，其中包含5个健康受试者的数据[23]。受试者进行右手和右脚的运动想象实验，使用国际通用的10～20系统电极排布方式，共有118个通道[15]。每个受试者进行280次实验，每个想象任务140次，单次实验为持续3.5秒的运动想象，两次想象间隔为1.75～2.25秒，采样频率为100 Hz。处理数据时选择所有通道中与运动想象相关的17个通道(FC3，FC1，FCz，FC2，FC4，C5，C3，C1，Cz，C2，C4，C6，CP3，CP1，CPz，CP2，CP4，如图9所示)[24]，因此单次实验样本数据为17*350的矩阵。

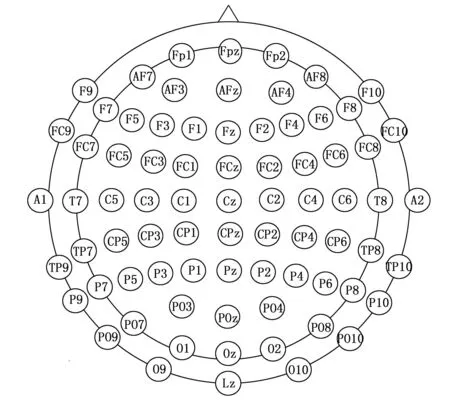
图9 公共数据库信号通道分布图

3.2 CiSSA-CSP特征提取算法移植误差测试结果

取L=24，可得Range=(3，4，5，6，7，8)，numK=6。于是单个信号样本经过CiSSA算法预处理后，得到6个与原信号大小一致的矩阵。取m=2，即一个信号样本矩阵通过CSP特征提取后，得到2m=4个特征值。于是原信号一共提取出24个特征。对比DSP上运行CiSSA-CSP算法得到的特征与PC机上MATLAB计算的特征，结果见表1，平均相对误差在10-4量级。其中绝对误差为DSP运算得到特征减去PC机上MATLAB计算得到特征的绝对值，相对误差为DSP运算得到特征减去PC机上MATLAB计算得到特征的绝对值再除以PC机上MATLAB计算得到特征。

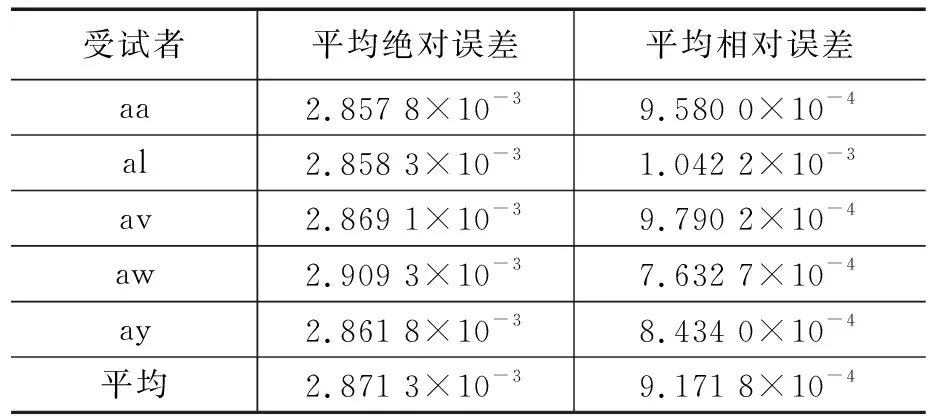
表1 CiSSA-CSP误差测试

注意到CiSSA-CSP算法步骤中，就计算类型而言主要分为两种：矩阵乘法和特征分解。矩阵乘法采用DSP库函数实现，误差相对较小，我们用生成的随机方阵检验了特征分解的误差，结果见表2，其中方阵大小为N×N。单次特征分解的相对误差在10-5量级，而CiSSA-CSP运算中有两步特征分解，两步误差累积可达10-4量级，这与表1的结果相吻合，说明移植后CiSSA-CSP特征提取算法的主要误差来源为特征分解。

表2 特征分解误差测试

3.3 CiSSA-CSP特征提取算法移植耗时测试结果

表3测试了CiSSA运算耗时与式(29)单步运算耗时。在单次实验信号解析中，CiSSA运算中需要计算17×6=102次式(29)，由表3结果可得式(29)的计算耗时占比达到预处理模块计算耗时的94.49%。这与我们在2.3节中复杂度分析的结果相吻合。

表3 CiSSA耗时测试 ms

矩阵乘法函数是CiSSA-CSP运算过程中的核心步骤，我们使用关键字、编译器优化等方式，对乘法函数文件进行了优化。表3中也给出了优化后CiSSA的耗时测试结果，优化后耗时仅为优化前耗时的14%。

训练模型阶段，CSP运算的耗时测试结果见表4，其中单次协方差计算为式(15)。此时特征提取模块算法中，共包含280次协方差计算(共280个样本)，所有样本的协方差计算耗时在特征提取模块中耗时占比达94.03%。在训练模型阶段，特征提取模块对时间消耗并不敏感，对耗时敏感的是单次实验信号解析。而在单次实验信号解析阶段中，其耗时测试结果见表5。与CiSSA耗时相比，单次实验信号解析中CSP的耗时可以忽略，这与2.4节分析的结果一致。

表4 CSP耗时测试(模型训练阶段) ms

表5 CSP耗时测试(单次实验信号解析阶段) ms

3.4 移植后分类测试结果

CiSSA-CSP特征提取算法移植到DSP后的有效性需要依赖MI EEG信号分类精度来确认，因此我们将在DSP上还移植实现了LDA分类算法，并对完整算法流程进行了测试，比较相同样本在DSP上运算的分类精度和MATLAB上运算的分类精度。分类精度测试采用10折交叉验证，结果见表6。DSP运算的分类精度相比于PC机上Matlab计算结果下降小于0.5%，且平均分类精度达到93.2%。同时LDA的耗时相比CiSSA-CSP可以忽略不计，而由3.3节结果可知，单次实验信号解析阶段中CiSSA-CSP在DSP运算的耗时小于150 ms，满足MI EEG分类实时性的要求。

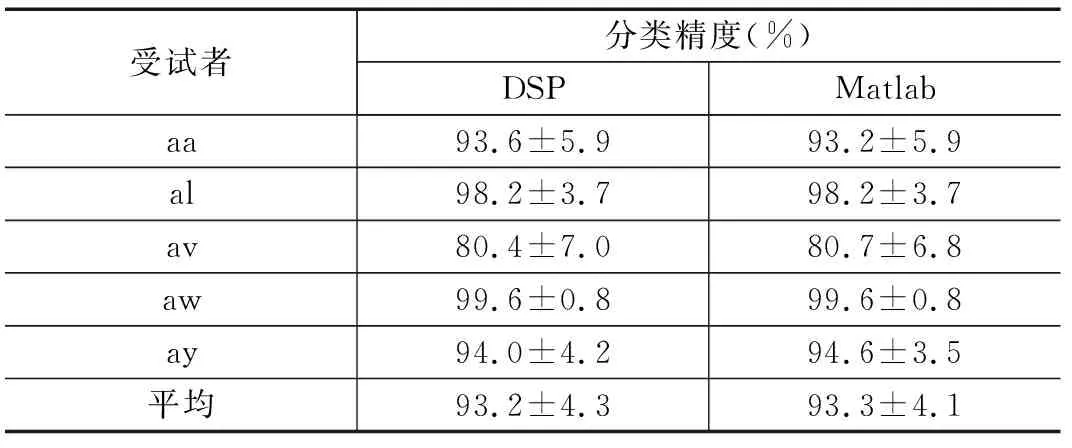
表6 DSP运算与PC机上Matlab运算分类精度对比

4 结束语

本文通过优化CiSSA算法、合理规划整体算法流程、使用CCS编译器优化工具等方法成功在C6678DSP开发板中移植实现了CiSSA-CSP特征提取算法，并使用MI EEG公共数据库数据验证了算法的准确性，分类准确度相比于PC机上Matlab运算结果下降小于0.5%。同时单次实验信号解析耗时少于0.15 s，满足了解析实时性的要求。