基于卷积注意力特征迁移学习的滚动轴承故障诊断

邹 建

(成都天奥测控技术有限公司，成都 611731)

0 引言

滚动轴承作为机械装备中被广泛使用的零部件之一，对其进行故障诊断可以大幅度提高机械装备的工作稳定性[1]。滚动轴承通常在变工况条件(如转速不同、受力大小以及受力方式不同等)下工作，复杂的变工况条件不仅会造成轴承各类故障(例如：轴承内圈故障，轴承外圈故障，滚动体故障)，同时由于轴承当前工况的类标签很难获取甚至无法获取，造成滚动轴承故障诊断当前工况(即源域)可用样本少。此外，不同的工况也会导致历史工况(即目标域)样本与当前工况样本之间的概率分布存在差异，包括边缘概率分布和条件概率分布。因此，利用历史工况下的有标签样本对当前工况的滚动轴承样本进行故障诊断具有重要意义，但也面临着挑战。

目前滚动轴承故障诊断方法主要分为信号处理法、解析模型法和数据驱动法三类[3]。3种方法的共同点在于都需要提取特征值作为故障识别的基础，而且都依赖于阈值判断；不同之处在于辨识模型的差异：信号处理法能够快速实现在线诊断而且利用小波分析可以最大程度的保证故障诊断准确性，但是需要对研究对象熟悉度高，并且选取故障特征值较困难而且通用性差。解析模型不需要先验知识而且有较快的诊断速度，但是对模型的准确性要求较高，容易因参数偏差、采样误差等外界因素带来模型估计误差，从而影响诊断结果的准确性。数据驱动法结合人工智能算法实现故障特征的自动分类与识别，不需要了解系统模型与工作机理，抗扰性强，对于复杂系统的故障诊断具有明显优势，但是该类方法相对复杂、依赖大量历史数据并且其诊断速度依赖于算法自身的计算复杂度以及计算机的硬件性能。

由于计算机性能的提升使得诊断速度慢的问题可以得到有效解决，因此选择利用历史工况数据驱动法来解决变工况条件下的滚动轴承故障诊断问题已成为研究热点和技术趋势。文献[4]将通道注意力机制引入多尺度非对称卷积模块用于提取滚动轴承故障特征，然后将多尺度非对称卷积模块中的全连接层改进为胶囊全连接层用于对滚动轴承进行故障分类。文献[5]引入均匀化分布Chebyshev混沌映射和自适应惯性权重到麻雀算法中，提高麻雀算法(SSA，sparrow search algorithm)的全局和局部搜索能力，并将该改进的麻雀算法用于支持向量机(SVM，support vector machine)的参数优化，优化后的支持向量机再用于对滚动轴承的故障信号进行分类诊断。文献[6]将全局可微的稀疏模型引入深度神经网络来学习具有数据协同链接性能的深度网络稀疏去噪(DNSD，deep network-based sparse denoising)网络的超参数，并利用优化后的该网络对模拟滚动轴承故障信号数据集进行故障诊断。文献[7]利用卷积神经网络(CNN，convolutional neural network，)从时频图像中提取滚动轴承固有故障的特征。最后，将提取的特征输入到gcForest分类器中，以实现对滚动轴承故障的准确诊断。文献[8]利用变分频域特征提取器提取特征，然后局部异常因子对离群点进行剔除，最后将特征输入分类器对滚动轴承进行故障诊断。

然而，以上基于传统机器学习的数据驱动方法都是基于概率分布一致的假设，并且在提取特征时缺乏对样本特征本身的深度提取和信息融合，因此在变工况条件下的域泛化能力[9]以及诊断精度并不高。迁移学习[10](Transfer Learning)具有良好的域泛化性能，能适应变工况条件下样本概率分布不一致的问题；而多头自注意力机制[11](Multi-Head Self-Attention Mechanism)能有效考虑到样本特征提取时的信息融合问题，即它能将深层分类信息融合进卷积特征提取网络[12]中，使所提取的特征有更好的分类性[13-14]。因此，本文结合迁移学习、多头自注意力机制和卷积神经网络的各自优势，提出了一种具有更好的域泛化性能和分类性能的新型迁移学习方法——卷积注意力特征迁移学习(CAFTL，convolutional attention-based feature transfer learning)用于滚动轴承故障诊断，该方法可提高变工况条件下的滚动轴承故障诊断准确性。

1 CAFTL理论模型

CAFTL主要由卷积多头自注意力特征提取网络和域自适应迁移学习网络构成。首先，对空间滚动轴承原始振动加速度信号样本做适应多头自注意力输入形式的编码预处理，得到对应的注意力分数之后，将注意力分数与源域以及目标域样本相加，再经过归一化层，归一化层输出的结果再输入到卷积神经网络中得到对应的源域和目标域特征；然后通过域自适应迁移学习网络将两域特征投影到同一个公共特征空间内，接着利用由源域有标签样本构建的分类器进行分类。最后，利用随机梯度下降法对整个CAFTL进行训练和更新，得到CAFTL对目标诊断任务的最优参数，再利用训练好的CAFTL对待测样本进行故障诊断。

1.1 卷积多头自注意力特征提取网络

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

然后，利用缩放点积方式计算源域和目标域样本多头自注意力：

(9)

(10)

图1 多头注意力计算示意图

(11)

(12)

(13)

(14)

1.2 域自适应迁移学习网络

提取到高维特征后，通过分布差异度量函数φ(·)来构造如下高维特征迁移损失函数l(θ)：

(15)

于是可以通过优化该特征迁移损失函数来学习域自适应迁移学习网络的参数集θ，以实现源域样本高维特征向目标域样本高维特征的迁移，使得它们之间的概率分布差异最小化。

接下来，利用由源域有标签的样本构建的分类器对同分布的目标域待测样本进行分类。首先计算目标域待测样本的高维特征与源域带类别标签样本特征的相似度，相似度度量函数为ζ(·，·)，并选择相似度最大的源域高维特征所对应的类标签作为滚动轴承目标域待测样本的预测伪类标签kl(kl代表目标域第l个样本对应的伪类标签)，该过程表达如下：

(16)

随后，计算该目标域待测样本属于伪类标签kl的概率如下：

(17)

接下来，将所有目标域待测样本属于其对应的伪类标签概率的负对数之和作为分类损失函数Φ(θ)，该分类损失函数推导如下：

(18)

然后，结合域自适应迁移学习网络的特征迁移损失函数l(θ)以及分类损失函数Φ(θ)作为CAHTL的联合损失函数数Γ(θ)，该联合损失函数表达如下：

Γ(θ)=ρl(θ)+Φ(θ)=

(19)

式(19)中，ρ为联合损失函数的平衡约束参数，分别用于约束域自适应迁移学习网络的局部寻优行为。

使用随机梯度下降法(SGD)将CAFTL的联合损失函数训练至收敛。假设第λ次训练CAFTL学习网络的参数初始值集合为θλ，则参数更新过程表达如下：

θλ+1=θλ-α▽θΓ(θλ)=θλ-α▽θ[ρl(θ)+Φ(θ)]=

(20)

待CAFTL训练完成后，就完成对CFHTL网络的参数微调，此时得到CAFTL对该任务的最优参数θ*，也即完成对CAFTL的训练。

(21)

2 基于CAFTL的滚动轴承故障诊断方法

基于CAFTL的滚动轴承故障诊断方法的实现过程如图2所示，具体说明如下：

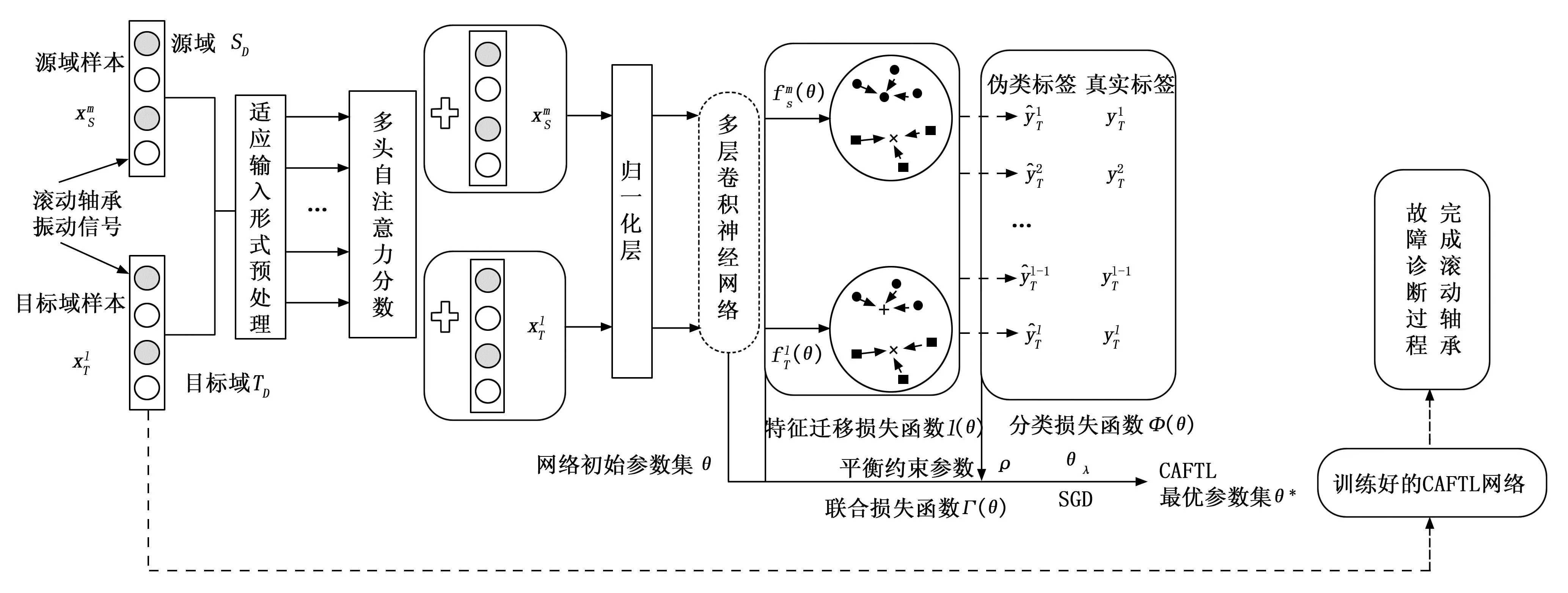
图2 基于CAFTL的滚动轴承故障诊断方法实现过程

1)将滚动轴承源域(即历史工况)带标签样本和目标域(即当前工况)待测样本进行域切分并矩阵变换后，计算各自的多头自注意力分数，然后将多头自注意力分数与源域、目标域样本相加，再经过层归一化处理，层归一化处理后得到的计算结果输入到卷积神经网络中得到对应的源域和目标域样本的高维特征。

2)将源域样本的高维特征和目标域样本的高维特征通过域自适应迁移学习网络迁移到同一公共特征空间内，并且构造域自适应迁移学习网络的特征迁移损失函数。通过优化该特征迁移损失函数以达到将不同分布的样本在公共特征空间内最大化同分布的目的。

3)利用由源域有标签的样本构建的分类器对同分布的目标域待测样本进行分类，并且构造分类损失函数。

4)结合特征迁移损失函数和分类损失函数来构造CAFTL的联合损失函数，采用随机梯度下降法将联合损失函数训练至收敛，完成对CAFTL参数的微调，即得到CAHFL的最优参数集。

5)将训练好的CAFTL用于对目标域待测样本的分类，完成滚动轴承的故障诊断全过程。

3 实验分析

3.1 实验装置

本文使用的实验数据来自凯斯西储大学电气工程实验室滚动轴承数据中心。实验使用了驱动端滚动轴承(型号为SKF6205—2RS)的振动加速度数据作为实验数据源(实验平台如图3所示)。为了模拟故障情况，实验室通过采用电火花加工的方式，在轴承的内圈、外圈和滚动体上各加工了一个小槽，槽的直径为0.335 6 mm，深度为0.279 mm。信号采集仪以12 kHz的采样频率采集了C1、C2和C3三种工况下的滚动轴承振动加速度信号。每个样本由连续的1 024个振动加速度数据点组成。在每种工况下，分别获得了约220个内圈点蚀故障、外圈点蚀故障、滚动体点蚀故障和正常状态的样本，总共有220×4个样本。

图3 凯斯西储大学滚动轴承故障模拟实验平台

表1中被标记为工况C4的实验数据是来自Cincinnati大学的常规滚动轴承加速寿命试验数据。如图4所示，将4个型号为ZA-2115双列滚子轴承安装在轴承试验台的旋转轴上，使用转速为2 000 r/min的电机通过皮带驱动转轴，并通过弹簧机构在转轴和轴承上施加6 000 lbs的径向载荷，采样频率为20 kHz，每10 min采集一次轴承的振动加速度数据。对每次采集的加速度数据截取前1 024个连续点作为一个样本，共获得1号双列滚子轴承全寿命期的984个样本。

表1 实验工况表

图4 Cincinnati大学滚动轴承加速寿命退化实验台

为了更真实地模拟工业现场环境，对表1中所有工况下的全部故障的振动加速度数据加入高斯白噪声，使这些数据的信噪比为-2 dB。

3.2 基于CAFTL的故障诊断方法的参数设置

CAFTL参数设置如下：特征提取网络中小区域样本切分个数H=32，小区域长度d=32；多头自注意力头数为4头(g=4)，每个头的输入向量维度为8维；特征映射函数F(·)都采用五层的卷积神经网络，该网络的具体配置如表2所示；域自适应迁移学习网络中的分布差异度量函数φ(·)选择最大均值差异(MMD，Max Mean Discrepancy)[15]，即：

表2 五层卷积神经网络结构表

(22)

(23)

式中，a、b分别表示向量；故障类别数K=4；平衡约束参数ρ=0.7；CAFTL网络参数学习率α=2e-4。基于CAFTL的故障诊断方法的参数设置好后在以下的所有实验中就一直保持不变。

3.3 对比实验一

在本实验中，将工况C1下的滚动轴承内圈故障、外圈故障、滚动体故障以及正常状态样本作为源域(有标签样本)，工况C3下样本作为目标域(无标签样本)用于滚动轴承故障诊断实验(即：C1→C3)。实验开始之前，在源域中按照1∶3∶4∶1的比例选取内圈故障样本数为40，外圈故障样本数为120，滚动体故障样本数为160和正常状态样本数为40用作源域有类标签训练样本；在目标域按照2∶1∶3∶3的比例选取内圈故障样本数为60，外圈故障样本数为30，滚动体故障样本数为90和正常状态样本数为90用作目标域待测样本。按照第2节所述的基于CAFTL的故障诊断方法的实现流程，将源域和目标域样本输入到设置好参数的CAFTL来对工况C3下的滚动轴承进行故障诊断。实验结束后，将本文所提出的CAFTL获得的各故障诊断准确率和平均诊断准确率与其他4种典型迁移学习方法，即：中心力矩匹配[17](CMD，central moment matching)、域迁移多核学习[18](DTMKL，domain transfer multiple kernel learning)、迁移联合匹配[19](TJM，transfer joint matching)和分发匹配嵌入(DME，distribution matching embedding)做了比较。其中，使用了k折交叉验证方法来优化CMD、DTMKL和TJM的参数以确保它们能够获得最高的滚动轴承故障诊断精度。优化后的参数如下：对于CMD，其学习速率为η=e-2，其平衡约束参数为λ=0.30；对于DTMKL，其正则化参数为λ=0.30，其子空间维数为D=3；对于TJM，其正则化参数为λ=0.25，其子空间维数为D=4；对于DME，其惩罚因子为λ=0.25。为了降低随机性带来的误差，每种方法取了前20次实验结果的平均值作为最后的实验结果，实验对比结果如表3所示。同时为了直观地验证CAFTL迁移和分类的有效性，利用t-分布随机邻域嵌入 (t-SNE，t-distributed stochastic neighbor embedding)算法[20]将CAFTL以及其它4种被对比方法提取到的高维特征降维到二维平面，并以散点图的形式呈现在图5～9中。

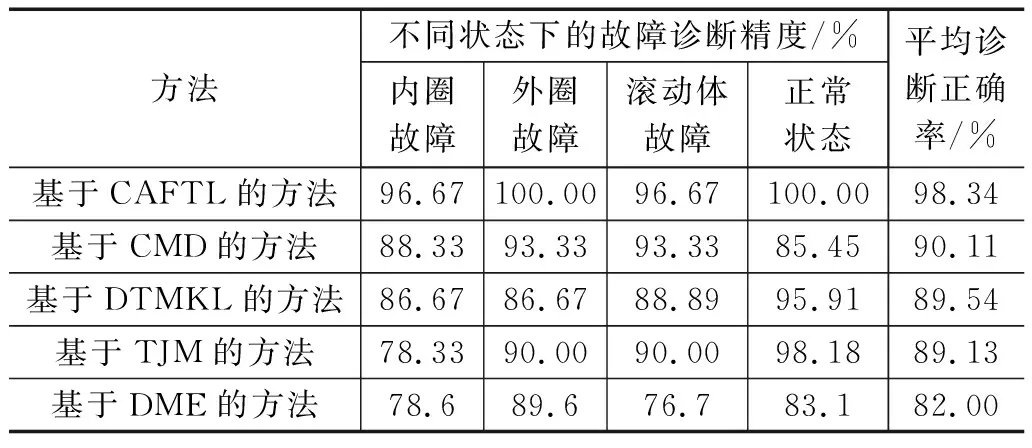
表3 C1→C3时4种迁移学习方法的故障诊断准确率

图5 CAFTL输出的高维特征经t-SNE降维后的散点图

图6 CMD输出的高维特征经t-SNE降维后的散点图

图7 DTMKL输出的高维特征经t-SNE降维后的散点图

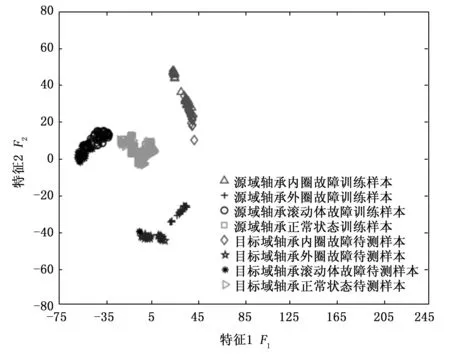
图8 TJM输出的高维特征经t-SNE降维后的散点图

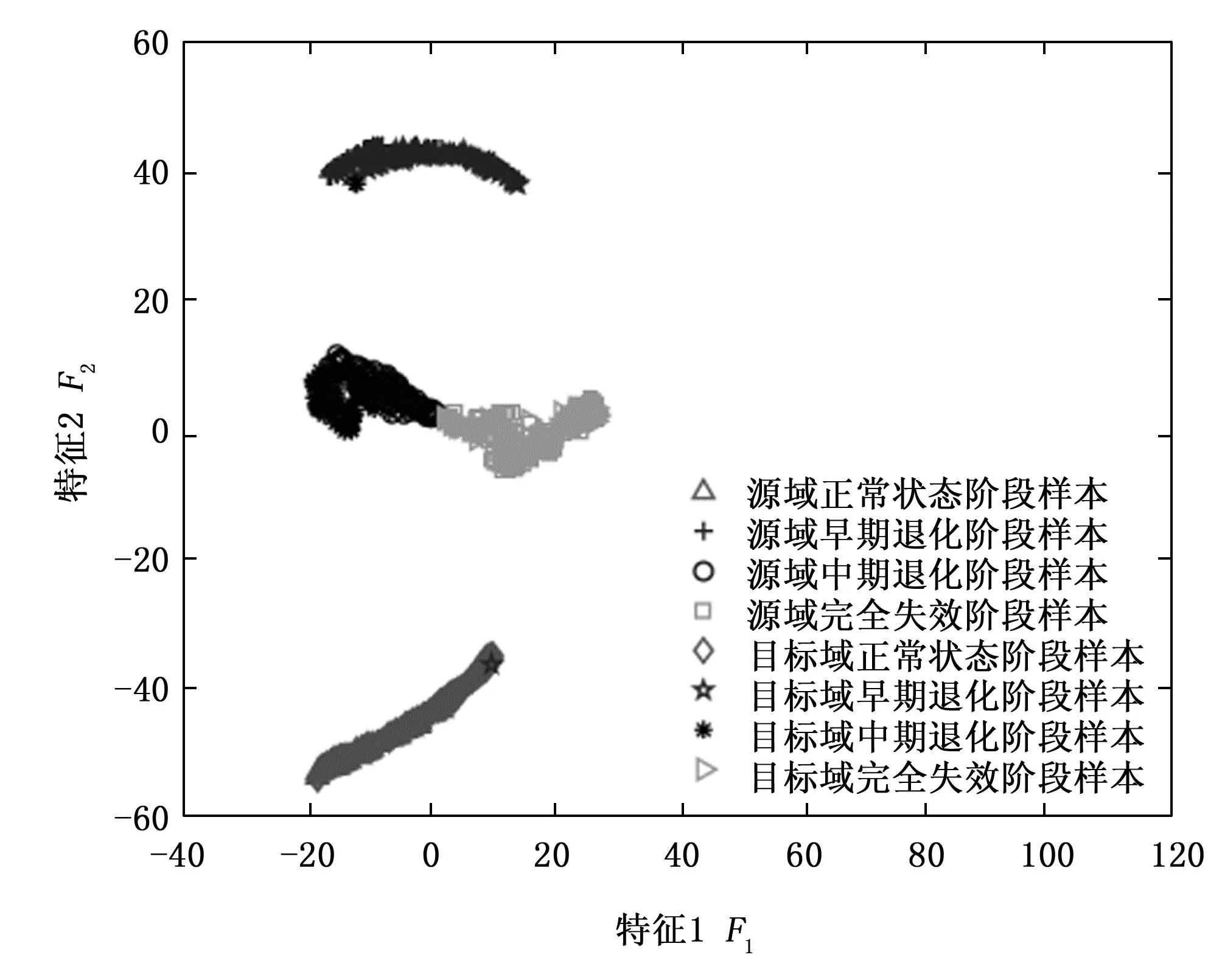
图9 DME输出的高维特征经t-SNE降维后的散点图

由表3可知，基于CAFTTL的方法在源域和目标域样本所处的工况条件不同并且对两域样本都增加了高斯白噪声的情况下，依旧保持着良好的分类性能，并且分类精度始终优于基于CMD的故障诊断方法、基于DTMKL的故障诊断方法、基于TJM的故障诊断方法以及、基于DME的故障诊断方法。由图5～9的对比结果亦可知，所提出的CAFTL相比CMD、DTMKL、TJM和DME这4种迁移学习方法能使得源域和目标域中相同类别的样本更好地聚合在一起，且能使两域中不同类别的样本之间也相对更为分散，因此相比后4种迁移学习方法，CAFTL的迁移和分类性能更好，从而基于CAFTL的滚动轴承故障诊断方法的诊断精度也就更高。

3.4 对比实验二

在本实验中，将工况C1下的滚动轴承内圈故障、外圈故障、滚动体故障以及正常状态样本作为源域(有标签样本)，工况C3下样本作为目标域(无标签样本)用于滚动轴承故障诊断实验(即：C1→C4)。实验开始之前，在源域中按照4∶1∶2∶3的比例选取内圈故障样本数为160，外圈故障样本数为40，滚动体故障样本数为80和正常状态样本数为120用作源域有类标签训练样本；在目标域按照2∶1∶4∶3的比例选取内圈故障样本数为80，外圈故障样本数为40，滚动体故障样本数为160和正常状态样本数为120用作目标域待测样本。按照第2节所述的基于CAFTL的故障诊断方法的实现流程，将源域和目标域样本输入到设置好参数的CAFTL来对工况C4下的滚动轴承进行故障诊断。为了降低随机性带来的误差，每种方法取了前20次实验结果的平均值作为最后的实验结果，实验对比结果如表4所示。

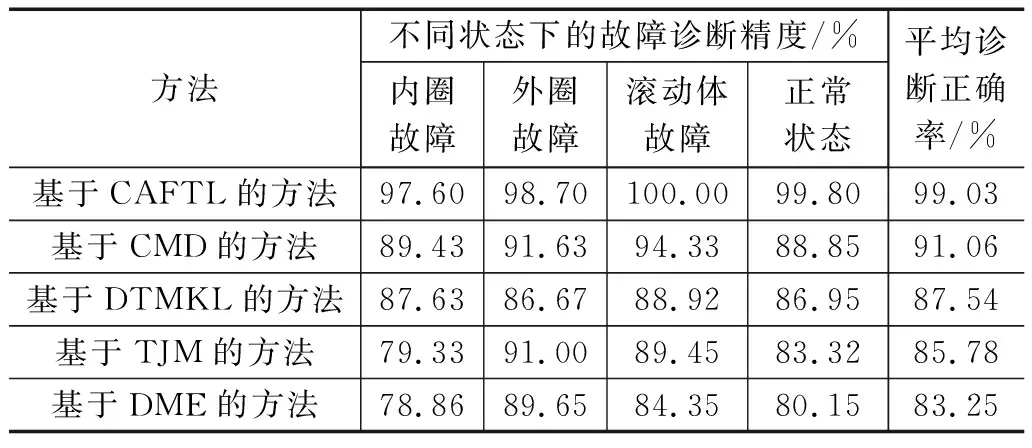
表4 C1→C4时4种迁移学习方法的故障诊断准确率

由表4可知，在源域和目标域样本概率分布不一致的前提下，基于CAFTL的方法在源域和目标域样本所处的工况条件不同并且对两域样本都增加了高斯白噪声的情况下，依旧保持着良好的分类性能，并且分类精度始终优于基于CMD的故障诊断方法、基于DTMKL的故障诊断方法、基于TJM的故障诊断方法以及、基于DME的故障诊断方法。

3.5 消融实验

实验开始之前，在源域中按照4∶1∶2∶3的比例选取内圈故障样本数为160，外圈故障样本数为40，滚动体故障样本数为80和正常状态样本数为120用作源域有类标签训练样本；在目标域按照2∶1∶4∶3的比例选取内圈故障样本数为80，外圈故障样本数为40，滚动体故障样本数为160和正常状态样本数为120用作目标域待测样本。在 C1→C3，C1→C4，C2→C3，C2→C4，4种情况下对多头自注意力机制经行消融实验，并且取前30次实验结果的平均值作为消融实验结果，结果如表5所示。并且，将算法实时性结果记录在表6中。

表5 消融实验平均识别准确率对比

表6 算法实时性

由表6结果可知，多头注意力机制会增加算法的计算复杂度，从而导致算法的实时性降低。通过表5的消融实验结果可以看出注意力机制对于模型的识别精度有一定的提升，这也进一步证明了本文所提方法的有效性。

4 结束语

本文所提出的CAFTL通过优化域自适应迁移学习网络中的特征迁移损失函数使得源域和目标域样本分布差异最小化，因此它具有较好的域泛化性能，可以适应更多的变工况环境。其次，CAFTL融合了多头自注意力机制，而多头自注意力机制中不同的头可以提取到不同的故障信息，提取到的故障信息越多，就使CAFTL后续提取到的高维特征具有更好的分类性。因CAFTL在域泛化性能和分类性能这两方面的优势，使其在滚动轴承源域和目标域样本概率分布不一致的情况下，依旧能够保持对目标域待测样本较高的故障诊断精度，且其对待测样本的故障诊断精度总是高于典型迁移学习方法所能得到的滚动轴承故障诊断精度。