复杂干扰下的管沟机器人内外环滑模自抗扰控制
傅茂龙,孟 文,孟祥印,杨子镱,罗锦泽
(西南交通大学 机械工程学院,成都 610031)
0 引言
铁路涵洞,公路排水渠和地下城市管网的排水管沟发挥着至关重要的作用,但是排水管沟的维护是一项艰巨且具有挑战性的任务,利用机器人系统可以有效地解决该问题。管沟机器人也是一种轮式移动机器人(WMR,wheeled mobile robot)轮式移动机器人是一种经典的欠驱动系统,一种经典的多输入多输出系统,具有强耦合以及容易受到外界环境干扰的系统参数时变的自动控制系统[1]。精准的控制是机器人完成复杂任务的基础,由于机器人的Brockett约束条件的存在,机器人无法获得连续可微,线性时不变的控制系统[2]。机器人的控制问题一直是近些年来的热门问题,并且也已经取得了一定的成果,目前比较成熟的一些控制方法有:反步法控制[3-4];反步法和模糊PID组合方法[5-6];滑模变结构控制[7-10],模糊控制[11],神经网络控制[12-13],自适应控制[14]等等。然而,上述的这些控制方法,都未考虑轮式移动机器人(WMR)的复杂环境扰动,在实际的隧道管沟环境,隧道管沟机器人有可能受到积水,沉积物以及淤泥等情况,会严重影响到隧道管沟机器人的运动控制性能。
现阶段为了解决上述的问题,出现了一定的鲁棒控制方式:文献[15]提出了一种在打滑状态下的自适应控制,利用(RBF NN)径向基函数,逼近运动过程受到的滑动,建立编队机器人的数学模型,来适应滑动与不滑动的情况。文献[16]针对机器人系统本身的特性,提出具有约束状态以及输入能力有限制的机器人的自适应控制,结合反步法设计出抗饱和的控制方法,针对外界的扰动设计对应的自适应控制律,最终证明了方法的有效性。文献[17]针对的是机器人本身所承受的载荷不确定的情况,采取的是预测控制的方式,整体机器人分为两个控制部分,一部分是离线计算和在线调度的部分,采用极大极小的鲁棒预测控制算法,实现了对于机器人的跟踪控制,证明了方法的有效性。尽管上述的方法能够在一定程度上抑制复杂环境以及机器人本身系统限制带来的影响,也具有相对不错的系统性能,但是上述的控制方式还是存在着一些问题:①自适应控制需要知道扰动的大致范围,但实际情况无法获知;②对于预测控制,需要实时计算更新速度等参量,计算量会比较大。
对于以上的问题,一些相关的学者提出了基于观测的思想,利用观测到的机器人内部扰动以及外界环境扰动,提前对扰动进行抑制,设计出基于扰动观测器的控制律。因其观测器具有其他控制方式不具备的优点,近些年也一直是研究的热点,常用的扰动观测器有:非线性指数扰动观测器;扩张状态观测器[18];慢时变干扰观测器;广义的比例积分观测器;文献[19]提出了一种基于扰动观测器的自适应跟踪控制方法,重点是观测机器人的动力学方程中机器人内部干扰,解决了模型中存在的不确定问题,利用观测值,有效地提高了机器人整体性能。文献[20]提出了一种基于超螺旋干扰观测器的机器人控制方法,首先基于反步法设计运动学控制律,利用超螺旋干扰观测器观测得到的复合干扰,配合设计的非线性滑模控制,取得了不错的抗干扰能了和跟踪性能;文献[1]对比扰动建模与不建模的情况下的轨迹跟踪控制,发现对干扰进行建模后比PID控制器误差更小。文献[21]提出了一种基于扩张状态观测器的线性自抗扰控制,对机器人受到的总扰动进行观测,再利用观测到的总扰动设计对应的ADRC控制器,能够有效的抑制不确定因素对于机器人性能的影响,使得机器人能够准确无误的跟踪上轨迹。
本文提出一种复杂环境干扰下的扩张状态观测器的内外环滑模变结构自抗扰控制方法。首先,把复杂环境干扰解耦成横向与纵向的干扰,在此基础上建立干扰下的管沟机器人的差分运动学模型。依据管沟机器人的运动学模型建立外环滑模变结构控制器,引入非线性微分器,求解出理想的速度与角速度控制律。设计扩张状态观测器估计机器人实际过程中受到的扰动,利用扰动的估计值构建内环的滑模控制器,修正外环的理论角速度与速度控制律。最后利用Lyapunov稳定性原理对闭环系统进行了稳定性分析,同时搭建了Matlab的Simulink仿真实验平台,对比三种不同的控制方法,验证了控制方法的有效性和可靠性。
1 隧道管沟机器人差分驱动模型
如图1所示,隧道管沟机器人左右两侧分别采用一个直流无刷电机进行控制,故物理模型可以进一步简化,如图2所示。
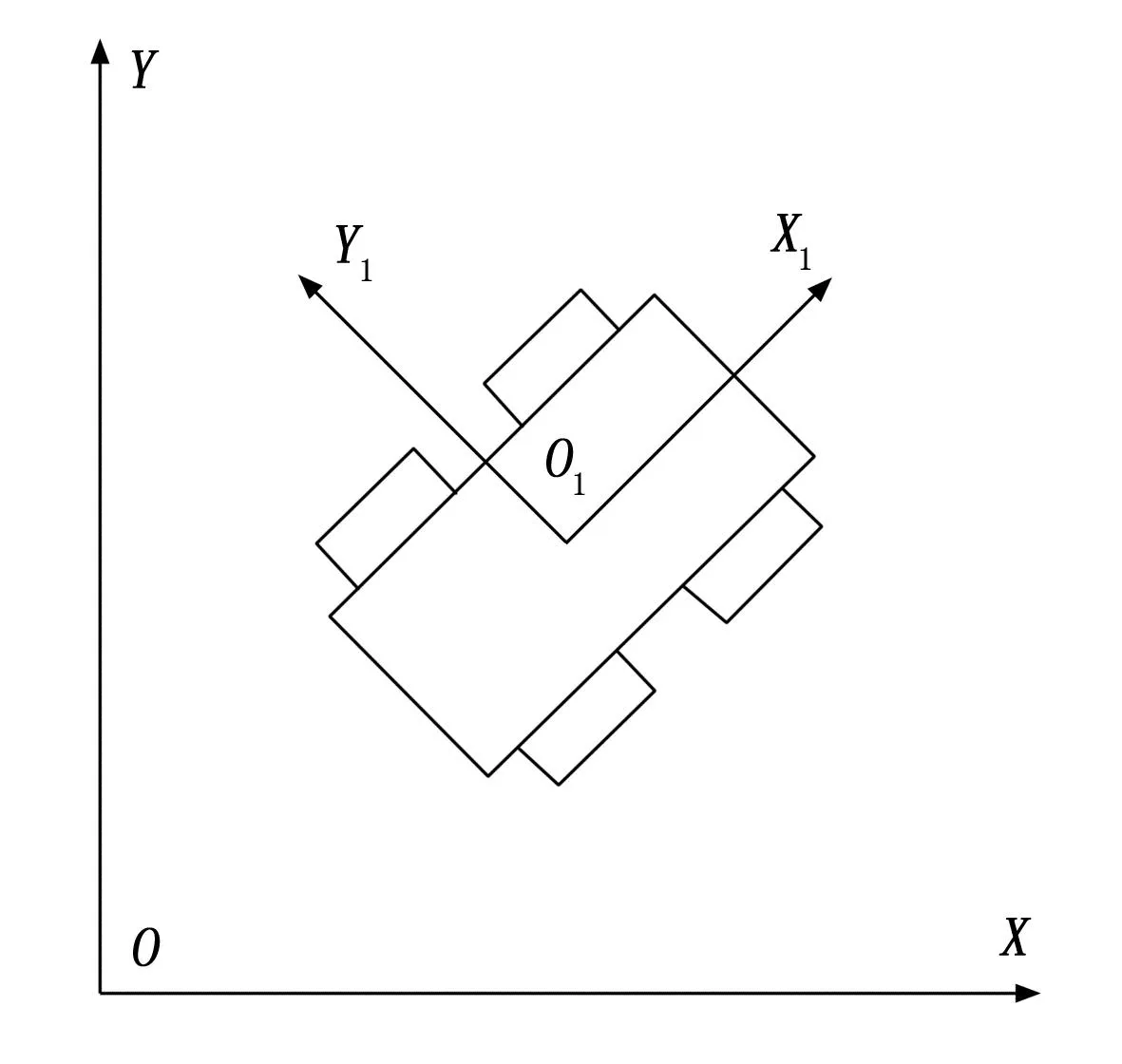
图1 隧道管沟机器人物理模型

图2 隧道管沟机器人简化物理模型
隧道管沟机器人的左右轮的线速度为vl和vr,依据增加复杂环境干扰的物理模型,推出隧道管沟机器人的前进速度与角速度如下:
(1)
依据上述公式以及解耦的复杂环境干扰,推出机器人的运动学方程为:
(2)

2 基于扩张状态观测器的内外环控制系统设计
2.1 外环速度滑模控制器设计

(3)
式中,k1>0,k2>0是滑模面参数。
依据上式,即可推出理想的姿态角θd和速度控制律V如下:
(4)
2.2 外环角速度滑模控制器设计

本文引入一个非线性的微分控制器,因为在求解隧道管沟机器人的角速度控制律时,需要对上式的θd进行求微分,由于求导的过程较为复杂,定义θd=σ1,采用如下的非线性微分器求解:
(5)

(6)
式中,sign是符号切换函数。
定义机器人姿态角的跟踪误差为:θe=θ-θd设定角速度控制器的滑模面为:s3=θe,滑模面的趋近律为:-k5s3-ε1sign(s3),则可以推导角速度的控制律如下:
(7)
式中,k5>0,ε1>0是滑模面的参数。
综上所述,从而保证机器人角速度θ能够快速跟踪上θd。
2.3 扩张状态观测器设计
重新定义机器人的跟踪误差如下:
(8)
结合上述,推导出如下的误差微分方程:
(9)
式中,ux=Vcosθ代表轴的速度输入,uy=Vsinθ代表轴的速度输入,uθ=W代表机器人的角速度输入,dx=Vecosθ+vhsinθ代表轴的干扰,dy=Vesinθ-vhcosθ代表轴的干扰,de=We代表角速度的干扰。
上式中的Ve和We由如下表达式构成:
(10)
依据上述公式,定义x1=ex,x2=dx,y1=ey,y2=dy,θ1=eθ,θ2=dθ设计如下的扩张状态观测器(ESO):
(11)

设计观测器增益参数α1,α3,α5>0,α2,α4,α5<0,β1,β2,β3>0使得观测器系统的根轨迹全部位于复平面的左半边,使得观测器收敛。
2.4 内环滑模变结构控制器设计
(12)
则设计的内环的控制律如下方程所示:
(13)

3 控制系统稳定性分析
3.1 外环滑模控制器稳定性分析
依据上式的速度控制律方程,已知滑模面为s1=xe,s2=ye本小节以x为例子分析外环滑模控制器的稳定性,假定x状态的Lyapunov方程如下所示:
(14)
对Lyapunov方程进行求导,得到如下公式:
(15)

分析θ状态变量的角速度外环滑模控制器的稳定性,依据上式可知滑模面为:s3=θe,定义如下的Lyapunov方程:
(16)
对上式进行求导,可得如下方程:
(17)
式中,sign(s3)为符号函数,当s3≠0时,sign(s3)在接近0的范围内的可以近似看作如下方程:
(18)
式中,ε是一个极小的正数
则对上式的Lyapunov求导结果变为如下:
(19)

3.2 扩张状态观测器稳定性分析
定义如下观测的误差方程:
(20)
依据上述,可以推出如下方程式:
(21)
以下从X轴方向分析观测器的稳定性,Y轴和角速度类似。

(22)
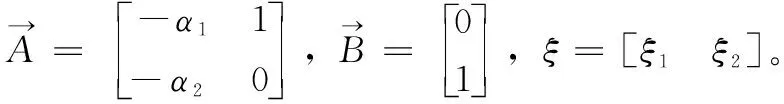
定理1:对于任意给定的对称正定矩阵Q,存在对称正定矩阵P,满足如下的Lyapunov方程[22]:
(23)
则可以定义观测器的Lyapunov方程为:
V(g)=β1ξTPξ
(24)
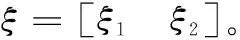
则可以推导出观测器Lyapunov方程导数如下:
(25)
并且有如下关系式:
(26)
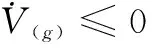
(27)
由上式可知,扩张状态观测器的收敛速度与参数β1有关系,随着β1逐渐变小,观测误差逐渐收敛至0。
3.3 内环滑模变结构控制器稳定性分析
定理2:对于G:[0,∞)∈,不等式方程的解为[23]:

(28)
式中,a为任意的常数。
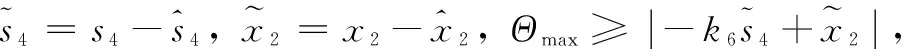
设计滑模面为:s4=x1,由上述可以推出:
(29)
选取Lyapunov函数为:
(30)
则可以推导出如下方程:
(31)
依据上式可以推导出如下方程:
(32)
V(s4)(t)≤e-(2k6-1)(t-t0)V(s4)(t0)+
(33)
当t→∞时,控制系统的收敛速度取决于滑模控制器和扩张状态观测器的参数。选取k6>0.5,可以推出如下公式:
(34)
3.4 闭环控制系统稳定性分析
综合考虑扩张状态观测器与滑模变结构控制器的闭环系统,设闭环系统的Lyapunov函数为:V(q)=V(g)+V(s4),则可以推导出如下方程:
(35)
闭环系统整体收敛速度取决于观测器参数与滑模控制参数,选取合适参数使得闭环系统稳定。以上分析了X轴上x状态的稳定性,剩下的y,θ控制器结构类似,所以稳定性分析方法一致。
4 扩张状态观测器的内外环滑模自抗扰控制方法结构框图
本文设计了一个仿真对比实验,以比较不同控制系统的性能表现。在实验中,使用了三种不同的控制系统,包括:PID控制系统、不加观测器的滑模控制系统以及添加了扩张状态观测器的滑模控制系统。实验的框图如图3所示,其中外环控制器得出理想的速度与角速度控制律,并将这些控制律应用于系统中。同时,扩张状态观测器用于观测系统所受到的扰动,并将其反馈到系统中。内环的控制器通过观测到的扰动值对外环的速度与角速度进行修正,从而保证整个控制系统的稳定性和鲁棒性。具体而言,当系统受到外部扰动时,扩张状态观测器会及时地检测到并反馈到内环的控制器中,从而使控制器能够对速度和角速度进行实时调整,以保证系统的性能表现。通过这样的仿真对比实验,可以评估不同的控制系统的性能表现,验证所提出算法的有效性。

图3 仿真实验框图
5 仿真实验
为了验证本文提出的在复杂环境干扰下使用扩张状态观测器的内外环滑模控制方法的有效性,使用Matlab中的Simulink模块来搭建控制结构框图。在干扰仿真实验中,首先引入不同程度的随机干扰信号,然后对比测试了使用扩张状态观测器的内外环滑模控制方法和传统的PID控制方法在干扰环境下的表现差异,进行仿真实验以验证控制方法的可行性。
本文选取的理想路径为:xd=t,yd=sin(0.5xd)+0.5xd+1,各个控制器模块的参数如表1所示。
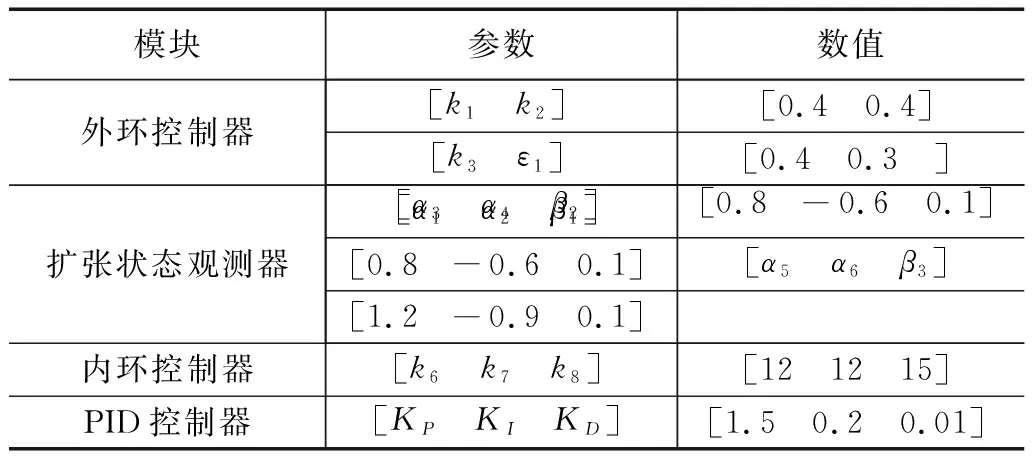
表1 控制器参数
如图4所示,图中展示了扩张状态观测器观测(ESO)的值,ESO将机器人系统的输入和输出作为观测器的输入,得出了对应的状态变量的观测值。可以看到观测器准确的观测出对应状态变量的值,并且具有很好的精度,能够有效的对管沟机器人状态进行监控。

图4 ESO观测器观测状态变量值


图5 管沟机器人状态变量

图6 管沟机器人的实际位置
实验结果分析:
依据上述的实验结果,可以推断出:在这三种不同的控制方式下,管沟机器人都表现出了不错的控制性能。但是因为扩张状态观测器能够实时的观测出机器人受到的干扰,并且配内环的滑模控制器来修正外环的理想控制参量,所以获得了更好的控制精度和性能。并且在仿真实验中,基于扩张状态观测器的内外环滑模自抗扰控制对运动的轨迹和姿态角都获得了不错的控制效果。综上所述,在实际的工作过程中,当机器人的干扰条件和环境发生变化时,设计的控制器依旧能够保持稳定的控制性能,在实际工程环境中使用这种控制算法,可以提高机器人的工作效率和鲁棒性,助力机器人进行管沟巡检作业。
6 结束语
为解决管沟机器人在复杂干扰环境下的运动控制问题,提出了一种基于扩张状态观测器的内外环滑模自抗扰控制方法。首先将复杂环境干扰解耦成横向和纵向的干扰参量,并且在此基础上建立了受干扰的差分驱动运动模型。在受干扰差分运动学模型基础上,建立了外环的滑模变结构控制器,得出理想的速度和角速度控制律。在此同时,建立出机器人系统的扩张状态观测器,利用观测得到的扰动建立出内环的滑模控制器,对外环的控制律进行修正,增强系统的鲁棒性和运动控制精度。
利用Lyapunov稳定性原理分析系统,证明了整个闭环系统的稳定性,确保机器人系统稳定运行。同时在Matlab的Simulink中搭建了三种控制方式的仿真实验,结果表明所设计出的扩张状态观测器的内外环滑模自抗扰控制方法具有更高的运动控制精度和更强的抗干扰性能,能够更好的适应干扰环境下的控制需求。因此,本文设计的控制方法具有较高的工程应用价值和研究意义。

