基于优化故障树模型的机械液压系统原位检测研究

刘博伟，杨佩璇，何广川

(1.重庆医科大学附属第一医院，重庆 400000；2.中国汽车工程研究院股份有限公司，重庆 400000；3.安道拓(重庆)汽车部件有限公司，重庆 400000)

0 引言

液压系统的作用是通过改变压强来增大作用力，因为它具有工作效率高的特点，因此液压系统被广泛地应用于各种工业领域：隧道施工、钢铁、采矿行业、冶金等大型设备，都是以液压系统为主要的动力系统，液压系统产品在我国国民经济的建设中有着举足轻重的作用。当前，液压系统的结构设计日趋复杂，而且使用中对液压系统的作业精度要求逐步提升。由于液压系统的机电一体化程度日趋密切，对液压系统的性能要求也在不断提高，此外由于液压系统是大型设备的主要零部件，对其工作强度和可靠性的要求也在不断增加。尽管机械液压系统在现代机械设备，特别是大型、特大型设备中的应用日益广泛，但是在长期、高强度的作业过程中，由于油液性能的变质或不稳定，以及使用、维护上的不当，液压元件的磨损、生锈等因素，导致机械液压系统的工作效率下降，稳定性变差，进而产生故障现象[1]。机械液压系统是一个封闭的管路循环系统，所以它的故障本身就是一个隐蔽性、变幻性和多元素性的特点，其故障不直观，也不容易检查，这就导致了它出现故障的概率大大提高。

机械液压系统检测是保证系统运行效率与安全性的重要手段，为保证故障检测工作不会对机械液压系统内部结构产生影响，同时保证检测精度，提出机械液压系统原位检测方法。原位检测就是在不破坏或微破坏目标的前提下获取检测结果的过程，目前发展较为成熟的机械液压系统检测方法包括：基于DSP(digital signal processor，数字信号处理技术)的故障检测方法[2]、基于大数据分析的液压系统故障检测方法[3]，以及基于BP(back propagation，反向传播)人工神经网络的液压系统故障检测方法[4]，然而上述检测方法需要将相关的硬件设备安装到机械液压系统内部，因此需要在一定程度上破坏机械液压系统结构，从上述传统方法工作中的运行输出情况来看，存在明显的检测误差问题，进而导致了系统故障风险的增加。针对传统机械液压系统复位检测算法存在的各种问题，引入优化故障树模型，对液压系统的故障特征进行系统识别。优化故障树模型是用事件符号、逻辑门符号、过渡符号来刻画不同事件间的因果关系。利用优化故障树模型对机械液压系统原位检测方法进行优化设计，以期能够在不影响机械液压系统结构的情况下，提升系统的检测精度。

1 机械液压系统原位检测方法设计

优化设计的机械液压系统原位检测方法的基本原理是根据机械液压系统的工作原理，综合考虑故障发生位置、信号可采集度等多个因素，设置原位检测的测点位置，且保证设置的测点位置均分布在机械液压系统表面。在测点位置上收集机械液压系统的实时运行数据，利用构建的优化故障树模型确定当前系统是否处于故障状态，并将故障位置、流量、振动、泄漏量、温度等参数检测结果以可视化的形式输出，实现机械液压系统的原位检测任务，如果检测系统识别出液压系统复位存在问题，会发出报警信号提醒工作人员及时检修系统设备。

1.1 模拟机械液压系统运行过程

从液压系统的组成结构方面来考虑，一个常规的且具有代表性的机械液压系统由动力元件、执行元件、控制元件、辅助元件和液压油五个部分组成，具体的系统运行原理如图1所示。

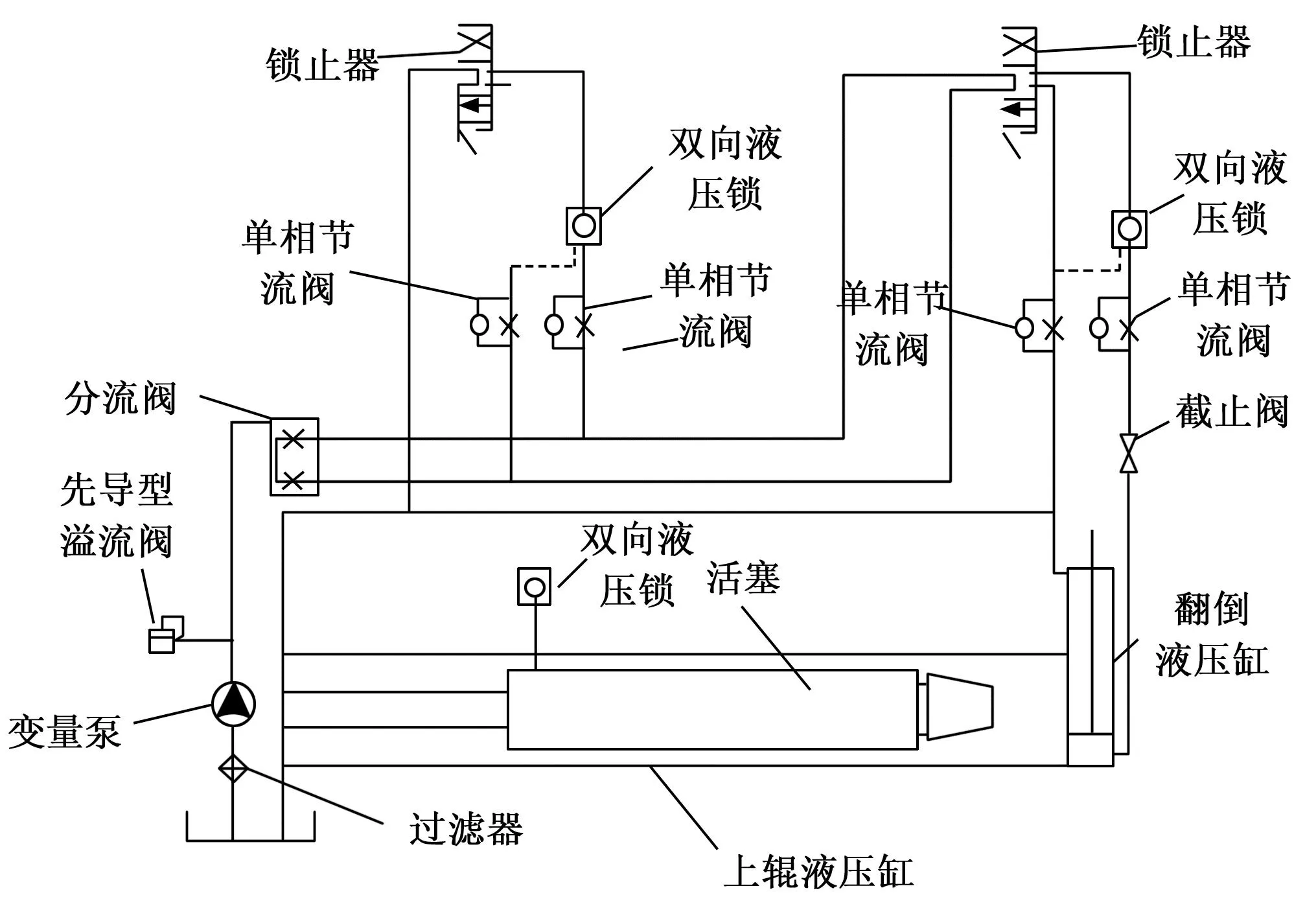
图1 机械液压系统工作原理图

图1中过滤器、油管、油箱以及密封装置均为液压辅助元件，变量泵、齿轮泵、叶片泵为液压动力元件，上辊液压缸和翻倒液压泵均为液压执行元件，而溢流阀、调压阀、分流阀、截止阀、换向阀等均为液压控制元件。机械液压系统在实际运行过程中，液压油经变速泵输送，通过减压阀及遥控调压阀对上辊的升压及下压进行分步调整，实现了对上辊的升压及上辊的降压。然后油道分成两部分，一部分进入翻车机系统，另一股则通过转向阀流入到提升系统中。两个子系统具体包括了控制阀和液压缸，液压缸通过叠加阀组进行控制，每组叠加阀包括了电磁换向阀、节流阀和液控单向阀。升降机构主要实现上辊的升降，上辊的升降执行机构为上辊两端两个并列的液压缸。上辊下压为工作过程，匀速下降过程要求速度较慢，由于上辊以及活塞杆的质量较大，因此要求回油管路有较大背压。当上辊筒与工料接触时，由于压力的突然上升，使油缸内的油压迅速上升到最高值。在加压完成后，上辊迅速、匀速地上升，液压缸中的油压可以克服上辊和活塞杆的重力，使油压的数值小于加压时的压力。液压附件和导管会发生一定程度的弹性变形，可以把液压导管看成一个承受内部压力的薄壳物体，并在理论上进行计算。在液压系统的内部作用下，液压系统管道的轴向应力与压力之间的关系系数σ表示为：

(1)

式中，变量F为机械液压系统中液压油的压力，E、l和rconduit分别为系统导管的弹性模量、壁厚和平均半径。在系统执行状态下，运送液压油导管的轴向应变与承受的内压之间存在正相关关系[5]。按照机械液压系统的工作原理，各模块会根据机械元件的驱动需求和工作指令，将相应的液压油输入到系统中。考虑各个液压控制元件的工作状态和最大耐受度，确定最终系统输出的液压大小，由此完成对机械液压系统工作流程的模拟。

1.2 设置机械液压系统原位检测点

受到机械液压系统导管性质的影响，当导管内液压油压力过大并高于导管的弹性极限时，会在导管表面产生泄漏点，从而产生系统故障。通常情况下导管弹性会实现设定一个阈值，但由于液压系统长期在高温高压环境下工作，或由于长时间未更换油液而导致液压系统油液变质，会导致系统阈值范围被突破进而引发突变性故障[6]。在已知起始测点位置的情况下，任意测点位置的设置情况可以表示为：

w(i)=w(0)+d×(i-0)

(2)

其中：w(0)和w(i)分别表示的是起始测点和第i个测点的位置设置情况，d为任意两个测点之间的间距[7]。将两种类型的测点设置结果进行融合，得出机械液压系统原位检测测点的最终设置结果。测试点的位置选择和测量点之间的距离都具有一定的随机性，选择任意一个测试点都不会影响最终的测试结果。

1.3 机械液压系统故障状态的确定

以机械液压系统实时运行数据为研究对象，利用优化故障树模型，分析运行数据与故障状态之间的逻辑关系，进而判断出当前机械液压系统是否处于异常状态或故障状态[8]。在故障状态检测的环节，如图2所示当液压系统发生故障时，液压油流动方向会发生偏差，同时反射角度β也会发生变化，导致液压站i点的液压值与标准值产生较大偏差。首先利用图2表示原理，在不破坏液压系统破坏系统的前提下，采集机械液压系统的实时运行数据，监测系统的内部液压结构的运行状态和压力状态。

图2 机械液压系统原位数据采集原理图

按照图2表示原理，可以得出机械液压系统任意监测点位置i处的液压值xHydraulic value，具体的采集结果如下所示：

xHydraulic value=u×Acosβ

(3)

式中，u表示测量传感器输出信号的传输路径长度矢量，β表示测量信号在机械液压系统中的反射角度，A为液压系统有效截面积，该变量的计算公式为：

(4)

式中，变量r为液压系统有效导管半径，将公式(4)的计算结果代入到公式(3)中，即可得出普通监测点位置上液压值数据的采集结果，并根据测量的结果判断液压系统的液位是否已经出现了异常。若测点位置处于液压控制元件位置上，则变量r的取值为液压控制元件的有效活塞半径[9]。按照上述计算方法，可以得出机械液压系统中其他运行数据的采集结果，将其标记为X，并以此作为优化故障树模型的输入项。在机械液压系统故障状态检测过程中，首先根据机械液压系统可能存在的故障类型构建相应的优化故障树模型，构建结果如图3所示。

图3 机械液压系统的优化故障树模型示意图

将图3中表示的机械液压系统优化故障树模型的结构函数表示为：

T(X)=T(x1，x2…xn)

(5)

式中，x1，x2…xn为机械液压系统运行数据的采集结果，在此基础上对公式(5)进行分解、数学期望等操作，得出机械液压系统的分布函数为：

ffault(i)=E(T(xi))

(6)

式中，变量E()为数学期望函数，将公式(5)的计算结果代入到公式(6)中，即可得出机械液压系统分布函数求解结果[10]。机械液压系统优化故障树模型的分析可以分为定性分析和定量分析两个部分，定性分析就是求出故障树的全部最小割集和最小径集。割集是一组发生在错误树中的基本事件。当一个事件集中的多个事件在同一时间内同时出现，且其顶点一定会出现，这个事件集中称为割集；如果在一个割集中去除了任何底部的一个，顶部的一个没有出现，这个切割集叫做最小切割集。即割集中含有一个最小割集中，而这个最小割集中的任何一个底层事件都不能再得到它。如果出现了最小割集，那么就一定会出现顶事件[11]。定量分析的重点在于从底部事件的出现概率出发，进而推演顶部事件的出现概率，并对底部事件的故障概率进行计算。在此基础上，对顶事件进行安全性的量化评估。从图3中可以看出，机械液压系统状态为顶事件，节流阀失效、溢流阀失效、过滤器失效等事件为底事件，在机械液压系统故障状态检测过程中，本事件的发生概率取决于优化故障树模型的结构和各类事件的发生概率[12]。底事件的发生概率可以表示为：

λbottom(i，t)=1-e-μt

(7)

其中：t为机械液压系统运行的时间，μ为系统底事件i引起的失效率[13]。按照上述方式可以得出图3表示优化故障树模型中所有底事件发生概率的求解结果，在此基础上，得出顶事件发生故障的概率求解结果为：

(8)

式中，nevent表示优化故障树模型中的底事件数量，通过公式(7)和公式(8)的联立，即可得出机械液压系统故障概率的求解结果，若计算得出λtop(t)的值高于0.9，则说明t时刻机械液压系统处于故障状态，否则认为当前机械液压系统处于正常运行状态，重复上述操作完成对机械液压系统故障状态的检测任务。优化故障树模型的优势表现在，一方面，通过运行时间、系统失效率和事件触发概率的计算，相对准确地评估出系统出现故障的风险。故障树的复杂程度和在运算中的迭代次数都会影响到故障树功能和参数优化效果；另一方面优化故障树模型在不同故障类型的分类识别方面，相对于其他机器学习和神经网络算法具有一定优势，因为故障数据模型可以在无监督环境下，实现对液压故障状态和故障类型的推理。

1.4 计算机械液压系统原位检测参数

机械液压系统的运行过程较为复杂，会受到各种参数和系统状态的影响，其中机械液压的核心参数包括：系统流量、液压泄漏量、液压值、振动烈度等，作为机械液压系统的原位检测参数，其中系统流量参数的原位检测结果为：

(9)

式中，κflow和Arestrictor分别为流量系数和节流器孔的过流面积，ρ为机械液压系统中的油液密度，ΔP对应的是系统中节流器的前后压差[14]。另外，机械液压系统液压泄漏量和振动烈度参数的检测结果为：

(10)

其中：hgap为系统泄露点位置上的间隙高度，υ和dplunger分别为柱塞运动速度和直径，Nvibrate为机械液压系统振动信号样本数量，vvibrate(i)表示第i个振动速度信号的离散值。按照上述计算方式，可以得出机械液压系统中所有测点位置上相关参数的原位检测结果，将各种参数：系统流量、液压泄漏量、液压值、振动烈度的实时测量值都作为输入项，输入优化故障树模型，通过模型的分类判断和综合分析，评估机械液压系统产生故障的风险。

1.5 实现机械液压系统原位检测

机械液压系统原位检测的最终目的，是判断当前机械液压系统是否存在故障现象，并确定故障类型与故障位置，为机械液压系统的维修提供有效参考。通过优化故障树模型的运行，可以直接得出机械液压系统故障状态的检测结果，而故障类型的检测需要利用系统故障参数的检测结果，比对当前参数与不同类型故障下参数范围的重合度[15]。机械液压系统的故障类型包括：液压泵故障、液压系统泄漏故障、液压阀故障、液压缸故障等，根据不同故障类型的作用机理，确定故障参数的运行范围，并利用公式(11)计算当前参数与任意故障类型j之间的匹配度。

(11)

其中：φ和φstandard(j)为机械液压系统原位检测参数的综合计算结果和故障类型j的标准参数运行范围，变量φ的求解公式为：

φ=W⊗Wleakage⊗ψ

(12)

若公式(11)得出的计算结果s(j)高于阈值s0，则说明当前机械液压系统的故障类型为j，否则需要更换故障匹配类型对象，直至满足阈值条件为止。机械液压系统泄漏量最大值对应的检测点即为故障位置的检测结果，最终将故障状态、参数、类型、位置等检测结果以可视化的形式输出，完成机械液压系统的原位检测工作。优化故障树模型还能够根据对故障数据的分析和参数阈值区间的判断，识别出机械液压系统所产生的故障类型，以便于更准确地对故障点位置和故障的严重程度进行判断。

2 原位检测性能测试实验分析

2.1 实验准备

本次实验选择塔式起重机中的机械液压系统作为检测对象，该系统中的液压油由液压泵输送至装置内的制动器，而液压泵则是通过引擎或电动机来驱动的。通过操作不同的液压控制阀来获得所需的压力或流量。每个液压元件通过液压管路连接起来。此次实验中选择的机械液压系统由动力元件、控制元件和执行元件三个部分组成，其中动力元件为柱塞油泵，控制元件包括溢流阀、单向阀、节流阀等元件，执行元件为液压马达。机械液压系统在起动、加速、快近阶段的机械负载分别为6 200 N、4 700 N和3 000 N，系统内部各元件之间的摩擦系数均为0.15。通过对多个指令动作的评估，能够更全面地模拟机械液压系统的真实工作状态，并从融合视角综合判断机械液压系统的工作稳定性和可靠性。在选择的机械液压系统表面安装检测装置，检测装置主要是将实际的液压信号转化为电信号，受检测装置自身结构的制约，其输出的电信号往往比较弱，且含有很多噪声，这就要求信号调整器对其进行适当的调理[16]。而检测装置则是将经调理后的模拟信号转换为数字信号，方便计算机读取与分析，但当信噪比值持续降低时并突破阈值后，只能够通过适当调整传感器之间的距离，并通过判决再生的方法，生成一组干扰性较小的模拟信号。图4表示的是机械液压系统原位检测设备的安装实景。

图4 机械液压系统原位检测设备安装实景

机械液压系统中装设的检测装置主要包括压力传感器[17]、流量传感器[18]等，其中压力传感器型号为PH102，该传感器具有很好的防水功能，它有良好的抗震功能，测量精度为0.5%FS，输出信号强度为16 dMb。流量传感器的传感器选择了涡轮流量传感器，该传感器使用了无接触探测器，能够对暂态和脉动两种流量进行探测。其测量准确度为0.25%，该传感器是一种用来对液压系统中的油口进行流量测量的传感器。传感器的安装必须与机械液压系统的构造方式相匹配。从管道连接的角度出发，将传感器置于系统表面，分别采用并联与串联两种形式[19-20]，在安装上可采用增加转接点或阀块的方法。检测设备安装完成后，将其与供电电源相连，判断检测设备是否能够成功输出系统运行信号，从而完成对检测设备的调试工作。采用人为控制的方式设定机械液压系统的运行工况，为保证实验的可操作性，将机械液压系统的运行状态始终设定为故障状态，但故障类型、故障位置存在差别。为保证实验结果的可信度，此次实验共设置50组工况，其中部分工况的设定情况如表1所示。

表1 机械液压系统运行工况设定数据表

按照上述方式可以得出实验中所有工况的设定结果，表1中液压值、液压油流量和泄漏量为不同工况下机械液压系统的真实值，以此作为判断机械液压系统检测精度的比对标准。机械液压系统产生的故障点不限于同一位置，例如，柱塞泵、齿轮泵、溢流阀、换向阀和液压缸都可能出现故障，或几种零部件混合故障，检测难度极大，这与机械液压泵的结构设计复杂程度相关。基于优化故障树模型判断故障，就是要通过多个树状结果和节点分裂模式，辨别多故障的形态，进行提升对不同的复杂故障类型判定准确率。

2.2 实验结果与分析

选择SNIP工具作为机械液压系统原位检测方法中的优化故障树模型的生成工具，该工具采用了Linux环境下的QT技术进行开发，并通过Graphviz技术对系统特性进行了建模，并对故障树进行了可视化展示。实验中设置的对比检测方法为：基于DSP的故障检测方法和基于大数据分析的液压系统故障检测方法，在相同的实验环境下完成对比检测方法的开发与运行，并得出相应的检测结果。根据实验目的，分别从检测精度性能和检测破坏程度两个方面设置量化测试指标，其中检测精度性能的测试指标为液压值、液压油流量和泄漏量参数检测误差，上述指标的数值结果为：

(13)

式中，Wdetection、Wleakage-detection和ψdetection分别为液压值、液压油流量和泄漏量参数的检测结果，Wsetting、Wleakage-setting和ψsetting为液压值、液压油流量和泄漏量参数的设定值。最终计算得出参数检测误差越小，证明对应方法的检测精度越高。另外，检测破坏程度性能的测试指标的测试结果为：

ζ=ξInternal deviation+ξwear and tear

(14)

式中，ξInternal deviation和ξwear and tear分别为内部结构偏差量与内部磨损量。公式(14)的计算结果ζ取值越小，说明检测方法对机械液压系统的破坏程度越小。通过机械液压系统原位检测输出结果数据的统计，得出反映系统检测精度性能的测试结果，如表2所示。

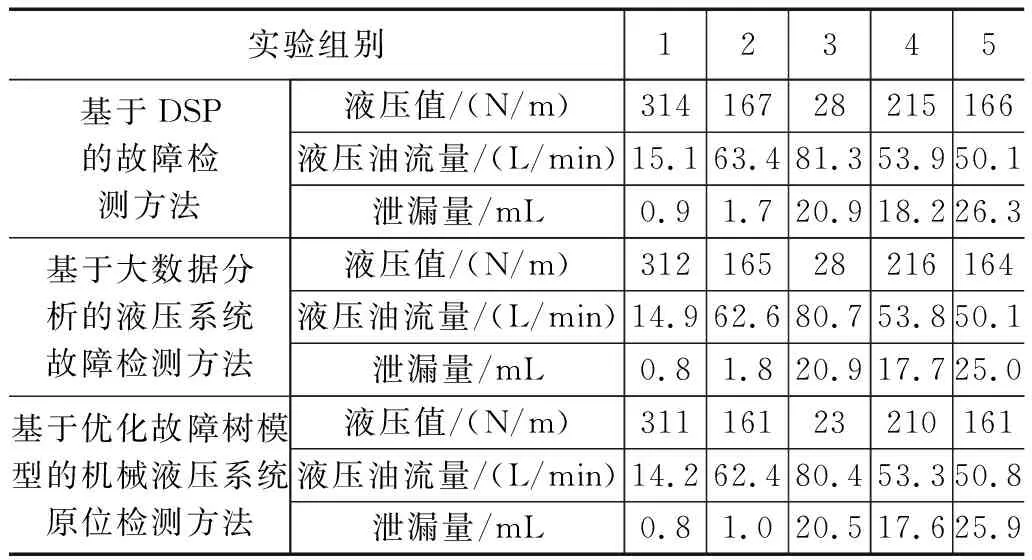
表2 机械液压系统原位检测精度性能测试数据表

将表1和表2中的数据代入到公式(13)中，计算得出基于DSP的故障检测方法对液压值、液压油流量和泄漏量参数的平均检测误差分别为5.6 N/m、0.76 L/min和0.56 mL，基于大数据分析的液压系统故障检测方法得出的参数检测误差的平均值为4.6 N/m、0.42 L/min和0.48 mL，而优化设计方法输出的平均参数检测误差分别为0.8 N/m、0.18 L/min和0.16 mL。另外，通过公式(14)的计算得出三种检测方法对系统破坏程度性能的测试结果，如图5所示。

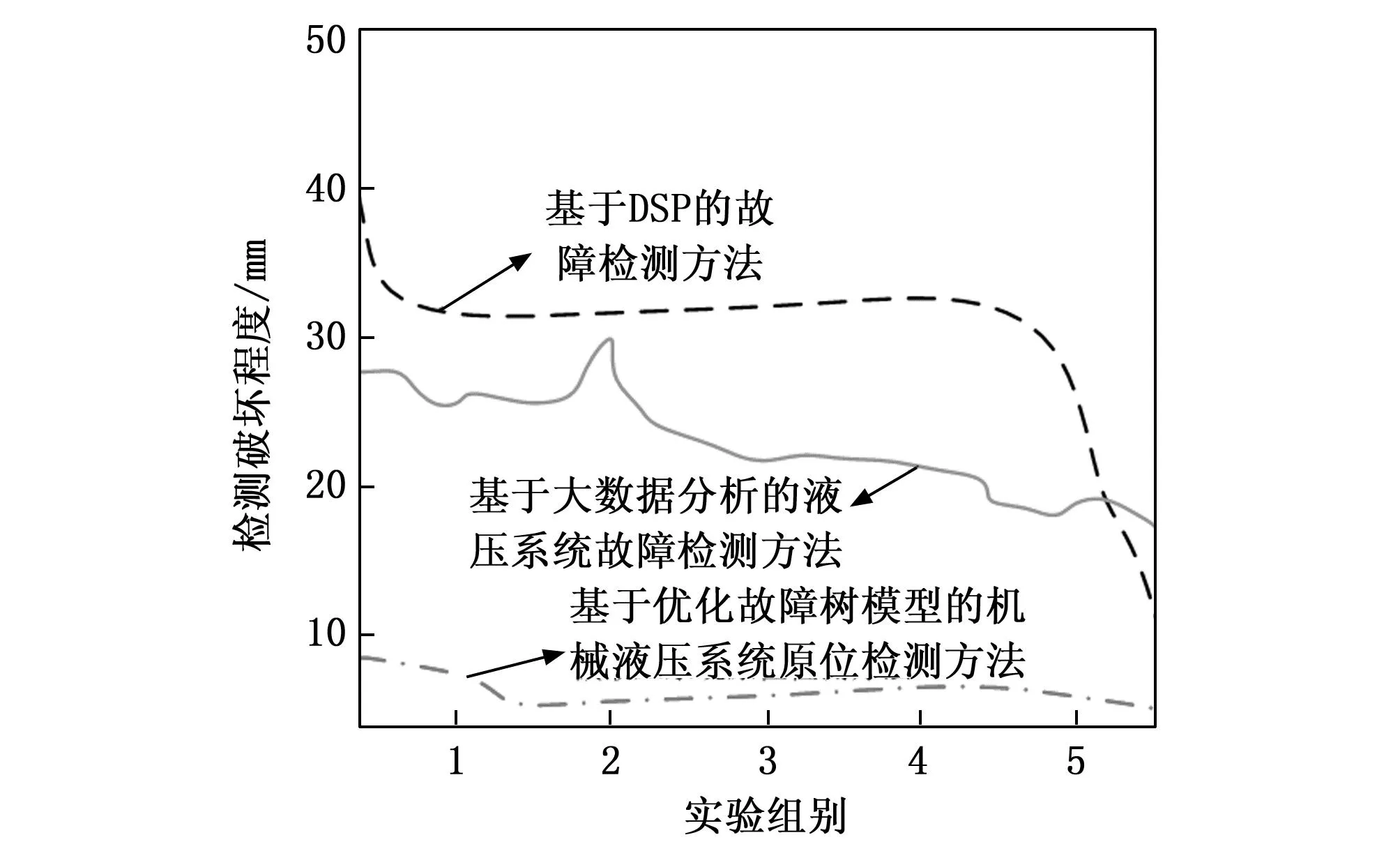
图5 原位检测对机械液压系统破坏程度的测试结果

从图5中可以直观地看出，与两种传统检测方法相比，优化设计检测方法对机械液压系统的破坏程度更小，且低于10 mm，因此满足系统原位检测的要求。

3 结束语

优化故障树模型在安全工程和可靠性工程的领域中有较为广泛的应用，它可以用来分析系统产生失效的各种原因，并找出最好的方法来降低系统性风险。在此次研究中，将优化故障树模型应用到机械液压系统原位检测工作中，能够在不破坏机械液压系统内部结构的情况下，实现对系统的精准检测，为系统的维修工作提供有效参考，间接地提高机械液压系统的运行稳定性。