低真空管道磁浮系统环境测试与数据处理

杨子镱，孟 文，孟祥印，傅茂龙

(西南交通大学 机械工程学院，成都 610031)

0 引言

中国轨道交通的建设和发展是推动经济和提高民生的重要一环，现如今我国的高铁通车总里程已经稳居世界第一，拥有自主知识产权的高速列车核心技术与制造装备也处于世界领先的水平，预计到2035年，我国铁路网总规模将达到20万公里[1]。目前，我国已把满足更严格设计标准下提高车辆运行速度，降低寿命周期成本以及能耗，降低车辆振动和噪声等问题作为下一代高速列车的设计目标[2-3]。由于空气阻力与速度的平方成正比[4]，空气阻力随着速度的增加而变大，与此同时占总阻力的比重也更大，地面接触式列车极限速度只有约400 km/h[5-7]，当时速超过400 km，空气阻力占比将达到所有阻力的80%以上，且会产生更大的气动噪声。在这样的背景下，低真空管道磁浮交通在采用磁悬浮技术的同时，通过在由抽气而接近真空的管道中运行来降低空气阻力和气动噪声，达到了传统轨道交通无法做到的效果，在未来具有广阔的发展前景。

世界各地为发展和改进真空管道磁浮交通运输系统搭建了许多试验系统来进行试验。2013年，埃隆·马斯克(Elon Musk)于美国提出了Hyperloop的概念，它由胶囊车厢、真空管道、推进系统、路线四部分组成，并于2016年首次在户外测试成功[8]。2017年，美国公司Hyperloop One采用永磁电动磁浮的方式搭建完成了实现时速387公里的真空管道运输试验线[9]。2019年，荷兰高铁公司Hardt Hyperloop开发了一套真空管道运输全尺寸试验线。2014年，西南交通大学研究团队将真空管道交通和高温超导钉扎悬浮相融合，完成了全世界第一套集牵引、悬浮、导向以及通信于一体的超导钉扎磁浮-真空管道试验系统“Super-Maglev”[10-11]，该系统线路总长为45 m，弯道半径为6 m，当列车悬浮高度为20 mm时可承载300 kg，并于2018年开始搭建时速可达400公里的真空管道高温超导磁悬浮高速试验平台[12]。

目前，国内外对低真空管道磁浮交通运输系统的数据采集与处理研究较少，并且并未对低真空磁浮系统固有的低真空和磁场环境是否会对系统内传感器检测产生影响进行测试，也未对低真空管道磁浮交通系统数据处理进行研究。通过试验获得的数据要尽可能的反映系统的真实状态，系统内传感器等设备需要在不受环境影响的情况下实现满足测量误差的数据采集。同时，系统是在特殊环境下进行试验测试，列车模型在进行动态测试时数据处理中心采集到的数据因为各种原因会存在异常，这些异常对真实数据的获取、数据可视化与后续数据的相关应用与研究造成干扰。而低真空管道磁浮系统运行重复难度大，试验代价高，因此需要尽可能的减少试验时的干扰，并从每次试验得到的存在各种干扰的数据中尽可能的提取更多的有效信息。为借助低真空管道磁浮系统进行相关动力学、空气动力学、悬浮与导向等基础科学问题与共性关键技术研究，通过有效的试验系统进行大量试验，精准掌握真空管道磁浮系统在静态和动态工作时众多物理量的真实数据是至关重要的，本文针对低真空管道磁浮动模系统进行环境测试和数据处理，实现数据的精准采集、传输和处理，为低真空管道磁浮交通运输相关研究以及设计提供重要可靠的试验手段。首先采用合适的时钟同步方式对各采集节点进行同步触发，保证数据在采集开始时刻的配准；对部分传感器进行真空度与电磁场影响测试；最后以激光位移传感器为例进行了必要的数据处理方式，从噪声环境中得到最有效的数据，并对数据在特殊试验环境下产生的异常值误差进行剔除，降低系统内各设备本身与环境影响造成的数据误差。低真空管道磁浮系统现场环境如图1所示。

图1 低真空管道磁浮系统环境

1 系统功能需求与结构

整个低真空管道磁浮系统总长高于1 600 m，主要包括采集与测试系统、低真空管道本体、真空产生与维持系统、动模系统(列车模型)、悬浮导向系统、牵引与制动系统等。其中低真空管道本体、真空产生与维持系统用于交通运输系统所需低真空环境的产生与动模运行线路的建立；悬浮导向系统、牵引与制动系统用于实现动模的高速运行和制动；采集与处理系统进行试验过程中的数据采集、传输，同时进行相应的处理。主要针对低真空管道磁浮系统的采集与测试系统进行设计与研究。为实现例如真空管道超高速列车空气动力学、管道—桥墩—列车耦合动力学行为等，系统需要对车体悬浮高度、横向位移、温度、管道振动以及形变等众多物理量进行采集测试。

另外，为了可以保证列车模型运行不受影响，车载数据通过WIFI传输到附近无线网络信号接收点，再由以太网传输至监控中心，同时为了使各采集节点进行同步触发采集，采用了GPS+IEEE1588以太网时钟同步的方案：首先通过GPS信号转发模块将外部GPS信号引入管内，车载系统与地面系统通过GPS信号进行主时钟同步，子系统内部通过以太网实现采集节点的IEEE1588同步[13-14]。系统总体框架如图2所示。在实际时钟同步过程中，存在两个主要影响精度的因素：

图2 系统总体框架

1)传播延时：IEEE1588时钟同步主要受到往返报文通讯路径不对称的影响。对于实际的工作情况来说，主从时钟之间的传播延时是不对等的，在本系统中，主从时钟设备之间的报文传输为同一以太网线路，同时打上时间戳是通过在物理层和数据链路层之间添加硬件实现的，因此已经将影响误差降低至可接受的范围。

2)时钟源精度：每个子系统的主时钟均使用自己的参考时钟源，参考时钟源之间的频率偏差和频率波动会影响到子系统之间的时钟同步精度。本系统采用卫星信号转发器将外部GPS信号引入低真空管道内部，通过高精度授时的方式保证子系统之间主时钟达到时钟同步，子系统内部通过IEEE1588协议保证了时钟同步，因此也已经将参考时钟源误差降至最低。

低真空管道是可以产生低真空环境和承载动模以及各种设备的系统，包括了准备段、低真空管道、过渡舱、真空隔离舱门、牵引与制动系统电机支承平台、电机支架、各种进出管道接口、辅助设施支撑等，真空的产生和维持系统与真空管道系统相连，可在24小时内产生极限为0.5 kPa的真空度环境。动模通过牵引与制动系统驱动电机动子实现运行，牵引与制动系统包括直线电机定子(含线圈及铁芯)及动子、储能系统、驱动电源、位置检测及相应的运行控制系统。其中定子、位置检测设备安装在电机支架上，动子与动模相连并安装在两定子之间，动模的运动依靠动子的运动完成。考虑到低真空管道的真空度环境和牵引与制动系统周围产生的磁场可能会对系统内传感器等设备造成测量影响，仅通过选择合适的传感器和设备以及合理布设无法满足一套特殊环境下的精密数据采集与处理要求，需要对所系统内使用到的关键设备进行相关影响分析，各类传感器组成材料或检测原理可能受到低真空环境的影响，以及传感器作为电子设备可能受到牵引与制动系统直线电机通电后磁场的影响，对传感器的环境影响检测是必不可少的。

由于无法多次直接对低真空管道磁浮动模系统抽取真空和直线电机通电操作进行多次环境影响测试，采用设计试验的方法完成环境影响测试。对于真空度影响采用真空泵和真空箱设定真空度为90 kPa进行试验。将被测传感器与采集仪连接并放入真空箱内，同时将采集仪设置为离线采样模式，通过安全扣锁紧使真空箱密闭，被测传感器经过箱内由正常大气环境到真空度为90 kPa的环境并保持放置于该气压一段时间。系统车载测试系统中采用激光位移传感器型号为MLD22-35 V，技术规格如表1所示。

表1 激光位移传感器参数表

通过采集仪设置激光位移传感器采集频率为1 000 Hz，正常环境下测试得到整个过程中测量值服从正态分布，且在传感器测量精度范围内，传感器测量值正常。通过上述实验方法将激光位移传感器和采集仪连接并放置于真空箱内，通过安全扣将真空箱进行密封，再通过真空管将真空箱出气阀和真空泵抽气口进行连接，达到需要的真空环境后关闭真空箱出气阀，使真空箱处于完全密封状态。对真空箱进行抽真空实验并采集位移数据，在经过大约52秒后，真空箱真空度为90 kPa，完成实验后观察数据如图3所示。

图3 抽真空阶段数据变化趋势

在抽取真空过程中，激光位移传感器测量值出现较大的波动现象，整体出现测量值减小的趋势。根据方差计算公式：

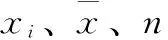
表2 抽真空前后数据对比

由表2可知，抽取到真空环境为90 kPa前后数据测量值减少量最小约为0.023 mm，最大约为0.044 mm。当真空箱内真空度达到90 kPa时，缓慢变化到55 kPa，再通过真空泵快速抽气变回到90 kPa，以此循环多次，采集到的数据如图4所示。

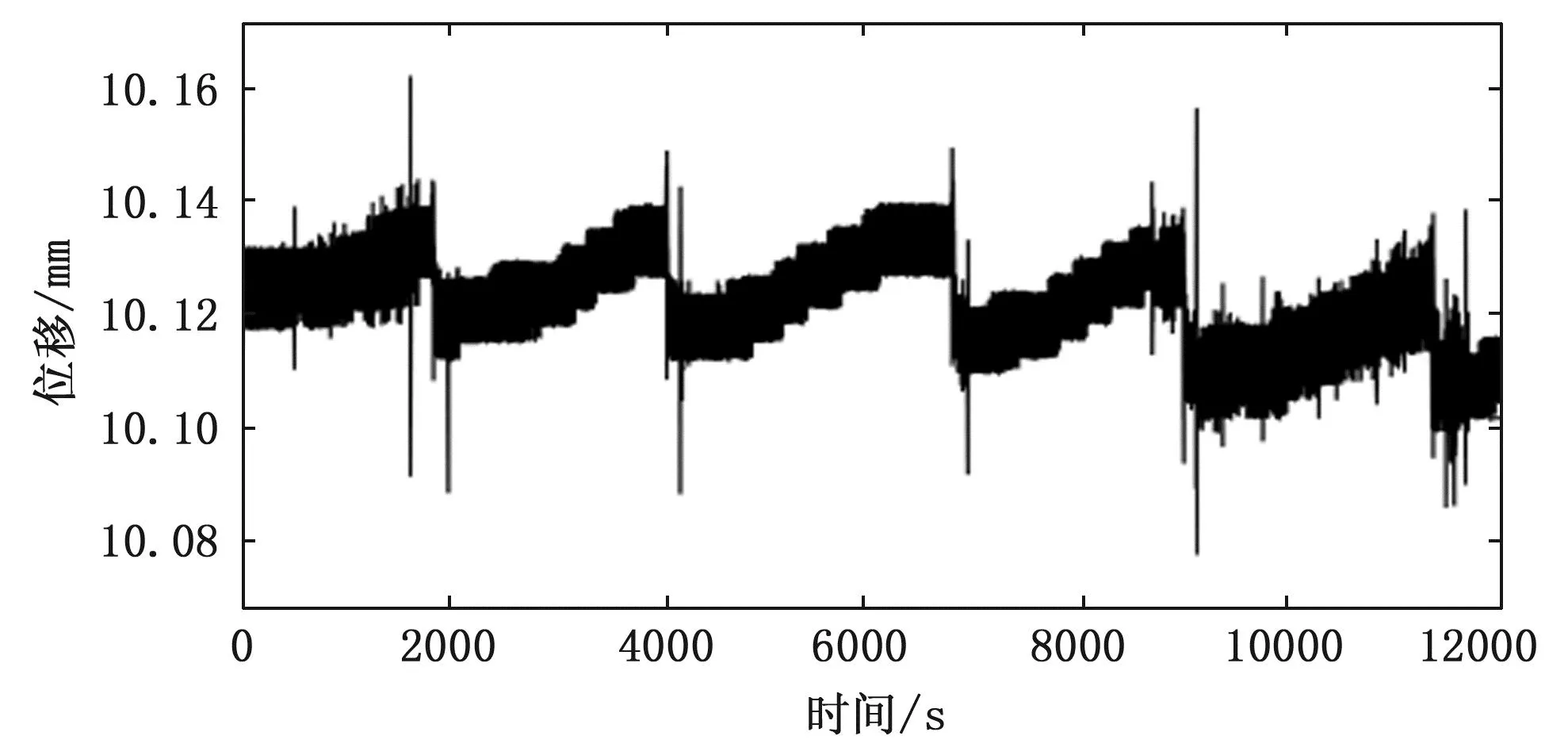
图4 真空度多次变化下激光位移传感器采集的数据

在这5次真空度变化中，测量的位移值变化分别为0.023 3 mm、0.023 1 mm、0.022 7 mm、0.031 3 mm和0.014 5 mm，位移值的变化与真空度的改变并不存在明显的线性关系，但可以发现真空度大小的变化对激光位移传感器的测量值产生了一定的影响，当真空度变大时，激光位移传感器测量值将变小，多次实验得到测量值减少范围为0.014 5～0.043 7 mm。

对比图5绝压90 kPa的稳压状态下噪声情况和图6真空度变化状态下噪声情况可以看出，当激光位移传感器在真空度变化的环境下，测量值受到的噪声影响更大，进一步说明了真空度对激光位移传感器测量值存在影响。

图5 绝压90 kPa的稳压状态下噪声情况

图6 真空度变化状态下噪声情况

在对其他类型传感器(如风速传感器、应变片、三向加速度传感器等)进行相同测量时并未发现受到真空度的影响，抽取真空前后并无差异，且抽取完成前后数据平均值和方差几乎相同。

系统距离牵引与制动系统最近的为车载系统上测量列车模型运行状态的传感器，经测试得到安装位置磁场约为0.010 7 tesla。采用电磁铁通电产生磁场，通过磁场检测仪确定磁场大小后进行相关测试。通过24 V直流电源给电磁铁线圈通电，磁场检测器检测电磁铁线圈周围磁场大小，当电磁铁线圈附近磁场强度达到0.03 T，比实验要求的0.010 7 T更大，在该环境下将传感器紧贴安置于电磁铁表面，在正常情况下进行一段时间测量后给电磁铁线圈通电并保持一段时间，通过采集到的数据观察是否会受到0.03 T以下磁场强度的环境。经测量发现0.03 T磁场强度的环境对系统所选传感器(激光位移传感器、风速传感器、应变片、三向加速度传感器等)均不会产生影响，同时计算得到电磁铁线圈通电前后，所有传感器测量值平均值以及方差基本上相同。

2 数据处理

2.1 数据降噪方法

低真空管道磁浮系统的动态测试存在数据采集环境干扰大，重复成本高等问题，需要尽可能的从存在异常的数据中保留更多的有效信息。考虑到系统传感器种类与数量众多可能导致的设备异常，系统本身构成的复杂性以及动模在实际运行过程中状态的多样性，采集到的信号数据中会出现各种随机噪声，导致后续无法正确处理信号[15]。为达到系统数据采集与测试系统要求的精度，需要对不同程度随机噪声进行有效的降噪处理。对数据噪声的降噪处理可采用以下几种方式。

2.1.1 滑动平均算法

滑动窗口平均法是信息时域处理时的一种常用滤波器，其原理简单且广泛应用于工程实际之中。滑动窗口平均法是一种低通滤波器，主要可用于数据的平滑降噪处理，以统计规律为基础，在按时间顺序排列的采样数据中选择一个固定长度的队列，对每一个队列进行如公式所示的算术运算，将其结果作为该次测量的结果，然后进行一次滑动，当下一个数据进入队列尾后，队列的首个数据会被去掉，以此进行反复运算得出滤波结果。

(1)

式中，N为队列长度；x为测量的带噪声数据；Y为降噪后的数据。

2.1.2 SuperSmoother算法

SuperSmoother是Friedman[16]提出的一种数据降噪平滑算法，通过局部线性回归的方法估计若干固定带宽的平滑值，利用固定带宽平滑处理每个初始估计值的留一交叉验证误差，在预测变量范围内的所有数据中挑选初始估计值的最优宽带，用固定带宽取平滑局部带宽，同时从初始估计值中挑两个最优估计值使其带宽最为接近平滑后的带宽，并进行线性插入，插入点再次被固定带宽平滑，最后得到最优平滑结果[17-18]。

2.1.3 小波降噪算法

将实际采集到的信号通过数学表达式可看作真实有效信号和噪声信号的叠加，如所示

S(t)=f(t)+σe(t)，t=0，1…，n-1

(2)

式中，S(t)为含噪声信号，f(t)为真实有效信号，e(t)为噪声信号，σ为噪声程度系数。时域下的真实信号一般是具有连续性的，表现为低频信号；而噪声信号则因为存在较强的随即性质，表现为高频信号，降噪就是利用有效信号和噪声信号在频率上分布不一致去抑制e(t)噪声信号的同时保留真实有效信号f(t)。在降噪的过程中，通过小波分解关系式对含噪信号S(t)进行小波分解，如下所示。

(3)

式中，Ln为低频信息量，Hi为分解第i次的高频信息量。含噪声的信号通过小波变化分解后根据变化后信号的特性对小波系数设置一个阈值，该阈值即是用来处理高频信息量的分界线，对于幅值低于该阈值的高频小波系数将会被去除；而幅值大于该阈值的高频小波系数则会保留，然后对滤除高频信息的信号通过小波逆变换进行信号重构，即可实现信号的降噪[19]。

小波降噪以小波变换为基础，因为小波变换在信号的低频部分具有较高的频率分辨率和较低的时间分辨率，所以小波降噪特别适合用于对非平稳信号进行分析降噪，对于过滤短期高频的异常噪声方面有比较好的效果[20]。小波降噪的降噪过程为：对传感器采集到的含噪数据通过小波变化方法进行信号分解，通过设定阈值的方法消除高频信号数据，其中高频信号数据往往就是原始信号中的噪声部分，最后再通过小波逆变换重构，最终获得降噪处理的数据。小波降噪处理流程如图7所示。

图7 小波降噪过程

图8 不同降噪方法RMSE对比

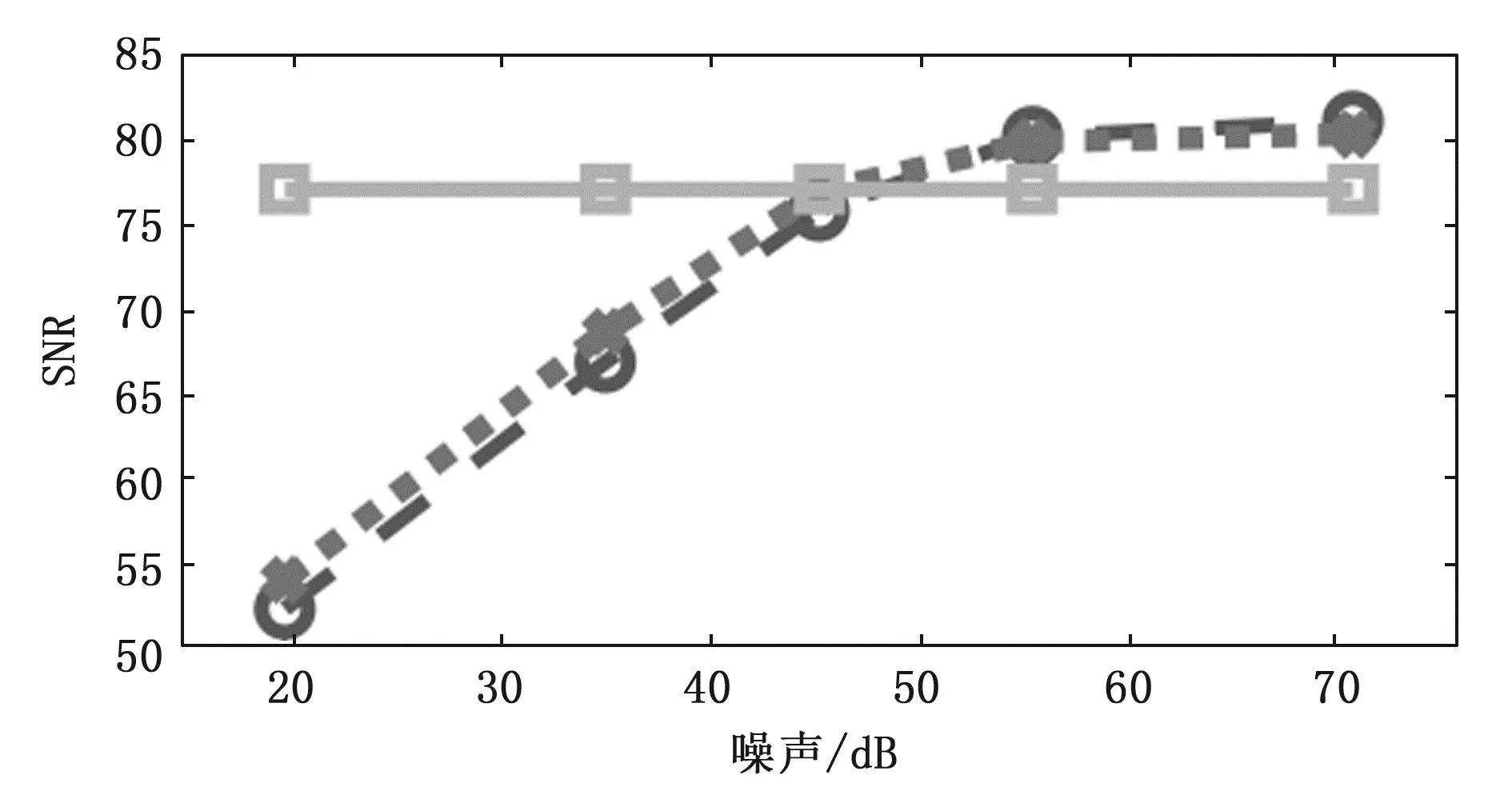
图9 不同降噪方法SNR对比

2.2 数据降噪效果评价指标

数据降噪的评价方法主要是通过对比信噪比SNR和均方根误差(RMSE，root mean squared error)，分别通过以下公式进行计算：

(4)

(5)

式中，x(i)为原始数据；y(i)为降噪后的数据；n为数据个数。信噪比是一种表征信号中噪声含量多少的方法，一般来说，信噪比值越大，则说明降噪效果越好；均方根误差是原始信号与降噪后信号的差异性，一般来说，均方根误差越小，则说明降噪效果越好[21]。本节通过对加噪信号进行降噪处理后的数据与原始数据计算信噪比与均方根误差来判断降噪效果。

2.3 数据降噪效果分析

激光位移传感器是动模在实际试验过程中悬浮高度以及横向位移的测量设备，以下通过激光位移传感器采样频率1 000 Hz为例，通过人工添加20 dB、35 dB、50 dB、55 dB、70 dB的高斯噪声方式模拟正常情况下多种工况对传感器测量的影响。采用3种降噪方法进行降噪处理，结果分别如表3～5所示。

表3 滑动平均降噪结果

表4 小波3层分解降噪结果

表5 SuperSmoother降噪结果

3种降噪方法均能对噪声数据进行有效的降噪，但在不同的信噪比状态下具有不同的降噪效果，SuperSmoother降噪法的降噪效果非常稳定，在20 dB和70 dB的信噪比状态下能够达到几乎相同的降噪效果，表明该算法更适合用于复杂环境下的降噪，在高噪声情况下对数据的降噪效果最佳；尽管SuperSmoother降噪法效果整体较好，但是在信噪比45 dB左右时的降噪效果与滑动平均法和小波降噪法几乎相同，在信噪比达到55 dB时降噪效果甚至略差一些，如下图所示；小波降噪整体优于滑动平均法，但对高信噪比数据进行降噪时的效果相似。在信噪比较低时通过SuperSmoother进行降噪效果较好，信噪比高于达到50 dB选用小波降噪。

2.4 基于降噪差值的数据异常值处理

受到采集与测试系统环境以及传感器自身精度的影响，在传感器数据采集过程中中难免会出现严重偏离实际信息的数据，如果一组由传感器测量组成的数据集合中存在一些严重偏离了该集合中其余大部分数据呈现的变化趋势，则这部分数据就被成为异常值跳点，异常值跳点的出现会严重影响后续对所采集数据的处理与分析，以及相关专业人员对部分数据的研究，因此，为了获得更加可靠的数据，需要对这些异常数据进行剔除。最大值剔除法是最简单的异常值跳点剔除方法，即将整个数据集合中的最大值进行剔除即可。由于系统内各传感器的采集频率较高，通过图像看到异常值而出现跳点时，在其周围也很有可能存在异常值，当该时间段存在多个异常值跳点，如果每次仅剔除一个异常值跳点会浪费大量时间，异常值跳点剔除效率不高。因此可以每次剔除前n个最大值，但由于系统复杂工况可能产生不同运行结果的测量数据，无法精准确定到每种试验工况下该剔除的前n个最大值。阈值判断法是通过人为设定一个阈值，判断某次数据信息与前一个采集点数据信息的差值大小是否超过设定的阈值，该方法同样必须针对不同的传感器以及类型进行阈值的设定，同时，采集与处理系统的采集环境存在多种工况，阈值的选择无法统一确定。多倍标准差剔除法一般被用来处理服从正态分布的数据信息，是一种很有效果的异常值剔除方法，基本原理就是将一组数据集合中的与均值之间偏差超过k倍标准差的数据看作异常值跳点，并对该部分异常值进行剔除，工程实际中最常用的为“3 σ”法则，即k取3时的异常值跳点剔除效果最好。但“3 σ”法则仅适用于数据服从正态分布的情况，对于非正态分布数据采用“3 σ”法则进行数据异常值剔除的效果较差，且容易将变化趋势较大的正常数据剔除。画出原始数据测量值与通过降噪后得到的数据值之间差值的概率密度直方图，如图10所示。

图10 数据差值概率密度分布直方图

降噪后数据差值的概率密度服从正态分布，此时采用“3 σ”法则计算差值数据的均值与标准差σ，将数据差值不在范围内的点看作是异常值[22]。

2.5 异常值处理效果分析

对某次测试中激光位移传感器以1 000 Hz采集的数据为例，给出通过设置置信区间为[0.05，0.95]的区间估计法异常值处理结果，与小波降噪差值处理和SuperSmoother差值处理进行对比，同时对基于小波降噪分别进行了3层和7层小波分解。

数据异常值处理结果如图11所示，区间估计法因为异常值判断比较简单，所以效果不太理想，只剔除了部分异常值跳点；基于7层小波分解的异常值处理效果良好，能够剔除大部分明显的异常值跳点，但由于7层小波分解后数据过于平滑，导致异常值偏离程度较小的数据较多时，这小部分异常值仍在范围内；而小波分解只有3层时，在能有效识别明显的异常值跳点外，偏离程度较小的异常值数据剔除效果仍然比较好，基于SuperSmoother的异常值剔除法效果相同，异常值剔除效果优异。

图11 不同方法异常值处理

数据异常值的剔除应该仅用来剔除对数据整体性有较为明显影响的数据，应该尽量避免剔除过多的数据，使得有效数据被清理，导致错误判断。不同异常值剔除法清理的数据个数如图12所示，区间估计识别异常值的效果较低，所以剔除数据个数少；基于7层小波分解的异常值剔除存在部分偏离较小的异常值无法剔除的情况，因此剔除数据个数较少；基于SuperSmoother的异常值剔除法在保证剔除异常值效果与基于3层小波分解的异常值剔除效果相近的情况下，其剔除数据点的个数也比较少，与基于7层小波分解的异常值剔除法剔除数据个数相同，因此错误判断的情况相对更少，效果最佳。

图12 不同异常值剔除法剔除数据点个数

3 结束语

本文搭建了针对低真空管道磁浮动模系统的数据采集与处理系统，采用了GPS+IEEE1588以太网协议实现了分布式时钟同步网络，完成各采集节点的同步采集；对传感器进行了低真空和电磁场环境测试，发现了真空度变大对激光位移传感器测量值减小的现象，但造成该现象的原因较为复杂，真空度对传感器选用材料以及测量原理可能都存在一定的影响。并对其他多种传感器进行了环境影响测试，为后续低真空管道磁浮交通运输系统的数据采集奠定了一定的基础。

以激光位移传感器为例，针对低真空与磁场环境这种特殊环境下的数据进行了处理，SuperSmoother法在各种信噪比情况下的降噪效果较好且稳定，适用于信噪比降低的情况，在信噪比较高时采用合适的小波分解层数进行降噪的效果最优；基于降噪差值的异常值处理方法良好，且适用于非正态分布的数据，具有工程适用价值。