两级变幅应变疲劳本征损伤耗散寿命预测模型研究1)

李文奇 向 忠 李浩然,2) 任忠凯 王嘉栋

* (浙江理工大学机械工程学院,杭州 310018)

† (太原理工大学机械与运载工程学院,太原 030024)

引言

随着科技进步以及国民经济的发展,人们对机械装备的安全性、耐久性和经济性提出了更高的要求.疲劳裂纹广泛存在于各类工程材料及结构中,对安全性和耐久性产生了严重影响[1].由疲劳破坏导致的金属构件失效约占现代构件失效的50%～90%[2],是工程失效的最主要的原因之一[3],危及机械构件的安全运行.低周疲劳破坏,广泛存在于石油、化工、航天等重要的工程领域[4-5].在这些领域,关键构件一旦发生疲劳失效,后果不堪设想.事实上,构件低周疲劳破坏与其承载历史密切相关[6],如变幅载荷、多轴非比例载荷以及叠加平均应变载荷等.所谓变幅载荷,指的是构件所受载荷谱的特征参数(如应变比、应变幅和平均应变等)处于变化之中.对于实际工程结构件而言,常面临多种服役工况,变幅载荷是其受载的典型特征.基于此,开展变幅低周疲劳寿命预测理论研究,吻合构件受载特征,具有重要的工程应用价值.

变幅低周疲劳载荷,一般由多段不同幅值载荷构成.诸多实验研究表明,不同幅值载荷路径之间的交互作用,使得变幅低周疲劳破坏呈现载荷顺序效应[7],对构件的疲劳寿命产生影响.变幅低周疲劳寿命预测理论,核心问题在于构建描述载荷顺序效应的损伤累积模型.自从19 世纪中叶,德国科学家Wohler阐明了疲劳寿命与交变载荷之间的关系后,人们深入理解了载荷顺序效应对低周疲劳寿命的显著影响,并相应地提出了多种变幅低周疲劳损伤累积模型.从宏观角度看,这些损伤累积模型主要可分为两大类: 线性损伤累积模型和非线性损伤累积模型.线性累积损伤模型基于材料损伤与循环比例的正比关系,通过线性叠加各段损伤,并规定当累积循环比达到1 时,材料便宣告失效,例如Palmgren-Miner 准则[8]和Shamsaei 准则[9].后来,Jiang 等[10]、Wang 等[11]以及Li 等[12]认为线性累积循环比无法刻画变幅加载的顺序效应,提出了损伤与循环比非线性关系模型.以上研究成果,为变幅低周疲劳寿命预测研究奠定了重要基础,但一直不存在一个广泛接受的损伤累积模型.

损伤力学法是一个新兴的研究方法,近年来得到了快速的发展和广泛的认同,被认为具有巨大的发展前景.这种方法结合了唯象学和不可逆热力学理论,推导出损伤演化方程,为构建疲劳寿命预测模型提供了重要的理论支持.从不可逆热力学而言,损伤可视为一不可逆热力学过程,伴随能量耗散,且这一能量耗散不全是材料循环稳态应力应变迟滞洄线包围面积[13].损伤力学,基于不可逆热力学,并结合内变量理论,给出了与损伤构成一一映射的本征损伤耗散描述,为揭示疲劳破坏的热力学本质提供了理论基础.近年来,Ferreira 等[14]、Nie 等[15]和Song 等[16]基于Lemaitre 损伤演化方程,建立了变幅低周疲劳寿命预测模型,预测结果较好.但从本质上来说,他们建立的模型大多数以损伤内变量定义寿命耗竭条件,无法刻画低周疲劳破坏的热力学本质,制约了预测稳定性.

考虑到本征损伤耗散与疲劳损伤构成一一映射,且刻画低周疲劳破坏的热力学本质,因此,以等同本征损伤耗散作为损伤转换条件,构建变幅低周疲劳损伤累积模型,具有明确的物理和力学意义.为此,本文基于连续介质损伤力学和不可逆热力学理论,推导了本征损伤耗散功演化模型D型描述,并以等同本征损伤耗散作为损伤转换条件,构建了一种考虑载荷顺序效应的变幅低周疲劳寿命预测模型并与Manson 模型[17]、Kwofie 模型[18]和Peng 模型[19]进行了对比,为变幅低周疲劳寿命精确预测提供了一种方法.

1 本征损伤耗散低周疲劳损伤累积模型

1.1 本征损伤耗散的金属学意义

众所周知,所有材料均由原子组成,原子有序的排布离不开原子键的维持.材料受载荷作用后,原子键会产生位移,进而产生位错移动.这种原子键−位错滑移机制是造成塑性应变行为的细观原因,但该过程中原子键并不一定会分离.然而,当材料存在微缺陷时,如夹杂,原子键位移将被暂停,进而产生脱键[20]行为,导致疲劳损伤累积.考虑到材料中微缺陷的存在,脱键行为无法避免,使得材料在循环载荷下的疲劳损伤演化不可避免.

弹性模量是材料的宏观力学性能,与原子键能紧密相关.多位学者[21-23]通过实验发现脱键行为将导致弹性模量随疲劳损伤演化而退化.由此可知,宏观尺度上的弹性模量的降低是由微观尺度上的脱键行为导致.同时,脱键行为作为一不可逆过程,必然伴有能量耗散,该能量耗散在损伤力学理论框架下被定义为本征损伤耗散[24].综合所述,本征损伤耗散与疲劳损伤演化一一映射,揭示了疲劳损伤演化的热力学本质.采用本征损伤耗散开展低周疲劳寿命预测,具备提升预测效果的基础条件.

1.2 本征损伤耗散表征模型

疲劳损伤是一个不可逆的热力学过程,伴随着塑性流动和损伤演化,关联着热量产生与流动.对于该过程,根据不可逆热力学理论,受损微元体需满足热力学自洽性,一般包括热力学第一定律和第二定律.热力学第一定律,即能量守恒定律,表述如下[25]

式中,σij是应力张量,是弹性应变张量,是弹性应变率张量,是塑性应变率张量,ρ 是材料密度,是热通量对i(i=x,y,z) 取偏导数,是温度变化率,D是损伤内变量,是损伤内变量变化率,g是Helmholtz 自由能,通常认为自由能与无关.张行等[26]视材料损伤演化为一等温过程,受损材料Helmholtz 自由能表述如下

式中,Sijkl是柔度张量,h是裂纹闭合因子,一般取0.2[20].σ1和 σ3分别是第一主应力和第三主应力.损伤力学中,定义损伤驱动力Y为单位时间所释放的弹性应变能,不考虑材料各向异性,由弹性力学可知损伤驱动力Y为

式中,T,j是温度梯度,是热通量对时间的导数,表示塑性耗散率,Y表示本征损伤耗散率.根据本征损伤耗散率表述形式,本征损伤耗散的增量形式为

式中,dD为损伤内变量的增量,可结合Lemaitre 损伤耗散函数[27]和广义损伤流动法则给出

式中,f∗ 为Lemaitre 损伤耗散函数,p是等效塑性应变,S0,S1为材料常数.针对受单轴低周疲劳载荷,循环本构关系可由Ramberg-Osgood 公式给出,式(6)需改写为

式中,K是循环强度系数,n′是循环应变硬化指数,εp是单轴疲劳载荷下塑性应变.值得注意的是,考虑到在压缩应力作用下的损伤驱动力远低于拉应力作用下的,因此在推导式(6)和式(7)的过程中,并没有考虑压缩应力作用下的损伤累积.此外,考虑低周疲劳中弹性应变幅微小,用塑性应变幅近似代替总应变幅,并结合式(6)和式(7),推导对称拉压应变疲劳载荷下的损伤演化模型N型表述为

式中,DN表示材料循环N次对应的损伤累积,Nf表示恒对称拉压塑性应变幅下材料疲劳寿命.

损伤演化模型,描述了损伤内变量随循环周次演化历程.在此历程,伴随本征损伤耗散累积.本征损伤耗散表征可联合式(5)和式(6)及单轴低周疲劳载荷下循环本构关系Ramberg-Osgood 公式推得

她是悄悄离开的，行李不多，就带走了这几年收藏的几十双鞋。她搬了新的出租房，做着邵南的女友之一，很乖，很听话。

式中,B是缩并材料参数,[2n′(S1+1)+1]−1.由微分理论可知,联合式(8) 和式(10)可将本征损伤耗散演化方程的N型表述改写成D型表述

由式(11)可导出材料循环N次对应的累积本征损伤耗散为

式(12)描述了累积本征损伤耗散与损伤内变量之间的作用规律,此规律亦可通过式(9)并结合一阶近似给出累积本征损伤耗散与循环周次间的近似关系

1.3 变幅低周疲劳寿命预测模型

载荷顺序效应对疲劳寿命影响已在多数学者研究中得以体现[28-29].载荷顺序效应通过改变损伤累积速率对疲劳寿命施加影响.以两级应变疲劳损伤为例(如图1 所示): 由式(9)可知,对于对称常幅应变疲劳而言,损伤与循环寿命比N/Nf关系唯一,与应变幅值无关,损伤−循环寿命比曲线唯一(如图1红线所示).而当高−低应变幅两级加载时(如图1(b)红线所示),较等同常幅应变疲劳损伤增大了第二段损伤累积速率,疲劳寿命降低;反之低−高应变幅两级加载时(如图1(a)红线所示),较等同常幅应变疲劳损伤减小了第2 段损伤累积速率,疲劳寿命提高.变幅疲劳寿命预测常根据某一等效准则,如等损伤准则,将前级循环周次当量折算到后级载荷工况下,以此类推,实现多级变幅疲劳寿命预测向常幅疲劳寿命预测的转变.

图1 两级应变载荷下损伤累积示意图Fig.1 Schematic of damage accumulation under two levels of strain loading

考虑到本征损伤耗散靶向材料疲劳损伤演化,且其临界值界定了材料失效判据,关联原子属性和结构,与载荷顺序无关.基于此,可将前级循环载荷作用下的本征损伤耗散等量换算到后级循环载荷下,推导前后级当量循环周次,以期实现多级向常幅疲劳寿命预测转变.对于两级应变疲劳加载,根据式(13),将第1 级载荷循环N1次所累积的本征损伤耗散等量换算到第2 级载荷工况下,有

式中,Neq,2为一级载荷循环周次当量折算到二级载荷下,Nf2为二级载荷作用下的常幅疲劳寿命,Nf1为一级载荷作用下的常幅疲劳寿命,N1为一级载荷下的循环周次,分别为一级和二级对称应变载荷.由式(14)可将两级变幅疲劳寿命预测转换为第2 级载荷作用下的常幅疲劳寿命预测,而在第2 级载荷作用下材料常幅疲劳寿命必然满足

将式(14)代入式(15)导出两级应变疲劳损伤累积模型为

从式(16)可知,Palmgreen-Miner 损伤累积准则认为两级载荷作用下循环寿命比之和达至1,宣告材料寿命耗竭.而根据多数学者实验研究表明,载荷顺序对两级载荷作用下循环寿命比之和施加影响.以300 CVN 合金钢[30]和纤维材料CFR PEEK[31]为例(如图2 所示),Palmgreen-Miner 损伤累积直线恰将两级变幅疲劳实验数据分为了两类(高低加载和低高加载).当高低加载时,Palmgreen-Miner 损伤累积量即循环寿命比之和大于1,而当低高加载时,循环寿命比之和又小于1,Palmgreen-Miner 损伤累积量与载荷顺序密切相关.新建损伤累积模型,描述载荷顺序效应,可由式(16)给出Palmgreen-Miner 损伤累积量的两种载荷情形

图2 两级载荷作用下循环寿命比之和与载荷顺序关联Fig.2 Sum of cycle life ratios under two levels of loading as a function of loading sequence

由式(18)可知,新建损伤累积模型描述载荷顺序效应,吻合现有考虑载荷顺序效应的实验规律.实际上,在预测两级变幅疲劳寿命的过程中,主要依赖于损伤累积模型来估算第2 级载荷作用下的剩余寿命.然后,将这个剩余寿命与第1 级载荷作用下已消耗的寿命相加,以此获得完整的预测寿命.基于该预测思路,并结合式(16),给出两级应变疲劳载荷作用下材料预测全寿命为

预测模型计算流程如图3 所示.

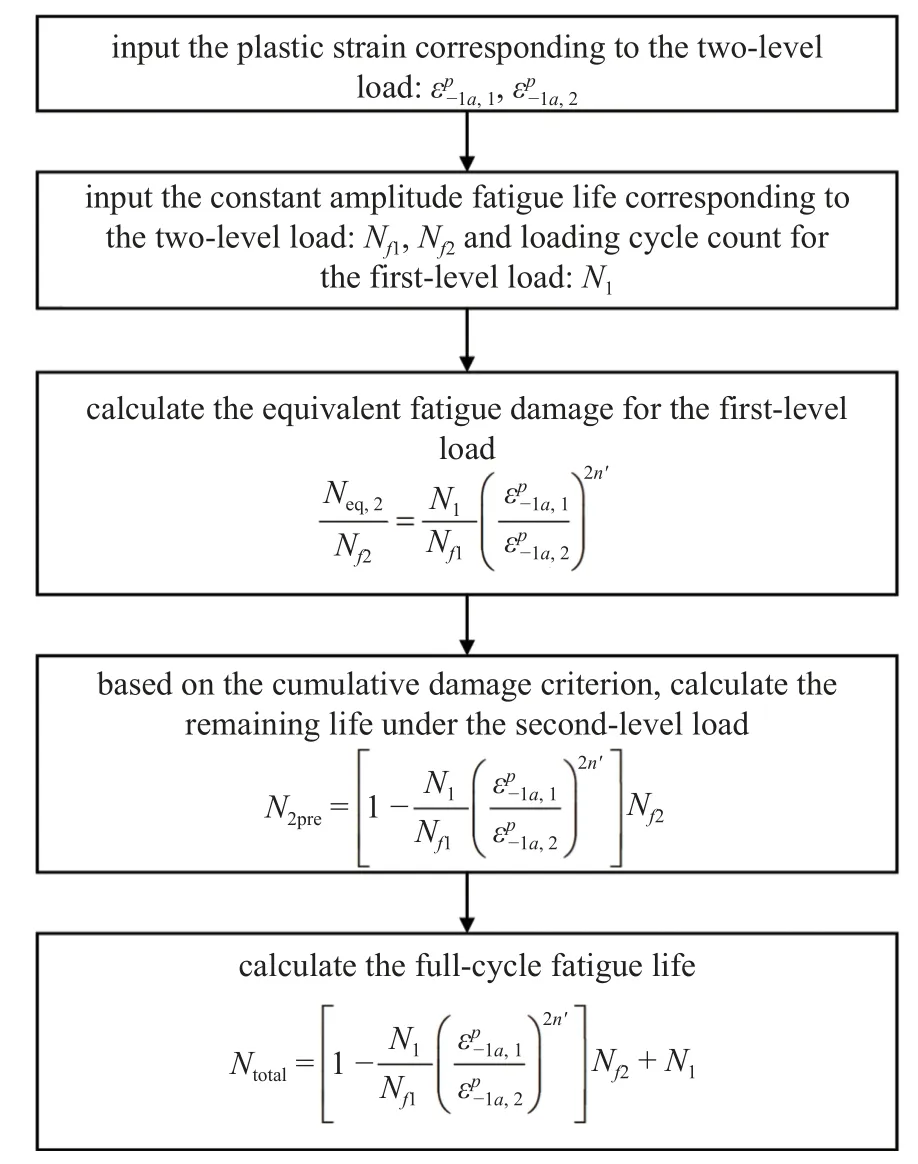
图3 变幅低周疲劳寿命预测模型计算流程图Fig.3 Calculation flowchart of variable amplitude low circumference fatigue life prediction model

2 模型验证

为进一步对比验证新建变幅应变疲劳寿命预测模型先进性,本文收集两种金属材料P355NL1 结构钢[32]和Ti-6Al-4V 钛合金[33-34]在两级变幅对称应变疲劳载荷下的实验数据开展了对比验证,其中对比预测模型包括考虑载荷顺序效应的Manson 模型、Kwofie 模型和Peng 模型.两种实验材料疲劳性能属性及实验应变载荷下常幅中值疲劳寿命分别如表1 和表2 所示.P355NL1 钢和Ti-6Al-4V 钛合金低周疲劳实验均通过制备光滑试样在应变载荷控制模式下进行,具体载荷工况如表3 所示.

表1 两种材料的疲劳性能参数Table 1 Fatigue performance parameters of the two materials

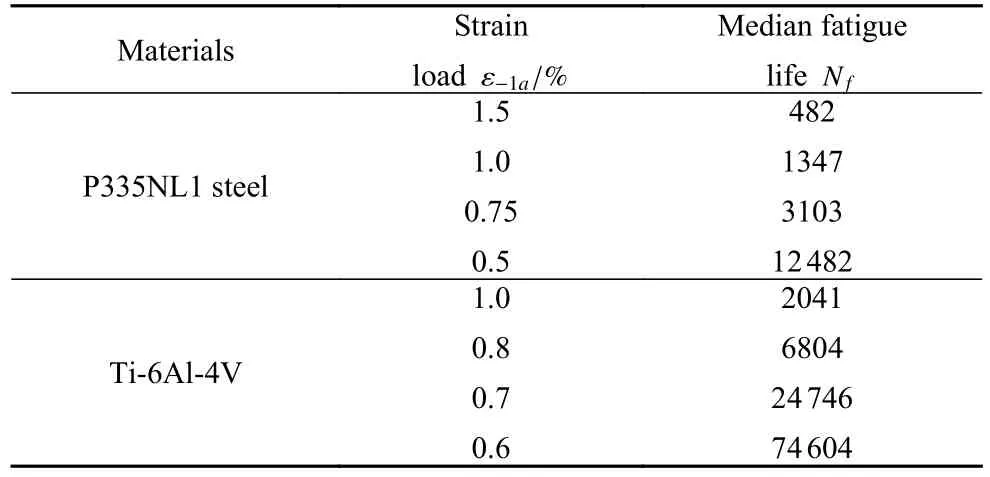
表2 两种材料在应变载荷下常幅疲劳寿命Table 2 Experimental strain loaded normal amplitude fatigue life for both materials

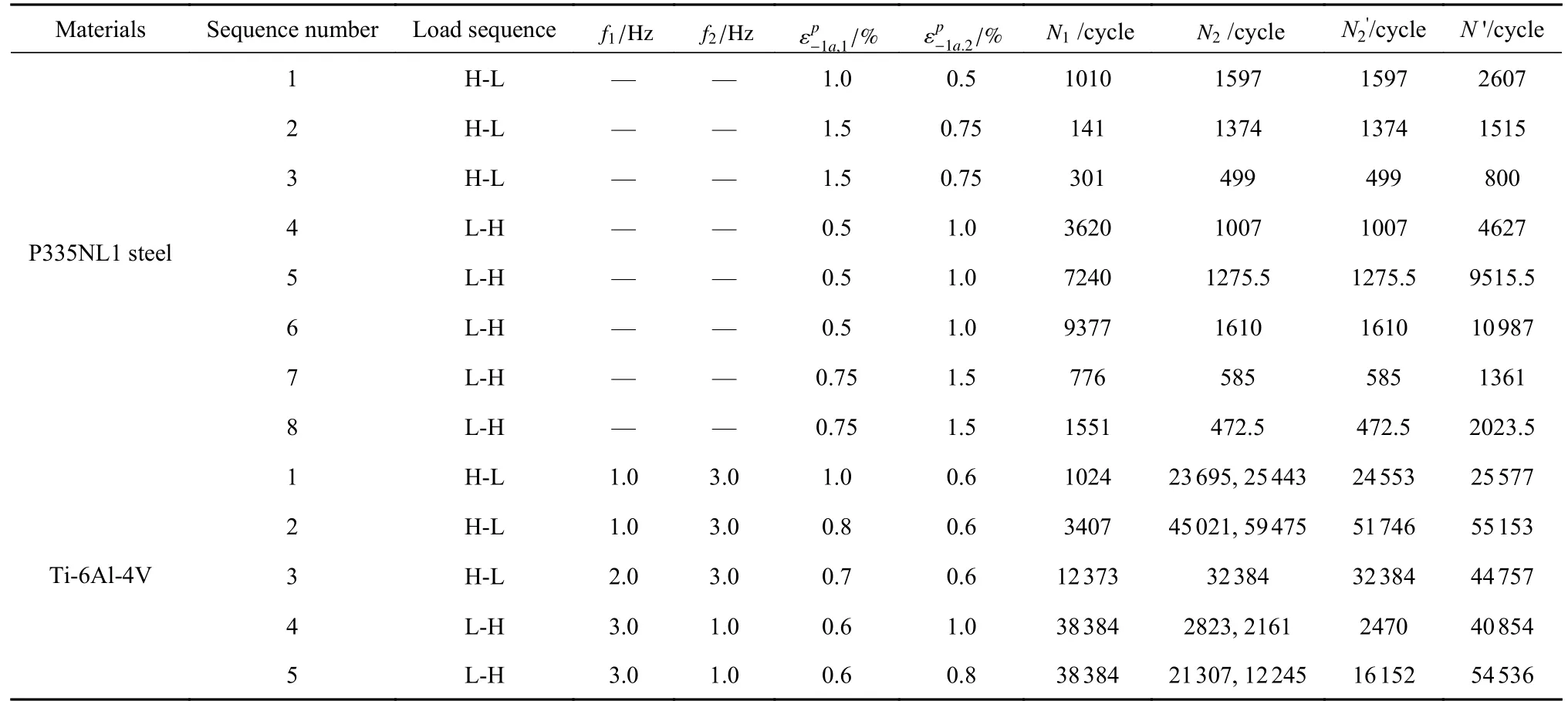
表3 两种材料的具体实验载荷工况Table 3 Specific experimental loading conditions for both materials

新建模型、Manson 模型、Kwofie 模型和Peng 模型对两种材料的预测结果如图4 和图5 所示,图中两条蓝色实线组成1.5 倍公差带.从图中可以观察到,本研究构建的疲劳寿命预测模型对于两种金属材料在单轴两级变幅载荷下的疲劳寿命预测与实验结果具有良好的一致性,所有数据点都在1.5 倍误差范围内.相比之下,Manson 模型、Kwofie模型和Peng 模型的预测结果都存在部分数据点超出了1.5 倍的误差带.预测结果表明,对于单轴两级变幅载荷下疲劳寿命的预测,新建模型预测效果最优.此外,新建模型、Manson 模型、Kwofie 模型和Peng 模型对P355NL1 结构钢预测结果数据点分别有5/8,6/8,5/8 和4/8 落入虚线右侧,对Ti-6Al-4V钛合金预测结果数据点分别有3/5,5/5,4/5 和4/5 落入虚线右侧.预测结果数据点相对虚线位置表明,新建模型、Manson 模型、Kwofie 模型和Peng 模型的预测结果均偏保守估计.

图4 P355NL1 结构钢预测结果误差分散图Fig.4 Dispersion graph of prediction errors for P355NL1 structural steel

图5 Ti-6-Al-4V 钛合金模型预测误差分散图Fig.5 Dispersion of model prediction errors for Ti-6-Al-4V titanium alloy

3 结论

(1) 基于连续介质损伤力学及其不可逆热力学框架,以本征损伤耗散功法开展变幅载荷下的低周疲劳寿命预测,具有明确的物理和力学意义.

(2) 通过对P355NL1 结构钢和Ti-6Al-4V 钛合金的两级变幅低周疲劳寿命预测结果表明,新模型的预测结果与试验结果较为吻合,且优于Manson 模型、Kwofie 模型和Peng 模型.

(3) 由于本文所建的变幅寿命预测模型针对的载荷工况为对称应变循环载荷,对于其他载荷工况,需要利用相应的应变等效准则实施寿命评估,但其评估效果需要进一步研究.

(4) 本文模型依据等效损伤的思想,借助本征耗散模型将两级变幅应变载荷中第1 级载荷损伤等效到第2 级载荷损伤,从而建立疲劳寿命预测模型.使用该方法可以将两级变幅应变疲劳推广到多级变幅应变疲劳,以建立多级变幅应变疲劳下疲劳寿命预测模型,但此项内容尚需进一步探究与论证.

(5) 由于材料在应力控制和应变控制下低周疲劳失效的主要原因不同,本文所提出的预测模型是基于应变控制下低周疲劳失效,该模型在应力控制下低周疲劳寿命预测是否准确,其评估效果待进一步研究.