可压缩边界层的入口合成湍流生成方法1)

王 天 孙 东 郭启龙 李 辰 袁先旭 李 博

* (中国空气动力研究与发展中心,空天飞行空气动力科学与技术全国重点实验室,四川绵阳 621000)

引言

湍流边界层在航空航天工程中普遍存在,对飞行器的气动特性有重要影响,因此实现对湍流边界层的准确模拟具有迫切的实际需求.湍流数值模拟方法主要包括[1]直接数值模拟(direct numerical simulation,DNS)、大涡模拟(large eddy simulation,LES) 和雷诺平均Navier-Stokes 方程(Reynolds averaged Navier-Stokes,RANS)模拟.DNS 能够解析流场中的全部尺度,常被用于机理分析,但其对计算资源要求较高,无法应用于高雷诺数复杂外形中的工程计算.LES 计算量较DNS 更小且能够解析流场中的精细流动结构,但在近壁区域的网格需求仍十分巨大,无法满足当前的工程应用.RANS 方法通过对雷诺平均方程未封闭项进行建模大大降低计算量,广泛应用于当前的工程计算当中.但RANS 方法无法准确模拟大分离流动,也无法获得精细的非定常流动特征.

过去20 年来,融合了LES 与RANS 优势的混合RANS-LES 方法[2-4](hybrid RANS-LES method,HRLM)为发展满足工程需求的湍流模拟手段提供了新思路[5].根据RANS 和LES 混合方式可分为分区混合方法和非分区混合方法.在分区混合方法中,需要人为确定交界面,并在两侧分别使用RANS 和LES.从RANS 向LES 的过渡过程中,由于缺少LES 所需的湍流脉动,流场中会产生一段适应区域使流场恢复至真实湍流.为缩短此区域范围并节省计算资源,在交界面上添加合理的非定常脉动是十分必要的.

针对如何添加合理的湍流脉动这一问题,Tabor等[6]、Wu[7]和Dhamankar 等[8]针对这方面的研究进展做了全面详尽的综述.入口处的脉动生成方法被分为3 大类: 预先模拟类(precursor simulation)、回收调节类(recyling-rescaling method,RRM)、合成湍流法(synthetic turbulence,ST).3 类方法各有优缺点及其适用场合.从工程应用的角度来看,ST 类方法具有两方面优势: 一是其计算代价相对较小;二是其所需的输入信息常规RANS 方法均可提供.因此ST 类方法得到了广泛的关注.

ST 类方法本质上是从湍流的低阶统计信息中重构高阶统计信息,可以通过多种途径实现.其中合成湍流生成器[9-11](synthetic turbulence generator,STG)、合成涡方法[12-13](synthetic eddy method,SEM) 和数字滤波法[14-15](digital filter method,DFM)是3 种应用较多的方式.这些方法的性能主要依赖于输入的湍流低阶统计量,如湍动能和长度尺度,其中长度尺度具有较大的不确定性,不同RANS 模型给出的近似分布可能存在明显差别,Guo 等[11]讨论了不同长度尺度分布对ST 性能的影响,并给出了一种基于一方程S-A 模型的长度尺度构造方式.另一方面,上述ST 方法添加的湍流脉动一般仅含速度脉动,在可压缩边界层中,除了包含速度脉动,还包含温度、密度、压力等热力学变量的脉动.在高马赫数湍流边界层的HRLM 模拟中,也可以忽略热力学量脉动,直接使用ST 方法在入口/交界面上添加速度脉动,但可能会降低合成边界层脉动恢复到物理真实脉动的速度.对于如何在湍流入口中添加热力学脉动这一问题,Martin[16]在开展可压缩壁湍流直接数值模拟的过程中,基于强雷诺比拟(strong reynolds analogy,SRA)给出了流场初始的温度脉动及密度脉动.SRA 是Morkovin[17]在研究可压缩湍流中提出的直接反映速度脉动和热力学量脉动之间关系的理论.此理论使得湍流入口的热力学脉动量可直接由速度脉动得到.Adler 等[18]结合DFM 和SRA 给出了湍流入口的速度脉动和热力学脉动.但是原始SRA 关系式被证明并不严格成立[19-20],Gaviglio[21]和Huang 等[22]提出了新的改进的SRA关系式.这些关系式均可用来构建入口的热力学脉动.

本文主要开展两方面工作: 一是在不可压缩和可压缩的典型壁湍流算例(槽道湍流和边界层湍流)中,对比分析STG,SEM 和DFM 3 种合成湍流方法作为湍流入口对流场发展过程的影响;二是针对可压缩壁湍流的模拟,探讨了若干强雷诺比拟方法所得到的热力学量脉动对流场发展的影响.

1 合成湍流入口方法及计算模型简介

合成湍流方法通过局部的平均量和湍流统计特征量构建湍流脉动,操作简单,被广泛应用于湍流入口.

速度ui(r,t) 可以被分解为时间平均速度(r) 和脉动速度(r,t),如式(1)所示,r为位置矢量.合成湍流的目的是构建合理的脉动速度

在湍流边界层中脉动速度具有各向异性,Davidson[23]提出了通过求解雷诺应力张量的特征值实现各向异性的方法,对雷诺应力张量R进行Cholesky 分解,即R=ATA

各向异性脉动速度通过如下方式获得

1.1 合成湍流生成器

本文采用的STG 方法为文献[11]中提出.首先通过一系列时空Fourier 模态加权叠加得到辅助矢量

其中上标“n”表示第n个模态的参数,q是归一化幅值,由RANS 结果计算得到,kn=kn·dn为三维的波数矢量,kn表示波数矢量的模,dn为均匀分布于单位半径的球面上的随机方向矢量,σn为随机生成的、与dn垂直的单位矢量,φn是均匀分布于[0,2π]区间的随机相位.所有以上这些随机量随n变化,且在计算过程中不随时间变化.具体细节及构造方法详情可参见文献[10].

1.2 数字滤波法

数字滤波法最早由Klein 等[24]提出,此方法利用滤波的数学性质,设计满足在随机波动中建立高斯两点相关函数的数字滤波器,构建满足所需长度尺度的随机速度分布.之后Xie 等[25]采用二维滤波改进了原始的方法,大大节省了计算资源.Adler 等[18]提出了一种改进的数字滤波法能够满足复杂外形.本文采用文献[18]给出的构造方式,其速度脉动采用式(3)构建,辅助矢量的构建方法如下

式中 ηl(j,k) 为定义在入口或交界面平面上的滤波随机向量,(j,k) 表示平面上的网格计算坐标,It为积分时间尺度.

式中,下标0 为选定的流场位置,式(6)即以选定位置为中心进行滤波,α 为归一化常数,Ij和Ik为各方向上的积分长度尺度,r为随 (j,k) 均匀分布的随机数序列.

1.3 合成涡方法

Jarrin 等[12]通过在入口平面引入人工涡的方法建立速度脉动场,每个涡由特定形状函数表示,描述其空间和时间特征.本文采用文献[13]中速度脉动构建方法

其中,VB为旋涡所占体积,σ 为模型的长度尺度,由RANS 结果得到.其他具体参数可参见文献[13].

1.4 数值方法和模型

本文对可压缩Navier-Stokes 方程进行求解,采用基于S-A 模型的IDDES 进行模拟,详情见文献[26].其中无黏项采用文献[27]中的hyWENOUW4 格式,黏性项离散使用4 阶中心差分格式,时间推进采用隐式双时间步法.本文算例中均在入口添加人工合成湍流脉动.

2 合成湍流入口条件对比分析

本节分别采用STG,DFM 和SEM 方法生成湍流脉动应用于不可压缩槽道湍流和可压缩壁湍流的入口条件中,对比分析了其对流场壁面摩阻、流场结构、雷诺应力等随流场发展的影响.

2.1 对不可压缩槽道湍流发展影响

槽道湍流被广泛用于对湍流入口条件的生成方法进行测试[10,28-29].本节分别使用STG,SEM 和DFM 方法在入口添加湍流速度脉动对充分发展槽道湍流进行模拟.来流马赫数为0.2,基于槽道半宽h和壁面摩擦速度uτ的雷诺数Reτ=395,计算域范围为x×y×z=32.5h×2h×3.4h.流向(x方向)、法向(y方向)和展向(z方向)网格数分别为Nx×Ny×Nz=469×109×139,其中第1 层网格高度ymin=0.02h,流向网格和展向网格均匀分布Δx=0.07h,Δz=0.025h,对应的≈0.79,Δx+≈27.65,Δz+≈9.875.槽道展向采用周期性边界条件,壁面法向边界采用等温无滑移条件.

图1 展示了入口截面(x/h=0)上3 种合成湍流方法下入口的展向脉动速度云图.STG 和DFM 均添加了大量的脉动区域,区域范围沿壁面法向逐渐变大;在接近壁面处,DFM 添加的脉动范围呈现法向短展向长的细长形;而SEM 添加的脉动数量较少,且在相同法向距离下脉动尺度明显大于STG 和DFM.

图1 入口处展向速度云图Fig.1 Spanwise velocity contour of inflow

通常采用时均摩阻沿流向的变化来反映入口合成湍流的品质,定义恢复距离为时均摩阻完全恢复至参考值5% 以内的位置距入口的流向长度.图2展示了STG,DFM 和SEM 3 种合成湍流入口条件下时均摩阻分布.RANS 能够准确模拟此构型的流场[30],因此图中以RANS 模型计算结果作为参考值.对比结果表明,在添加合成湍流后,摩阻均在入口附近的一段区域内明显低于参考值.其中,DFM 和SEM 两种方法得到的恢复距离约为15h,STG 得到的恢复距离约为7h,优于其他两种方法.

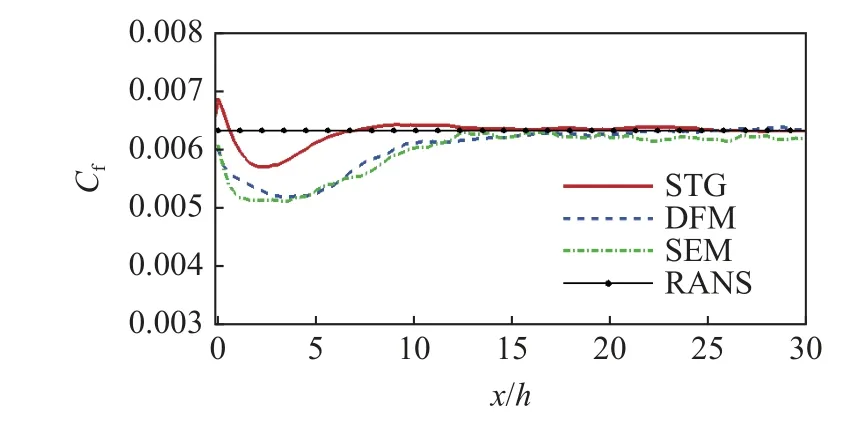
图2 不同合成湍流入口下摩阻对比Fig.2 Comparison of frictions of different inlet boundary conditions

图3 给出了不同合成湍流入口条件下半槽道流场的瞬时Q等值面(Q=0.05),用于显示旋涡结构,等值面采用流向速度着色.结果显示,STG 方法和DFM 方法添加湍流脉动后,入口后出现类似的大尺度流向相干结构,其中DFM 流场中此结构区域较大,导致恢复距离明显长于STG.SEM 添加湍流脉动后无大尺度流向相干结构.图4 给出了y/h=0.2位置x-z截面的涡量云图.对比STG 和DFM 的结果,在流场入口后均存在大尺度结构,但STG 的恢复距离明显更短.SEM 下流场结构随流向变化并不明显.

图3 流向速度着色的Q 等值面(Q=0.05)Fig.3 Isosurfaces of the Q-criterion coloured by streamwise velocity(Q=0.05)

图4 槽道y/h=0.2 横截面涡量云图Fig.4 Contours of vorticity,over the x-z plane at y/h=0.2 in channel flow

为定量描述流动的发展过程,图5～图7 给出了3 种湍流入口下流向x/h=0,3,6,12,20 位置处的基于摩擦速度的雷诺应力.其中选择周期边界条件的IDDES 结果及Poletto 等[31]计算结果代表完全发展湍流值作为参考.图5 展示了R12随流向的发展过程,可以发现,STG 方法下切应力向参考值恢复得更快.其中在x/h=6 处,STG 下已基本恢复,而DFM 和SEM 下的值仍与参考值相差较大.在x/h=12 后,各方法下R12已基本恢复至参考值,但继续随流向发展DFM 下R12与参考值仍有一定差异.对比图6 中R11发展过程,STG 及SEM 下均能迅速恢复至参考值,而DFM 下恢复速度较慢,在x/h=12 后才逐渐与参考值靠近.对于图7 中R22发展变化曲线,3 种入口条件下恢复均较慢,在x/h=12处数值均与参考值有一定差距.

图5 不同合成湍流入口下 R12 随流向变化Fig.5 R12 development along streamwise using different inlet conditions

图6 不同合成湍流入口下 R11 随流向变化Fig.6 R11 development along streamwise using different inlet conditions

图7 不同合成湍流入口下 R22 随流向变化Fig.7 R22 development along streamwise using different inlet conditions

2.2 对可压缩壁湍流发展影响

针对可压缩算例,本节选择Ma=2.5 零压力梯度平板算例开展研究,流向(x方向)、法向(y方向) 和展向(z方向) 网格数为Nx×Ny×Nz=374×121×59,其中法向第1 层网格≈0.38,流向网格和展向网格均匀分布 Δx+≈24,Δz+≈13,出口处网格稀疏处理,使用海绵层[32]来消除出口边界的虚假反射波.表1 中 θ 为入口动量厚度.

表1 来流条件Table 1 Inlet conditions

图8 展示了超声速平板入口的展向速度脉动,δ0为入口边界层厚度.可以直观地观察不同合成湍流方法在入口处添加的脉动.可以发现,STG 和DFM 流场中接近壁面处均存在多个小范围速度脉动区,DFM 中湍流脉动区域更多呈现展向细长状,且尺度较小集中于壁面附近.SEM 方法添加湍流脉动后,入口处存在数个大范围速度脉动.

图9 展示了STG,DFM 和SEM 3 种方法下壁面摩阻沿流向的发展曲线,其中选择Van Driest[33]的经验公式作为对比.图中,STG 和SEM 下摩阻发展趋势基本一致,恢复距离约为 10δ0,而DFM 摩阻一直偏低,且恢复缓慢,发展至x/δ0=20 处仍有一些差距.总的来说,Ma=2.5 超声速平板流中STG 和SEM 入口条件下恢复距离相比较短,DFM 恢复距离最长且精度最差.

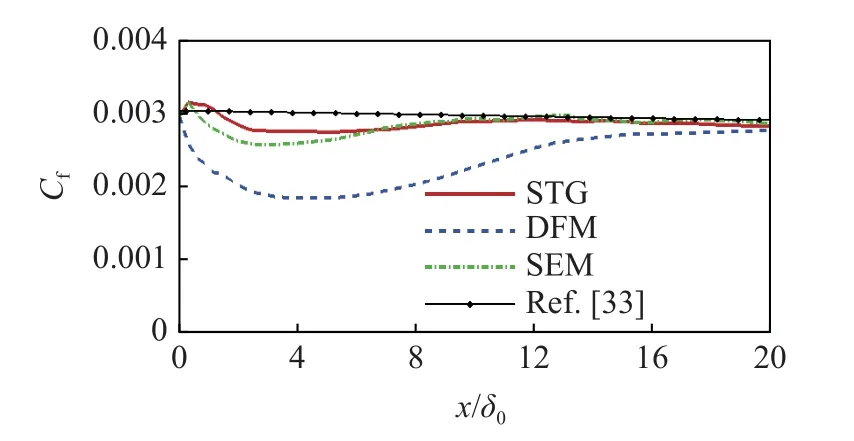
图9 不同合成湍流入口摩阻对比Fig.9 Comparison of frictions of different inlet boundary conditions

图10 展示了边界层内流场的Q等值图(Q=0.2),其中采用流向速度着色.图中观察到STG 与DFM流场发展过程相似,入口处存在流向相干结构,但STG中此结构明显短于DFM 中.SEM 下流场逐渐由小尺度结构发展为较大尺度的湍流结构.图11 给出了y/δ0=0.2横截面的涡量云图,与上面描述基本一致.

图10 边界层内Q 值等值面(Q=0.2)Fig.10 Isosurfaces of the Q-criterion in boundary layer (Q=0.2)

图11 湍流边界层 y/δ0=0.2 横截面涡量云图Fig.11 Contours of vorticity,over the x-z plane at y/δ0=0.2 in turbulent boundary layer

本节分别选择流向x/δ0=0,3,6,12,20 位置来对比不同合成湍流方法下基于黏性尺度的雷诺应力随流向的发展变化过程,如图12～图14 所示.其中选择Pirozzoli 等[34]的DNS 结果作为参考.对于而言,SEM 入口条件下迅速恢复至参考值附近,STG 中流场不同流向位置处曲线变化并不大,但与参考值有一定差距,而DFM曲线随流向变化剧烈且误差更大;随流向变化中可以发现,STG 和SEM 下曲线可迅速恢复至参考值,且SEM 精度更高;而随流向变化图中STG方法下精度最高.

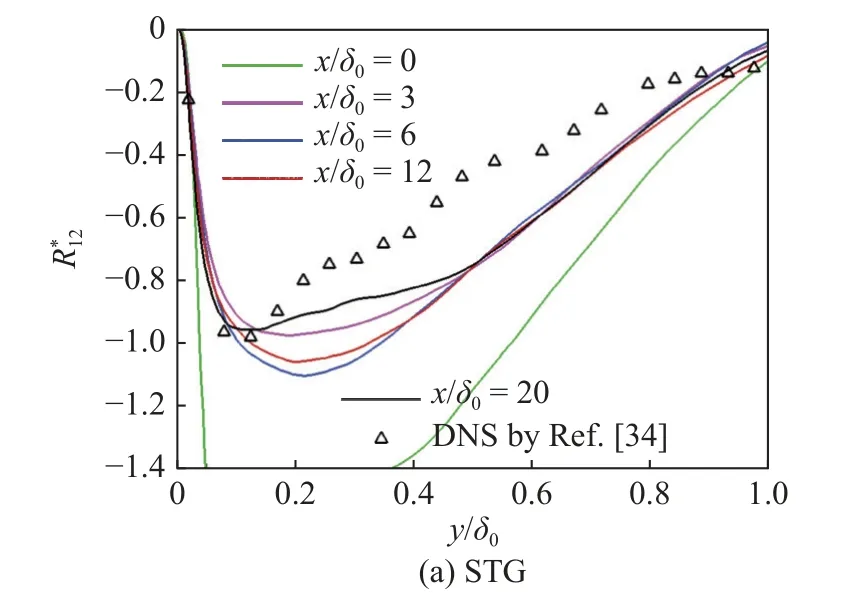
图12 不同合成湍流入口下 随流向变化Fig.12 development along streamwise using different inlet conditions

图13 不同合成湍流入口下 随流向变化Fig.13 development along streamwise using different inlet conditions

3 添加热力学脉动入口条件对比分析

本节选择Ma=2.5,5.0 工况下开展入口添加热力学脉动对流场发展影响研究.其中Ma=2.5 计算条件与2.2 节中相同.在Ma=5.0 算例中,流向(x方向)、法向(y方向) 和展向(z方向) 网格数为Nx×Ny×Nz=336×181×69,其中法向第1 层网格≈0.46,流向网格和展向网格均匀分布 Δx+≈36.8,Δz+≈18.4.来流条件如表2 所示.

表2 来流条件Table 2 Inlet conditions

3.1 热力学脉动添加方法

使用式(3)仅能给出速度脉动,但对于高马赫数边界层,热力学量的脉动也是不可忽略的一部分.通常的做法是使用各种强雷诺比拟(strong Reynolds analogy,SRA)来给定温度脉动的均方根值.在绝热壁面条件下,温度脉动的均方根可以表示为

式中T表示温度,“～”表示Favre 平均量.但是对于等温壁面,式(11)给出的统计结果并不完全正确,又有学者提出了修正的雷诺比拟[35],其统一形式可以写为

本文所采用的原始强雷诺比拟以及Gaviglio[21]和Huang 等[22]修正后的参数a和c的取值参见表3,分别称为SRA,GSRA 和HSRA.其中HSRA中c=Prt,如下式所示.但在入口处Prt需要取定值,Zhang 等[35]提到Prt参考值为 0.7 ∼0.9.本文为使GSRA 及HSRA 添加热力学脉动入口条件后流场发展过程对比明显,在入口中取Prt为0.7.

表3 入口条件中强雷诺比拟系数表Table 3 SRA’s coefficients of inlet conditions

在由式(12)得到温度脉动后,通过完全气体状态公式和零压力脉动假设可以得到密度脉动,如下式所示

3.2 入口添加热力学脉动对流场发展影响

综合第2 节中的对比结果,STG 相对其他方法表现出一定的优势.因此为对比可压缩条件下不同热力学脉动生成方法对流场发展的影响,本文采用STG 方法添加速度脉动,并通过不同强雷诺比拟在入口处添加热力学脉动.本节分别模拟了Ma=2.5和Ma=5.0 条件下的湍流边界层,后续采用“case 0”代表入口处不添加热力学脉动,分别采用“case 1”,“case 2”和“case3”代表采用SRA,GSRA 和HSRA 添加热力学脉动.图15 给出了不同马赫数下得到的摩阻分布.从摩阻分布中发现,不同热力学脉动入口条件下恢复距离基本一致.图16 给出了完全湍流区内基于黏性尺度的雷诺应力数值不同入口条件下结果差距较小,且均能取得合理的结果.

图15 不同入口条件下摩阻曲线Fig.15 Comparison of frictions of different inlet boundary conditions

图16 边界层模拟得到的完全湍流区后的雷诺应力Fig.16 Reynolds stresses in fully-developed turbulence

下面将分析SRA,GSRA 和HSRA 添加热力学脉动后的入口条件对流场发展的影响.式(13)中湍流Prandtl 数表征平均运动中动量交换和热交换之比,在强雷诺比拟中此值近似为1.图17 展示了Ma=2.5,5.0 下完全湍流区内不同入口条件下湍流Prandtl数沿法向的分布,其中线点图表示Ma=2.5 条件,DNS 结果取自文献[36].可以发现,在完全湍流区内,采用不同强雷诺比拟添加热力学脉动作为入口条件后,湍流Prandtl 数变化趋势基本一致,其数值沿法向从1 逐渐下降至0.7 附近,与Pirozzoli 等[37]和Duan 等[38]的结果也基本一致,证明了本文对于流场热力学量模拟的准确性.

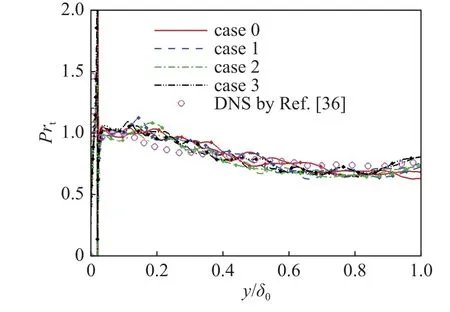
图17 完全湍流区内湍流Prandtl 数法向分布Fig.17 Turbulent Prandtl number in fully-developed turbulence

在不同流动条件下(槽道和边界层),不同壁温条件下有大量DNS 数据[37-41]表明HSRA 相比于SRA 和GSRA 表现更好.Guarini 等[41]深入分析了HSRA 关系,指出HSRA 有效意味着湍流场中法向方向的动量和热量输运具有相似性.因此本文定义由HSRA 定义的公式来衡量流场热力学量的发展过程

图18 展示了两种马赫数下完全湍流区内f的数值,其中线点图代表Ma=2.5.不同入口条件下不同马赫数下曲线基本一致.在完全湍流区处f值在边界层内沿法向逐渐降低至1 附近.

图18 完全湍流区内 f 分布Fig.18 f distribution in fully-developed turbulence

图19 给出了Ma=2.5,5.0 下x/δ0=2,6,10,14位置处的f的数值,其中线点图代表Ma=2.5.随流向发展,不同入口条件下f逐渐靠拢至1 附近.可以对比观察到图中case 0 曲线向完全湍流数值恢复得最慢,即在流场入口处不添加热力学脉动后流场中热力学量向完全湍流状态恢复得更慢.在不同位置处,可以明显观察到case 2 和case 3 入口条件下流场热力学量恢复得更快.在x/δ0=2,4 两个位置处可以发现case 2 中恢复速度最快.因此采用GSRA,HSRA 在入口处添加热力学脉动均能加快流场中热力学量的恢复速度,且GSRA 效果稍好于HSRA.

图19 Ma=2.5,5.0 下不同流向位置fFig.19 f distribution in various streamwise position of Ma=2.5,5.0

3 结论

本文分别以STG,DFM 和SEM 3 种方法添加入口湍流脉动开展了低马赫数槽道湍流和超声速湍流边界层的数值模拟研究,通过对比分析流场中的湍流脉动、壁面摩阻、流场结构、雷诺应力和热力学量等信息后,得到以下结论.

(1) 在不可压缩和可压缩(不添加热力学量脉动)壁湍流问题模拟中,STG,DFM 和SEM 方法均能获得充分发展的湍流结构.对比发现,在不可压槽道湍流中,STG 能够最快获得合理的摩阻分布,流场结构与雷诺应力发展也有一定的优势;在可压缩湍流中,STG 与SEM 表现相近,均优于DFM 方法.

(2) 在马赫数2.5 和5 下分别在入口处通过SRA,GSRA 和HSRA 添加热力学脉动开展湍流边界层数值模拟研究.结果显示,是否添加热力学脉动对于摩阻和雷诺应力发展影响较小,但对流场中的热力学量有很大的影响.其中通过GSRA 添加热力学脉动后流场热力学量恢复最快.